罕遇地震作用下高墩大跨连续刚构桥地震响应分析

谭冠生（中铁第四勘察设计院集团有限公司，湖北武汉　430063）



罕遇地震作用下高墩大跨连续刚构桥地震响应分析

谭冠生
（中铁第四勘察设计院集团有限公司，湖北武汉430063）

摘要建立基于纤维模型有限元法的非线性数值分析模型，研究某高墩大跨连续刚构桥在罕遇地震作用下的动力响应。首先，对桥梁动力特性进行分析。然后，将顺桥向和横桥向罕遇地震作用下采用线性与非线性动力时程分析法计算的地震响应结果加以对比，发现各墩墩顶线性与非线性位移响应基本相同，而墩顶与墩底的线性、非线性内力响应差异较大，表明结构在罕遇地震作用下进入非线性阶段，线性时程计算结果无法真实反映桥梁响应情况。最后，采用非线性动力时程分析法进一步研究罕遇地震作用下墩高对桥梁抗震性能的影响，结果表明:在顺桥向罕遇地震作用下，墩底弯矩达到最大时高墩最大转角远小于矮墩，矮墩易进入塑性阶段；在横桥向罕遇地震作用下，墩底弯矩达到最大时矮墩最大转角远小于高墩，高墩易进入塑性阶段。

关键词连续刚构桥；罕遇地震；纤维模型；有限元法；时程分析

在我国西部地区交通建设中，整体性能好、跨越能力强的高墩大跨连续刚构桥得到快速发展。这些桥梁地处高烈度区，应考虑其在高强度地震作用下的抗震性能，保证其满足“小震不坏，中震可修，大震不倒”的抗震设计原则［1］。我国学者对高墩大跨连续刚构桥在地震作用下响应的研究，多是在多遇地震作用下的弹性计算。文献［2］通过对5座连续刚构桥进行地震响应分析得出，地震波输入的方向不同，对高墩与矮墩的影响则不同，并指出地震作用下的控制断面在桥墩墩底、主梁跨中和根部。文献［3］分别对连续刚构组合桥与连续刚构桥进行了反应谱和线弹性动力时程分析。文献［4-5］对连续刚构桥进行了线性时程分析，计算了不同波速下其地震响应，讨论了行波效应对连续刚构桥地震响应的影响。对于在罕遇地震作用下、采用非线性动力时程分析方法、考虑材料非线性后桥梁结构的地震响应研究则较少。

本文以某6跨高墩大跨连续刚构桥为研究对象，建立基于纤维模型有限元法的非线性数值分析模型，对顺桥向和横桥向罕遇地震作用下采用线性与非线性动力时程分析法计算的地震响应结果进行对比分析。在此基础上，采用非线性动力时程分析法进一步研究墩高对罕遇地震作用下桥梁抗震性能的影响，为高墩大跨连续刚构桥抗震设计提供参考。

1　模型的建立

纤维模型［6］通常将杆件划分为多个单元，然后将单元离散成若干截面，通过插值函数将单元节点与截面的关系建立起来，最后再把截面离散成一定数量的纤维，通过平截面假定得到截面和纤维的变形关系。纤维模型中的纤维可采用材料单轴本构关系，避免了其他模型中难以给定的多维本构关系问题。其简洁明确的物理概念以及可靠的分析结果，使其在结构弹塑性分析中越来越受到重视。

1. 1钢筋本构模型

钢筋是混凝土桥墩结构主要的受力材料，正确模拟钢筋的滞回性能对准确模拟钢筋混凝土结构地震响应十分重要。本文钢筋纤维本构模型采用Giuffre-Menegotto-Pinto［7］模型，见图1（a）。

1. 2混凝土本构模型

在钢筋混凝土结构中混凝土通常包含受约束核心混凝土和无约束混凝土，需要建立2种不同的本构关系。无约束混凝土采用Hognesrad［8］混凝土模型，见图1（b）。约束混凝土采用Mander［9］模型，见图1（c）。

1. 3工程概况

本文采用六跨连续刚构梁桥作为基准桥。桥梁的上部结构为六跨变截面预应力混凝土连续箱梁，跨度为70 m + 4×132 m + 70 m，箱梁为单箱单室截面，箱梁混凝土采用C55混凝土。下部结构共设有7个桥墩，5个主墩为刚构墩，采用双薄壁矩形墩形式，4#～8#桥墩墩身采用矩形箱形截面、C40混凝土。主桥总体布置见图2。

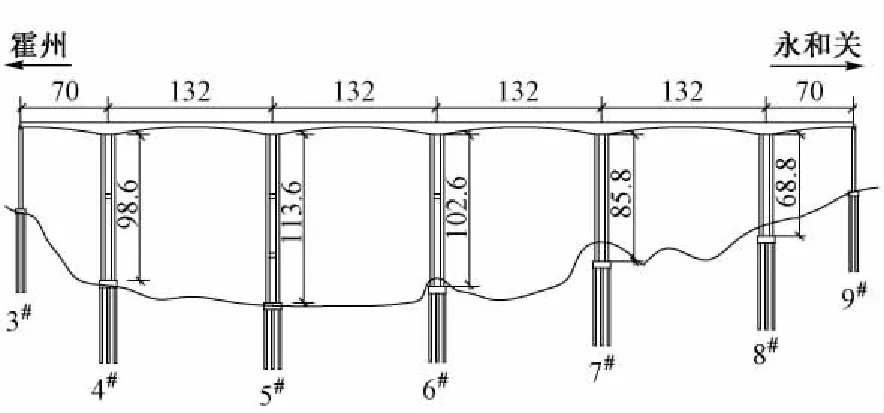
图2　主桥总体布置（单位：m）

1. 4地震动输入

本文研究所依托桥梁位于8度地震区，桥址处为Ⅱ类场地。根据场地条件选取Taft Lincoln School 69 deg地震波作为特征地震动，其加速度峰值为0. 2g（相当于设防烈度为8度的罕遇地震），持续时间为35 s，调整后波形见图3。

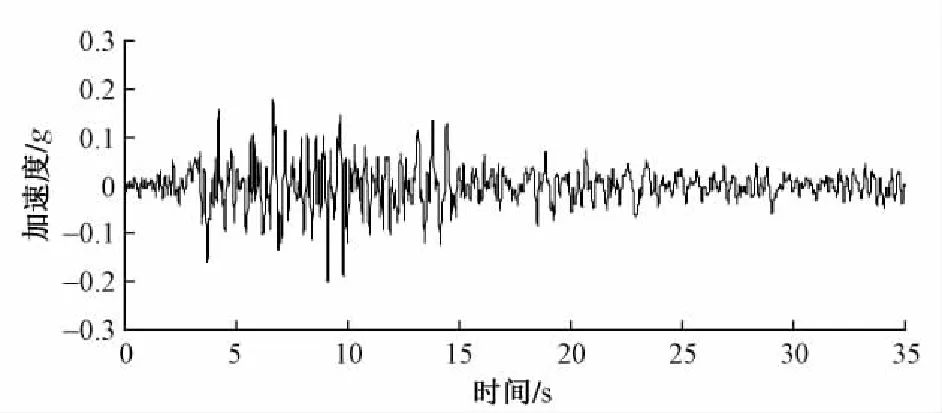
图3　Taft Lincoln School 69 deg地震波调整后波形

2　动力特性分析

采用Midas/civil软件建立有限元模型，主梁采用梁单元模拟，桥墩采用纤维模型单元模拟。结构阻尼比取5％。考虑到场地为Ⅱ类场地，墩底假设为固结，不考虑土-结构的相互作用。前5阶自振周期及其振型见表1。由表1可知模型前5阶振型以主梁横向弯曲为主，表明该桥横桥向抗推刚度较小，在地震作用下主梁易出现侧向偏移、桥墩墩身横桥向弯曲过大等不利情况。第3阶振型为体系纵漂，由于5#墩属于高墩，有可能在顺桥向产生较大塑性转角。

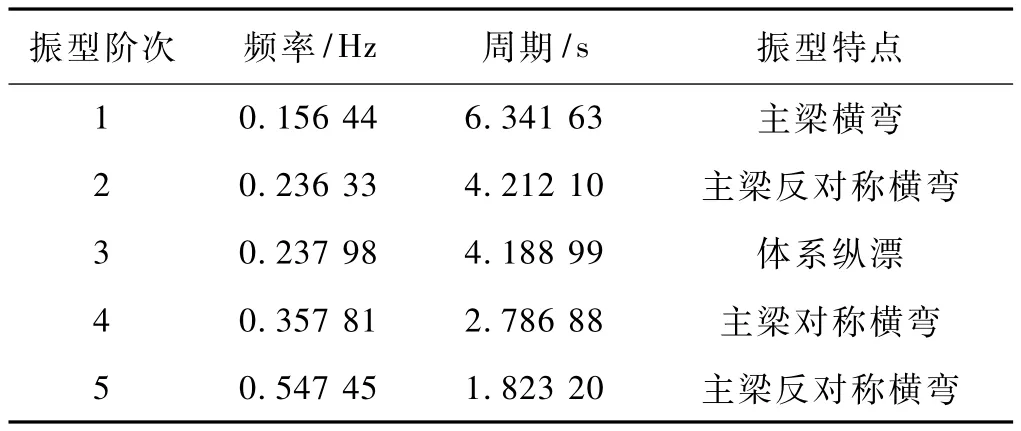
表1　前5阶自振周期及其振型

3　地震响应分析

为对比分析罕遇地震作用下高墩大跨连续刚构桥线性与非线性时程地震响应，分别自顺桥向和横桥向输入加速度峰值0. 2g的Taft Lincoln School 69 deg地震波，计算控制截面位移、内力响应极大值。得出的位移、剪力、弯矩响应的极大值计算结果对比分别见表2、表3、表4。

表2　线性与非线性位移响应极大值计算结果对比　mm

由表2可知，在罕遇地震作用下，各墩墩顶线性和非线性位移响应极大值基本相同。此外，顺桥向、横桥向位移响应特征分别与第3阶振型体系纵漂、第1阶振型主梁横弯一致。表明在罕遇地震作用下无论是否考虑结构非线性行为，结构位移响应仅与结构本身自振特性相关。

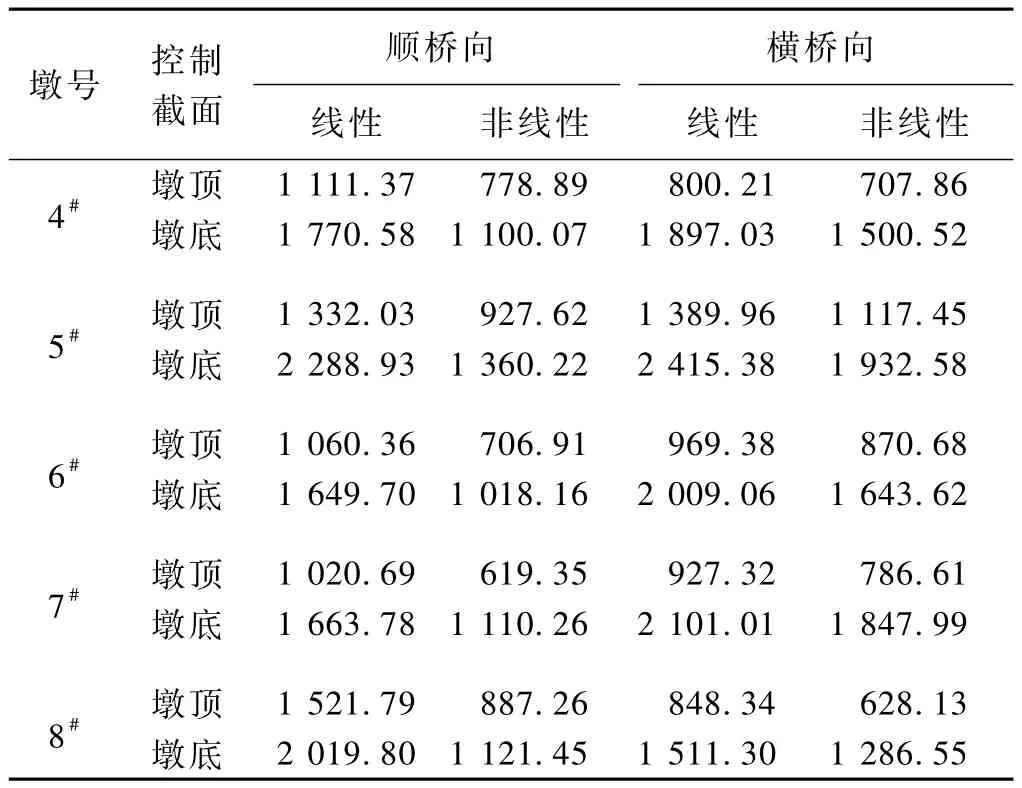
表3　线性与非线性剪力响应的极大值计算结果对比　kN

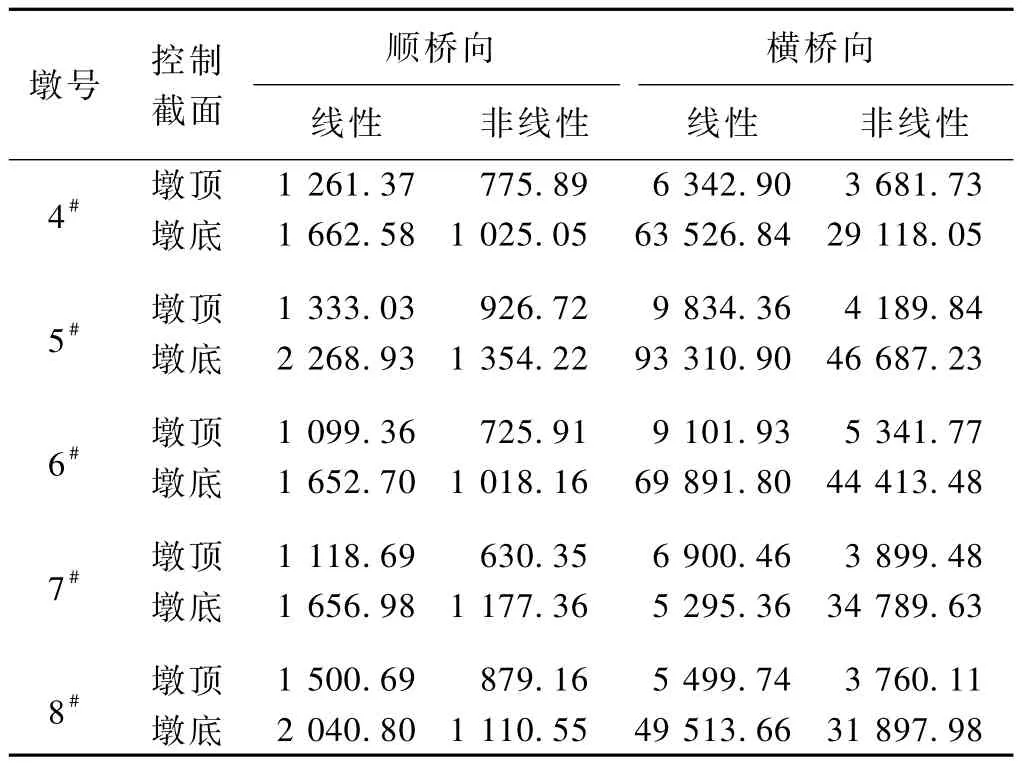
表4　线性与非线性弯矩响应极大值计算结果对比　kN·m

由表3、表4可知，各墩墩顶、墩底剪力和弯矩线性地震响应极大值远大于非线性地震响应。表明桥梁结构在罕遇地震作用下进入非线性阶段，此时线性时程分析计算结果无法真实反映桥梁内力响应情况。这种线性与非线性地震响应位移基本相同而内力差异较大的现象符合基于位移抗震设计的等位移原则［10］。

4墩高对罕遇地震作用下桥梁抗震性能的影响

图4　顺桥向弯矩-曲率滞回曲线

图5　横桥向弯矩-曲率滞回曲线

选取5#墩（最高墩）和8#墩（最矮墩）作为研究对象，分别输入顺桥向和横桥向加速度峰值0. 2g的Taft Lincoln School 69 deg地震波，由非线性时程分析法计算得到5#和8#墩顺桥向墩顶和墩底弯矩-曲率滞回曲线，见图4。5#和8#墩横桥向墩顶和墩底弯矩-曲率滞回曲线见图5。

由图4可知：在顺桥向地震作用下5#墩墩顶的滞回曲线比8#墩墩顶的滞回曲线更加丰满，而8#墩墩底的滞回曲线比5#墩墩底的滞回曲线更加丰满，说明高墩墩顶较矮墩墩顶具有更好的耗能能力，矮墩墩底较高墩墩底具有更好的耗能能力；不同墩高桥墩在顺桥向墩顶、墩底弯矩达到最大时，高墩最大转角远小于矮墩，说明在顺桥向罕遇地震作用下，高墩大跨度连续刚构桥矮墩易进入塑性阶段，而高墩由于柔度大，需要更强地震激励才会进入塑性状态。

由图5可知：在横桥向地震作用下，5#墩无论墩顶还是墩底的滞回曲线均比8#墩相应的滞回曲线更加丰满，说明在横桥向地震作用下，高墩耗能能力更强；不同墩高桥墩在横桥向墩顶、墩底弯矩达到最大时，矮墩最大转角远小于高墩，说明在横桥向罕遇地震作用下，高墩大跨度连续刚构桥横桥向刚度较小，而矮墩横桥向位移响应较小，不易进入塑性阶段。

5　结论

1）模型前5阶振型以主梁横向弯曲为主，表明横桥向抗推刚度较小，在地震作用下主梁易出现侧向偏移、桥墩墩身横桥向弯曲过大等不利情况。第3阶振型为体系纵漂，由于5#墩属于高墩，有可能在顺桥向产生较大塑性转角。

2）在罕遇地震作用下，各墩墩顶线性和非线性位移响应极大值虽基本相同，但内力响应差异较大，表明桥梁结构进入非线性阶段，线性时程分析计算结果无法真实反应桥梁响应情况。

3）在顺桥向罕遇地震作用下，高墩大跨度连续刚构桥矮墩易进入塑性阶段；在横桥向罕遇地震作用下，矮墩横桥向位移响应较小，不易进入塑性阶段。

参考文献

［1］中华人民共和国交通运输部. JTG/T B02-01—2008公路桥梁抗震设计细则［S］.北京：人民交通出版社，2008.

［2］范立础.桥梁抗震［M］.上海：同济大学出版社，1997.

［3］李茜，王克海，韦韩.高墩梁桥地震响应分析［J］.地震工程与工程振动，2006，26（3）：74-76.

［4］李忠献，史志利.行波激励下大跨度连续刚构桥的地震反应分析［J］.地震工程与工程振动，2003，23（2）：68-76.

［5］黄小国，胡大琳，张后举.行波效应对大跨度连续刚构桥地震反应的影响［J］.长安大学学报（自然科学版），2008，28 （1）：72-75.

［6］TAUCER F F，SPACONE E，FILIPPOU F C. A Fiber Beamcolumn Element for Seismic Response Analysis of Reinforced Concrete Structure［R］. Berkeley：Earthquake Engineering Research Center，University of California，1991.

［7］MENEGOTTO M，PINTO P E. Method of Analysis for Cyclically Loaded Reinforced Conerete Plane Frames Including Changes in Geometry and Non-Elastie Behavior of Elements under Combined Normal Force and Bending［C］/ /Proceedings，IABSE Symposium on Resistanee and Ultimate Deformability of Structures，Lisbon，1973：15-22.

［8］HOGAESTED E. A Study of Combined Bending and Axial Load in Reinforced Concrete Members［R］. University of Illinois Engineering Experiment Station，Urbana，IlL，1951.

［9］MANDER J B. PRIESTLEY M J N. PARK R. Theoretical Stress-strain Model for Confined Concrete［J］. Journal of Structrual Engineering，1988，14（8）：1804-1826.

［10］郭磊.桥梁结构基于位移的抗震设计方法研究［D］.上海：同济大学，2006.

（责任审编李付军）

Earthquake Response Analysis of Long-span Continuous Rigid Frame Bridge with High Piers Subjected to Rare Earthquake Shock

TAN Guansheng
（China Railway Siyuan Survey and Design Group Co.，Ltd.，Wuhan Hubei 430063，China）

AbstractA nonlinear model based on fiber model of finite element method（FEM）was built to study the dynamic response of a long-span continuous rigid frame bridge with high piers under rare earthquake. T he dynamic characteristics of the bridge was analyzed. T he dynamic seismic response activated by the longitudinal and lateral earthquake was analyzed based on the linear and non-linear time history analysis. It shows that there is no difference between the linear and non-linear displacement at pier top while the difference is significant for the inner force in the two cases. It suggests that the structure is at non-linear phase under rare earthquake，and thus the linear calculation is not appropriate. Based on the nonlinear time history analysis，the effect of pier length was assessed. Under the longitudinal rare earthquake，the short pier shows significant ductility，and the maximum rotation at long pier is significantly smaller than that at short pier when the bending moment at the pier bottom reaches it maximum. However，under the lateral rare earthquake，the performance of short and long piers goes to the opposite，unlike the dynamic response under the longitudinal earthquake.

Key wordsContinuous rigid frame bridge；Rare earthquakes；Fiber model；Finite element method；T ime history analysis

中图分类号U442. 5+5

文献标识码A

DOI:10. 3969 /j. issn. 1003-1995. 2016. 06. 07

文章编号：1003-1995（2016）06-0027-04

收稿日期：2016-03-19；修回日期：2016-04-06

作者简介：谭冠生（1959—），男，高级工程师。