基于博弈论的全球供应链管理风险分析
戴沛如
摘 要 全球供应链的全球化增加了整条供应管理中的风险。很多企业寻求风险预警机制,在风险出现后寻找降低风险的方法,但这为企业带来损失无法补救。本文基于博弈论思想分析全球供应链管理内生风险,并探讨降低或避免风险发生的对策。
关键词 博弈论 全球供应链 管理风险
中图分类号:C931 文献标识码:A
在全球供应链中各企业都是单独的经济个体,都为了自身的利益而在过程中冒险,即使是合作伙伴关系的企业间也存在着不合作风险。
在此分析在供应链中上下游两个参与者博弈战略过程的两个局中人A、B,总的战略式G={s1,s2;u1,u2},S1={s1}表示A可选择的战略集合,而最优战略记为s*1,它使得u*1获得Eui最大化,同样对于B,战略集合为 S2={s2},而最优战略记为s*2,它使得u*2获得Eui最大化,一方A最优战略意味着:u1(s1*,s2)≥u1(s1',s2) s1'≠s1*;
1纳什均衡分析约束机制及负激励的不完备
为了保证协议有效,必须有一种局中人不可能因单方面违背协议而获益的机制,即形成一种纳什均衡——在非合作博弈论和经济分析里所应用的博弈论思想中的核心地位。因而A给B增加负激励等约束机制,探讨事前控制不完善时(并不是事情发现隐藏信息或行为,而是事后),在负激励约束下双方的博弈行为。
假设在监督情况下B行为被发现的概率q1大[q1>(1- q1)]于不在监督下的被发现的概率q2[q2<(1- q2)]:即q1>q2;同时,q1是随着自身的监督成本增加而概率增大;为减少行为发生,制定约束协议,增加负激励因素U1(U1>0),当B隐藏信息或行为被发现后,将补偿A基本收益。
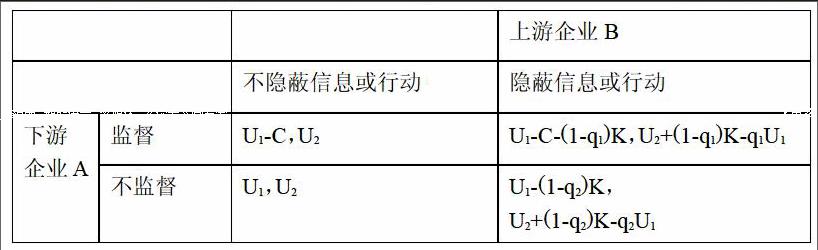
因而在监督情况下,B隐蔽信息后被发现的获益是U2-U1,未被发现时获益U2+K(K为隐信息所得更多的利益,K为正),即获益是:
在A监督情况下:q1(U2-U1)+(1-q1)(U2+ K)= U2+(1-q1)K-q1U1;
而A不监督时:q2(U2-U1)+(1-q2)(U2+ K)= U2+(1-q2)K-q2U1;
而对于A,在B被发现时,其可得到T补偿,在增加负激励的情况下,不管B做出何利方式,A都不会有损失;而对于B,增加负激励等赔偿后,比较B隐藏信息或行动与不隐藏时的利益比较:
监督下B的收益比较:
U2+(1-q1)K-q1U1-U2=(1-q1)K-q1U1 ①
非监督下B的收益比较:
U2+(1-q2)K-q2U1-U2=(1-q2)K-q2U2 ②
在不监督情况下,需要满足(1-q2)K-q2U1大于0,B就会选择隐藏住处或行动,就即:
K> U1*q2/(1-q2);
只要K的值够大,B就会选择隐藏信息或行动;
同样,只有当①大于0时,B就会选择隐藏信息或行动,即当U1/K<(1-q1)/q1;
但前面假设了q1>1- q1,也就是U1/K<(1-q1)/q1<1,U1小于K时,B能通过冒险而不顾整体的利益,而获得自身更大的利益,虽然这是短期行为,但在初期,供应链上更多局中人需要更好的收益。在短期交易中,即使签订了合约(约束机制),双方为了各自的利益,会选择隐藏信息或行动来获得更大收益。例如08年发生的三聚氰胺事件,牛奶供应商看到的是短期利益,不顾长远的合作。
2混合战略纳什均衡分析信息共享
从上面分析,可见事前不可能签订一份如此完备的合同。即使在约束机制下,还可能由于如供应链上不同环节如供应商和制造商的不同目标而利用客观存在的或故意创造信息不对称,从而从对方获取更多的利益,结果造成供应链上的合作伙伴不能达到最优组合。在此运用博弈论思想,寻找约束机制不足情况下降低风险的对策。若一方主动去获得另一方的隐蔽信息需要成本,考虑成本,一方选择监督存在一定的概率。因而,另一方的隐蔽信息或行为的做法被发现也存在一定的概率。
同样,假设在监督情况下被发现的概率q1大(q1>0.5)于不在监督下的被发现的概率q2(q2<0.5):即q1>q2;同时,q1是随着自身的监督成本增加而概增大;
因而在监督情况下,B隐蔽信息后被发现的获益是U2,未被发现时获益U2+ K(K为隐蔽信息所得更多的利益,K为正),即获益是:q1U2+(1-q1)(U2+ K)= U2+(1-q1)K;
而不监督时,B获益:q2U2+(1-q2)(U2+ K)= U2+(1-q2)K;
而在B隐藏信息或行为,不管A是不是监督,只有发现B隐藏信息而进行纠正行为后才获得U1,而没发现,A都要损失K(B所多得的利益),而监督更增加成本,总的来说A的实施监督和不监督时的获益分别是:
q1(U1-C)+(1-q1)(U1-C-K)=U1-C-(1-q1)K;
q2U1+(1-q2)(U1-K)=U1-(1-q2)K;
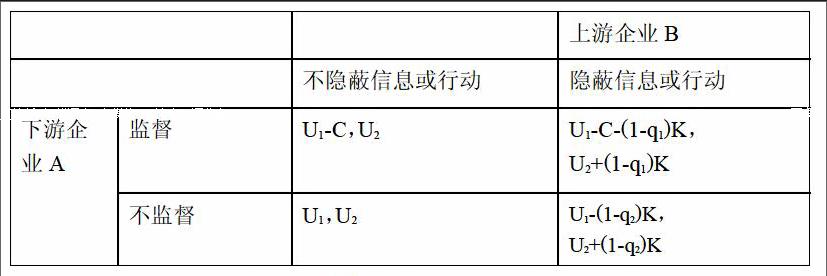
对于供应链上两方,在没有外部约束时,两方博弈矩阵如图1所示:
对于B,在A不采取约束机制而B又不需(下转第132页)(上接第113页)要承担风险的情况,不管理A是否采取监督,B会选择隐藏信息或行为从而获得比不隐藏信息或行为时更多的利益,也就是说没有约束机制,B总会选择隐藏信息或行为;而对于A,既然B总选择隐藏,因而B隐藏了信息或行为,A要分析如何能做出最优策略,比较A监督和非监督两种情况得益:
U1-C-(1-q1)K- [U1-(1-q2)K]=(q1- q2)K-C
当(q1- q2)K-C>0时,A采取监督;当(q1- q2)K-C<0时,A不采取监督;对于A由于发现的概率不确定,不存一个纳什均衡。
而发现信息隐藏的概率随着自身C的增加而加大,通过自身成本增加而提高监督情况下发现概率,这对企业来说都是很大的障碍。一旦B隐藏信息或行为做法给A所造成的负效果很大时,A一定会采取监督以避免严重后果。比较好的情况是,监督成本或获得信息成本尽量降低而又可以提高监督下信息获得量,从而提高发现隐藏信息的概率。最好的情况是,在不实行监督而发现概率跟实行监督时概率一样,此时,B即使获得额外收益的值也相对较少,为了长期合作,B不会为了更少的收益而损害双方的合作关系。因而在供应链管理中,更多需要双方的信息共享和第三方信息协同平台,在这种平台方式下,不管需要与多少家供应链伙伴进行信息交换 ,在技术上,企业只需要采用一种数据标准就可以与第三方信息协同服务平台进行系统对接,而不需要再与供应链伙伴一一进行协商。在供应链管理中,必须增加供应链节点企业问的联系与合作,提高信息共享程度,用覆盖整个供应链的决策系统代替缺乏柔性和集成度差的决策体系。一体化、系统化管理是非常重要的,这些应用系统将供应链网络上所有的参与者连接起来,降低全球供应链管理风险,把复杂的全球供应链管理得当。
3动态博弈分析信誉机制
当合约不完备,而监督成本过高时,需要降低供应链管理风险更需要局中人的长期合作。供应链管理是建立在一个合作信念上的,合作行为将减少风险,即效率能够通过分享信息和共同计划使整体供应效率得到提高。如果双方有机会长期博弈,合作仍然可以通过信誉机制实现。
假若第一次合作B不守信用,将被A终止其合作关系,B只得短期的收益15;若B诚信,使得双方受益,他将会获得 的长期合作机会,因而B长期收益将会是:
10+10 +10 2+10 3+10 4+……=10/(1- )
只要10/(1- )≥15,即 ≥0.333,B企业就可以多次合作中获益。因而,从长远的利益来看,供应链上的局中人应建立信誉机制。一旦偷懒或不合作被发现,其余所有企业会一致决定将该企业开除出供应链,而在全球供应链中,跟跨国企业合作,这将会是国内企业的优势,建立信誉机制,不仅是一次合作方知道其信度,同一供应链上的其他局中人也会知道其信誉,这影响着一方的长远发展,不守信将会是企业长期生存的威胁。偶尔的违约所得却是冒着失去与其伙伴进行长期有利可图的合作关系和良好的声誉的危险,这会压制着机会主义行为的发生。
4总结
由于全球供应链的跨国度等因素,使其比国内供应链面临着更大的风险。基于博弈论,在全球供应链管理中风险,可考虑建立完善的合同,使得在合作后追究一方的责任,降低道德风险;在整条全球供应链管理中,更需要供应链各节点企业的建立信誉机制,跨国间能获得企业的信誉情况,在供应链节点企业间建立战略合作的伙伴关系。
参考文献
[1] 吴德庆,马月才,王保林.管理经济学(第五版)[M].中国人民大学出版社,2010.
[2] 刘永胜.供应链风险预警机制[M].中国物资出版社,2007.
[3] 马永生.供应链管理中信息共享风险及弱化[J].煤炭经济研究,2006(8).

