基于博弈论的建筑工程投标报价最优化分析

潘庆红

（嘉善县公共资源交易中心 浙江省嘉兴市 314100）

基于博弈论的建筑工程投标报价最优化分析

潘庆红

（嘉善县公共资源交易中心 浙江省嘉兴市 314100）

随着社会的发展，大力推动了我国建筑行业的发展。在建筑工程项目中，前期的招标过程在整个过程中占有一定的地位，而在建筑项目进行竞标的过程中，投标报价起到关键的作用。因此，本文就对基于博弈论的建筑工程投标报价最优化进行分析为企业在竞标的过程中提供有效的依据。

博弈论；建筑工程；投标报价；最优化

引言：博弈论又称为赛局理论，其主要对行为发生作用时的决策以及这种决策的均衡问题进行的研究，在将其应用到建筑工程投标报价中，就是研究在竞标市场中企业如何获得到最大的利益。而在当前阶段中，建筑工程逐渐的向着复杂的方向发展，在这种情况下，加强对博弈论的建筑工程投标报价最优化分析成为了必然趋势。

一、招标过程中的博弈利益最优化关系

在建筑工程招标的过程中应用到博弈论的方法时，就将会产生相应的博弈关系，其主要分为了招标方与投标方的博弈以及投标方与投标方的博弈。对于投标方而言，就是以最低的价格将施工项目承包下来，获得最大化的经济效益；而对招标方而言，是以最高的价格将施工项目承包给投标方，以使自身的经济利益最大化[1]。在进行招标的过程中，各招标方往往要面对多个投标方，就可以建立相应的博弈收益矩阵，其中A代表了投标方，B代表了招标方，W代表投标方的经济效益，U代表了招标方的经济效益。在投标方想要赢得这场竞标战争，同时要想将利益进行最大化，就要打败其他的投标方，而且，还必须达到招标方的要求。

二、招标方与投标方的博弈分析

（一）假设条件

在一项建筑施工项目招标过程中，假设招标方有 1个单位参加，投标方有n（n≥3）个单位参加，在进行投标的过程中，经过招标方计算，将第i个投标报价定位为预期价值vi，这一数值只有招标方了解，而且vi还要遵守指数分布原则。在一般情况下，投标方是由小到大进行报价的；并且要将投标方i的预算价值进行一定的函数调整，用bi（vi）表示；并假设投标方的报价范围为b，招标方的预算价值为v；而且在进行招标的过程中，严格的按照相关的规定完成的，不存在串标的现象；同时规定不会出现一样的报价；投标方在选择出合理的投标方后，就可以根据以下函数公式进行收益计算：

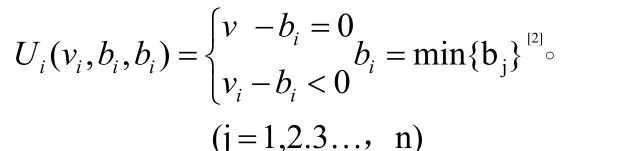
（二）博弈论模型的建立

在进行建筑工程招标之前，招标方不了解自己的竞争对手有哪些，只能将其一段时间内的报价资料进行分析，得到一个大概的报价范围，因此，使用博弈论的方式来进行建筑工程项目的招标时，属于不完全静态博弈[3]。

在建立模型时，首先就要对不完全静态博弈理论进行分析，建立出有效的博弈策略范围，构建出符合要求的报价函数关系 bi（vi），同时构建出投标方的报价策略 bj（vj），然后结合合理最低原则，得到相应的收益期望函数：并且，要保证招标方以最低的价格将项目承包出去时，还要获得最大的经济效益，则由遵守的服从指数得到：然后对U取最大值，可以得到：然后取b最优值，令 vb=Φ )( ，可得，最后对投标报价进行计算，可令C0=0，得到最终的博弈论模型：

（三）模型分析

由上述模型函数公式我们可以发现，bi与vi与参与的投标方数量有关，即投标方越多，其数值越小，同时参与的投标方越多，b与v越接近。在实际的招标过程中，投标方报出的价格通常都要高于其计算出的预算价格，如果参与的投标方不多时，更加明显的体现出来其中的差距，只有参与的投标方较多时，差距才不会很明显。因此，在招标的过程中，参与的投标方越多，招标方可以获得更大的利益。

三、投标方与投标方的博弈分析

（一）假设条件

在一项建筑施工项目招标过程中，假设招标方有 1个单位参加，投标方有 n（n≥3）个单位参加，在第i个投标方进行速算时，计算出其工程成本为ci，并且这一数值只有投标方自己了解。在一般情况下，而且ci还要遵守Exp(λ)指数分布原则，投标方是由小到大进行报价的；并且要将投标方i的预算价值进行一定的函数调整，假设投标方的报价范围为b，成本范围为c；而且在进行招标的过程中，严格的按照相关的规定完成的，不存在串标的现象；同时规定不会出现一样的报价,并将投标所用的成本排除；投标方在选择出合理的投标方后，就可以根据以下函数公式进行收益计算：

（二）博弈论模型的建立

在进行建筑工程竞标的过程中，各个投标方单独的进行投标工作，并且不了解其他投标单位的报价，根据自己的实际情况来进行报价，在招标工作完成后，各投标方仍然不了解其他竞争者所采用的报价。因此，其也属于不完全静态博弈。

在建立模型的过程中，首先要建立出有效的博弈策略范围，构建出符合要求的报价函数关系 bi（ci），同时构建出投标方的报价策略 bj（cj），然后结合合理最低原则，得到相应的收益期望函数：由遵守的服从指数得到：为投标方i报价的逆函数，为了使投标方在招标过程中花费最低成本获得胜利，同时得到的利益最大，可以令（b）=b-1（b）得到：然后对U取最大值，可以得到：然后取 b最优值，令（b）=c可得：最后对投标报价进行计算，可令C0=0，得到最终的博弈论模型：

（三）模型分析

有上述的模型函数公式可以发现，投标方越多报价就越低，当参与的投标方接近无限大时，投标方的报价与成本基本相同。因此，可以得出结论，参与竞标的竞标方越多，招标方的利益能够获得最大值。

总结：随着建筑行业的不断发展，博弈论在投标报价进行了应用，使招标的过程更好地进行。但随着人们自身综合素质的不断提高，招标的经验不断地增加，使得招标过程中会逐渐出现新的问题，因此，我们不能满足与此，应该以当前的博弈论为基础，对其进行改善与加强，形成一种新的投标报价方法，在社会发展的各阶段中，使建筑行业招投标活动都能够很好的进行。

[1]彭荔，王美华.基于经评审的最低投标价法的工程项目投标报价策略研究[J].经营管理者，2016，01（03）:1.

[2]黄敏，吴立，樊友川.基于博弈论在交通工程投标报价分析中的研究[J].公路工程，2016，04（01）:183.

[3]金灵.建筑工程投标报价的策略和报价编制的技巧分析[J].经营管理者，2012，07（04）:234.

[4]陈起俊，梁宝栋.BQ计价模式下工程项目投标报价博弈模型研究[J].科技进步与对策，2012，11（18）:62.

TU43

B

1007-6344（2016）08-0181-01