树枝直刃剪切数学模型与试验

王慰祖，吴良军，杨　洲，陆华忠，汪刘一，郭晓伶

(1华南农业大学 工程学院, 广东 广州510642; 2 广东交通职业技术学院 汽车与工程机械学院， 广东 广州 510650； 3 广东省农业科学院， 广东 广州 510640)



树枝直刃剪切数学模型与试验

王慰祖1，吴良军2，杨洲1，陆华忠3，汪刘一1，郭晓伶1

(1华南农业大学 工程学院, 广东 广州510642; 2 广东交通职业技术学院 汽车与工程机械学院， 广东 广州 510650； 3 广东省农业科学院， 广东 广州 510640)

摘要：【目的】基于材料力学和弹性地基梁理论对直刃刀片剪切树枝过程进行理论建模，并根据该模型计算出直刃刀片剪切树枝所受的剪切力。【方法】以石硖品种龙眼树枝为试验材料，利用万能材料试验机和摩擦试验台等仪器测定龙眼树枝的相关力学特性参数和滑动摩擦因数，测量并用模型计算树枝不同含水率(w)、直径和不同刀片刃角下动刀片剪切龙眼树枝的峰值剪切力，剪切试验所用刀具的刃角分别为10°、20°和30°。【结果】当树枝直径为20.4 mm、相对含水率为76%、刀片刃角为20°时，刀片剪切力理论计算曲线与试验曲线趋势一致，峰值剪切力的误差约为2.3%；当树枝直径为15.3 mm，刀片刃角为20°，且树枝含水率大于纤维饱和点(30%)时，刀片峰值剪切力随含水率升高而增大，计算值在试验值的误差范围内；当树枝直径为24.6 mm、含水率为76%，且刀片刃角从10°增大到30°时，峰值剪切力显著增大，计算值处于试验值的误差范围内。【结论】该理论模型可用于预测剪切力并分析不同力学参数对峰值剪切力的影响，为修剪机具剪切机构的设计和优化提供参考。

关键词：数学模型；直刃刀片；剪切；含水率；刃角，龙眼树枝；弹性地基梁理论

在果园管理中，需按季节对果树进行修剪[1]。目前南方果园修剪主要依靠传统的人工手动作业，劳动强度大、效率低、成本高。为降低修剪作业的劳动强度和提高作业效率，气动和电动修剪作业在国内逐步得到推广和应用[2]。龙眼树枝硬度高，剪切强度大，现有气动和电动修剪机具的剪枝能力尚不能完全满足使用要求，探索降低刀片剪切力的途径和优化剪切机构设计以提高机具的作业性能具有现实意义[3- 6]。

修剪过程是树枝与机具工作部件(动、定刀片)持续相互作用的复杂过程。刀片剪切力是设计刀片结构和参数的依据，其大小直接关系到刀片的使用寿命及修剪机具的作业效率和质量，推导树枝剪切力理论计算公式可为经验公式的建立提供理论依据，为提升修剪机具的作业性能和效率提供理论指导。刘庆庭等[7- 8]对甘蔗的切割机理进行了系统的理论和试验研究；吴子岳等[9]研究了玉米秸秆的切断速度和切断功耗；Igathinathane等[10]研究了棉秆的剪切过程，认为剪切行为包含压缩和剪切2种效应；玉米秸秆的切割力和切割功耗已有理论和试验研究[11-13]；Yumnam[14]对直刃刀切割棉花茎秆进行了力学建模，但未进行试验验证；赵湛等[15]对超级稻单茎秆进行了切割性能试验；Minna等[16]研究表明刀片涂层对降低刀片剪切力有重要作用；Chattopadhyay等[17]建立了一种高粱茎秆甩刀式切割的数学模型。上述研究主要集中在刀片切割力功耗研究、切割运动参数和刀片组合方式优化等方面。切割理论研究方面有力学建模的尝试，鲜见直接用于预测刀片剪切力并通过具体算例进行模型预测准确度和计算精度分析方面的报道。本文基于材料力学和弹性地基梁理论提出一种树枝直刃剪切的计算模型，并以石硖品种龙眼树枝作为算例，对模型预测精度进行试验验证，以期为设计和优化修剪机具的剪切机构提供参考。

1力学分析

为简化力学分析过程，作如下假设：树枝为圆柱形的弹性体，其材料性质满足弹性力学基本假设；动刀片为刚性体，剪切树枝过程中发生的变形忽略不计；动刀片在剪切树枝过程中处于平衡状态，即匀速剪切树枝。所计算的剪切形式见图1，动、定刀片均为直刃，定刀片起支撑和辅助剪切的作用，动刀片在外载荷的作用下作铅垂向下运动并最终剪断树枝。

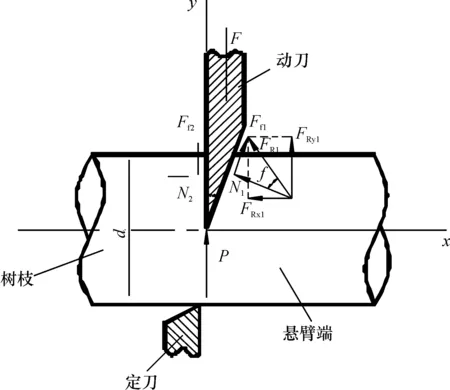
图1　树枝直刃剪切示意图

1.1剪切过程中动刀片的受力分析

如图1所示，树枝被动刀片切开至某一深度时，刀片受到的作用力包括树枝对刀刃的阻抗力P；刀片左侧树枝对刀片的正压力N2和摩擦力Ff2；刀片右侧树枝对刀片的正压力N1和摩擦力Ff1；刀片受到的外负载F。右侧树枝对刀片的正压力N1和摩擦力Ff1可以合成为总反力FR1，可以将该力分解为水平方向力FRx1和垂直方向力FRy1，则存在以下各式：

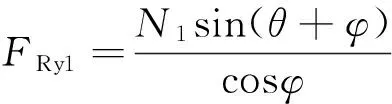
(1)

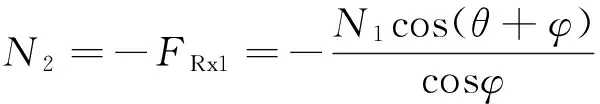
(2)

Ff2=N2μ=N2tanφ，

(3)

F=P+Ff2-FRy1，

(4)

式中，θ为动刀刃角，(°)；μ为树枝与刀片的摩擦因数；φ为树枝与刀片的滑动摩擦角，(°)。

1.2刀片所受树枝正压力的确定

图2为树枝剪切横截面示意图。由图2可知，圆形横截面下方实线围成的面积为未剪切部分。设树枝的半径为r(r=d/2)，mm；刀片切入深度为a，mm；未剪切部分树枝的高度为t，mm；未剪切部分横截面的形心为G；刀刃与树枝的接触线长度为L，mm；树枝被切开部分的面积为A，mm2；由几何关系得如下算式：

t=2r-a，

(5)

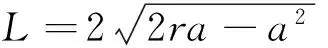
(6)

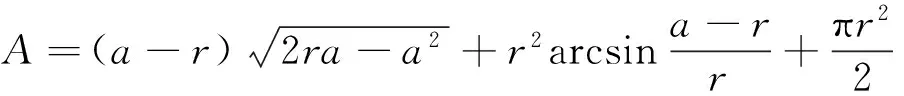
(7)

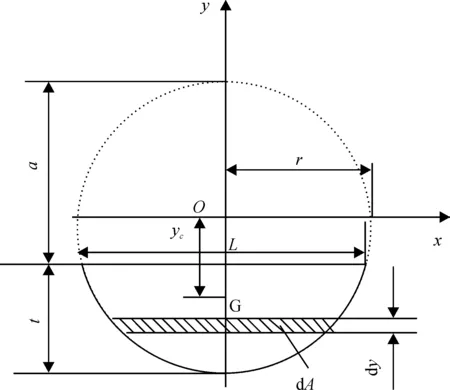
图2　树枝剪切截面示意图

在图2中取与x轴平行的微元，其厚度为dy，面积为dA。当刀片切入树枝后，刀片本身存在的厚度将挤开两侧的树枝，两侧的树枝将受到的力传递给未被切割的树枝，如果将未切割的树枝整体看成梁1，则梁1将在该力的作用下产生弯曲，如图3所示。

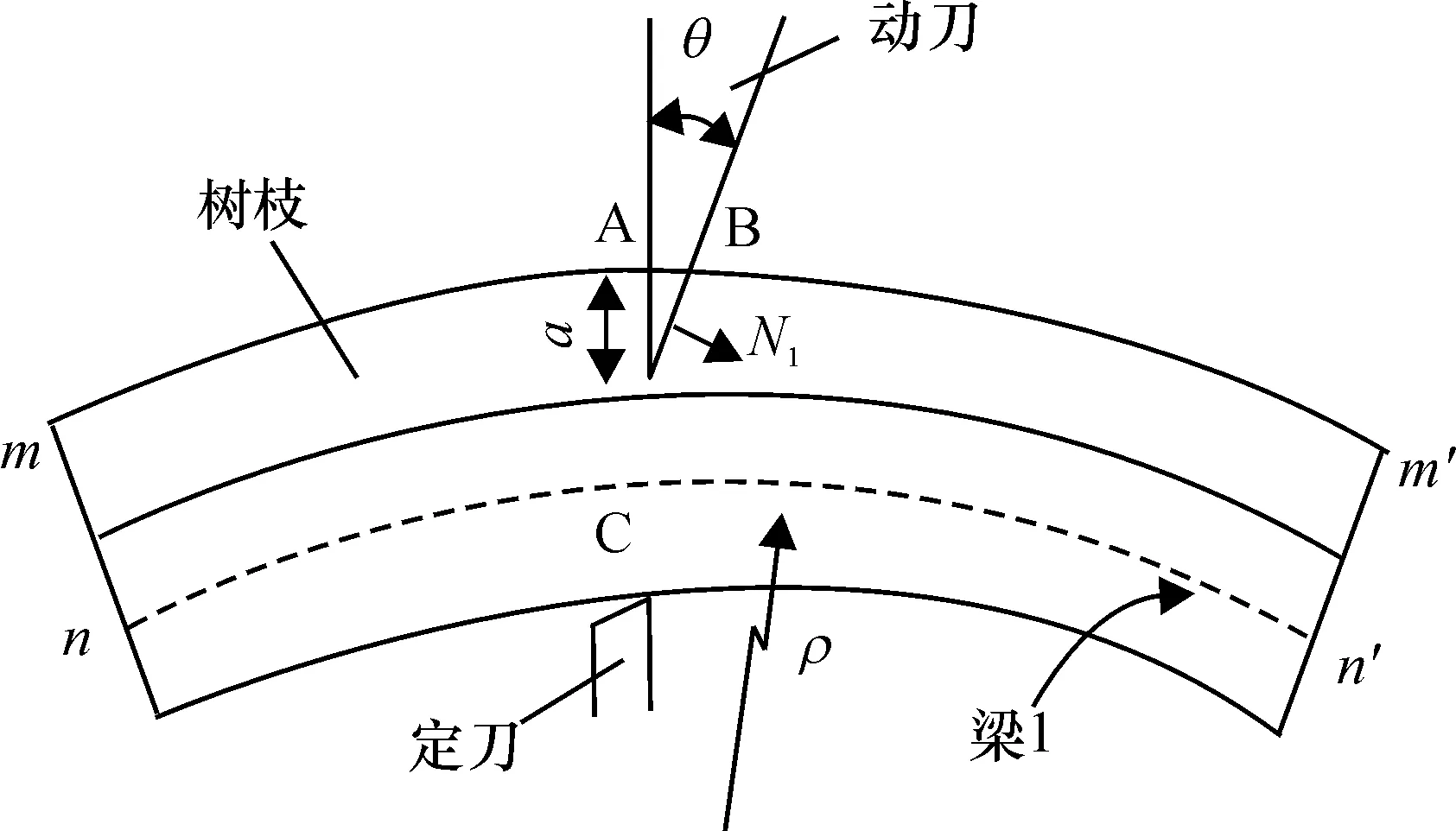
图3　梁1受动刀片挤压而弯曲

Fig.3Bending of beam 1 caused by extrusion of a moving blade

梁1的截面积对x轴的面积矩为Sx可表示为：

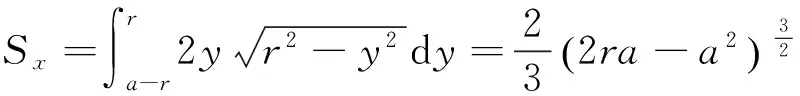
(8)

该面积的形心G点到x轴的距离yc为：

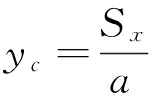
(9)

根据惯性矩的定义，梁1的惯矩Ix可表示为:

Ix=∫A(y-yc)2dA=

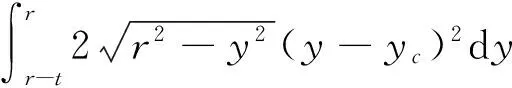
(10)

为简化计算，使用参数B1，B2和B3，单位均为m4，令：

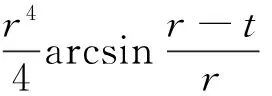
(11)

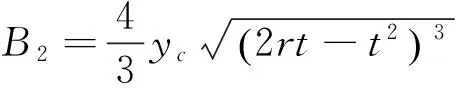
(12)

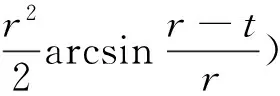
(13)

综合将式(10)积分后简化为：

Ix=B1-B2+B3，

(14)

设梁1的中性层为通过弧nn′的纤维层，并设受到弯曲变形影响的部分在中性层上的弧长nn′为c，弧线nn′对应的角度为γ，则AB 2点间的距离Δ为：

Δ=atanθ，

(15)

受弯曲影响的弧长c与未切割树枝的高度t有关，随着t的减小，c也会变小，如果设c=αt，α为系数，则有：

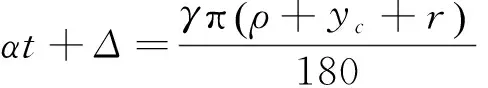
(16)

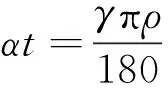
(17)

由式(15)～(17)可得梁1轴线的曲率半径ρ：

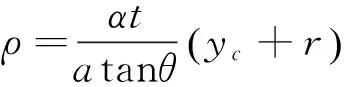
(18)

由材料力学梁的弯曲理论可知：

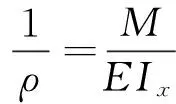
(19)

式中，E为树枝的顺纹抗拉弹性模量，Pa；Ix为梁1截面的惯性矩，mm4；M为作用于梁1的弯矩，N·m。

由式(18)和式(19)可求出作用于梁1的弯矩M。设刀刃的高度为j，则定刀支持点C到正压力N1的距离l可以按下式计算：

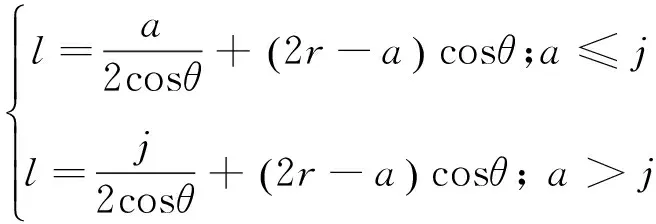
(20)

式中，l为定刀支持点C到正压力N1的距离，mm；a为动刀片切入深度，mm；r为树枝半径，mm；θ为动刀刃角，(°)； j为刀刃的高度，mm。

所以正压力N1可表示为：

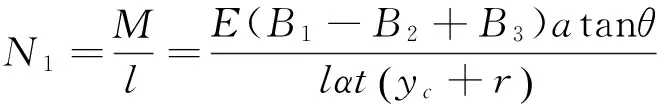
(21)

1.3刀刃所受阻抗力的确定

刀刃厚度一般较小，当刀刃作用于树枝纤维时，可以看成是集中力。研究[18]表明，树枝纤维在刀刃的挤压下，发生变形，当变形足够大时，纤维会被拉断，如图4所示。

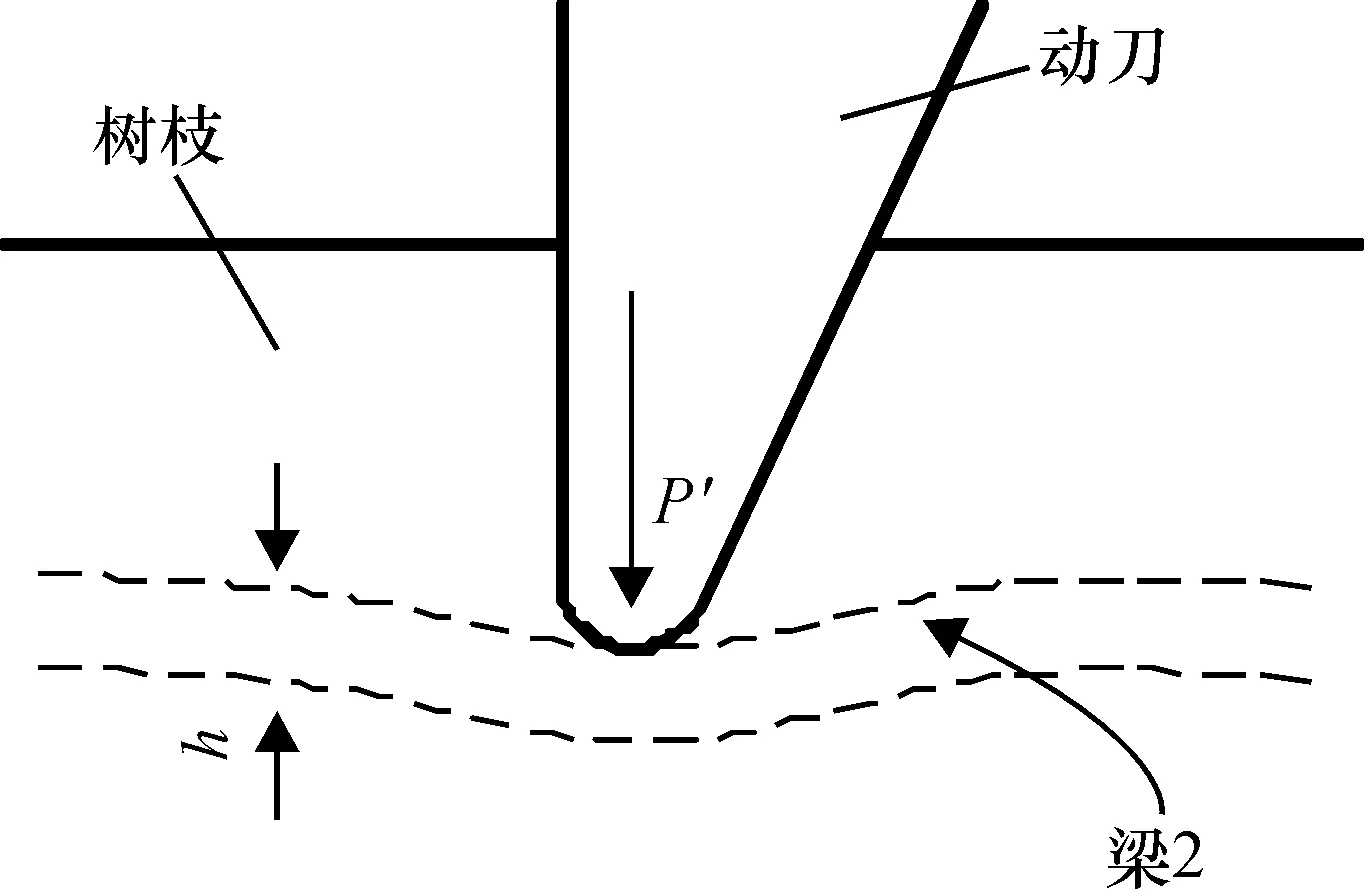
图4　树枝纤维受力变形示意图

Fig.4Diagram showing deformation of the branch fiber under stress

将刀刃直接作用的纤维部分看成梁2，其厚度为h。动刀刀刃对下方纤维的作用力P′是P的反作用力，单位为N，二者大小相等，方向相反。

弹性基础梁理论适用于连续的弹性体为基础的结构计算，常用于路面、板材、地基等[19]，因梁2下方的树枝为连续的弹性体，故可将梁2简化为以梁2下方树枝体为基础的弹性基础梁，由有限长弹性地基梁理论[20]，在力P′的作用下，梁2在刀刃处的应变ε约为：

ε=1.055 P′β/2k，

(22)

式中，k为梁2下方树枝体的地基反力系数，N·m-2；β为特征系数，m-1，其大小为：

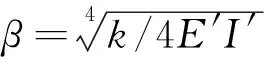
(23)

式中，E′为树枝的横纹抗压弹性模量，Pa；I′为梁2截面的惯矩，m4；由于h很小，所以近似有：

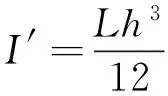
(24)

梁2基础上的应力σ为：

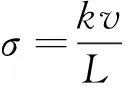
(25)

式中，L为刀刃与树枝的接触线长度，mm。当梁2的纤维由于变形被拉断时，σ即等于木材的顺纹抗拉强度σ0，Pa。

对于树枝，考虑到其各项异性的材料特点，研究认为k可以用下式计算[21]：

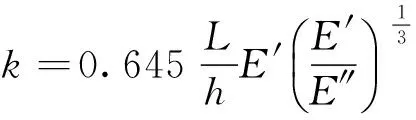
(26)

式中，参考木材切削理论[26]，h=0.076 mm，E″为树枝顺纹抗弯弹性模量，Pa；E′/E″对于含水率饱和的木材一般为0.08～0.10。

根据式(22)～(26)，在梁2纤维被拉断的临界点时，木材对刀刃的阻抗力P可以表示为：

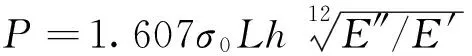
(27)

1.4动刀片剪切力计算公式的建立

根据式(1)～(4)及式(21)、式(27)，可将动刀片所受外载荷F表示为：

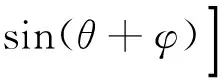
(28)

式中，θ为动刀刃角，(°)；φ为树枝与刀片的滑动摩擦角，(°)；L为刀刃与树枝的接触线长度，mm；h为梁2的厚度，mm；σ0为木材的顺纹抗拉强度，Pa；E为树枝的顺纹抗拉弹性模量，Pa；E′为树枝的横纹抗压弹性模量，Pa，E′为树枝顺纹抗弯弹性模量，Pa； t为未剪切部分树枝的高度，mm； l为定刀支持点C到正压力N1的距离，mm；a为动刀片切入深度，mm；r为树枝半径，mm；yc为形心G点到x轴的距离，mm；B1，B2和B3为参数，单位均为m4，参见式(11)～(13)

2材料与方法

2.1试验材料

试验所用树枝均采自广东省农业科学院果树研究所龙眼果园，采试样种为石硖，树龄30年，行距5 m、株距4 m，采样果树8棵，所采树枝尽可能通直，直径变化连续均匀，无病虫害和少节，剪去小分枝后将树枝编号并用小枝叶覆盖，装入帆布袋密封保存。树枝实测含水率(ω)为62%～88%。

2.2摩擦试验台及试样制作

摩擦试验在自制的试验台[22]上进行，金属摩擦盘采用和刀具同样的材料GCr15钢，经磨削后粗糙度为3.2 μm。树枝试样采自直径为35～50 mm的龙眼树枝，经车削加工成直径为18 mm，高度为60 mm的圆柱形试样，试样端面采用45°车刀加工成平面。摩擦接触方式为圆柱形树枝试样端面与金属盘表面接触，摩擦试验台见图5，金属盘由可调速电机通过同步带传动带动，树枝试样由试样夹夹持并用螺栓固定。

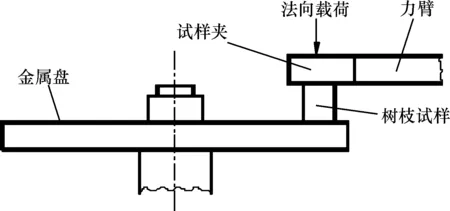
图5　摩擦试验台示意图

金属盘逆时针转动，其对树枝试样施加的摩擦力造成力臂的变形并作用于固定的位移传感器(Linear variable differential transformer, LVDT)，LVDT的探测头在力臂的作用下发生位移，该位移信号被数据采集器实时采集后输入电脑，并通过软件显示。

试验时，先开动电机让摩擦副磨合约10 s，再进行正式试验，采集60 s内的数据，然后更换试样进行下一次试验，单因素试验每一水平重复试验5次。试验分别采用平均含水率(w)为50%、58%、66%和80%树枝试样进行，将试样在空气中放置一段时间即可获得较低含水率的试样。

2.3含水率测定

含水率的测量参照GB/T 1931—2009[23]，摩擦试验后立即将试样放入(103±2) ℃ 的电热恒温鼓风干燥箱中干燥24 h，设烘干前后单个试样的质量分别为m1和m2，单位为g，则试样相对含水率(w)用下式计算，

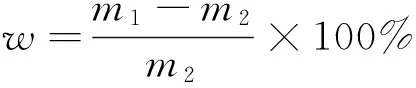
(29)

2.4龙眼树枝力学特性试验

龙眼树枝的力学特性试验使用WD-E型精密微控电子式试验机(广州市广材试验仪器有限公司)，试验机的传感器量程为20 kN，分辨率1/120 000，力值精度0.5%，位移精度0.3%。

按照要求[24-26]测定树枝的力学特性参数和试样制作，所测参数包括顺纹抗拉强度、顺纹抗压弹性模量和横纹抗压弹性模量。

进行剪切试验时，将自制剪切试验台安装在万能材料试验机上，使用刃角分别为10°、20°和30°的动刀片进行剪切试验，刀片如图6所示。设置试验机切割速度为250 mm·min-1，数据采样速度为10 个·s-1，单因素试验每一水平重复试验5次。

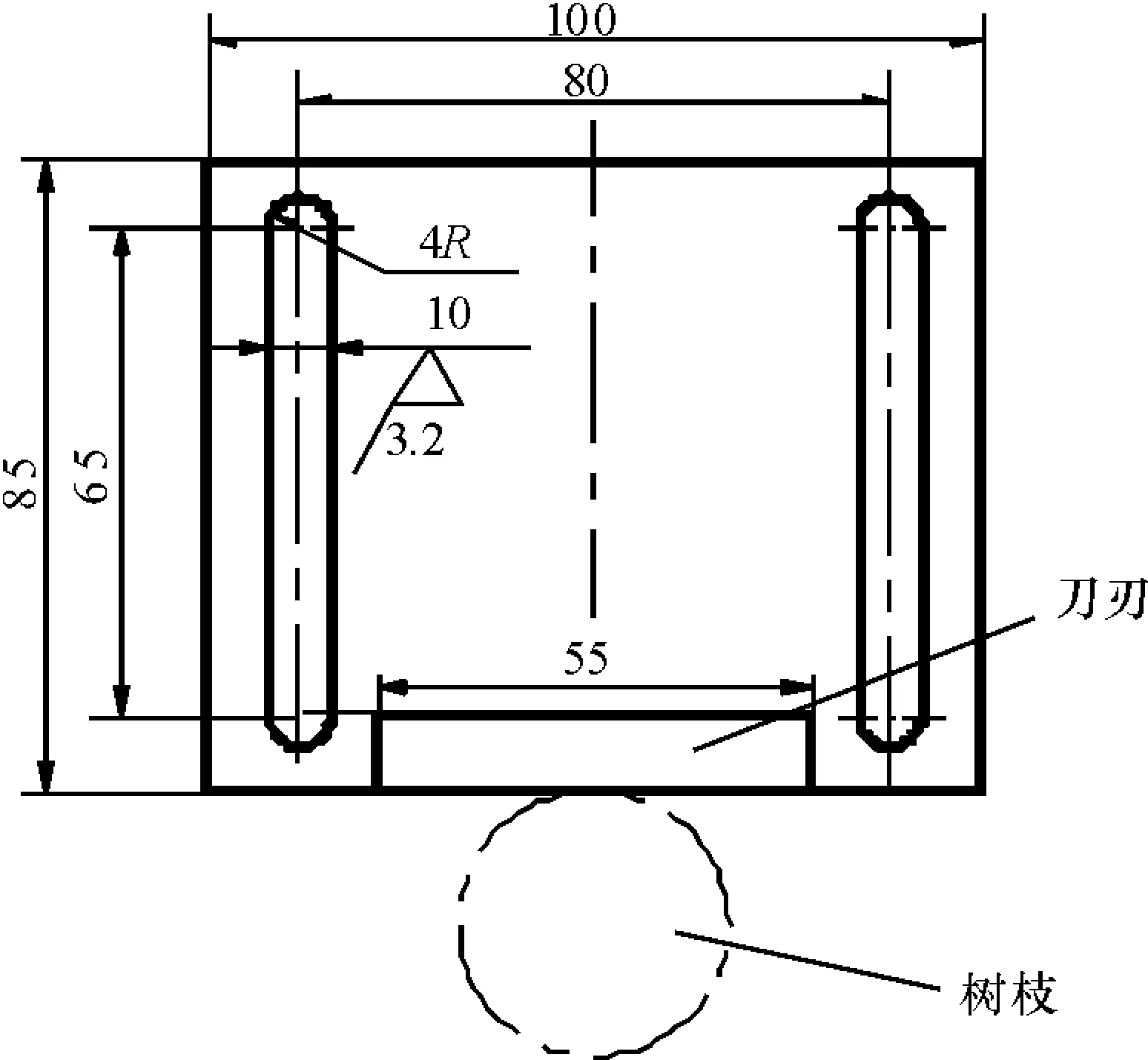
R=5 mm。

3结果与分析

3.1刀片与树枝的摩擦因数

动刀片与树枝摩擦因素试验中摩擦试样的直径为18 mm，高度为60 mm；金属摩擦盘的材料为GCr15钢；金属摩擦盘相对树枝试样的滑动速度为0.04 m·s-1。由图7可知，树枝含水率对摩擦因数有显著影响，摩擦因数随含水率的增加而增大。将树枝含水率与摩擦因数均值进行曲线回归拟合，拟合结果表明指数函数关系具有较好拟合优度，拟合方程和判定系数见图7(P<0.05)。结果表明，树枝含水率与摩擦因数呈显著指数函数正相关关系。

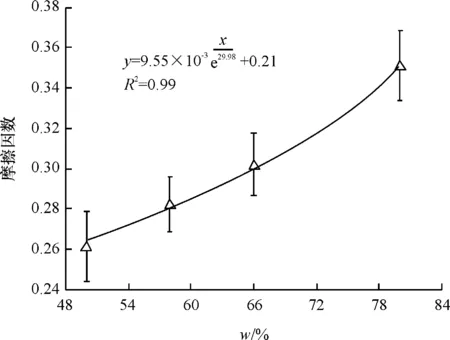
图7　含水率(w)对滑动摩擦因数的影响

3.2龙眼树枝力学特性参数

当木质材料的含水率在纤维饱和点(30%)以下时，其力学参数随含水率的升高而减小，而含水率超过纤维饱和点时，其主要力学特性参数不再发生显著变化[27]。试验结果表明，龙眼活体树枝含水率为62%～88%，大于纤维饱和点，可近似认为树枝力学特性参数基本不变。测得的龙眼树枝横纹抗压弹性模量E′为216.28 MPa，顺纹抗拉弹性模量E为493.07 MPa，顺纹抗拉强度σ0为52.12MPa，含水率为73.34%。

3.3模型计算结果与试验结果对比分析

3.3.1刀片剪切树枝过程的剪切力基础参数带入式(28)可计算出剪切树枝时所需的剪切力。利用本文力学模型，按力学参数进行计算，并取E′/E″=0.09，系数α=0.65，当树枝直径d=20.4 mm，树枝含水率(w)为76%，刀片刃角为 20°，动刀剪切速度为 250 mm·min-1时，计算结果与试验结果的比较见图8。

由图8可知，计算曲线与试验曲线趋势相同，计算曲线的剪刀力最大值较试验曲线的提前出现，说明存在误差，产生误差的原因可能有：建模时假设树枝材料均匀，但实际树枝材料的髓部和木质部、韧皮部材料参数存在差异；建模时忽略了树枝受压后的整体变形，从试验数据可以看出，剪切的开始阶段测得剪切力上升较慢，这个阶段很可能是由于树枝受压发生变形引起的；树枝材质在受力时，各层之间因为受力不均会发生变形，建模时假设各层只发生整体弯曲变形，没有考虑各层因挤压产生的厚度方向的变形及相互影响；一般的工程计算认为，地基反力系数不变，但当弹性基础梁的基础部高度小于临界值时，其地基反力系数会显著增大，在树枝的剪切过程中可能存在类似情况[28]。

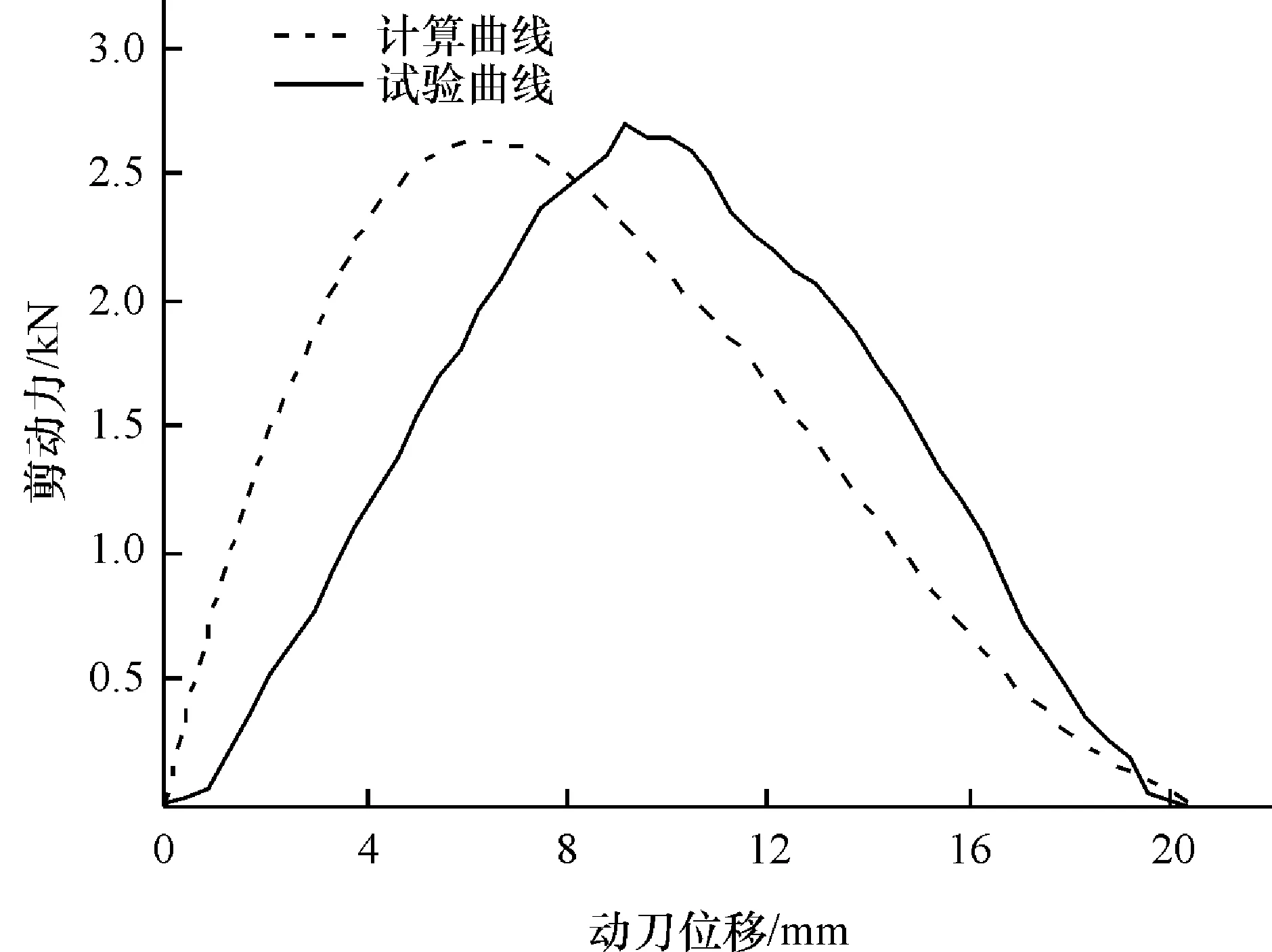
图8　刀片剪切力的计算结果与试验结果

Fig.8The comparison of calculating results with experimental results of the shearing force

动刀片剪切直径20 mm的树枝时，峰值剪切力计算值与试验值的相对误差小于4.6%，说明所建剪切力模型与实际情况比较接近。如果要进一步提高精度，可以考虑树枝受压后的整体变形及材料间层面的挤压变形。

3.3.2树枝含水率对峰值剪切力的影响图9为树枝直径d=15.3 mm、动刀刃角θ=20°、动刀剪切速度为250 mm·min-1时，峰值剪切力在树枝不同含水率条件下的计算数据与试验数据对比结果。结果表明，计算结果和试验结果的平均值具有相同的趋势，峰值剪切力计算值与试验平均值的相对误差小于5.7%。刀片峰值剪切力随含水率的升高而增大，树枝含水率(w)为78%时的刀片峰值剪切力约为含水率(w)50%时的1.1倍。

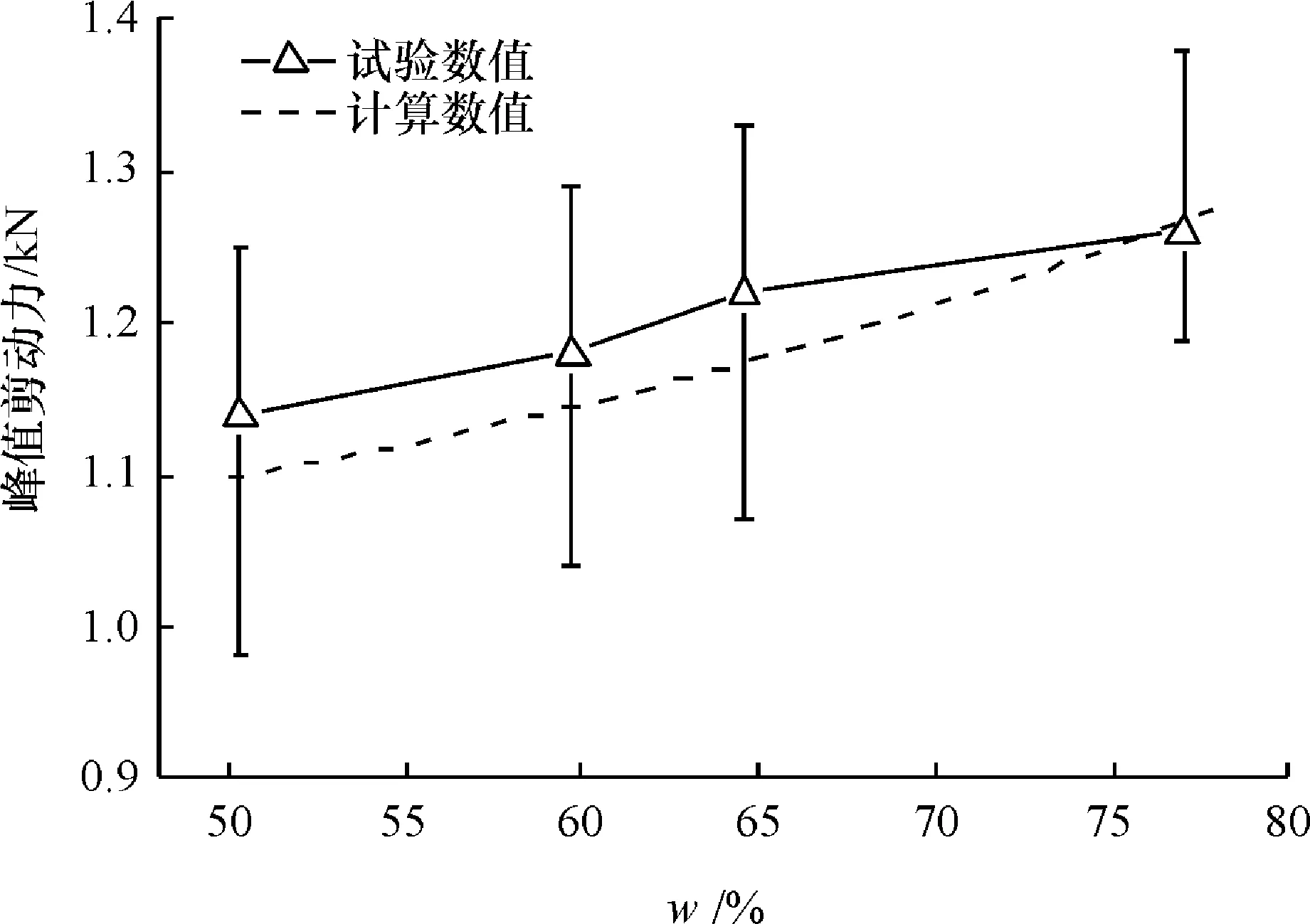
图9　含水率(w)对峰值剪切力的影响

3.3.3动刀片刃角对峰值剪切力的影响图10为树枝直径d=24.6 mm、含水率(w)为76%时，峰值剪切力在不同刃角条件下计算数据与试验数据的对比结果。结果表明，随着刀片刃角的增大，峰值剪切力显著增大，30°刃角时的刀片峰值剪切力约为10°刃角时的1.5倍，峰值剪切力计算值与试验平均值的相对误差小于4.1%。

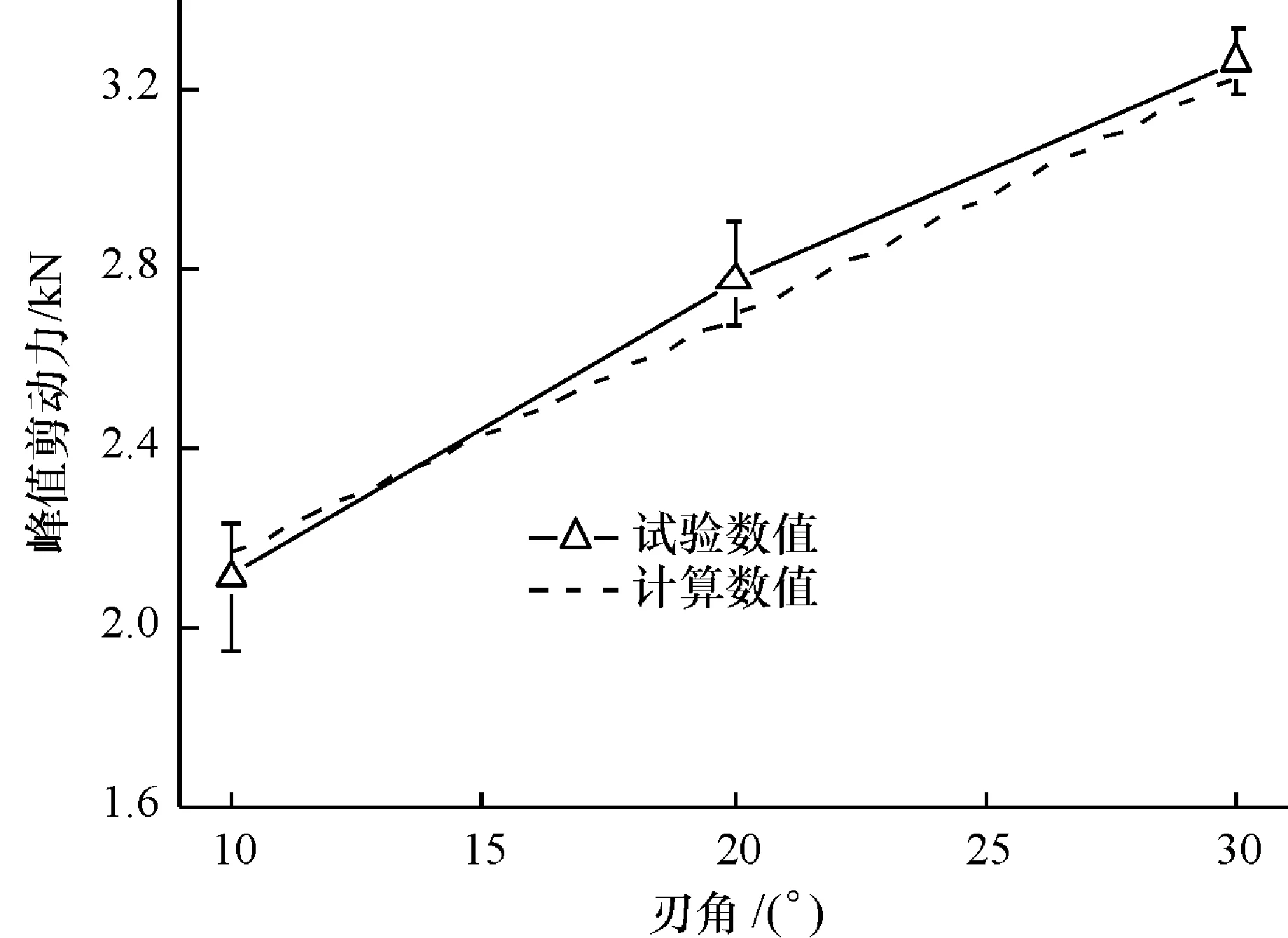
图10　刃角对峰值剪切力的影响

4结论

1)利用材料力学和弹性地基梁理论建立了树枝直刃剪切的数学模型，通过该模型可计算给定树枝直径、树枝含水率和刀片刃角条件下刀片剪切树枝所受剪切力的大小，通过该模型可以对刀片剪切力作出预测。

2)验证试验结果表明，动刀片剪切直径20 mm的树枝时，剪切力理论计算曲线与试验曲线趋势一致，峰值剪切力计算值与试验值的相对误差小于4.6%；当树枝含水率(w)为52%～78%时，刀片峰值剪切力随含水率升高而增大，树枝含水率(w)78%时的刀片峰值剪切力约为含水率(w)50%时的1.1倍，刀片峰值剪切力计算值与试验平均值的相对误差小于5.7%；当刀片刃角从10°逐渐增大到30°，峰值剪切力会显著增大，30°刃角时的刀片峰值剪切力约为10°刃角时的1.5倍，刀片峰值剪切力计算值与试验平均值的相对误差小于4.1%。

参考文献：

[1]刘权. 南方果树整形修剪大全[M]. 北京：中国农业出版社， 2000： 160-174.

[2]王慰祖，陆华忠，杨洲，等. 荔枝龙眼园机械化现状调查与分析[J]. 农机化研究， 2012， 34(3)： 237-241.

[3]吴良军，杨洲，汪刘一，等. 果树气动修剪机具研究与试验[C]∥学术委员会.国际农业工程大会论文集.北京：中国农业科技出版社， 2010： 187-191.

[4]吴良军，杨洲，段洁利，等. 龙眼树枝修剪机具刀片切割力的影响因素试验[J]. 农业工程学报，2012，28(24)： 8-14.

[5]吴良军，杨洲，洪添胜，等. 荔枝树枝力学特性的试验研究[J]. 农业工程学报， 2012， 28(16)： 68-73.

[6]吴良军，杨洲，王慰祖，等. 果树气动修剪机应用现状与发展趋势[J]. 现代农业装备， 2013(1)： 54-57.

[7]刘庆庭，区颖刚，卿上乐，等. 甘蔗茎秆切割力试验[J]. 农业工程学报， 2007， 23(7)： 90-94.

[8]刘庆庭，区颖刚，卿上乐，等. 甘蔗茎秆切割力的计算[J]. 农业机械学报， 2006， 37(9)：89-92.

[9]吴子岳，高焕文，张晋国，等. 玉米秸秆切断速度和切断功耗的试验研究[J]. 农业机械学报， 2001， 32(2)：38- 41.

[10]IGATHINATHANE C, WOMAC A R, SOKHANSANJ S. Corn stalk orientation effect on mechanical shearing[J]. Biosys Eng, 2010, 107(2): 97-106.

[11]AKRITIDIS C B. The mechanical characteristics of maize stalks in relation to the characteristics of shearing blade[J]. J Arg Eng Res, 1974, 19(1): 1-12.

[12]CHEN Y X, CHEN J, ZHANG Y F, et al. Effect of harvest date on shearing force of maize stems[J]. Livest Sci, 2007, 111(1/2): 33- 44.

[13]宗望远，黄小毛，徐爱英，等. 棉花幼苗茎秆弯曲及剪切性能试验[J]. 农业工程学报， 2012， 28(S2)： 118-124.

[14]YUMNAM J. Energetics of forage chopping[J]. AMA-Agr Mech Asia Af, 1991, 22(1): 59- 63.

[15]赵湛，李耀明，徐立章，等. 超级稻单茎秆切割力学性能试验[J]. 农业机械学报， 2010， 41(10)：72-75.

[16]MINNA P, TANJA H. The effects of different hand tool blade coatings on force demands when shearing wood[J]. Int J Ind Ergonom, 2003, 32(3): 139-146.

[17]CHATTOPADHYAY P S, PANDEY K P. Impact shearing behaviour of sorghum using a flail-cutter:A mathematical model and its experimental verification[J]. J Agr Eng Res, 2001, 78(4): 369-376.

[18]肖正福. 木材切削刀具学[M]. 哈尔滨：东北林业大学出版社， 1992： 1-28.

[19]黄义，何芳社. 弹性地基上的梁、板、壳[M]. 北京：科学出版社， 2005： 8-24.

[20]刘鸿文. 高等材料力学[M]. 北京：高等教育出版社，1984： 4-10.

[21]南京林产工业学院. 木材切削原理与刀具[M]. 北京： 中国林业出版社， 1983： 17-36.

[22]王慰祖，杨洲，张伟栋，等. 一种金属木材摩擦试验台：201110372183.6[P]. 2012- 04-25.

[23]中华人民共和国国家标准化管理委员会. 木材含水率测定方法：GB/T 1931—2009[S].北京：中国标准出版社， 2009.

[24]中华人民共和国国家标准化管理委员会. 木材顺纹抗拉强度试验方法：GB/T 1938—2009[S]. 北京：中国标准出版社， 2009.

[25]中华人民共和国国家标准化管理委员会.木材顺纹抗压强度试验方法：GB/T 1935—2009[S]. 北京：中国标准出版社， 2009.

[26]中华人民共和国国家标准化管理委员会.木材横纹抗压试验方法：GB/T 1939—2009[S]. 北京：中国标准出版社， 2009.

[27]徐友明. 木材学[M]. 北京：中国林业出版社， 2006：102-105.

[28]龙驭球. 弹性地基梁的计算[M]. 北京：人民教育出版社， 1981.

【责任编辑霍欢】

优先出版网址：http://www.cnki.net/kcms/detail/44.1110.s.20160601.1630.050.html

郭磊，张春红，胡钢.基于CE-Bézier曲面的拖拉机造型设计[J].华南农业大学学报，2016,37(4):112- 116.

Development and verification of a mathematical model of straight blade cutting longan branches

WANG Weizu1, WU Liangjun2, YANG Zhou1, LU Huazhong3, WANG Liuyi1, GUO Xiaoling1

(1 College of Engineering, South China Agricultural University, Guangzhou 510642, China;2 College of Automobile and Engineering Machinery, Guangdong Communication Polytechnic,Guangzhou 510650, China; 3 Guangzhou Academy of Agricultural Sciences, Guangzhou 510640, China)

Abstract：【Objective】To model the process of straight blade cutting longan branches based on material mechanics and elastic foundation beam theory, and to calculate the shearing force of branches from the straight blade cutting using the model. 【Method】Shixia longan branches were used as test materials. The mechanical parameters of the branches and the coefficient of friction between the branch and blade were measured using a universal material test machine and a custom friction tester. The peak shearing forces were measured by the universal material testing machine and also calculated by the developed model under conditions of different branch moisture contents (M), branch diameters (d) and blade bevel angles (θ). The blade used in the cutting tests had a bevel angle of 10°, 20° or 30°.【Result】When M=76%, d=20.4 mm and θ=20°, the calculated curve showed the same trend as the curve derived from the experimental results, and the error of the peak shearing force was around 2.3%. When d=15.3 mm, θ=20° and M >30% which was the fiber saturation point, the peak shearing force increased with the increment of M and calculated values were within the error ranges of the experimental data. When M=76%, d=24.6 mm and θ increased from 10° to 30°, the peak shearing force increased significantly and the calculated values were also within the error ranges of the experimental data.【Conclusion】The model can be used to estimate the shearing force and investigate the effects of different mechanical parameters on the peak shearing force. The results will provide theoretical reference for the design and optimization of pruning machines.

Key words：mathematical model; straight blade； shear; moisture content; bevel angle; longan branch;elastic foundation beam theory

收稿日期：2015- 11- 06优先出版时间：2016- 06- 01 2015- 12- 01优先出版时间：2016- 06- 01

作者简介：王慰祖(1979—)，男，副教授，博士，E-mail：egwwz@scau.edu.cn；通信作者：杨洲(1971—)，男，教授，博士，E-mail: yangzhou@scau.edu.cn 郭磊(1978—)，男，副教授，博士，E-mail: 79115521@qq.com

基金项目：广州市科技计划项目(2014J4100147)；现代农业产业技术体系建设专项(nycytx-32) 国家自然科学基金(51305344)；广东省教育教学成果奖培育项目(Z-SCG201406)；广东省高等学校优秀青年教师培养计划(Yq2013206)；中山市科技研究项目(2015B2356)

中图分类号：S776.274；S121

文献标志码：A

文章编号：1001- 411X(2016)04- 0105- 07

优先出版网址：http://www.cnki.net/kcms/detail/44.1110.s.20160601.1631.056.html

王慰祖，吴良军，杨洲， 等.树枝直刃剪切数学模型与试验[J].华南农业大学学报，2016,37(4):105- 111.