塑性铰区采用FRC柱试验研究及正截面承载力分析

秦玮琳，梁兴文

（1西安建筑科技大学土木工程学院，西安710055；2陕西同济土木建筑设计有限公司，西安710002）

塑性铰区采用FRC柱试验研究及正截面承载力分析

秦玮琳1，2，梁兴文1

（1西安建筑科技大学土木工程学院，西安710055；2陕西同济土木建筑设计有限公司，西安710002）

采用简化的纤维增强混凝土应力应变关系，根据截面变形的平截面假定和截面力的平衡方程，推导出塑性铰区采用纤维增强混凝土柱在不同极限状态时的曲率。根据各极限状态点曲率，求得截面上各分布力，对截面形心轴取距，到塑性铰区采用FRC柱的开裂、屈服、峰值和极限点的弯矩表达式。与试验结果对比表明，计算值与试验值吻合较好。

纤维增强混凝土；钢筋混凝土柱；曲率；弯矩；拟静力试验

历次震害表明，钢筋混凝土柱承受压、弯、剪的复合作用，柱端部常产生严重破坏，甚至引起结构整体倒塌。为此，中国抗震规范要求钢筋混凝土柱端部箍筋加密，并根据结构抗震等级，确定箍筋加密区长度和箍筋的最小直径、最大间距。同时，学者们进行了大量的试验研究和理论分析，提出一些改进措施，如采用高强混凝土、高强箍筋或改善箍筋形式等［1-5］。但工程实践证明，过密的柱端箍筋间距、复杂的箍筋形式极易造成柱混凝土浇筑质量问题，进而影响柱的性能。因此，提高混凝土柱抗震性能的方法需兼顾施工简便。

纤维增强混凝土（Fiber Reinforced Concrete，简称FRC）是一种高韧性的混凝土，研究表明［6-10］：FRC有超高的受拉应变硬化性能，可用于以受剪为主的构件和高剪应力作用下的受弯构件；FRC增大了受弯和受剪构件的受剪强度、变形能力和损伤容限；有很大的受压应变能力，可减少或取消抗震构件的约束钢筋数量，方便施工；将FRC用于钢筋混凝土柱下端局部区域［11］，可显著改善其抗震性能。研究塑性铰区采用FRC柱的抗震性能和正截面承载力计算，具有重要的理论意义和实用价值。

文献［12］根据近年来高强混凝土的研究成果，提出了高强混凝土正截面承载力计算用的受压应力应变曲线，根据该曲线运用《混凝土结构设计规范》（GBJ 10—89）的正截面承载力计算方法分析了高强混凝土构件的正截面承载力，建议了应力应变曲线参数的取值。笔者在钢筋混凝土柱的预期损伤部位（潜在的塑性铰区）采用纤维增强混凝土，完成了9根FRC柱试件和1根钢筋混凝土柱对比试件的拟静力试验，分析了试件的破坏形态，并记录了试件特征点（开裂荷载点、屈服荷载点、峰值荷载点和极限荷载点）处的荷载值。根据截面几何条件和平衡条件，推导出FRC柱各特征点处的正截面受弯承载力计算公式，并与试验值进行对比分析，结果表明，建议的FRC柱正截面受弯承载力计算公式计算结果与试验结果吻合较好。

1 试验概况

1.1 试件设计

设计了9根柱，试件编号为FRC1～FRC9，截面尺寸均为250 mm×250 mm；柱底部FRC区高度均为300 mm，且伸入底梁100 mm；各柱的纵向钢筋相同，均为416，屈服强度为440 MPa，极限强度为609 MPa；箍筋为Φ6＠100，屈服强度为273 MPa，极限强度为427 MPa。同时制作了一根普通混凝土柱RC10试件作为对比试件。

除柱下部局部范围采用FRC外，柱的其余部分和底梁均采用普通混凝土。各试件的编号、剪跨比、FRC或混凝土立方体抗压强度、轴压比等具体参数见表1。试件尺寸及配筋详图如图1所示，图中阴影部分为FRC材料，h表示柱加载点高度。

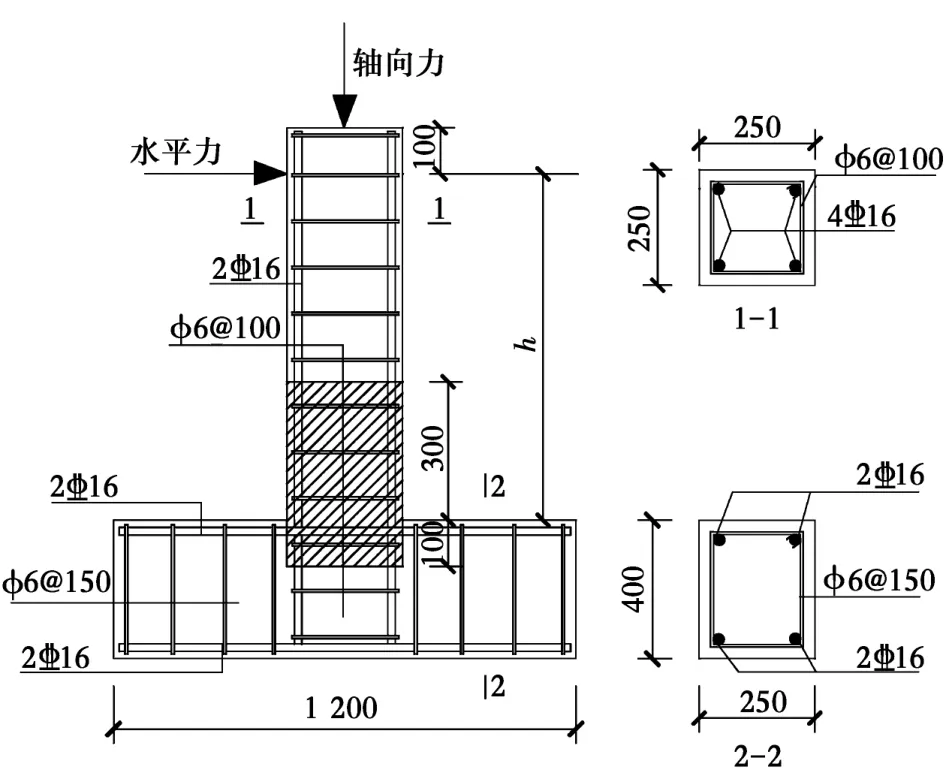
图1 试件尺寸及配筋图Fig.1 Cross section and reinforcement details of specimens

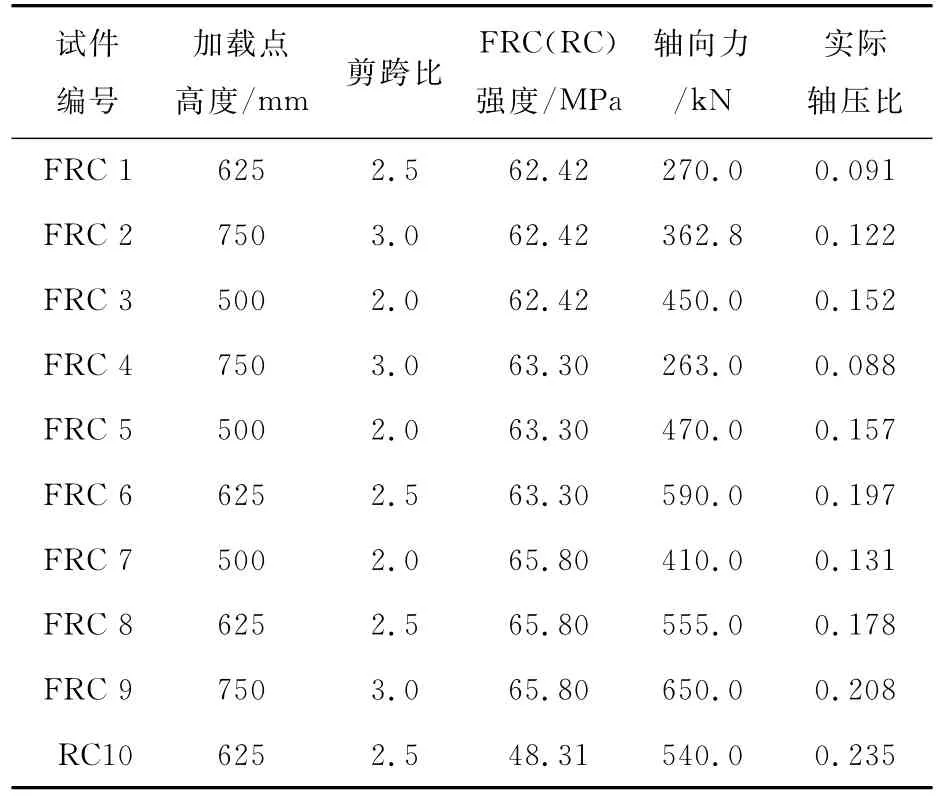
表1 试件参数Table 1 Parameters of specimens

1.2 试验装置和加载制度

试验时，首先用竖向油压千斤顶施加轴向荷载并在试验过程中保持不变，然后施加反复水平荷载。水平荷载采用荷载位移混合控制方法，试件屈服前按荷载控制，正、反向加载、卸载各1次，直至试件屈服。随后进入位移控制循环，控制位移取为屈服位移的倍数，每一控制位移下循环3次，直至水平荷载显著降低（小于峰值荷载的85%）或试件不能稳定地承受轴向荷载时，停止试验。试件加载装置如图2所示，加载制度如图3所示。加载过程中主要测试的内容有：水平荷载、水平位移、纵向钢筋应变、箍筋应变以及试件的竖向变形。所有测试数据用TDS-602数据采集仪采集。

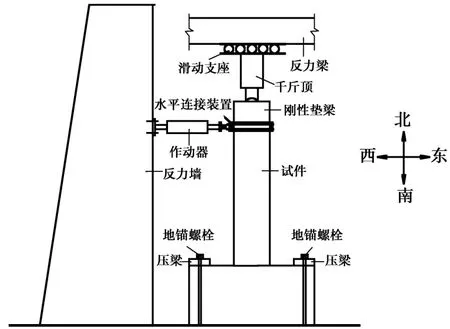
图2 加载装置示意图Fig.2 Sketch of loading device

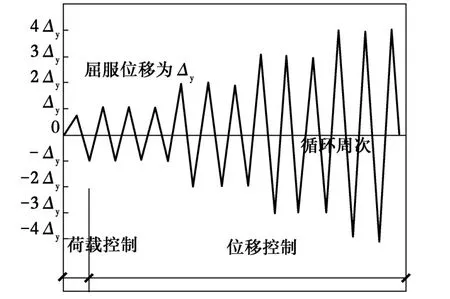
图3 加载制度示意图Fig.3 Loading program

1.3 试验结果分析

1.3.1 试验现象分析 试件加载后，第一条裂缝为水平方向的微裂缝，出现在柱根部，此后随着继续加载，柱根部10 cm长的水平裂缝发展至多条。继续加载，作动器记录的PΔ曲线斜率明显降低，此时柱纵筋屈服，构件屈服。此时柱底部的主裂缝已经形成，且不断地变宽和延长，柱底部高15～30 cm范围内出现斜裂缝。继续加载至峰值荷载，柱底部主裂缝基本贯通，其余水平裂缝不发展延伸，柱底部高15～30 cm范围内斜裂缝延伸，加载时不断地发出“吱吱”的纤维破坏声音，试件处于弹塑性状态。继续加载至极限荷载，柱底部贯通裂缝（个别试件主裂缝未贯通）不断变宽，斜裂缝缓慢发展，角部FRC外鼓甚至脱落，纵筋外部FRC出现竖向裂缝，和角部FRC外鼓混合作用，出现个别的角部FRC外鼓掉落现象，“吱吱”的纤维破坏声剧烈，表现出显著的破坏征兆，试件处于弹塑性状态。继续加载，柱底部主裂缝继续变宽，“吱吱”声剧烈，个别纵筋断裂，柱的水平承载力迅速降低，试件破坏。各试件的破坏形态如图4所示。

9根不同轴压比、剪跨比和FRC强度的FRC柱试件，其破坏都是以柱底部水平裂缝不断变宽、纵筋屈服为标志的，这属于典型的弯曲破坏。破坏前角部FRC外鼓，纤维破坏的“吱吱”声剧烈，有明显的征兆，属于延性破坏。与RC柱相比，塑性铰区裂缝开展更多，角部FRC压碎现象不明显只有外鼓，易于震后修复。

图4 试件破坏形态图Fig.4 Failure patterns of specimens

根据试验记录的水平力及其作用位置的水平位移，绘制了10个试件实测的水平荷载位移滞回曲线，如图5所示。图中上、下横坐标分别表示柱顶点位移角θ和顶点水平位移Δ，纵坐标F代表水平荷载；红色点分别代表开裂点、屈服点、峰值点、极限点与破坏点的位置。其中与开裂点、屈服点、峰值点和极限点相应的位移试验值见表2。

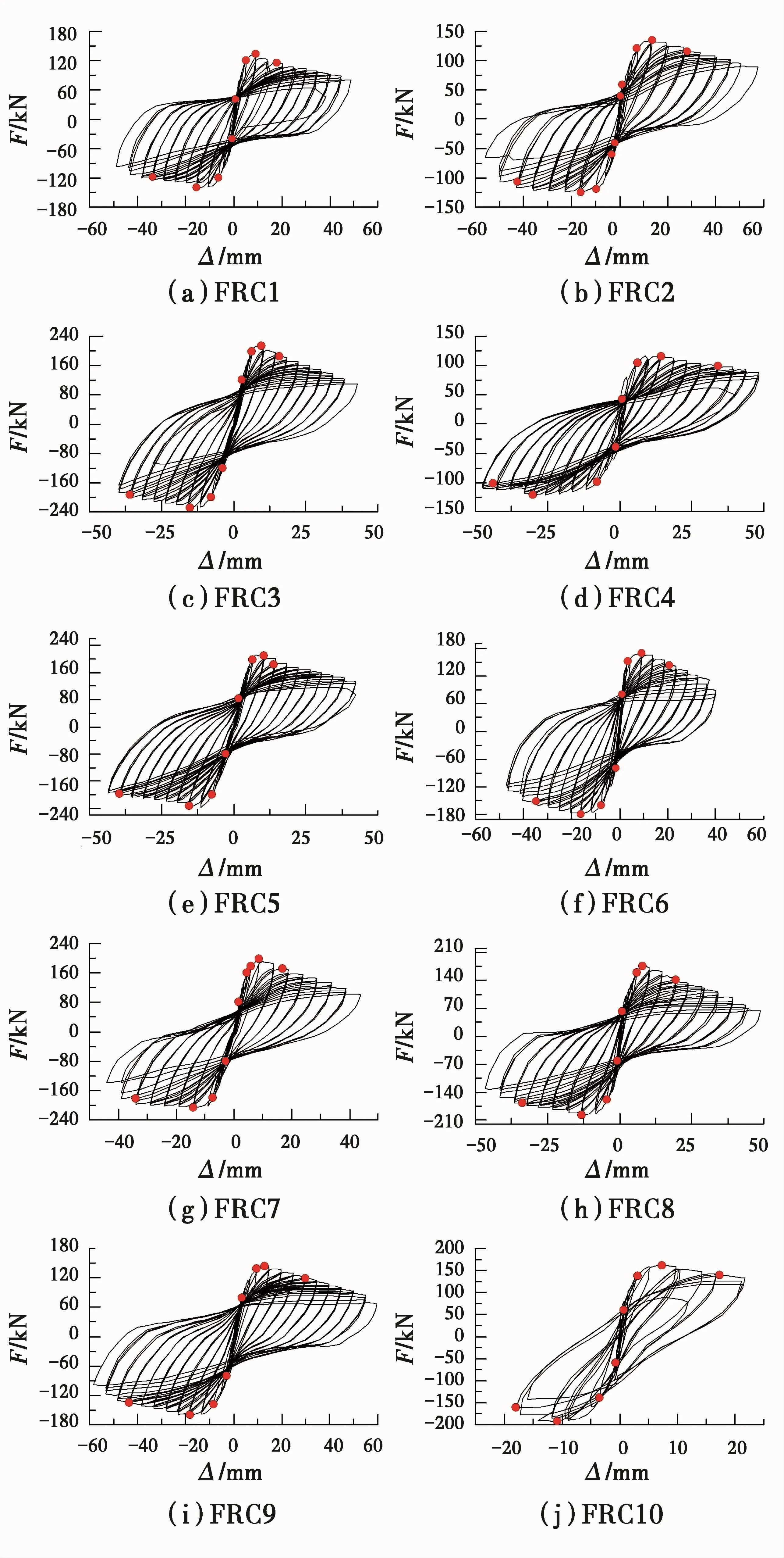
图5 荷载位移滞回曲线Fig.5 Hysteretic curves of specimens

1.3.2 纵筋应变分析 纵筋应变通过应变片由应变系统自动采集，可方便观察加载过程中纵筋应变变化情况。由试验现象和纵筋应变数据可知，二者变化情况基本一致。以试件FRC2为例，详细说明纵筋应变变化情况。在加载初期，柱底截面弯矩较小，纵筋应变处于弹性阶段；随着柱底截面弯矩的增加，纵筋应变逐渐加大，柱端屈服时，纵筋应变达到1 809με；达到峰值弯矩时，纵筋应变达到2 234με；试件达到极限弯矩时，纵筋应变片破坏。由此可知，由纵筋应变变化情况可预测柱截面弯矩及试件破坏情况。

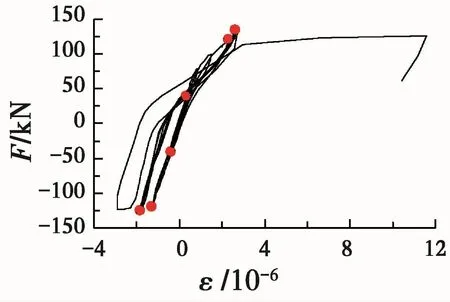
图6 柱底截面纵筋变化情况Fig.6 Situation of longitudinal reinforcement at column bottom

2 正截面承载力分析

2.1 基本假定

1）平截面假定适用于本文的弯矩计算；

2）受压区FRC及混凝土在柱屈服前均保持线性应力应变关系；

3）FRC单轴受拉本构采用双折线模型［13］，如图7所示；混凝土受拉本构模型按《混凝土结构设计规范》采用；

4）钢筋采用理想弹塑性本构关系。

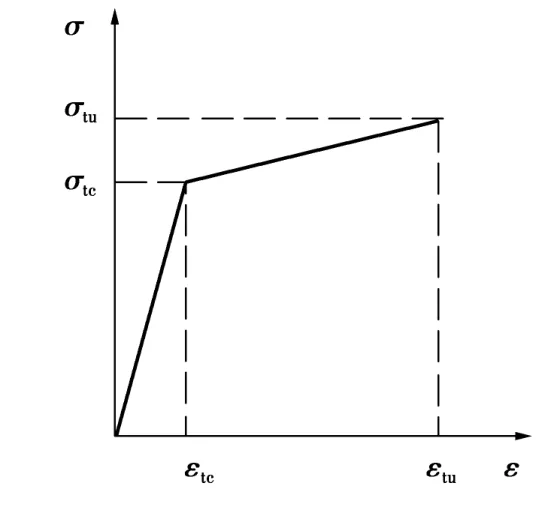
图7 FRC拉伸应力应变曲线Fig.7 Stress strain diagram for the tensile FRC

2.2 开裂弯矩计算

柱底截面受拉区边缘应变达到混凝土或FRC的极限拉应变时，柱达到开裂极限状态。此时，受拉区混凝土或FRC出现塑性，应力为曲线分布，受压区应力基本为线性分布，截面应力、应变图如图8所示。

为简化计算，可按开裂弯矩相等的原则，将截面受拉区的曲线应力图形转换为三角形线性分布。假定混凝土或FRC的最大拉应变达到2倍轴心受拉峰值应变时截面即将开裂，则由即将开裂截面应变分布图可得截面的开裂曲率由截面力的平衡条件可得

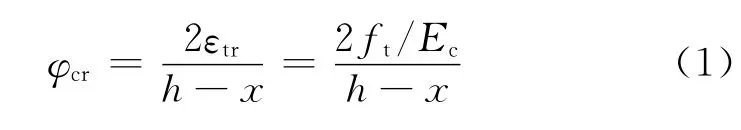
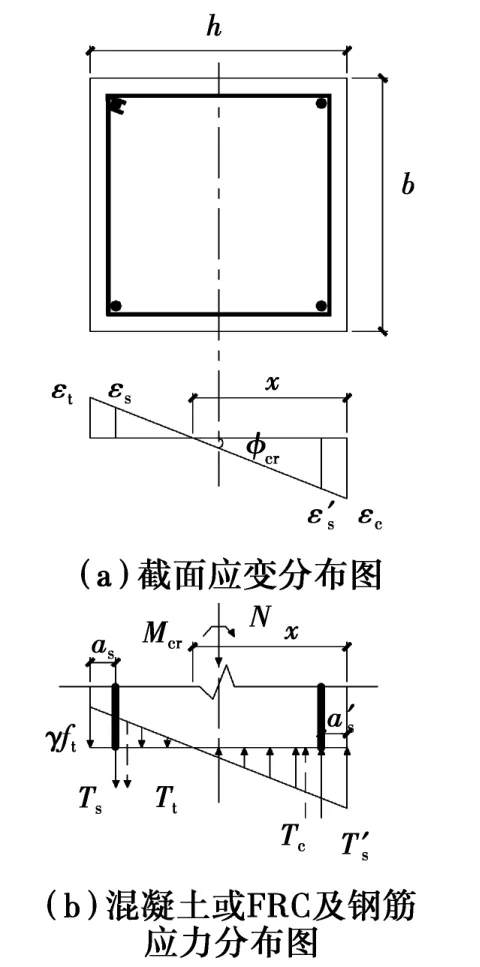
图8 开裂状态截面应力、应变图Fig.8 Stress strain diagram at crack load point

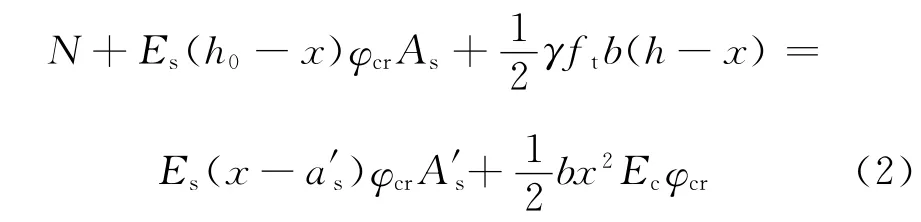
联立式（1）、（2）解得受压区高度x［14］。对截面形心轴取矩可得混凝土柱或FRC柱开裂弯矩表达式

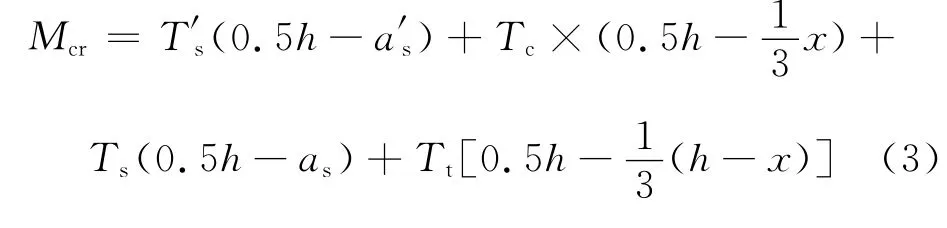
式中：γ为混凝土或FRC构件的截面抵抗矩塑性影响系数；εtr为混凝土或FRC的峰值应变；ft为混凝土或FRC的轴心抗拉强度；Ec为混凝土或FRC的弹性模量；h0为截面有效高度；Es为钢筋的弹性模量；As为截面受拉钢筋面积；a′s为受压纵筋重心到截面受压边缘的距离；A′s为截面受压钢筋面积；b为截面宽度；N为截面承受的轴力；T′s纵向受压钢筋合力，T′s＝Es（x－a′s）φcrA′s；Ts为纵向受拉钢筋合力，Ts＝Es（h0－x）φcrAs；Tc受压区混凝土或FRC的合力，为受拉区混凝土或FRC的合力，

2.3 屈服弯矩计算

柱底截面受拉区纵向受力钢筋应变达到钢筋屈服应变时，柱达到屈服极限状态。FRC柱分析时考虑截面受拉区FRC的受拉作用，截面应力、应变分布如图9所示，钢筋混凝土柱分析时忽略受拉区混凝土受拉作用。

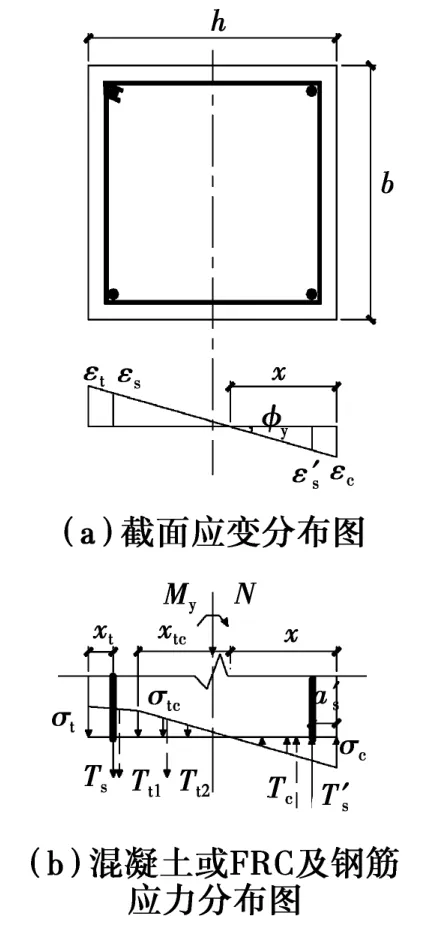
图9 屈服状态截面应力、应变图Fig.9 Stress strain diagram at yield load point

由平截面假定及截面应变分布图可得截面的屈服曲率，即

用εt表示FRC的拉应变，εtu表示FRC的极限拉应变。若εt＜εtu，则xt＝0，表示截面受拉区FRC均承受拉力。由平截面假定可得受压钢筋的应变以及受压区混凝土的边缘压应变，则根据截面力的平衡方程可得

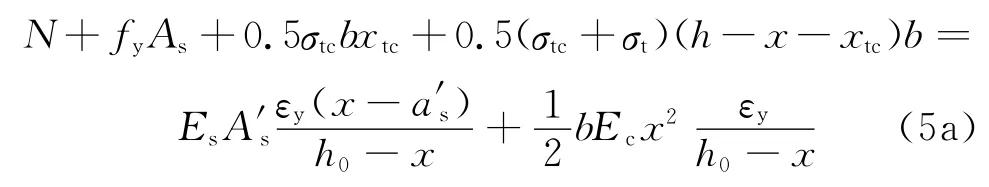
联立式（4）和式（5a）可解得x和φy，对截面形心轴取矩可得屈服弯矩表达式

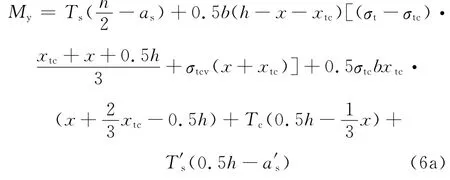
若εt≥εtu，则。由平截面假定可得受压钢筋的应变以及受压区FRC的边缘压应变，则根据截面力的平衡方程可得

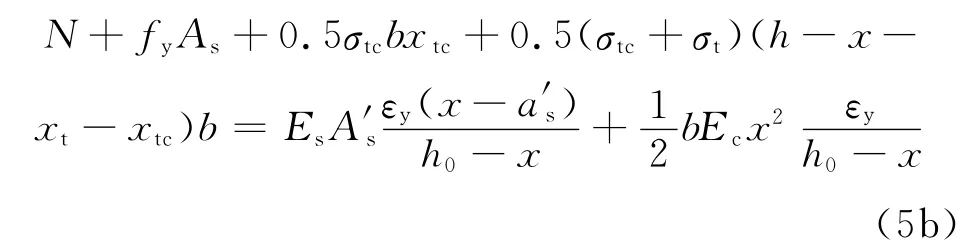
联立式（4）、式（5b）可解得x和φy，对截面形心轴取矩可得屈服弯矩表达式：

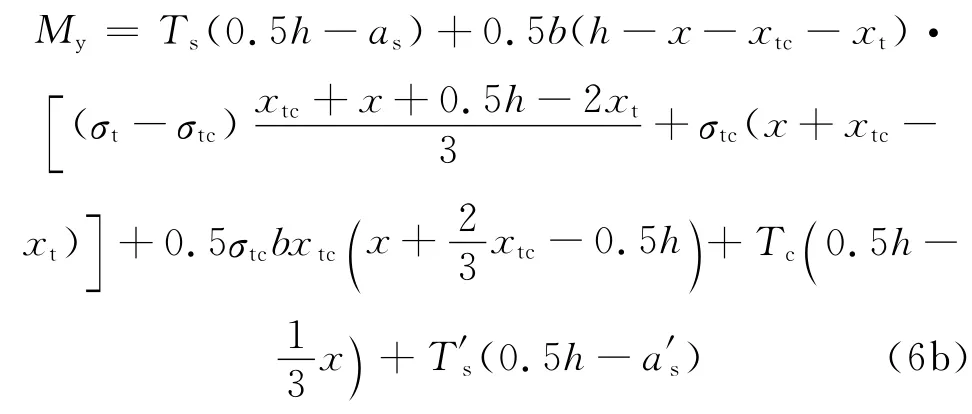
对于普通钢筋混凝土柱不考虑混凝土受拉作用，对形心轴取矩可得屈服弯矩表达式

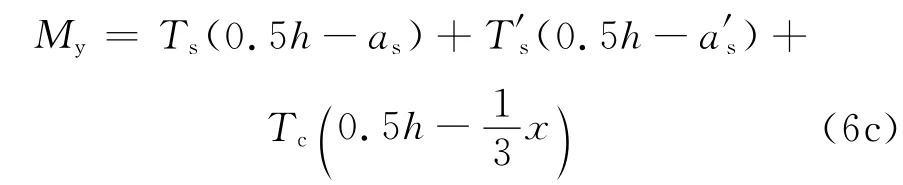
式中：εy为钢筋的屈服应变；ε′s为受拉钢筋的应变，取（x－a′s）φy；εc为截面受压区边缘FRC压应变，取xφy；σtc为FRC开裂应力；σt为截面受拉区边缘FRC拉应力（εt≥εtu时，σt＝σtu；εt＜εtu时，σt＝；xt为假定退出工作的FRC沿截面高度；xtc为三角形分布受拉区高度，取；截面上各应力的合力分别为：

2.4 峰值弯矩计算

根据试验结果，柱发生大偏心受压破坏，则柱底截面受压区边缘混凝土或FRC的应变达到极限压应变时，柱底截面达到最大承载能力，由平截面假定可得此时截面曲率

式中：εcu为混凝土或FRC的极限压应变，对混凝土取0.003 3；对FRC取0.007 46［13］。

对于普通混凝土及下端采用FRC的柱，分析时均不考虑受拉混凝土或受拉FRC的作用，弯曲破坏时受拉、受压纵筋均屈服，计算截面混凝土或FRC的压力时，用等效矩形应力图代替实际的混凝土或FRC压应力图形，截面应力、应变分布如图10所示，则由截面力的平衡方程可得

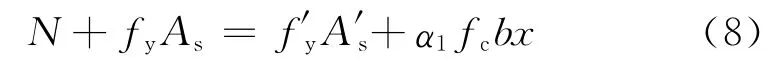
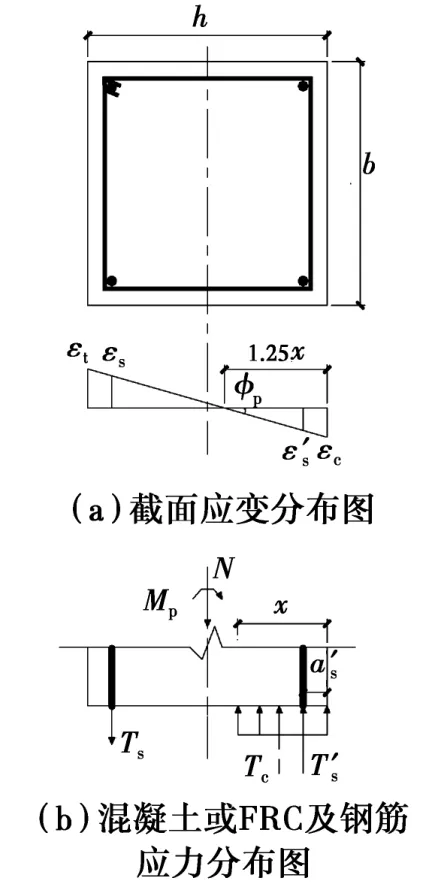
图10 峰值状态截面应力、应变图Fig.10 Stress strain diagram at peak load point

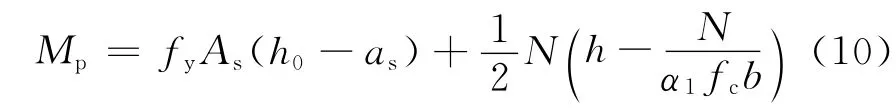
2.5 极限弯矩计算

对于钢筋混凝土柱或FRC，极限弯矩Mu取0.85倍的峰值弯矩

2.6 试验验证

根据试验结果，对提出的FRC柱正截面受弯承载力计算公式进行验证，开裂点、屈服点和峰值点受弯承载力见表2。

由表2可知：1）开裂点、屈服点和峰值点的正截面受弯承载力试验值和计算值比值的平均值分别为0.95、0.95和1.31，变异系数分别为0.10、0.06和0.08，计算值和试验值吻合较好，本文所给出的FRC柱正截面受弯承载力计算公式具有较高的计

联立式（7）、式（8）可解得x和φp。对截面形心轴取矩，可得峰值弯矩

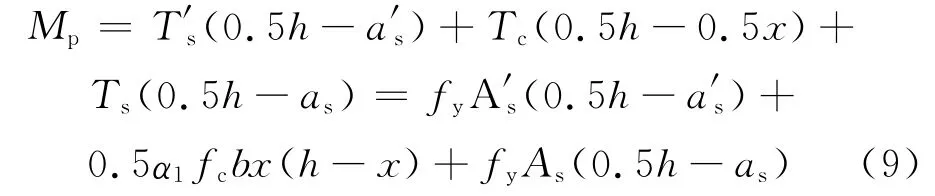
式中：α1、β1表示与等效矩形应力图有关的系数，按规范［15］取值。

在截面对称配筋的情况下，由式（8）和（9）可得算精度；2）峰值点处受弯承载力试验值偏大于计算值，计算结果偏于安全。

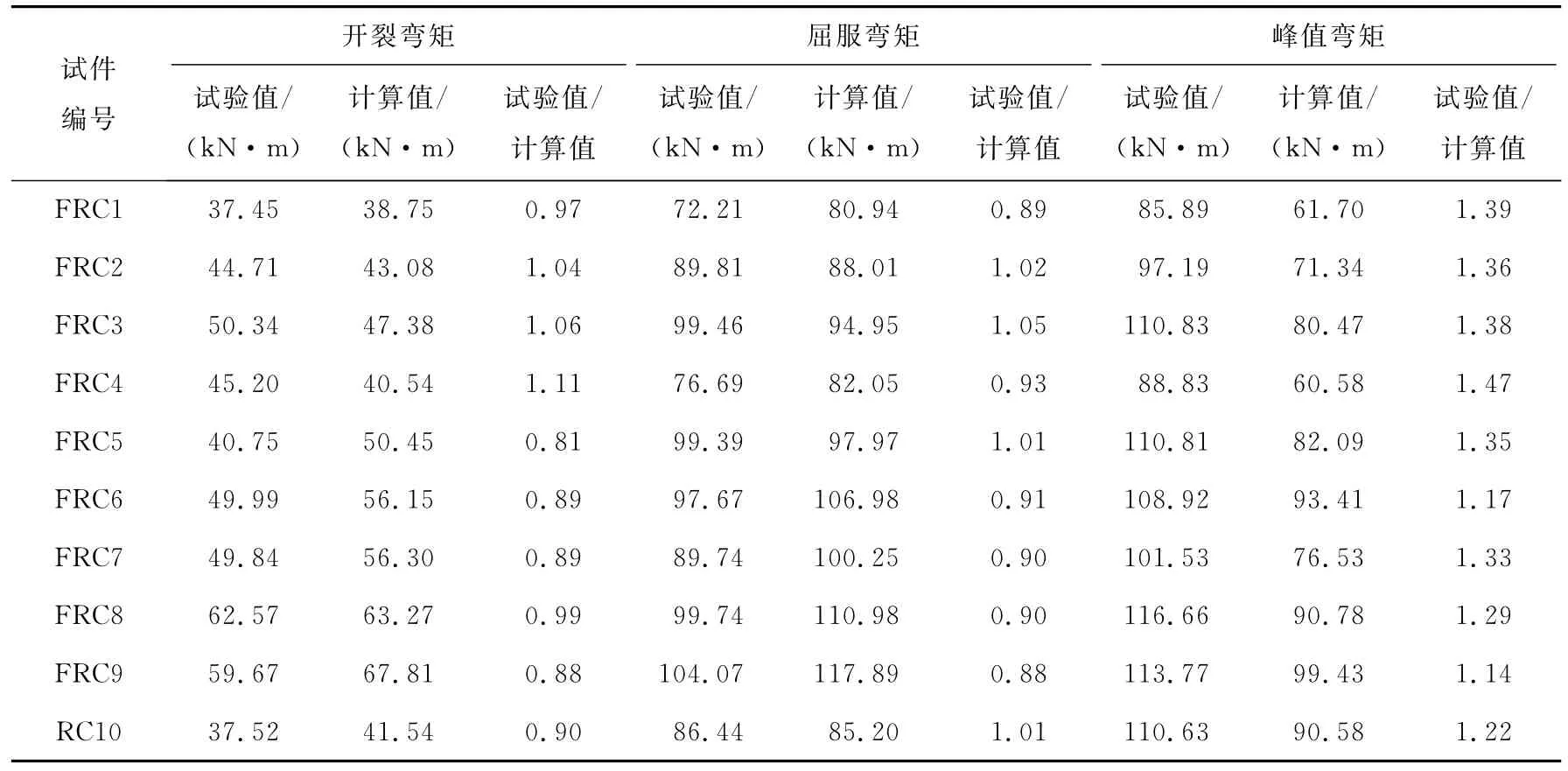
表2 柱正截面受弯承载力计算值和试验值的比较Table 2 Comparison of experimental and prediction for normal scetion bearing capacity in columns

3 结 论

1）柱试验破坏时，FRC柱仅角部FRC外鼓、开裂，而钢筋混凝土柱角部混凝土已经压碎，FRC柱震后易于修复。

2）经FRC6、FRC8和RC10试件对比可知，在小轴压比情况下，FRC柱的开裂弯矩可提高33%～66%，屈服弯矩可提高13%～15%，峰值和极限弯矩基本不变。

3）对FRC采用简化应力应变关系，开裂、屈服状态时考虑受拉区FRC的拉应力，峰值、极限状态时均不考虑FRC拉应力，根据平截面假定和截面力的平衡方程，联立方程求得各状态点截面的曲率，根据曲率求得截面上各分布力，对截面形心轴取距可得弯矩表达式。通过与试验结果比较，可以看出建议公式具有较好的准确性，可用于计算开裂、屈服、峰值和极限点的弯矩承载力。

［1］Bechtoula H，Mehani Y，Kibboua A，et al.Seismic behavior of high strength reinforced concrete columns under reversed cyclic loading［C］／／the World Conference on Earthquake Engineering，2012：24-28.

［2］王全风，沈章春，杨新勇，等.HRB400级钢筋混凝土短柱抗震性能试验研究［J］.建筑结构学报，2008，29（2）：114-117.

Wang Q F，Shen Z C，Yang X Y，et al.Seismic behavior of HRB400 reinforcement concrete columns［J］.Journal of Building Structures，2008，29（2）：114-117.（in Chinese）

［3］杨坤，史庆轩，赵均海.高强箍筋高强混凝土柱的塑性铰长度［J］.工程力学，2013，30（2）：1-6.

Yang K，Shi Q X，Zhao J H.Plastic hinge length of high-strength concrete columns confined by highstrength stirrups［J］.Engineering Mechanics，2013，30（2）：1-6.（in Chinese）

［4］李青宁，郑先超，颜志勇，等.高强螺旋箍筋约束混凝土柱连接抗震性能试验研究与理论分析［J］.建筑结构学报，2013，34（8）：1-10.

Li Q N，Zheng X C，Yan Z Y，et al.Seismic behavior experimental study and theoretical analysis on highstrength spiral stirrups confined concrete column［J］.Journal of Building Structures，2013，34（8）：1-10.（in Chinese）

［5］姜睿，徐世烺，贾金青.高轴压比PVA纤维超高强混凝土短柱延性的试验研究［J］.土木工程学报，2007，40（8）：54-60.

Jiang R，Xu S L，Jia J Q.An experimental study on the seismic ductility of PVA fiber supper-high-strength concrete columns with high axial load ratios［J］.China Civil Engineering Journal，2007，40（8）：54-60.（in Chinese）

［6］李艳，梁兴文，刘泽军.PVA纤维增强水泥基复合材料：性能与设计［J］.混凝土，2009（12）：54-57.

Li Y，Liang X W，Liu Z J.PVA fiber reinforced cementitious composites：performance and design［J］.Concrete，2009（12）：54-57.（in Chinese）

［7］Fischer G，Li V C.Deformation behavior of fiber reinforced polymer reinforced engineered cementitious composite（ECC）flexural members under reversed cyclic loading conditions［J］.ACI Structural Journal，2003，100（1）：25-35.

［8］Li V C，Wang S，Wu C.Tensile strain-hardening behavior of polyvinyl alcohol engineered cementitious composite（PVA-ECC）［J］.ACI Material Journal，2001，98（6）：483-492.

［9］Li V C.On engineered cementitious composites（ECC）：A review of the material and its applications［J］.Journal of Advanced Concrete Technology，2003，1（3）：215-230.

［10］Parra-Montesinos G J.High-performance fiber reinforced cement composites：An alternative for seismic design of structures［J］.ACI Structural Journal，2005，102（5）：668-675.

［11］梁兴文，康力，车佳玲，等.局部采用纤维增强混凝土柱的抗震性能试验与分析［J］.工程力学，2013，30（9）：243-250.

Liang X W，Kang L，Che J L，et al.Experiments and analyses of seismic behavior of columns with fiberreinforced concrete in bottom region［J］.Engineering Mechanics，2013，30（9）：243-250.（in Chinese）

［12］叶列平，庄崖屏，吴佩刚，等.高强混凝土构件正截面承载力计算方法［J］.土木工程学报，2000，33（6），70-75.

Ye L P，Zhuang Y P，Wu P G.et al.The capacity of normal section for high-strength concrete members［J］.China Civil Engineering Journal，2000，33（6），70-75.（in Chinese）

［13］李艳.高性能纤维增强水泥基复合材料的力学性能研究［D］.西安：西安建筑科技大学，2011.

Li Y.Study on mechanical performance of high performance fiber reinforced cement composite［D］.Xi′an：Xi′an University of Architecture and Technology，2011.（in Chinese）

［14］秦玮琳，梁兴文，徐洁，等.塑性铰区采用纤维增强混凝土柱变形能力计算方法研究［J］.建筑结构，2015，45（20）：63-68.

Qin W L，Liang X W，Xu J，et al.Study on calculation method for deformation capacity of reinforced concrete columns with fiber reinforced concrete in plastic hinge region［J］.Building Structure，2015，45（20）：63-68.（in Chinese）

［15］GB 50010—2010混凝土结构设计规范［S］.北京：中国建筑工业出版社，2010：42-43.

GB 50010—2010 Code for design of concrete structures［S］.Beijing：China Architecture＆Building Press，2010：42-43.（in Chinese）

（编辑 胡英奎）

Experimental analysis of normal section bearing capacity for reinforced concrete columns with fiber reinforced concrete in plastic hinge region

Qin Weilin1，2，Liang Xingwen1

（1.School of Civil Engineering，Xi′an University of Architecture and Technology，Xi′an 710055，P.R.China；2.Shaanxi Tongji Architectural Design Civil Engineering Co.Ltd，Xi′an 710002，P.R.China）

Based on simplified stress-strain relationship of fiber reinforced concrete and the plane section assumption and equilibrium equation，the curvature of reinforced concrete columns with fiber reinforced concrete in plastic hinge region under different ultimate state was derived.Then，the distribution force in the cross section was obtained by calculating the curvature under different ultimate states.By taking the distance of the cross section centroid axis，the moment expressions of reinforced concrete columns with fiber reinforced concrete in plastic hinge region at crack load point，yield load point，peak load point and ultimate load point were attained.The calculated values agree well with the experimental results.

fiber reinforced concrete；reinforced concrete columns；curvature；bending moment；quasi static test

2015-05-12

National Natural Science Foundation of China（No.51278402，51078305）

TU375.3

A

1674-4764（2016）01-0084-08

10.11835／j.issn.1674-4764.2016.01.012

2015-05-12

国家自然科学基金（51278402、51078305）

秦玮琳（1987-），男，主要从事高层建筑结构及抗震研究，（E-mail）13228060426.com＠163.com。

梁兴文（通信作者），男，教授，博士生导师，（E-mail）liangxingwen2000＠163.com。

Author brief：Qin Weilin（1987-），main research interest：structures of tall building and seismic research，（E-mail）13228060426.com＠163.com.

Liang Xingwen（corresponding author），professor，doctor supervisor，（E-mail）liangxingwen2000＠163.com.