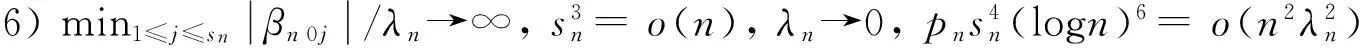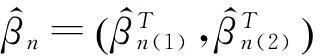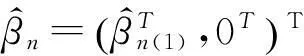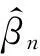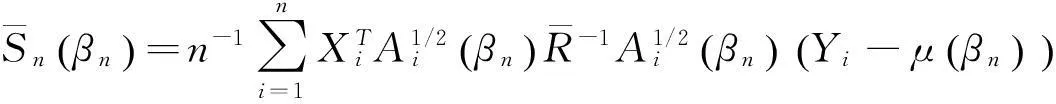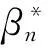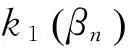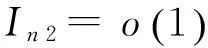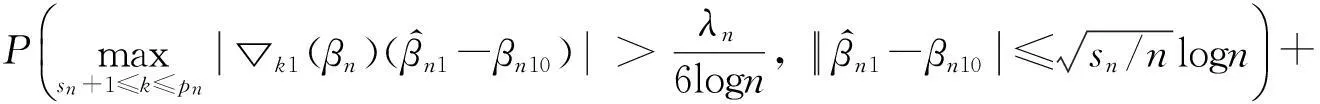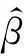高维纵向计数数据的惩罚广义估计方程分析

尹长明，苏连菊，蒙建国

(广西大学 数学与信息科学学院，南宁　530004)



高维纵向计数数据的惩罚广义估计方程分析

尹长明，苏连菊，蒙建国

(广西大学 数学与信息科学学院，南宁530004)

摘要：已有文献对连续性的高维纵向数据的研究较多,而对离散高维纵向数据的研究较少，且条件较复杂。在较简单的条件下，证明了分析高维纵向计数数据的惩罚广义估计方程估计的存在性、相合性与渐近正态性。

关键词：计数数据；惩罚广义估计方程; 高维纵向数据; 渐近正态性

计数数据在物理学、地质学、生物学、金融和可靠性理论等领域都有广泛的应用。已有文献对连续性的高维纵向数据的研究较多,而对离散的高维纵向数据研究较少，特别是对高维纵向计数数据的研究较少,且条件较复杂[1-7]。

设在试验中对第i个个体的第j次观测，得到响应变量Yij和pn×1维协变量Xij，其中i=1,2,…,n,j=1,2,…,m。设来自不同个体的观测值相互独立，来自相同个体则是相关的。Yij服从Poisson分布， 令期望

(1)

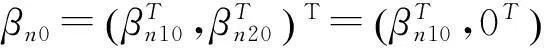
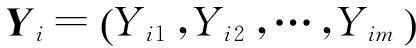
(2)

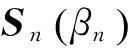
(3)

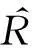
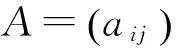
文献[3]用惩罚广义估计方程研究了高维纵向数据，在较复杂条件得到了估计的渐近性质。本文简化了条件，得到如下结果：

定理假设以下条件成立：

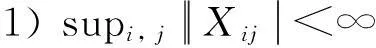
2) 未知参数βn属于紧子集B⊆Rpn，真正的参数值是集合B的内点；

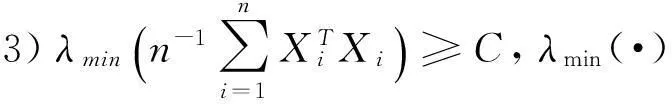
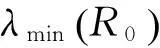
5)C

(4)

(5)

(6)

且对任意单位向量αn∈Rsn有

(7)

其中

2定理的证明

(8)

可通过证明式(9)、(10)来证明式(8)：

由假定1)、4)、5)、6)和Markov不等式，可得式(9)左边小于

因而式(9)成立。

下面先证式(10)。由Taylor 展开式得

(11)

注意到

由Berstein’s inequality[8]得

因此，由假定6)得

(12)

其中

再由文献[2]定理3.6知

(13)

由假定1)、4)、5) 、6)和Markov不等式得

同理证得In22=ο(1),In23=ο(1)，从而In2=ο(1)。

最后，可证In3=ο(1)。 由假定1)、4)、5)、6)和式(13)，可得

参考文献：

[1]FAHRMEIR L,TUTZ F.Multivariate statistcal modelling based on generalized linear models[M].New York:Springer-Verlag,1994.

[2]WANG L.GEE annalsis of clustered binary data with diverging number of covariates[J].Annals of Statistics,2011,39(1):389-417.

[3]WANG L,ZHOU J,QU A.Penalized Generalized Estimating Equations for High‐Dimensional Longitudinal Data Analysis[J].Biometrics,2012,68(2):353-360.

[4]FAHRMEIR L,KAUFMANN H.Consistency and asymptotic normality of the maximum likelihood estimator in generalized linear models [J].Annals of Statistics,1985,13:342-368.

[5]LIANG K Y,ZEGER S L.Longitudinal data analysis using generalized linear models[J].Biometrika.1986,73(1):13-22.

[6]XIE M,YANG Y.Asymptotics for generalized estimating equations with large cluster sizes[J].The Annals of Statistics,2003,31(1):310-347.

[7]BALAN R M,SCHIOPU-KRATINA I.Asymptotic results with generalized estimating equations for longitudinal data[J].The Annals of Statistics,2005,33(2):522-541.

[8]VAN D V A,WELLNER J.Weak Convergence and Empirical Processes:with applications to statistics[M].NewYork:Springer-Verlag,1996.

(责任编辑陈艳)

Analysis of Penalized Generalized Estimating Equations for High-Dimensional Longitudinal Count Data

YIN Chang-ming, SU Lian-ju, MENG Jian-guo

(College of Mathematics and Information Science, Guangxi University, Nanning 530004, China)

Abstract:There is a lot of research on the high dimensional continuous longitudinal data in the literature, however, the research on the discrete high dimensional longitudinal data is less, and the condition is more complicated. In this paper, under the weaker conditions, it proved the existence, consistency and asymptotic normality of the estimators of the penalized generalized estimating equations for the high-dimensional longitudinal count data.

Key words：count data; penalized generalized estimating equations; high-dimensional longitudinal data; asymptotic normality

收稿日期：2016-02-22

基金项目：国家自然科学基金资助项目(11061002);广西自然科学基金资助项目(2015GXNSFAA139006)

作者简介：尹长明( 1966—)，男，湖北人， 博士， 教授，主要从事广义线性模型、属性数据的研究。

doi:10.3969/j.issn.1674-8425(z).2016.06.026

中图分类号：O175

文献标识码：A

文章编号：1674-8425(2016)06-0154-05

引用格式：尹长明,苏连菊,蒙建国.高维纵向计数数据的惩罚广义估计方程分析[J].重庆理工大学学报(自然科学)，2016(6):154-158.

Citation format：YIN Chang-ming, SU Lian-ju, MENG Jian-guo.Analysis of Penalized Generalized Estimating Equations for High-Dimensional Longitudinal Count Data [J].Journal of Chongqing University of Technology(Natural Science)，2016(6):154-158.