Mn掺杂对FeAl材料力学性能影响的第一性原理研究
王 芬, 郑义兵,2
(1.陕西科技大学 材料科学与工程学院,陕西 西安 710021;2.许昌电气职业学院,河南 许昌 461000)
Mn掺杂对FeAl材料力学性能影响的第一性原理研究
王芬1, 郑义兵1,2
(1.陕西科技大学 材料科学与工程学院,陕西 西安710021;2.许昌电气职业学院,河南 许昌461000)
摘要:为了研究第三元素Mn 的掺杂对B2型FeAl 力学性能的影响,采用基于密度泛函理论(density functional theory,DFT)广义梯度近似(generalized gradient approximation,GGA)的第一性原理方法,在对超晶胞优化的基础上,对Mn原子可能置换的Fe和Al原子分别进行了形成焓的计算,确定了Mn原子容易置换Al原子.接着进行了弹性常数的计算,获得了FeAl-Mn的弹性常数C11、C12和C44的值(C11= 305.06 GPa,C12= 145.76 GPa和C44=132.32 GPa)并判断该体系是机械稳定的.通过Voigt-Reuss-Hill(VRH)近似,进一步得到了体积模量B、剪切模量G、杨氏模量E、泊松比v及B/G的值(B=198.86 GPa,G=107.95 GPa,E=274.22 GPa,v=0.27,B/G=1.84).最后,通过能带结构、态密度、布居分析及差分电荷密度对Mn掺杂FeAl的增强机理进行了详细分析.得出了Mn的固溶增加了原子间电荷转移量、参与了杂化、增强了结合能力、提高了FeAl的稳定性等结论.
关键词:第一性原理;FeAl金属间化合物;置换固溶;弹性常数;电子结构
0引言
B2型FeAl的优点诸如高硬度、低密度、出色的抗氧化、耐腐蚀[1,2]等使其有希望成为新一代的中高温结构材料并能替代不锈钢.但其在室温下脆性大和超过600 ℃后强度急剧下降、抗蠕变性能变差的缺点[3]限制了其大规模工业应用.
在过去的数十年里,研究者从理论和实验两方面对固溶合金元素改善FeAl材料的性能进行了广泛的研究[4-8],尤其是在材料性能计算方面取得了长足发展.赵荣达等[9]利用第一性原理进行的研究发现,稀土元素La、Ac、Sc 和 Y的加入可以改善FeAl的脆性.陈煜等[10]用第一性原理研究了Cr、 Mo 和 W对FeAl电子结构和力学性能的影响,得出了3种元素中Mo的添加对FeAl的增韧效果最好、提高了机械稳定性等结论.Guillermo H.Bozzolo等[11]用Bozzolo-Ferrante-Smith (BFS)方法研究了合金元素三元添加FeAl、NiAl等B2合金的优先占位情况,发现Ti、V、Cr、W、Zr、Hf和Ta倾向于置换Al,而Ni、Si和Ru则容易替换Fe.N.I.Medvedeva等[12]用local density linear muffin-tin orbital(LMTO)方法研究了第三元素单独添加对于FeAl的固溶强化,表明La、 Zr、Mo、 Ti、V 和Cr易于置换Al原子,三元添加强化的机理在于原子的尺寸差异、弱化化学键等.但这些研究对于Mn掺杂对FeAl增强的微观理论研究还很有限.因此,本文采用基于密度泛函理论广义梯度近似的第一性原理方法,研究了合金元素Mn的加入对FeAl力学性能的影响及其机理,对固溶强化后的电子结构进行了分析,从微观角度揭示了Mn元素对FeAl 的影响机制.
1晶体结构和计算方法
B2型FeAl属于空间点群为pm-3m (NO.221) 的立方晶系结构,晶胞中包含1个Fe原子和1个Al原子.Fe原子和Al原子分别占据1a(0,0,0)和1b(0.5,0.5,0.5)位置.晶格参数为a=b=c=2.909Å[3].本文采用包含16个原子的2×2×2超晶胞进行研究,如图1(a)所示.图1(b)为1个Mn原子置换Al原子时超晶胞的结构图.文中用FeAl及FeAl-Mn表示铁铝超晶胞及Mn掺杂后的超晶胞.为了方便分析,第2部分在计算形成焓及进行布居分析时采用 Fe8Al8来表示FeAl超晶胞,用Fe8Al7Mn表示Mn原子置换Al原子之后的超晶胞,用Fe7Al8Mn表示Mn原子置换Fe原子之后的超晶胞.
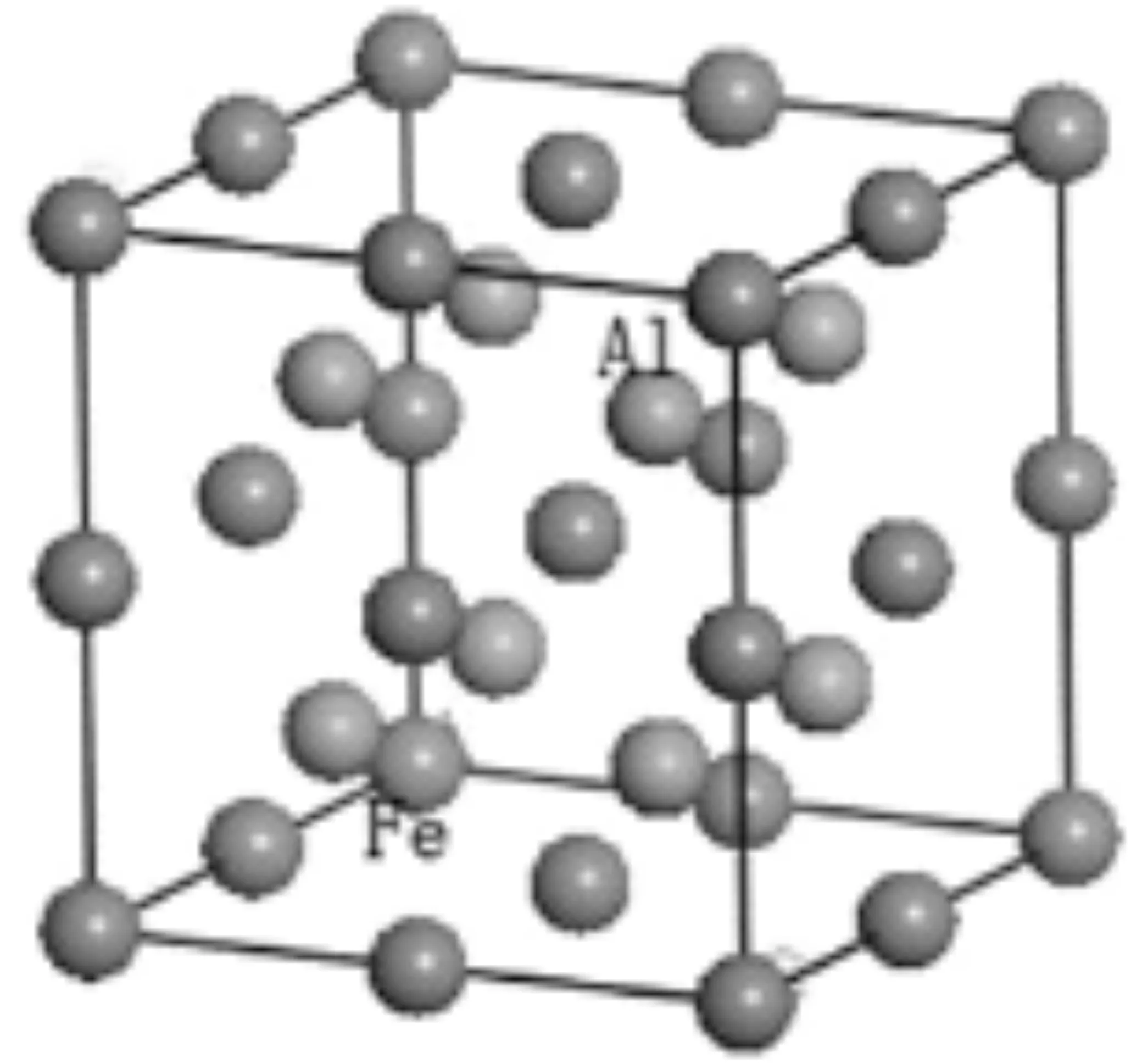
(a)FeAl超晶胞

(b)FeAl-Mn超晶胞图1 FeAl和FeAl-Mn的超晶胞模型
计算采用基于密度泛函理论平面波赝势方法[13-15]的CASTEP(Cambridge Serial Total Energy Package)软件包,使用广义梯度近似(generalized gradient approximation,GGA)的Perdew-Burke-Eruzerhof (PBE)算法[16]来描述交换关联能.平面截断能为350.0 eV,使用Monkhorst-Pack方案[17]在第一布里渊区8×8×8k点的网格上进行能量计算.使用密度混合[18]的Pulay方案和有限基设置矫正[19]来评估能量和压力.采用Broyden-Fletcher-Goldfarb-Shanno(BFGS)技术[20]对所有原子的位置进行弛豫以获得最小的结构能.几何优化的收敛条件如下:总能量收敛值为5.0×10-6eV/atom,每个原子的受力小于0.01 eV/Å,应力偏差小于0.02 GPa,最大公差偏移小于5.0 ×10-4Å,SCF收敛能量为1.0×10-6eV/atom.除此之外,考虑到Fe有磁性,计算中设置了电子自旋.
2结果与讨论
2.1晶格参数和稳定性
对FeAl和FeAl-Mn超晶胞几何优化之后,由最小总能量所得的晶格常数为:LFeAl=5.706,LFeAl-Mn=5.682.其中计算所得的LFeAl接近实验值5.818[3],偏差为1.899%,在采用赝势的正常误差范围1%~2%之内.表明文中所选的计算参数是合适的.
FeAl-Mn的热力学稳定性通过形成焓ΔH的计算来反映,具体的计算公式如式(1)[21]所示.
NAlEAl(atom)+NMnEMn(atom))]
(1)
式(1)中:Etotal是固溶体的总能量;EFe(atom)、EAl(atom)、EMn(atom)、 表示Fe、Al、Mn的原子能量;NFe、NAl、NX分别是Fe、Al、Mn原子的个数.用EFe7Al8Mn、EFe8Al7Mn分别表示Fe原子和Al原子被Mn原子置换之后的化合物Fe7Al8Mn和Fe8Al7Mn的总能量.EFe、EAl分别表示由公式(1)计算得到的Fe7Al8Mn和Fe8Al7Mn的形成焓.Esite为替代形成焓,计算公式如式(2)所示.
Esite=EFe-EAl
(2)
如果Esite>0,Mn原子将优先取代Al原子.反之,Mn原子将优先取代Fe原子.
计算结果:EFe7Al8Mn=-7 167.85 eV,EFe8Al7Mn=-7 976.61 eV,EFe=-6.90 eV,EAl=-7.25 eV,Esite=0.35 eV.故Mn原子将优先置换Al原子,这与文献[12]中的计算结果也是一致的.
2.2弹性常数和力学性能
固体的弹性常数作为力学和动态特性的链接,起到重要的作用,并且提供材料刚度和稳定性的重要信息.文中,弹性常数Cij通过应力应变方法得到,并通过广义胡克定律来描述,如式(3)[22]所示.
(3)
式(3)中:{σi}代表应力;{εj}代表应变;[Cij]是弹性常数矩阵C的元素.对于立方晶系,C为6×6的矩阵,具体如式(4)[23]所示.
(4)
如公式(4)所示,矩阵C里有3个独立的弹性常数(C11、C12和C44),计算结果为:C11= 305.06 GPa,C12=145.76 GPa和C4=132.32 GPa.利用弹性常数的计算结果,可以判断立方晶体结构的机械平衡,条件如式(5)[24]所示.
C11>0,C44>0,C11+2C12>0,
C11>C12,C11>B>C12
(5)
带入验证发现FeAl-Mn体系满足条件,其在基态下是机械稳定的.
利用弹性常数C11、C12和C44的计算结果,通过Voigt-Reuss-Hill(VRH)[25]近似,可以得到体积模量B、剪切模量G、杨氏模量E以及泊松比v.对于立方晶系,具体的计算公式如式(6)~(11)所示.
(6)
(7)
(8)
(9)
(10)
(11)
在外部压力为0 GPa时的计算结果为:B=198.86 GPa,G=107.95 GPa,E=274.22 GPa,v=0.27,B/G=1.84.根据Pugh准则[26],体积模量B和剪切模量G的比值B/G可以作为判断材料是脆性或者延性的条件.如果B/G大于1.75,则这种材料为延性,否则为脆性.此外,如果泊松比v大于0.26,则材料为延性,否则也为脆性.基于以上两个条件判断,可以发现FeAl-Mn体系为延性.这意味着Mn的加入,改善了FeAl的本征脆性.
2.3电子结构
能带结构和态密度用于描述固溶Mn元素的增强机理.图2为FeAl(图2(a))和FeAl-Mn(图2(b))在布里渊区沿着高对称方向的能带结构图.图中的水平虚线表示费米能级(EF),并且价带穿过费米能级进入导带,这暗示着在费米能级附近存在自由电子.结合图3中的分波态密度,能够发现FeAl的自由电子主要来源于Fe-3d和Al-3p轨道,FeAl-Mn的自由电子主要来源于Fe-3d、Al-3p 和Mn-3d轨道.此外,FeAl-Mn在费米能级附近能带的数目明显多于FeAl,这意味着Mn的置换固溶增加了FeAl金属键的强度,也就相当于弱化了FeAl中的共价键,从而增加了FeAl的机械稳定性.
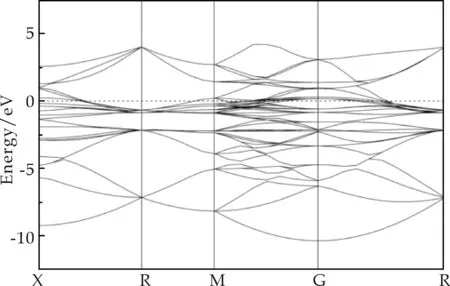
(a)FeAl的能带结构图

(b)FeAl-Mn的能带结构图图2 FeAl和FeAl-Mn的能带结构图
图3展示了FeAl(图3 (a))和FeAl-Mn(图3(b))的总态密度(Total Density of States,TDOS)和分波态密度(Partial Density of States,PDOS),可以反映能带结构中电子态的特定组成.PDOS还可以使原子对于每个能带的贡献归结到特定的原子轨道.图中,垂直的虚线表示费米能级(EF),并且可以发现TDOS中的费米能级是非零的,这表示FeAl金属间化合物整体上呈现了金属的特点.图3(a)中,成键峰(-4.0~2.7 eV)主要是来自于Fe-3d轨道电子的贡献,但FeAl电子结构的主要特性是由Fe-3d和Al-3p轨道电子的杂化决定的.图3(b)显示键合不仅仅来自于Fe-3d和Al-3p轨道的电子,而且Mn-3d轨道的电子也参与了杂化.由此,可以得出结论:Mn的掺杂增强了FeAl的结合能力.
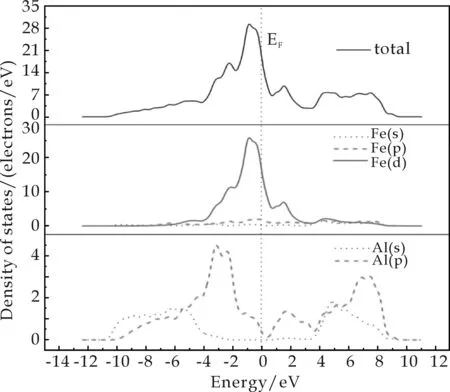
(a)FeAl的TDOS和PDOS
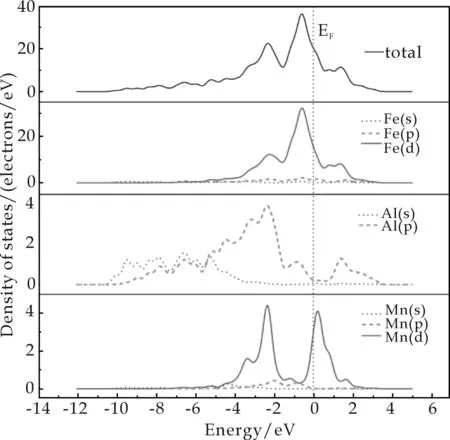
(b)FeAl-Mn的TDOS和PDOS图3 FeAl、 FeAl-Mn的TDOS和PDOS
布居分析能够提供关于化学键合定量的结果和更有深度的信息,以便于确定一些状态特性.Mulliken布居分析的结果如表1和表2所示.表1为FeAl超晶胞的Mulliken布居分析结果.从表1中可以看到,FeAl超晶胞中Fe原子和Al原子之间存在电荷转移,也即Al原子失去电荷,总量为1.12(0.14×8),而Fe原子得到Al原子失去的电荷.经过Mn元素的合金化后,电荷转移总量为1.36(0.17×8),比合金化前的电荷转移增加了0.24.各原子之间电荷转移情况表明,Mn加入后,Fe与4个Al原子之间的电荷转移总量略微减少(0.08),与3个Al原子之间的电荷转移总量则增加了0.03,而与Mn的电荷转移量则很大(0.41).这表明Mn的加入,增强了Fe-Mn间金属键作用,减弱了Fe-Al之间的共价键作用.这就是Mn对FeAl脆性有所改善的微观结构原因.表3为FeAl和FeAl-Mn晶胞里最近邻的键长和键布居的计算结果.文献[27]表明,键布居值的正、负分别表示处于键合和反键合状态.并且,键布居值的高、低分别暗示着化学键展现强烈的共价键合或者离子键合.由此可知,Al-Al和 Fe-Al键处于键合状态,而Fe-Mn、Al-Mn和Fe-Fe处于反键合状态.Al-Mn键的数值为负但接近为0,暗示虽然其处于反键化状态,但Al原子和Mn原子之间没有强烈的相互作用.同理,FeAl超晶胞里的Fe-Al键作用类似.综合键布居分析的结果可以发现,FeAl里起主要作用的是Fe-Fe键和Al-Al键,FeAl-Mn里起主要作用的是Fe-Mn、Al-Al、Fe-Al和Fe-Fe键.

表1 Fe8Al8的Mulliken电子布居
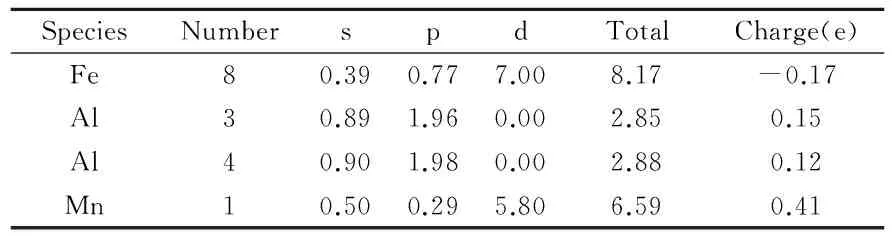
表2 Fe8Al7Mn的Mulliken 电子布居
表3FeAl和FeAl-Mn的键长(Å)和键布居

SpeciesBondlengthFe-FeFe-AlFe-MnAl-MnAl-AlBondpopulationFe-FeFe-AlFe-MnAl-MnAl-AlFeAl2.8532.471——2.853-0.200.09——0.21FeAl-Mn2.8032.4502.4282.8412.841-0.120.14-0.38-0.070.30

图4 FeAl和FeAl-Mn的差分电荷密度图
差分电荷密度能进一步说明成键特征.图4给出了FeAl和FeAl-Mn沿着(110)平面的差分电荷密度图.标尺中的密度范围为-0.5180 e/Å3到0.3484 e/Å3,红色和蓝色分别表示电荷密度的增加和减少.如图4(a)中所示,Fe原子和Al原子的电子云没有重叠,并且Fe-Fe之间的电子密度值高于Al-Al 和Fe-Al,这表明Fe-Fe键强于Al-Al键和Fe-Al键.从图4(b)中可以发现,Fe原子和Mn原子之间的电子密度明显高于图4(a)中Fe原子和Al原子之间的电子密度.表明Mn的掺杂增强了原子间的结合力从而提高了FeAl的机械稳定性.并且,Fe原子和Mn原子之间的电子云发生了一定程度的畸变,Mn原子周围电荷的重新分布展示出一种纺锤形的蓝色内核和围绕着的四片淡红色的花瓣.Mn原子的特殊形状及其很强的键角特点源于不同元素之间的电负性差[28],这种键角特点有可能导致延展性的降低.
3结论
通过第一性原理对Mn掺杂FeAl的计算与分析,可以得出如下结论:
(1)Mn原子容易置换Al原子.
(2)对力学相关模量的计算显示,Mn的加入改善了FeAl本征脆性(B/G=1.84,v=0.27),均大于判断条件(B/G>1.75,v>0.26),并符合机械稳定的条件.
(3)Mn固溶之后,其3d轨道的电子也参与了FeAl成键的杂化,增强了原子间的结合能力.
(4)Mn元素的微合金化,增加了原子间电荷的转移量(从1.12增加到1.36),削弱了原子间的共价键作用,从而提高了FeAl的稳定性.
参考文献
[1] Z.Liu,W.Gao,F.Wang.Oxidation behaviour of FeAl Interme-tallic coatings produced by magnetron sputter deposition[J].Scr.Mater,1998,39(11):1 497-1 502.
[2] M.Rudy,G.Sauthoff.Dislocation creep in the ordere Interme-tallic (Fe,Ni) Al phase[J].Mater.Sci.Eng,1986,81(8):525-530.
[3] 孙康宁,尹衍升,李爱民.金属间化合物/陶瓷基复合材料[M].北京:中国机械工业出版社,2002.
[4] C.T.Liu,E.P.George,P.J.Maziasz,et al.Recent adva- nces in B2 iron aluminide alloys:Deformation,fracture and alloy design[J].Mater.Sci.Eng.A,1998,258(12):84-98.
[5] David Colas,Anna Fraczkiewicz,FrancoisLouchet.Nickel in-nduced strengthening of boron-doped FeAl (B2) alloys[J].Intermetallics,2007,15(1):85-92.
[6] T.L.Lin,Dingqiang L i,Yi Liu.Superplasticity in large grained FeAl-based intermetallic alloys[J].Intermetallics,1998,6(4):243- 256.
[7] R.S.Sundar,S.C.Deevi.High-temperature strength and creep resistance of FeAl[J].Mater.Sci.Eng.A,2003,357(9):124-133.
[8] M Eumann,M Palm,G Sauthoff.Alloys based on Fe3Al or FeAl with strengthening Mo3Al precipitates[J].Intermetallics,2004,12(6):625-633.
[9] 赵荣达,朱景川,刘勇,等.FeAl(B2)合金La、Ac、Sc和Y元素微合金化的第一性原理研究[J].物理学报,2012,61(13):137 102-137 107.
[10] 陈煜,姚正军,张平则,等.Cr、 Mo和W对FeAl金属间化合物电子结构和力学性能影响的第一性原理研究[J].稀有金属材料与工程,2014,43(9):2 112-2 117.
[11] Guillermo H.Bozzolo,Ronald D.Noebe,Carlos Amador.Site occupancy of ternary additions to B2 alloys[J].Intermetallics,2002,10(2):149-159.
[12] N.I.Medvedeva,YU.N.Gornostyrev,D.L.Novikov,et al.Ternary site preference energies,size misfits and solid solution hardening in NiAl and FeAl[J].Acta mater,1998,46(10):3 433-3 442.
[13] M.Pang,Y.Zhan,H.Wang,et al.Ab initio study of AlCu2M (M=Sc,Ti and Cr) ternary compounds under pressures[J].Comput.Mater.Sci.,2011,50(10):2 930-2 937.
[14] M.D.Segall,P.J.D.Lindan,M.J.Probert,et al.First principles simulation:Ideas,illustrations and the CASTEP code[J].J.Phys.Condens.Matter,2002,14(11):2 717.
[15] D.Vanderbilt.Soft self-consistent pseudopotentials in a generalized eigenvalue formalism[J].Phys.Rev.,B,1990,41(12):7 892-7 899.
[16] J.P.Perdew,K.Burke,M.Ernzerhof.Generalized gradient approximation made simple[J].Phys.Rev.Lett.,1996,77(6):3 865-3 870.
[17] H.J.Monkhorst.Hartree-fock density of states for extended systems[J].Phys.Rev.B,1979,20(4):1 504-1 510.
[18] H.J.Monkhorst,J.D.Pack.Special points for brillouin zone integrations[J].Phys.Rev.B,1976,13(12):5 188-5 195.
[19] G.P.Francis,M.C.Payne.Finite basis set corrections to total energy pseudopotential calculations[J].J.Phys.Condens Matter,1990,2(5):4 395-4 401.
[20] B.Hammer,L.B.Hansen,J.K.Norkov.Payne.Improved adsorption energetics within density-functional theory using revised perdew-burke-ernzerhof functionals[J].Phys.Rev.,B,1999,59(11):7 413-7 419.
[21] B.R.Sahu.Electronic structure and bonding of ultralight LiMg[J].Mater.Sci.Eng.B,1997,49(1):74-78.
[22] V.B.Deyirmenjian,V.Heine,M.C.Payne,et al.Ab initio at-omistic simulation of the strength of defective aluminum and tests of empirical force models[J].Phys.Rev.B,1995,52(21):15 191-15 198.
[23] J.F.Nye.Physical properties of crystals[M].Oxford:Oxford University Press,1985.
[24] Y.Pan,W.M.Guan,K.H.Zhang.First-principles calculation of the phase stability and elastic properties of ZrPt compounds at ground state[J].Physica B,2013,427(10):17-21.
[25] R.Hill.The elastic behavior of a crystalline aggregate[J].Proc Phys.Soc.Sect.A,1952,65(3):349-352.
[26] S.F.Pugh.Xcii.Relations between the elastic moduli and the plastic properties of polycrystalline pure metals[J].Philos-Mag,1954,45(3):823-843.
[27] Y.Cao,J.C.Zhu,Y.Liu,et al.First-principles studies of the structural,elastic,electronic and thermal properties of Ni3Si[J].Comput.Mater.Sci.,2013,69(3):40-45.
[28] J.Hafner.Charge-density analysis of bonding in Laves phases[J].J.Phys.F:Met.Phys.,1985,15(3):1 879-1 886.
【责任编辑:蒋亚儒】
The first-principles study on the effect of mechanical properties and mechanism on account of the Mn doping on the FeAl
WANG Fen1, ZHENG Yi-bing1,2
(1.School of Materials Science and Engineering, Shaanxi University of Science & Technology, Xi′an 710021, China; 2.Xuchang Electric Vocational College, Xuchang 461000, China)
Abstract:In order to study the effect on the mechanical behavior of B2 type FeAl on account of doping the third element Mn,and chosen the first principles method which based on the generalized gradient approximation(GGA) of density functional theory (DFT).On the basis of the optimization of FeAl supercell ,the formation enthalpy of the Fe or Al atom replaced by Mn atom were calculated respectively,and determined the latter was likely to occur.Then the calculation of elastic constants was carried out, the elastic constants(C11= 305.06 GPa,C12= 145.76 GPa and C44= 132.32 GPa) of FeAl-Mn were got and made a judgment of the stability of FeAl-Mn system.The bulk modulus B(198.86 GPa),shear modulus G(107.95 GPa),young's modulus E(274.22 GPa),possion′s ratio v (0.27) and B/G (1.84) were obtained further by using the Voigt-Reuss-Hill (VRH) approximation.Finally,the enhancement mechanism of Mn doping on FeAl were analyzed in detail through the band structure,density of states,population analysis and differential charge density.It is concluded that the solid solution of Mn increases the charge transfer between atoms, participated in the hybrid, enhanced the combining ability,improve the stability of FeAl etc.
Key words:first-principles; FeAl intermetallics; displacement solution; elastic constants; electronic structure
*收稿日期:2016-04-12
基金项目:国家自然科学基金项目(51171096)
作者简介:王芬(1959-),女,陕西富平人,教授,博士生导师,研究方向:陶瓷/金属复合材料、陶瓷色釉料及古陶瓷科学
文章编号:1000-5811(2016)04-0041-06
中图分类号:TG146.2
文献标志码:A

