拱桥缆索吊装施工索力简化计算方法
罗 亭
(湖南省交通科学研究院 公路勘察设计分院, 湖南 长沙 410015)
拱桥缆索吊装施工索力简化计算方法
罗亭
(湖南省交通科学研究院 公路勘察设计分院, 湖南 长沙410015)
[摘要]缆索吊装施工方法广泛应用于拱桥建设中,为分析吊装过程中缆索索力大小,提出一种以静荷载乘冲击系数来替代滑移移动荷载,将缆索吊装动态过程简化为静态集中力作用下悬链线方程求解的方法。以磨刀溪特大桥施工为背景,应用该方法计算吊装系统的缆索施工阶段的索力,同时对比试吊装试验的实测数据值。研究表明:在吊装过程中,每个施工阶段缆索强度安全系数大于4,满足施工安全。本文提出的简化计算方法适用于缆索吊装施工的缆索索力计算。为拱桥缆索吊装索力计算提供参考。
[关键词]桥梁工程; 缆索吊装; 索力; 悬链线方程
在我国拱桥建设中,缆索吊装施工方法应用较为广泛[1,2]。缆索的安装长度即无应力索长需要精确给出,同时为了保证缆索索力在施工过程中具有足够的安全储备,需精确计算缆索索力需要得到来确定缆索截面设计面积。解决拱桥缆索吊装施工过程中索力大小和线性问题属于分段悬链线计算理论问题[3,4]。缆索吊装系统边跨受力分析与悬索桥边跨拉索受力相同。而主跨受力分析中,吊装系统中为两滑动竖向向下的拉力。相对于悬索桥静力分析更为复杂。建立一种更为简便和准确的计算方法显的尤为重要。本文提出一种以静荷载乘冲击系数来替代滑移移动荷载,将缆索吊装动态过程简化为静态集中力作用下悬链线方程求解方法。
1缆索索力简化计算方法
1.1主跨索力分析(见图1)
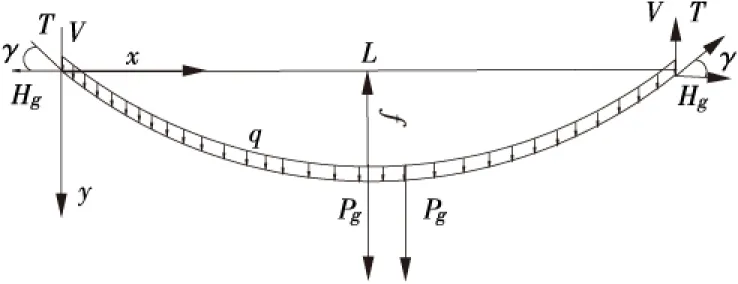
图1 主跨主缆受力示意图Figure 1 The cable stress diagram of mid-span
在缆索系统没有工作时段,主跨缆索只受本身自重作用,缆索的张力为:
(1)
式中:q为缆索单位自重,f为设计垂度,缆索的伸长量为[5]:
(2)
式中:n为矢跨比,E为缆索的弹性模型,A为缆索的面积,L为主跨跨径。缆索自重作用下的有应力索长为[6]:
(3)
自重作用下的无应力索长为:
S0=S-ΔS
(4)
主跨主缆重量为:
G=qS0
(5)
缆索在工作状态下,相当于两个移动向下的拉力,在缆索上进行滑动。线型在不停变化很难求解某时刻工作状态的精确解。将动荷载简化成静荷载作用:
pg=ηpd
(6)
式中:Pd为动荷载,Pg为静荷载,η为动力系数。则索的水平分力为[7]:
(7)
式中:x为集中力作用点距坐标原点的距离。
缆索拉力为索的水平分力与竖向分力的合力,可表示为:
(8)
式中:V为缆索的竖向分力,γ为塔顶缆索的水平夹角。
1.2边跨索力分析
边跨锚啶处拉索的水平分力等于塔顶的水平分力,锚地处竖向分力与边跨缆索的无应力自重之和等于塔顶处缆索的竖向拉力。故边跨的索力分析(见图2),主要是求解边跨索的无应力长度。
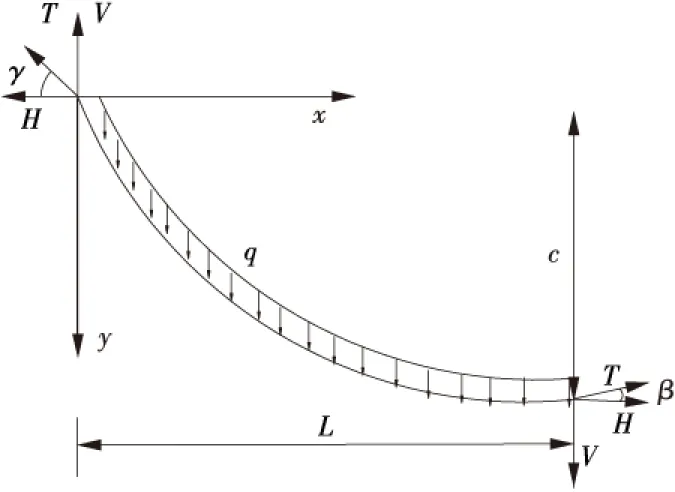
图2 边跨主缆受力示意图Figure 2 The cable stress diagram of side span
可建立图2所示的局部坐标系,索曲线为悬链线满足边界条件的索曲线方程组[8]:
(9a)
(9b)
(9c)
式中:l为边跨跨径,α和β为形状参数。边跨有应力索长表达式[9]:
(10)
边跨无应力索长:
(11)
2工程实例
2.1工程简介
叙古高速公路磨刀溪特大桥主桥为钢筋混凝土劲性骨架上承式拱桥,跨径L=280 m,净失跨比f/L=3.7∶1,拱轴系数m=2.2,为等高截面悬链线无铰拱,采用先分段缆索吊装劲性骨架并合龙,再浇筑混凝土,施工拱上立柱,最后缆索吊装桥面系28 m小箱梁的施工方案。吊装系统主体由扣吊塔(扣塔和吊塔合用)、主缆索、工作索、抗风索和扣锚索组成。其中工作索不参与结构吊装的受力,受水平牵引力作用,主缆为2×3Φ56 mm2的钢绞线,单位重量为q=1.18 kN/m,两边跨主缆与塔顶的水平夹角分别为14°40’和10°4’。主缆吊装立面示意图如图3所示。
2.2荷载工况
缆索吊装施工属于预制拼装工艺,预制构件存放在叙永岸。在施工过程中,部分拼装构件需要从位置A(距离相邻塔5 m)滑移到位置C(距离相邻塔5 m)。在正式施工前,须进行试吊试验确保施工的安全与顺畅。所有吊装构件的重量和长度如表1所示。选用小箱梁作为最不利重量的构件进行试吊试验。分别3个工况。工况A为A点匀速上升起吊小箱梁,工况B为从A点滑移B位置保持静止,工况C为从B点滑移至C点保持静止。
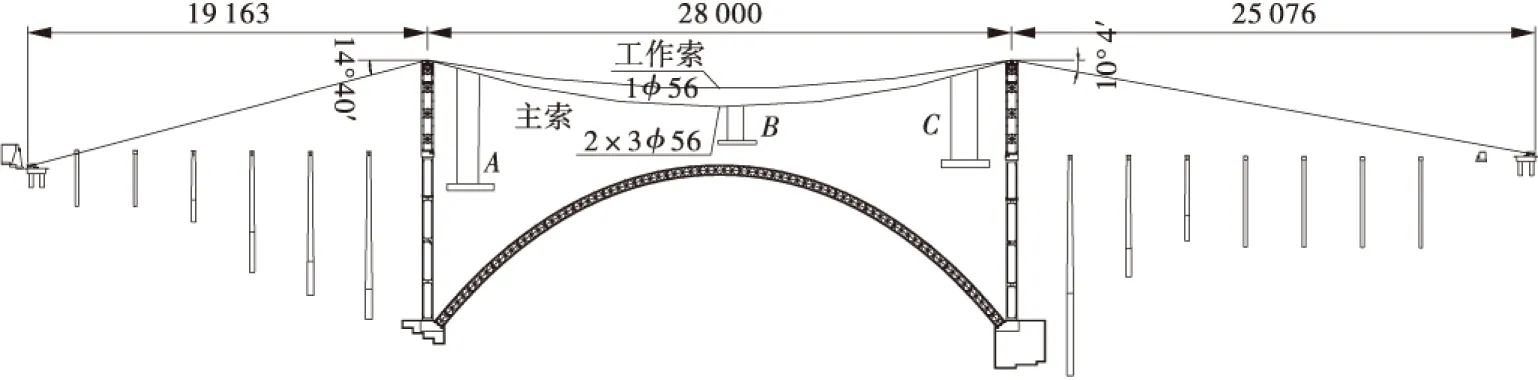
图3 吊装系统示意图Figure 3 The system of cable erection diagram
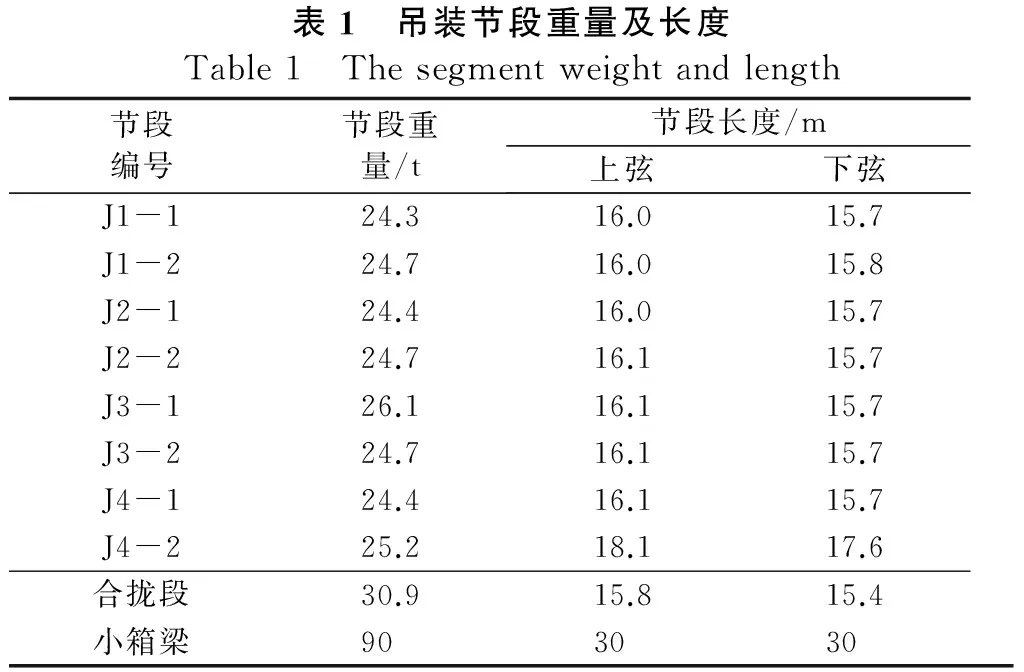
表1 吊装节段重量及长度Table1 Thesegmentweightandlength节段编号节段重量/t节段长度/m上弦下弦J1-124.316.015.7J1-224.716.015.8J2-124.416.015.7J2-224.716.115.7J3-126.116.115.7J3-224.716.115.7J4-124.416.115.7J4-225.218.117.6合拢段30.915.815.4小箱梁903030
主跨荷载分为集中荷载和均布荷载2种。其中集中荷载由吊装节段重Pl、吊具重P2、起吊索重、牵辅助卷扬机重P3、配重P4组成,考虑冲击系数:1.1,其中吊装节段重P1=450 kN,吊具P2=250 kN,P3=50 kN,P4=50 kN;考虑1.1的冲击系数。q为主缆自重均布荷载取值1.18 kN/m。初始设计矢高f=22.4 m。
2.3计算值与实测数据对比
依据本文提出的简化计算方法与缆索系统参数,计算3个工况叙永岸塔顶的拉力与锚啶位置主缆的索为验证本文提出的简化计算方法,在试吊试验过程中,在叙永岸塔顶和锚啶位置分别安置了振弦传感器,对3个施工工况进行应力监测。振弦感器布置如图4所示。采用本文计算方法对3个工况进行索力计算并与实测值进行对比。如表2所示 。

(a) 振弦式应变传感器

(b) 现场吊装示意图
图4试验现场索力测量
Figure 4The measurement of cable force in testing site
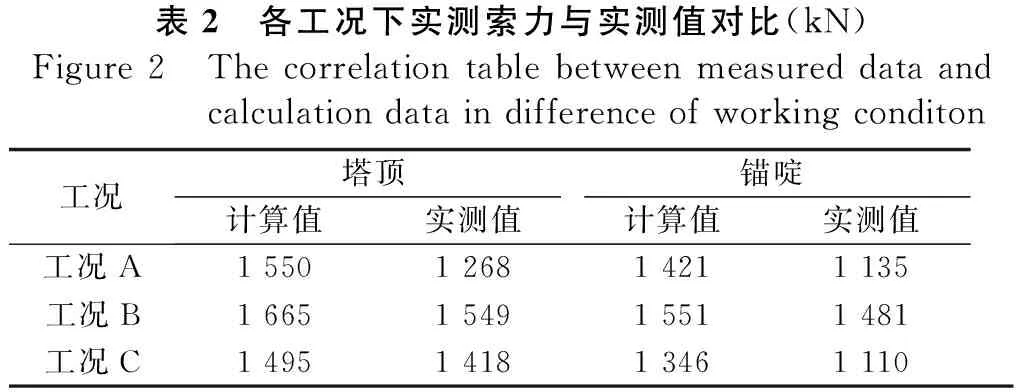
表2 各工况下实测索力与实测值对比(kN)Figure2 Thecorrelationtablebetweenmeasureddataandcalculationdataindifferenceofworkingconditon工况塔顶锚啶计算值实测值计算值实测值工况A1550126814211135工况B1665154915511481工况C1495141813461110
由表2可知,工况A,塔顶和锚啶位置计算值与实测值误差分别为22.1%和25.2%。,工况B两点误差分别为7.4%和4.7%,工况C两点误差分别为5.2%和21.2%。理论计算值普遍大于实测值,计算偏保守。表明该简化计算方法可行。
2.4不同吊装阶段索力
对比实测数据,证明计算方法的适用性。为了分析拱桥施工全过程的安全性,对每个吊装阶段进行索力计算,各阶段索力计算值如表3所示。并验算安全系数K=[T]/T,其中[T]为钢绞线的容许拉力,本文取工程钢绞线的设计容许拉力为7842 kN。依据安全系数公式和表示可知各个施工阶段缆索强度的安全系数值的分布规律。如图5所示。由图5可知: 工况A塔顶缆索和锚啶区缆索的强度安全系数要小于工况B和工况C。在吊装阶段j1-1至J1-9缆索的安全系数维持在一个较高且稳定的状态。到合拢段吊装和小箱梁吊装阶段缆索的安全系数下降较快。应予以监测。
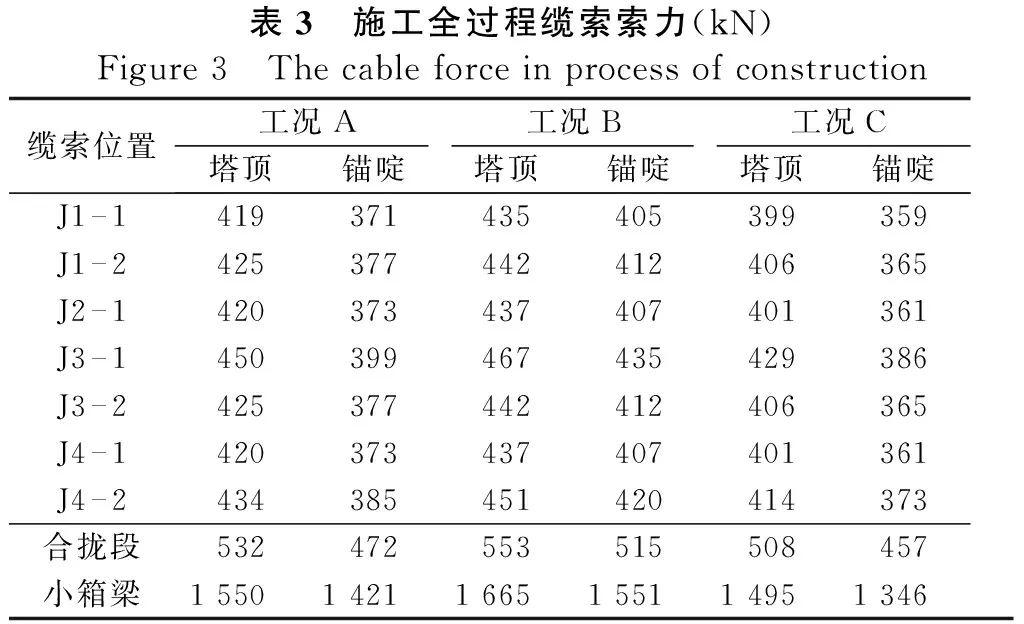
表3 施工全过程缆索索力(kN)Figure3 Thecableforceinprocessofconstruction缆索位置工况A工况B工况C塔顶锚啶塔顶锚啶塔顶锚啶J1—1419371435405399359J1—2425377442412406365J2—1420373437407401361J3—1450399467435429386J3—2425377442412406365J4—1420373437407401361J4—2434385451420414373合拢段532472553515508457小箱梁155014211665155114951346
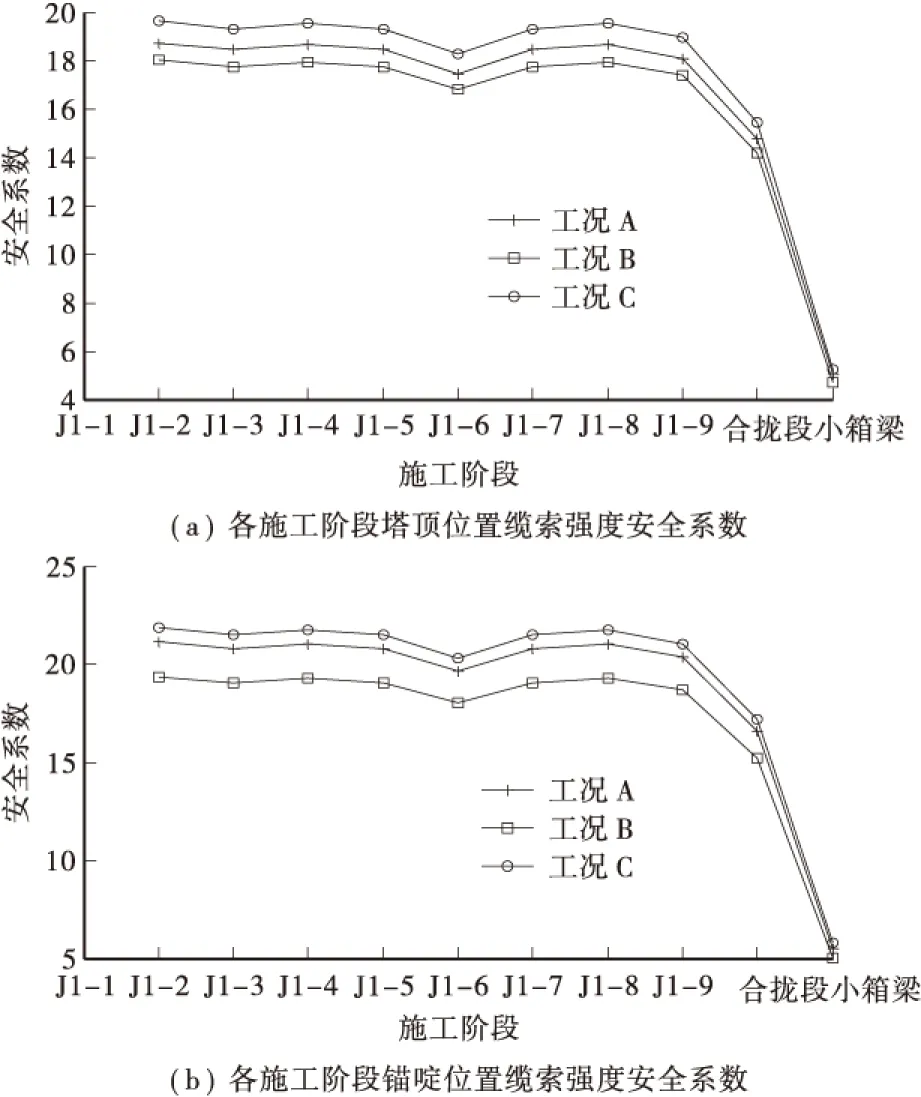
图5 不同施工阶段索力的安全系数Figure 5 The calble safety factor in process of construction
3结论
① 本文提出一种缆索吊装施工中主缆索力的简化计算方法。该方法计算简便且计算量小。便于应用于拱桥缆索吊装索力分析中。
② 在缆索吊装过程中,当阶段滑移至主跨跨中位置时,缆索的强度安全性系数降至最低。应对该阶段进行密切监测。
[参考文献]
[1] 何雄君, 陈巧生. 钢管混凝土拱桥主拱钢管缆索吊装扣索索力调整(英文)[J]. 武汉交通科技大学学报, 1999(05):575-578.
[2]牛润明,安蕊梅.大跨度钢管混凝土拱桥拱肋分段缆索吊装模拟结构分析[J].铁道标准设计,2004(10):12-14.
[3]滕小竹, 贾丽君, 石坚. 大跨度悬索桥空间力学性能研究[J].上海高速, 2010(2).
[4]熊鹰. 猛洞河大桥缆索吊装方案设计和施工[J].公路工程, 2013, 38(5):204-206.
[5]李传习. 混合梁悬索桥非线性精细计算理论及其应用[D].长沙:湖南大学, 2006.
[6]朱建甫. 自锚式悬索桥吊索安装施工控制研究[D].成都:西南交通大学, 2008.
[7]檀永刚. 自锚式悬索桥的力学特性与施工控制研究[D].大连:大连理工大学, 2008.
[8]肖海波.自锚式悬索桥的力学特性分析[D].杭州:浙江大学, 2004.
[9]彭文立. 钢管拱肋缆索吊装施工控制及模糊推理系统的应用[D].南宁:广西大学, 2005.
The Method of Cable Force Calculation in Process of Cable Erection Construction for Arch Bridge
LUO Ting
(Hunan Communications Research Institutehighway Survey and Design Branch Court, Changsha, Hunan 410015, China)
[Abstract]The cable erection construction are wide using in process of arch bridge construction, in order to analysis the cable force , we proposed a simple method which used the dead load multiplication by impact coefficient instead of dynamic load to calculate the cable force, then the dynamic solving process were changed into the problem of catenary equation under the action of single force. On the basis of project of Mo Dao Xi grand bridge,the method of cable force calculate were used in the project of cable erection. The value of cable force between calculated and measured was fitted. The research show that the cable safety factor are higher than 4 in process of bridge construction. The calculation method that we proposed are apply to the arch bridge construction.
[Key words]bridge engineering; cable erection; cable force,catenary equation
[收稿日期]2015-12-21
[作者简介]罗亭(1983-),男 ,湖南湘西人,硕士,从事公路桥梁设计科研工作。
[中图分类号]U 445.46
[文献标识码]A
[文章编号]1674-0610(2016)03-0122-03

