基于函数梯度无网格自适应方法研究
杨贺奎,丁 宁,徐江荣
(杭州电子科技大学能源研究所,浙江 杭州 310018)
基于函数梯度无网格自适应方法研究
杨贺奎,丁宁,徐江荣
(杭州电子科技大学能源研究所,浙江 杭州 310018)
摘要:以计算一维泊松方程为例,通过研究节点分布对无网格法数值模拟的影响,提出了一种基于函数梯度大小调整节点密度的自适应方法.首先利用无网格法求出函数的近似梯度函数,然后分析该函数的梯度值,在梯度较大的位置加密计算节点,以提高计算精度,减少数值模拟的误差.利用该方法计算二维圆柱绕流N-S方程,模拟计算的结果基本符合圆柱绕流现象,表明了基于函数梯度进行节点加密的方法达到了很好的效果.
关键词:梯度函数;无网格方法;节点分布;RPIM形函数
0引言
在解决工程数值分析领域中,传统网格法的运用出现了许多难于求解的问题.特别是对于气固两相流运动界面不连续的问题,模拟时往往产生不能求解网格极端扭曲或难于跟踪自由表面等难题.网格法在求解计算时,需要不断地重新划分网格,使得计算量增大,计算精度降低,稳定性变差.为了解决这一难题,文献[1]提出利用无网格法来解决相关问题.无网格法在数值计算中不需要将节点连接成网格单元进行划分和重构,而是按照一些任意分布的坐标点构造插值函数离散控制方程,能方便地模拟各种复杂形状的流场[2].因此无网格法为计算流体力学的自适应分析、界面追踪、多相流动等方面开辟了一个极具诱惑的新途径.然而运用无网格法计算有一个很大的问题,其计算量几乎和计算节点数成正比,随着节点数的增加,计算量迅速增大[3].如何保证在计算总节点数一定的情况下,提高计算精度成为一个难题.本文以计算一维泊松方程为例,通过研究节点分布对无网格法流场数值模拟的影响,提出了一种基于函数梯度大小调整节点密度的自适应方法.
1基于函数梯度大小进行节点加密分析
无网格法可以任意地在计算区域内布点,不同的布点方式给模拟计算精度带来不同的影响.一般情况下,函数梯度反映了函数变化的趋势,在高梯度的位置函数的变化比较大,因此在这些位置应该多分布一些节点,如果分布的节点比较少必然会增大数值模拟的误差[4].
1.1一维泊松方程
下面以计算一维泊松方程为例,使用配点法模拟,研究如何进行节点加密,使得在计算总节点数一定的情况下,得到较高的模拟计算精度.其解析函数梯度绝对值分布如图1所示.
由图1可以看出,前半部分比后半部分的梯度小,这说明该函数值在前半部分变化要比后半部分变化小.因此为了减少计算误差,在函数梯度较大的位置进行节点加密.为了验证这一想法,本文先对前半部分节点加密,再对后半部分节点加密,比较这两种情况下数值模拟的平均误差.加密的方案是在原来均匀分布的平均间距上等间距地增加一些节点.
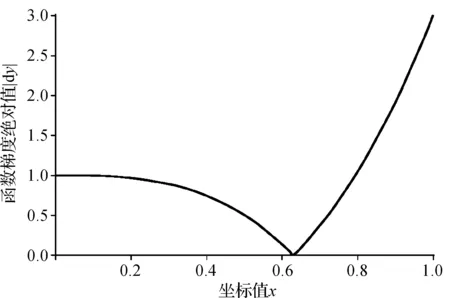
图1 解析函数梯度绝对值分布图
1)前半部分的节点加密
前半部分节点加密后,平均误差随节点个数变化如图2所示.
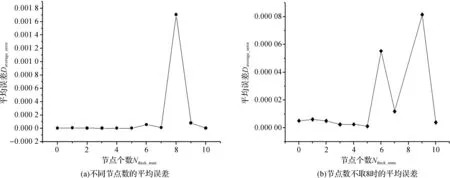
图2 前半部分节点加密引起的平均误差随节点个数变化图
从图2(a)中可以看到,在前半部分平均间距中,计算节点数增加到8时,平均误差迅速猛增.
为了进一步体现加密效果,图2(b)去掉了图2(a)中Nthick_num=8时Daverage_error的数值.可见,在平均间距中增加1~2个节点,其平均误差并没有下降,增加1个节点还导致平均误差变大.但继续增加节点,平均误差就减小了.当Nthick_num>6时,Daverage_error比Nthick_num=0时增大了很多,说明加密过度使得平均误差变大,并不能使计算精度有所提升.因此,要进行局部节点的加密,就需要经过一个度量的过程,过度加密是没有意义的.
2)后半部分的节点加密
后半部分节点加密后,高梯度处平均误差随节点个数变化如图3所示.
从图3(a)中可以看出,在后半部分平均间距中,计算节点数增加到5时,平均误差迅速猛增.
为了进一步体现加密效果,图3(b)去掉了图3(a)中Nthick_num=5时Daverage_error的数值.当Nthick_num>6时,Daverage_error的数值比Nthick_num=0时大,这也说明了加密过度使得平均误差变大.就本算例而言,在平均间距中增加1~2个节点就使得精度有所提升.由图3(b)可以看出,在平均间距中增加1~2个节点效果是最好的,总体效果也比前半部分加密好.这说明在梯度比较大的位置加密比在梯度小的位置加密效果更好,精度更高.
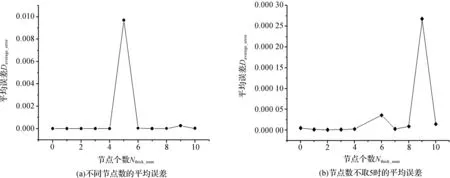
图3 后半部分节点加密引起的高梯度处平均误差随节点个数变化图
1.2根据近似函数计算函数梯度方法
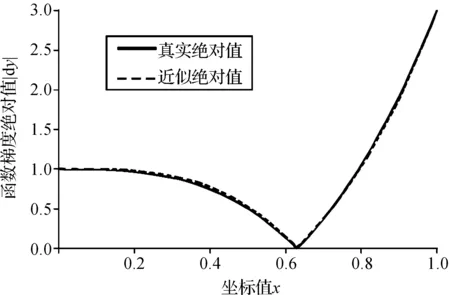
图4 近似函数梯度绝对值分布图
一般情况下,进行数值模拟时,不知道所求函数的解析解,也就不知道该函数的梯度函数,故而无法确定函数值变化的大小.本文提出使用近似函数的方法,即先在均匀分布的节点上算出数值解,再利用形函数的导数,近似求出函数梯度值.
下面验证根据近似函数计算函数梯度的方法是可行的.近似函数梯度绝对值分布如图5所示.
由图4可以看出,利用近似函数求解的梯度函数的数值解和解析解基本上重合的,因此可以认为这种方法是可行的.
1.3不同位置加密方法的函数误差
在泊松方程下不同加密方法的函数误差分布如图5所示.
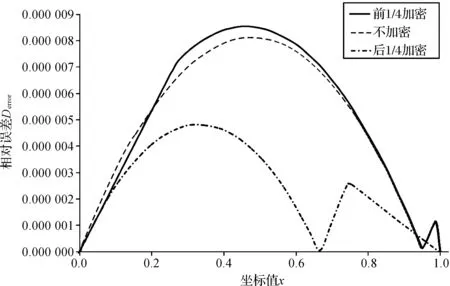
图5 泊松方程不同加密方法下函数误差分布图
图5中,Derror=|u(xi)real-u(xi)h|,即表示每1个节点的相对误差.由图5可以看出,后1/4加密函数误差相对较小,前1/4加密函数误差相对较大,所以在函数梯度大的位置加密效果比较好,在函数梯度小的位置加密效果不太好.
2基于不同节点加密影响域PDE的模拟计算
为了进一步验证基于函数梯度进行节点加密的方法的可行性,采用无网格径向基插值法(RPIM)对二维圆柱绕流N-S方程进行模拟验证.在该工况中,圆柱周围流场的速度变化是最大的,函数梯度也是相对较大的,因此要在圆柱周围进行节点加密.
2.1圆柱绕流N-S方程
2.1.1数学模型
圆柱绕流的主控制方程采用原始变量形式的二维非定常不可压缩流N-S方程,在惯性参考系下其无量纲形式为.
2.1.2计算区域和边界条件
设定计算区域,水平方向为x方向,竖直方向为y方向.水平长度为1 m,竖直长度为0.5 m.圆柱圆心坐标为(0.2,0.2),进口速度U=0.01 m/s.流动方向与垂直流动方向上的均匀速度分别定义为u和v.
进口处:给定进口速度,u=U,v=0;
出口处:在计算区域出口处,设置自由出口条件.假定在任意时刻下计算区域出口处的流动都已充分发展,那么各速度分量和压力均取第二类边界条件,即
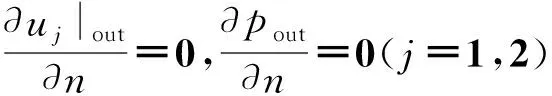
上下边界:为消除固壁带来的尺寸效应,给定u=U,v=0;
圆柱表面:给定无滑移,无穿透边界条件,u=0,v=0;
二维非定常不可压缩流N-S方程是非线性方程,含有抛物型和椭圆型两种性质.一般的解法是不行的,本文采用数值方法—速度修正法即分裂步数法进行迭代求解,时间离散采用差分方法,空间离散采用无网格径向基插值法(RPIM)[5].在整个流场中,只有在圆柱周围的梯度变化是最大的,因此在圆柱周围进行节点加密,形成一个云状结构,节点分布如图6如示.
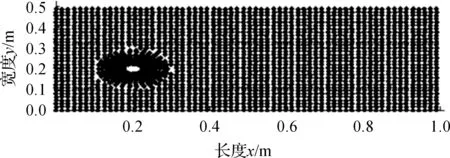
图6 圆柱绕流节点分布图
无网格径向基插值法(RPIM)属于全局弱式的积分方法.使用该方法需要1个背景网格,并在每个网格单元内均匀地分布高斯点.影响该方法计算精度的因素主要是影响域半径、时间步长、影响域内保留的节点个数.这3项数值的大小不仅影响到数值计算的精度,而且很大程度上影响了计算的时间.因此要求影响域半径尽量小,影响域内保留的节点个数保持在20以内.为提高数值计算的精度,时间步长采用变步长的形式进行求解.时间步长序列为
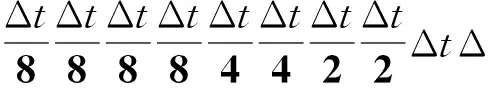
下面对控制方程进行离散:
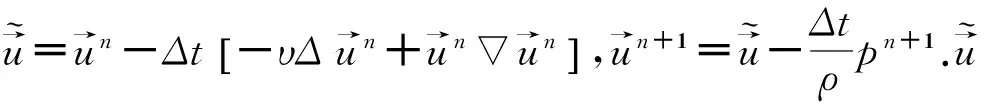
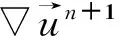
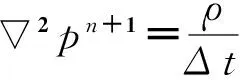
通过以上分析,求解圆柱绕流N-S方程,根据自适应分析理论,在圆柱周围进行节点加密,形成一个节点密度较高的云状结构,而在其他位置节点分布比较稀疏.
2.2模拟计算结果分析
利用Tecplot软件引入数值求解圆柱绕流N-S方程,在圆柱周围进行节点加密,当圆柱绕流速度场变化到某个时刻时,圆柱绕流速度矢量发生的变化情况如图7所示.
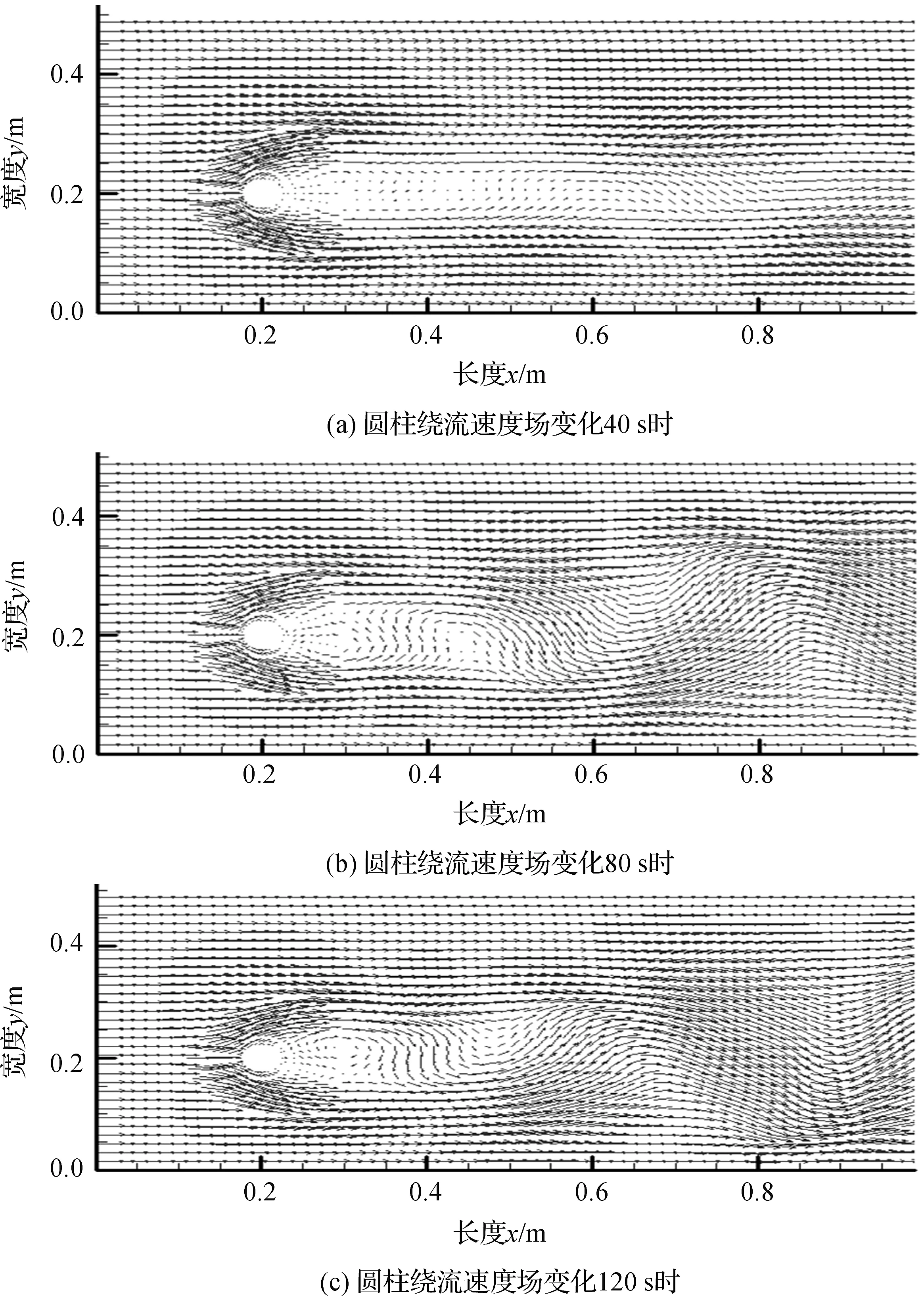
图7 圆柱绕流速度矢量变化情况
图7中,当圆柱绕流速度场变化40 s时圆柱后方开始形成漩涡;80 s时已经形成了漩涡,而且在圆柱的后方还可以看到脱落的漩涡.120 s时流场已经基本充分发展,在圆柱的后方已有明显的小漩涡,脱落的漩涡也很明显.这个结果基本符合圆柱绕流的现象,表明了基于函数梯度进行节点加密的方法是可行的.
3结束语
本文研究了基于函数梯度大小调整节点密度的自适应方法,利用无网格方法先求出近似梯度函数,再根据梯度函数来确定节点加密的位置.得出在高梯度的位置进行节点加密,可以减少数值模拟误差,提高计算精度,但注意不要过度加密,否则会适得其反.并通过计算二维圆柱绕流N-S方程进行模拟验证,模拟结果基本符合圆柱绕流的现象,验证了本文方法的有效性.
参考文献
[1]李九红,程玉民.无网格方法的研究进展与展望[J].力学季刊,2006,27(1):143-152.
[2]LIU Y, ZHANG X, LU M W. Meshless Least-Squares Method for Solving the Steady-State Heat Conduction Equation[J]. Tsinghua Science and Technology, 2005,10(1):61-66.
[3]仇轶,由长福,祁海鹰,等.无网格方法中的结点分布算法[J].数值计算与计算机应用,2006,27(3):176-182.
[4]张雄,刘岩,马上.无网格法的理论及应用[J].力学进展,2009,39(1):1-36.
[5]夏茂辉,贾延,刘才.基于径向基函数的点插值(RPIM)无网格法[J].燕山大学学报,2006,32(2):112-117.
The Research of the Adaptive Method about Adjusting the Node Density Based on the Meshless Method
YANG Hekui, DING Ning, XU Jiangrong
(InstituteofEnergy,HangzhouDianziUniversity,HangzhouZhejiang310018,China)
Abstract:This paper is based on calculating the Poisson equation as an example, through the study of node distribution effect on numerical simulation in the flow field by using the meshless method, presents an adaptive method about adjusting the node density based on the function gradient size. It is using meshless method to calculate the approximate gradient functions, and analyze the gradient value of the function. Using the multi-distribution of some nodes in the location of function gradient higher, to improve the calculation accuracy and reduce the error of the numerical simulation. By using this method to calculate the N-S equation of the flow around a circular cylinder, the simulation results are basically in accord with the flow around the cylinder. It is indicated that the method of node encryption based on functional gradient has achieved good results.
Key words:the gradient function; the meshless method; the node distribution; the RPIM shape function
DOI:10.13954/j.cnki.hdu.2016.04.018
收稿日期:2015-10-19
基金项目:国家自然科学基金资助项目(51176044);浙江省自然科学基金资助项目(Y1111085)
作者简介:杨贺奎(1992-),男,安徽亳州人,硕士研究生,能源机械.通讯作者:丁宁副教授,E-mail:tinin@hdu.edu.cn.
中图分类号:O241
文献标识码:A
文章编号:1001-9146(2016)04-0084-06

