小波能量熵与BP神经网络算法在数传设备故障诊断的应用研究*
刘天庆,赵玉刚
(1.中国电子科技集团公司第二十研究所,陕西 西安 710068;
小波能量熵与BP神经网络算法在数传设备故障诊断的应用研究*
刘天庆1,赵玉刚2
(1.中国电子科技集团公司第二十研究所,陕西 西安 710068;
2.火箭军工程大学士官职业技术教育学院,山东 青州 265001)
摘要:根据检测设备采集的数传设备故障样本信号,采用小波分析方法,提取信号的小波能量熵,并将其与其他特征参数一起形成特征向量,利用训练好的BP神经网络模型对设备故障进行诊断,从而确定设备故障模块。结果表明,该方法在数传设备故障诊断中具有较高的故障诊断率。
关键词:小波能量熵;BP神经网络;故障诊断
针对复杂的数传设备,采用传统的BP神经网络进行故障诊断,存在着输入维数多、结构规模大、训练时间长等问题。本文将小波分析方法运用于数传设备故障诊断中,通过提取信号的小波能量熵,结合其他特征参数,对采集的样本信号进行了预处理,剔除了信号中的冗余量,所以能减小神经网络规模,加快神经网络的训练速度,从而准确高效地完成了设备的故障诊断。
1基于小波能量熵的故障特征提取方法
1.1小波变换的基本理论[3-5]
离散小波变换(Discrete Wavelet Transform,DWT)是指尺度伸缩参数a和时间平移参数b进行离散化,而不是时间的离散化。

(1)
则离散小波序列为:

(2)
对f(t)进行离散小波变换,其离散小波变换系数为:

(3)
其相应的离散小波变换的重构(即逆变换)公式为:
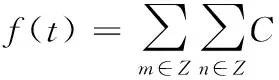
(4)
特别地,取a0=2,b0=1,对尺度伸缩参数a和时间平移参数b进行二进离散,即:
a=2m,b=n2m.
(5)
可得二进小波(Dyadic Wavelet)序列和二进小波变换系数分别为:

和
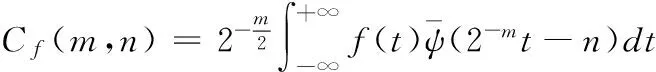
(6)
可以证明{ψm,n}m,n∈z构成空间L2(R)的一组标准正交基,即

(7)
由以上分析可知,二进小波变换的实质是将属于L2(R)的任一函数f(t)用离散小波序列的形式进行展开,而小波序列则是在小波基函数的基础上伸缩得到的。随着伸缩因子(尺度因子)m的变化,得到函数在不同尺度空间的投影,伸缩因子越小则分辨率越高。
1.2基于小波能量熵的故障特征提取方法
首先给系统以某一激励信号,在不同的故障模式下,对采样点输出信号以一定时长进行采样。将采样获得的信号进行小波分解,获得相对能量并计算出小波能量熵。具体步骤[1]如下:
1) 在不同的故障模式下,给系统以某一确定信号,对采样点进行信号采样,将测得的连续信号离散化;
2) 将离散化的数据加载到MATLAB程序中,利用一维小波分解函数将输入的离散化波形数据进行小波分解,得到小波近似系数cAi和细节系数cDi;
3) 利用小波能量获取函数,获得波形数据对应的近似系数和细节系数的相对能量;
4) 利用小波能量熵计算函数,在选择相应能量熵类型后,获取对应的小波能量熵。
2BP神经网络结构与算法
BP神经网络的结构一般包括输入层、输出层和隐含层。隐含层可以是一层,也可以是多层。万能逼近定理证明[6-9]:含一个隐含层的三层BP神经网络,只要隐含层节点数足够多,该网络就能以任意精度逼近有界区域上的任意连续函数。
BP神经网络结构具有以下特点:1) 是多层感知器神经网络,即网络由多层构成;2) 各层之间只能向前连接,层内之间不能有连接;3) 误差由后向前依次传播,这也是误差反向后传的由来;4) 激活函数必须处处可导,在BP网络中一般采用S型激活函数。
BP神经网络的学习过程包括信号的正向传播、误差的反向传播两个阶段。
正向传播阶段:信息从输入层输入,经过隐含层处理后由输出层输出。反向传播阶段:如果输出层得不到期望输出,那么期望输出与真实输出之间就会存在误差,用此误差来估计输出层的直接前导层的误差,再用这个误差估计更前一层的误差。如此一层一层的反传下去,就获得了所有其他各层的误差估计,以此对各层单元的权值进行修正。如此循环往复,直到网络最终输出的误差减少到可以接受的程度或进行到预先设定的学习次数为止。
3基于小波能量熵和BP神经网络的故障诊断过程
将获得的小波能量熵与其他特征参数一起,形成故障诊断的特征向量,对BP神经网络进行训练。然后,将测试数据输入到已训练好的BP神经网络中进行模式识别,从而完成对系统的故障诊断。数传设备故障诊断过程如图1所示。
1) 根据设备的故障模型,确定各模块在不同的故障模式下的关键特征信号及信号采样点。
2) 将某特定波形的连续激励信号送入设备,并在满足采样定理的条件下,以一定时长对各采样点的信号进行采样。
3) 利用1.2中小波故障特征提取方法,获得各采样信号的小波能量熵,与其他特征参数一起形成故障诊断的特征向量,并进行归一化,以此作为BP神经网络的训练样本和测试样本。
4) 完成对BP神经网络的训练。将预处理后的测试信号送入训练好的BP神经网络,根据输出结果判断设备故障模块。

图1 数传设备故障诊断过程
4故障诊断仿真实现
本文以某型数传设备“抗干扰收正常,发不正常”的故障状态为例进行分析。根据对该数传的工作原理、故障树模型分析及专家经验,在此故障状态下可能故障模块与特征参数的对应关系如表1所示。

表1 数传“抗干扰收正常、发不正常”故障对应关系
第一步,建立故障诊断模型
建立三层神经网络。输入层:从设备对象中测得的故障特征参数值;隐含层:将输入层输入的故障参数值进行处理;输出层:针对不同的故障参数值,经过隐含层处理后,得到的故障模式。本例中,输入层神经元为6个,分别对应UUT发信端电流(I)、侧音电平(V)、侧音响应(Y)、频率误差(E)、发射功率(P)、侧音失真(T)。输出层神经元为4个,分别对应4种不同的故障模式:前面板模块故障(F-1)、同步模块故障(F-2)、激励模块故障(F-3)、功放模块故障(F-4)。根据Kolmogorov定理[2],如果输入层神经元个数为n,则隐含层的神经元个数可以取为2n+1。这里取隐含层神经元的个数为13个。
第二步,提取故障特征
由于其中电流和电压数据为波形数据,如果采用有效值,会丢失很多特征信息,所以此处采用小波分析的方式,将电流和电压波形数据转化为小波能量熵,结合其他特征参数值共同形成特征向量。将设备分别置于4种不同的故障模式及正常状态下,利用以上方法采集100组样本数据,对建立的BP神经网络进行训练。表2为BP神经网络目标输出,表3为部分故障样本数据进行归一化后的数据。
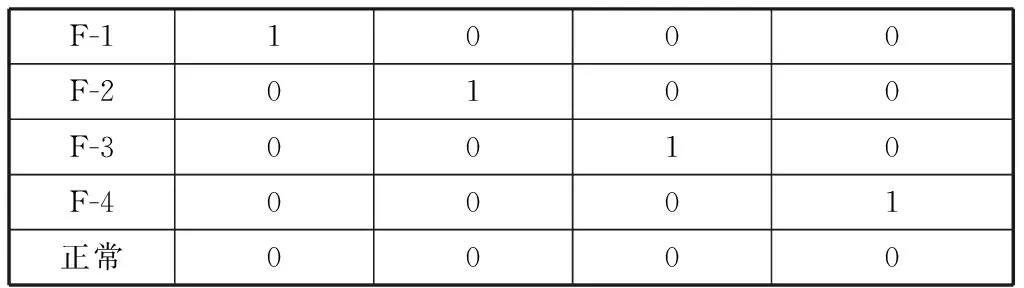
表2 神经网络目标输出模式

表3 第60组归一化后的故障样本数据
第三步,BP神经网络训练
1) 网络参数设置
net=newff(minmax(x),[13,4],{’tansig’ ’logsig’}):隐含层有13个神经元,输出层有4个神经元,网络激活函数采用S型函数,隐含层激活函数为tansig,输出层激活函数为对数函数logsig。
net.trainParam.mc=0.9:网络中动量因子设为0.9。
net.trainParam.epochs=10000:最大训练次数设为10000。
net.trainParam.goal=0.001:网络误差精度设为0.001。
net.trainParam.lr=0.1:学习速率为0.1
2) 函数选择
在进行BP神经网络训练时,存在训练函数和学习函数如何选择的问题,选择的函数不同,达到误差精度时的迭代次数也不相同,如表4所示。
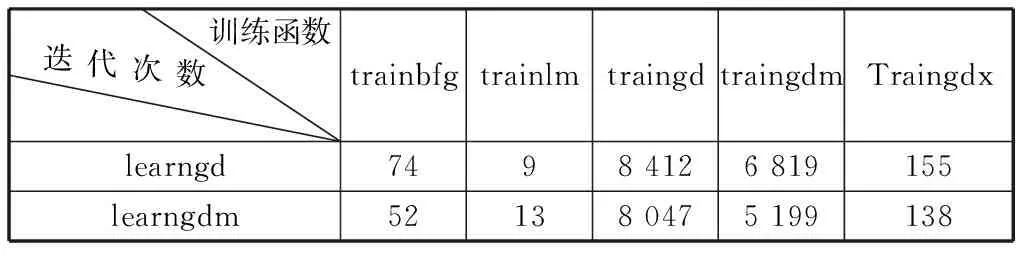
表4 不同学习函数与训练函数的训练迭代次数
由上表可知,训练函数选择learngd,学习函数选择trainlm时,迭代次数最少,训练速度最快,达到0.001的精度只需要9步。训练函数选择trainbfg或traingdx时,也可以较快达到要求精度。当训练函数选择traingd和traingdm时,要达到所需精度,需要训练步数在5 000步以上,效果较差。所以,在进行仿真时,选择训练函数为trainlm,学习函数选择learngd。
对归一化后的采样数据进行BP神经网络进行训练,训练误差曲线如图2所示。
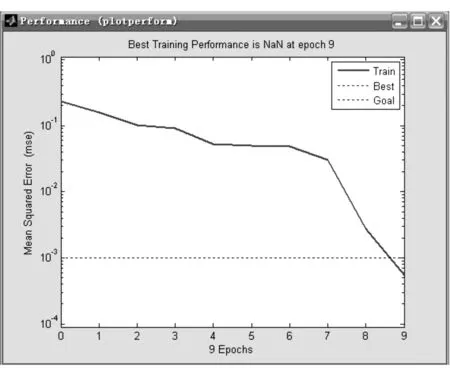
图2 网络训练误差曲线
第四步,利用BP神经网络进行故障诊断
任取4组不同故障模式下的测试数据(如表5所示),作为训练好的BP神经网络的输入。根据BP神经网络输出结果进行故障诊断。表6为神经网络的输出结果。
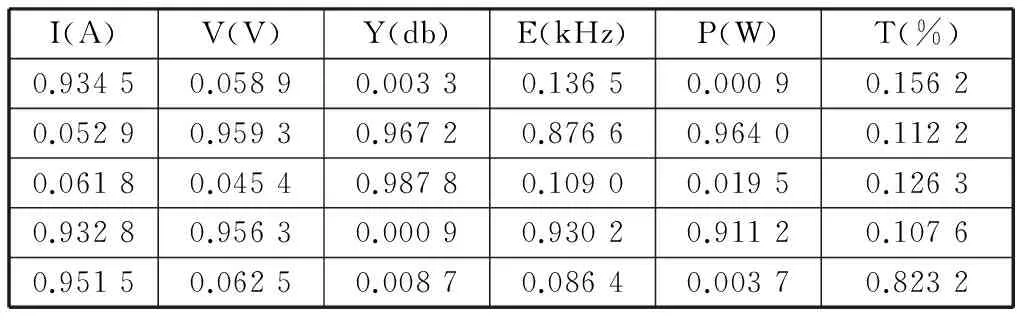
表5 测试数据归一化

表6 神经网络输出结果
根据神经网络输出结果可以发现,输出值近似为1000、0100、0000、0001和0010,分别与BP神经网络设置的不同模式相对应,即F-1模块故障、F-2模块故障、工作正常、F-4模块故障、F-3模块故障,而这也正好与预先设置的故障类型是一致的。
5结束语
本文利用小波的方法对故障样本信号进行预处理,将获得的小波能量熵作为部分故障特征值,并利用BP神经网络完成了数传设备的故障诊断。不仅将其中的故障信息进行了最大程度的保留,而且有利于故障诊断的实现。通过实验数据可知,将小波能量熵作为数传设备故障特征值,并利用BP神经网络进行故障诊断的方法是可行的,诊断结果较为准确。
参考文献
[1]白航,赵拥军,赵国庆,等.一种改进的雷达信号小波包特征提取方法[J].信息工程大学学报,2012,13(1):90-94.
[2]钱敏平,龚光鲁.随机过程论[M].北京:北京大学出版社,2000.
[3]张德丰.MATLAB小波分析[M].北京:机械工业出版社,2009.
[4]侯遵泽,杨文采.小波多尺度分析应用[M].北京:科学出版社,2012.
[5]赵海滨.MATLAB应用大全[M].北京:清华大学出版社,2012.
[6]Cybenko G.Approximation by Superposition of a Sigmoidal Function[J].Mathematics of Control,Signals,Systems,1989,2(4):303-314.
[7]Homik K,Stinchcombe M,White H.Multilayer Feed Forward Networks are Universal Approximators[J].Neural Networks,1989,2(5):359-366.
[8]Cotter N.The Stone-weierstrass Theorem and Its Applications to Neural Networks[J].IEEE Trans.On Neural Networks,1990,1(4):290-295.
[9]Ito Y.Representation of Functions by Superposition of a Step or Sigmoidal Function and Their Application to Neural Network Theory[J].Neural Networks,1991,4(3):385-394.
Application of Wavelet Energy Entropy and BP Neural Network Algorithm in Fault Diagnosis for Digital Transmission Equipment
Liu Tianqing1, Zhao Yugang2
(1.TwentiethResearchInstituteofChinaElectronicTechnologyGroupCompany,XianShaanxi721006,China;2.CollegeofVocationTechnologyEducationofPettyOfficer,RocketArmyUniversityofEngineering,QingzhouShandong265001,China)
Abstract:According to the number of fault sample signal of digital Transmission equipment, using the method of wavelet analysis, the wavelet energy entropy of signal is extracted in the article. The entropy itself and other characteristic parameters are formed together to be a feature vector. The trained BP neural network model is used to diagnose the equipment fault so as to determine the fault module. The results show that this method has a high rate of fault diagnosis in the fault diagnosis for digital transmission equipment.
Key words:wavelet; energy entropy; BP neural network; fault diagnosis
收稿日期:2016-04-24
基金项目:国家自然科学基金资助项目(60874112)
作者简介:刘天庆(1957- ),男,陕西西安人,高工,主要从事智能故障预测与诊断方向的研究。
文章编号:1674- 4578(2016)03- 0090- 03
中图分类号:TP 273.4
文献标识码:A

