集成电路企业工序能力初探
弓 伟,周晋阳
(长治医学院 生物医学工程系,山西 长治 046012)
集成电路企业工序能力初探
弓伟,周晋阳
(长治医学院 生物医学工程系,山西 长治 046012)
摘要:主要讨论了集成电路企业工艺能力指数的定量表征和计算方法,并结合数据分析软件MiniData对具体产品的工艺能力进行了分析说明。
关键词:工艺能力指数;正态分布;标准差
1概要
CPK,即Process Capability index的缩略形式,通常被译为工序能力指数,或是工艺能力指数、制程能力指数等。CPK是指工序在一定的时间里,处于稳定状态下的实际加工能力。
CPK是工序本身所具有的保证产品质量的能力。工序,是指5M1E六个基本质量因素综合作用的过程,亦即产品质量的生产过程。工序中的各个质量因素决定了最终产品的质量,换句话说,产品质量是各质量因素的综合表征。产品质量分散的存在于整个生产过程。产品质量特性值的分散越小,说明工序能力就越高;反之,则说明工序能力越低[1]。
集成电路行业的整体工艺技术水平和要求都比较高,对于我国这样一个集成电路制造大国来说,不断提高集成电路企业的工序能力显得尤为重要。
2工序能力的定量表征
2.1工序能力
工艺参数一般都服从正态分布N(μ,σ2),如图1所示。

图1 正态分布图
图1中,标准差σ的大小反映了参数的分散程度。μ±3σ的范围内,集中了绝大部分的数值,占到99.73%的比例。我们将6σ称之为是工序能力。6σ包含的范围越小,说明工艺参数就越集中,工序能力越强,即生产出高成品率和高可靠性的产品的能力就越强。
2.2潜在工序能力指数CP(Process Capability index)
2.2.1双侧公差情况
在实际工业生产过程中,常使用下式定义工序能力指数:
CP=(USL-LSL)/6σ=T/6σ
其中,USL、LSL分别表示规格上限和规格下限。
积分可以得出成品率为:
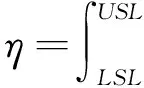
上式中,F(x)为正态分布N(μ,σ2)的函数表达式。
通过积分计算,得到工序能力指数与成品率的关系(PPM表示百万分比)。

表1 工序能力指数与成品率关系
易得:工序能力指数与成品率呈正相关的关系。
2.2.2单侧公差情况
在某些生产过程中,工艺参数只有下限(如反向击穿电压)而无上限,则工序能力指数应当按照以下公式计算:
CPL=(μ-LSL)/3σ.
如果μ 若工艺参数规范只规定上限值(如静态噪声)而无下限要求,则工序能力指数应当按照以下公式计算: CPU=(USL-μ)/3σ. 如果μ>USL,则取CPU为零,即完全没有工序能力。 2.2.3CP的评价指标 通常,工业生产对于工序能力指数的要求见表2。 表2 工业生产对工序能力指数的要求 CP的值越大,工序能力越好。通常,CP位于0到2之间。CP=0.67对应于2σ水平;CP=1对应于3σ水平;CP=1.33对应于4σ水平。当然,对于实际生产过程来说,CP的值也并非越大越好。当CP≥1.67时过于好,这个阶段可以考虑降低成本,简化管理要求。 2.3实际工序能力指数CPK 2.3.1准确度与精密度的综合指数——CPK 闭环的工艺控制在实际生产过程中使用的并不多,大部分情况下都是进行间接的控制,故标准值的中心与工艺参数的中心很难相等。集成电路行业的工艺水平较高,但仍采取间接的工艺控制方法。在集成电路的生产工艺过程中,通常都是先做试件,再根据试件的结果调整工艺。 使用间接的工艺控制方法,标准值的中心与工艺参数的中心一般会有1.5σ的偏移。所以,CPK在某些特定情况下表示为CP,即当公差的中心与工艺参数的中心合二为一时,CPK表示为CP;当公差的中心与工艺参数的中心不相等时,工序能力指数仍然为CPK。 在标准值的中心与工艺参数的中心有1.5σ偏移的情况下,CPK一般比CP小0.5[2]。因此,CP又被称为是潜在工序能力指数,而CPK被称为实际工序能力指数。 图2 标准值的中心与工艺参数的中心偏移1.5σ 标准值的中心与工艺参数的中心不相等时,CPK的计算公式如下所示: 2.3.2CPK的评级标准 表3 CPK的评级等级及措施 3工序能力指数的计算 由工序能力指数的计算公式可知,标准差σ的计算是关键。 3.1短期标准差 短期是一个相对的概念,只考虑自然的随机的一般原因变异。 短期标准差的数据与选择的计算方式有关,从而决定了CPK指数的计算。标准差有三种不同的方式: 1) 极差: 表4 子组个数与固定系数的关系 亦可用经验公式计算:d2=0.122 2+0.598 85n-0.031 92n2(n≥2) 2) 标准差: 子组的标准差按照如下公式计算: 短期标准差为: 表5 子组个数与固定系数的关系 3) 合并标准差: 式中:r为分组数,ni为子组大小 。 3.2长期标准差 长期标准差考虑两种变异因素:一般原因和特殊原因。通常,需要一个包含长期变异的抽样来计算。在工艺过程中如果有操作者、仪器设备、材料等变异的话,需要考虑这些变异。 长期标准差不考虑每个样本子组间的变差,是总体的变差,计算公式如下: 4利用数据分析工具MiniData进行工序能力分析 利用数据分析工具MiniData可以方便、快捷、准确地分析出工序能力,并将分析结果以直观的方式显示。 例如某电子元器件制造企业的某产品数据如表6所示,标称值为15.00,规格上限为15.10,规格下限为14.90。 表6 某产品系列数据 利用MiniData进行工序能力分析,可得如图3所示工序能力分析图。 图3中的PPK表示长期过程能力指数。如果针对的是单量比较少的情况,则应当使用CPK作为评价的标准更为合适。由分析图可知,工序能力为A级,能力良好,状态稳定。 如果工序能力不达标的话,就需要深入查找原因。原因一般可分为两类:偶然因素与异常因素。其中,偶然因素对质量的影响比较小,但却是始终存在的,难以避免;而异常因素虽然对质量影响大,可以采取有关措施消除。所以,异常因素引起的质量的异常波动是我们在实际生产过程中需要重点关注和监控的。发生了质量的异常波动后,应当在尽可能短的时间内查找出问题原因,并实施相关措施解决问题,并且将其纳入到标准中去,确保问题不再出现。 图3 某产品工序能力分析图 5总结 对于工艺水平较高的集成电路行业,提升工艺能力和水平显得尤为重要。以产品数据为来源和依据,对企业的工艺能力进行科学的分析,对于推动企业产品质量的提升必将起到至关重要的作用。 参考文献 [1]于万成,王桂莲.质量分析与控制技术常识[M].北京:高等教育出版社,2007:15-60. [2]贾新章,李京苑.统计过程控制和评价[M].北京:电子工业出版社,2004:15-63,138-143. Research on Process Capability in IC Enterprises Gong Wei, Zhou Jinyang (Dept.ofBiomedicalEngineering,ChangzhiMedicalCollege,ChangzhiShanxi046012,China) Abstract:Quantitative characterization and calculation method of process capability index for IC enterprises are discussed in this paper. The process capability of a concrete product is analyzed with the using of a kind of data analysis software of MiniData. Key words:process capability index; normal distribution; standard deviation 收稿日期:2016-01-23 作者简介:弓伟(1983- ),男,山西长治人,硕士研究生,工程师,研究方向:医疗电子设备。 通讯作者:周晋阳(1958- ),男,山西长治人,教授,研究方向:生物医学工程。 文章编号:1674- 4578(2016)03- 0074- 03 中图分类号:TN405 文献标识码:A