Curve let变换在X射线图像处理中的应用
刘艳华
(山西工程职业技术学院,山西 太原 030009)
Curve let变换在X射线图像处理中的应用
刘艳华
(山西工程职业技术学院,山西 太原 030009)
摘要:与其他算法相比,Curve let变换是一种更适合X射线图像特点的多尺度变换。它的基本表示元素是图像边缘,具有完备性和各向异性以及很强的方向性,能更好地对图像进行处理,尤其是在X射线图像处理中的作用也日益重要。文章首先简要介绍了Curve let变换的概念,随后详细叙述了Curve let 变换在图像处理中的应用。
关键词:Curve let变换;Ridge let变换;X射线图像;图像处理
目前,X射线成像应用十分广泛,但是现有X射线成像系统成像存在缺陷,系统内部存在噪声、成像质量差,现实中所采集到的X射线图像的背景噪声大且图像分辨率不高,因此我们就需要采用各种图像处理方法对采集到的X射线图像进行处理。Haar提出的小波变换被广泛地用于图像压缩、去噪、增强、特征提取、数字水印等[1]。在一维连续信号奇异性的描述上,小波变换存在很大的优势,而对二维图像中的边缘,如各种直线或者曲线等更高维的平面奇异性则难以表达其特征[2],且对于边缘方向的描述不是很准确。
为了弥补小波变换的不足,Donoho等提出了Curve let变换[2],它主要是将多尺度边缘作为其表达对象。Curve let变换的基本表示元素是图像边缘,具有完备性,能更好地满足图像处理的需要。另外Curve let变换的各向异性和很强的方向性也是X射线图像处理所需要的。
本文先介绍了Curve let变换的内容,随后重点介绍了Curve let变换在X射线图像处理中的应用。
1Curve let变换的概念
Curve let变换是一种由多尺度Ridge let变换和特殊的滤波过程组合而成的变换,其核心是Ridge let变换[3]。Curve let这种多尺度变换具有方向性,它可以将沿直线的奇异特性进行很好的描述,因此在对图像进行处理过程中,与其他方法相比,可以将图像的线性特征保护的较好。
下面我们首先简要介绍Ridge let变换,随后详细叙述Curve let变换的概念。
1.1Ridge let变换
二维连续Ridge let变换的定义为[4]:设光滑函数Ψ:R→R,符合以下条件:
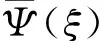
(1)
那么对任意的a>0,b∈R和θ∈[0,2π],将Ridge let的基函数ψ(abθ):R2→R2定义如下:
ψa,b,θ(x)=a-1/2·ψ((x1cosθ+x2sinθ-b)/a) .
(2)
则Ridge let变换定义为:
Rf(a,b,θ)=∫ψa,b,θ(x)f(x)dx .
(3)
其实,Ridge let变换是在Wavelet变换和Radon变换的基础上提出的。对函数f的Radon变换可以写成:
Rf(θ,t)=∫f(x1,x2)δ(x1cosθ+x2sinθ-t)dx1dx2.
(4)
其中,δ是单位脉冲函数,(θ,t)∈(0,2π)。由(3)式和(4)式,可以得到函数f的Ridge let变换为:
Rf(a,b,θ)=∫Rf(θ,t)a-1/2ψ((t-b)/a)dt .
(5)
在公式(5)中,θ是角度变量,它是个常数,而t是一个变量,它是沿角度θ的方向上变化的。由此可以看出在线性Radon变换切片上,Ridge let变换也可以称为是一维小波变换。
1.2Curve let变换
Curve let变换是一种基于Ridge let变换理论、多尺度Ridge let变换理论和带通滤波器理论的变换[5]。Curve let变换也可以说成是“Ridge let变换的积分”,它主要是由一组带通滤波器和多尺度的Ridge lets来完成的。多尺度的Ridge lets是指可以在一定尺度下按照一定长度和宽度进行分块的Ridge let,也可以把它看成是一种塔形结构,由一组加窗的Ridge let组成。通过带通滤波器组将目标函数f分解成从低频到高频的系列子带,以简化不同尺度下的计算过程[6]。图1详细描述了Curve let变换的实现过程。

图1 Curve let变换的实现过程
从图中可以看到,Curve let变换的核心部分是子带分解和Ridge let变换。首先,用子带分解算法分解原始图像,并对分解后的图像进行子带滤波;然后将不同的子带图像分成小块,再对每一小块图像进行Ridge let变换就到达了Curve let域。
2Curve let变换在X射线图像处理中的应用
2.1Curve let变换在图像降噪中的应用
Curve let变换对图像边缘的“稀疏”表示,则在确保均方误差比较低的同时,使图像数据的精简性和精确性达到了理想平衡,对图像边缘的精确表达仅需要较少的非零系数,在噪声环境下,它就体现出了很强的图像表达能力。
利用Curve let变换消除噪声的算法具体步骤如下[7]:
1) 利用Curve let变换对含噪声图像进行处理,获得各个子带的Curve let变换系数;
2) 采用阈值分析法对得到的Curve let变换系数进行处理。在Curve let变换中,较大的系数对应于较强的边缘,较小的系数则对应于噪声[8],因此就去除了较小的系数;
3) 将所保留的Curve let变换系数进行Curve let逆变换,就得到了消除噪声后的图像。

(a) 原始图像 (b) Curve let变换降噪后图像
实验结果如图2所示,由实验结果来看,经过Curve let变换降噪后的图像,图像的细节和纹理都有了比较清楚的显示,而且,图像的视觉效果也有了明显改善。
2.2Curve let变换在图像增强中的应用
对于X射线图像,采用Curve let变换进行图像增强,能够取得较好的增强效果,具体的图像增强过程如下[9]:
1) 将输入图像的标准噪声方差σ估算出来。
2) 将图像的Curve let系数计算出来,获得一系列子带ωj,每个子带ωj包含Nj个系数,和给定的分辨率是一一对应的。
3) 将每一个子带ωj中的标准噪声方差计算出来。
4) 求出每一个ωj中的最大值Mj,然后将Curve let变换的系数和y(|ωj,k|,σj)相乘。
5) 采用修正过的Curve let系数重建图像,也就完成了图像的增强。

(a) 原始图像(b) Curvelet变换图像
图3Curve let变换增强前后图像
从图3中可以看出,由Curve let增强算法增强后,图像的清晰度有了很大提高,可很清楚的看到32号丝,图像的背景噪声也得到了抑制。Curve let变换在图像增强方面的效果也显而易见了。
2.3Curve let变换在图像检索中的应用
由于Curve let变换在图像中层特征描述上具有很大优势,且能够较好的对图像的各向异性特征进行描述,因此,它在图像检索上也有很大的应用空间。Lei提出了一种基于Curve let特征的网络图像检索方法。图4为其检索过程。

图4基于Curve let的图像检索过程
2.4Curve let变换在图像压缩中的应用
Curve let对边缘具有较强的表达能力,也就是说采用较少的Curve let系数,就能够较好地重建富含边缘的图像[1]。可见,和小波变换相比,Curve let变换仅仅需要较少的系数就能够很好地完成原始图像的重建,这说明Curve let变换在指纹图像的压缩上具有很大的潜力。
另外,也可以直接采用Ridge let 变换对图像进行压缩,它主要是对序列图像的运动补偿帧差图像进行编码,形成一种小波变换与Ridge let变换相结合的混合算法,更好地完成图像的压缩。
3结束语
正是由于其多尺度和各向异性,使得Curve let变换在图像边缘的描述及合成上有很广阔的应用空间,在对比度的增强和背景噪声的抑制上,在图像去噪以及增强方面明显的优于小波变换。经过近几年的发展,Curve let变换在图像背景的杂波抑制以及其他图像处理领域都发挥了重要作用,弥补了小波变换的不足,显示出了其优越性。
参考文献
[1]倪林,Miao Y.一种更适合图像处理的多尺度变换——Curve let变换[J].计算机工程与应用,2004,28:21-26.
[2]Cands E J,Donoho D L.Curvelet[R].USA:Department of Statistics,Stanford University,1999.
[3]李智杰,高新波,姬红兵.基于Curvelet变换的红外图像背景杂波抑制算法[J].红外技术,2004,26(5):1-4.
[4]Emmanuel J,Candes,David L.Donoho.Ridgelets:The Key to High-Dimensional Intermittency[J].Phil Trans R Soc Lond A,1999,357:2495-2509.
[5]Jean-Lue Starck,Emmanuel J.Candes,David L.Donoho.The Curvelet Transform for Image Denoising[J].IEEE Trans on Image Processing,2002,11(6):670-684.
[6]Emmanuel J,Candes,David L.Donoho.Curvelets-A Surprisingly Effective Nonadaptive Representation for Objects with Edges[A].Saint-Malo Proceeding,1999.Curve and Surface Fitting[C],IV:1-16.
[7]刘广东,陈阿林.基于Curvelet变换的图像去噪[J].重庆师范大学学报(自然科学版),2009,26(4):86-89.
[8]阎敬文,屈小波.超小波分析及应用[M].北京:国防工业出版社,2001.
[9]刘艳华,程耀瑜,张向兵.基于Curve let变换的X射线图像增强算法的研究[J].无损检测,2010(4):253-255.
The Application of Curve Let Transform in X-ray Image Processing
Liu Yanhua
(ShanxiEngineeringVocationalCollege,TaiyuanShanxi030009,China)
Abstract:Compared with other algorithms, Curve let transform is a multi-scale transform which more suits to the characteristics of the X-ray image. It makes the edge for the basic elements and has the features of completeness, anisotropy and very strong directivity, which can better deal with image, especially the role of X-ray image processing is also increasingly important. This paper gives the Curve let transform concepts, then summarizes the Curve let transform application in image processing.
Key words:Curve let transform; Ridge let transform; X-ray image; image processing
收稿日期:2016-01-15
作者简介:刘艳华(1985- ),女,河南周口人,助教,硕士研究生,主要研究方向:X射线实时成像以及图像处理、电工电子技术等。
文章编号:1674- 4578(2016)03- 0005- 02
中图分类号:TP391
文献标识码:A

