拓宽加固结构荷载横向分布计算研究

李　智， 郑　利

(1.湖南省高速公路管理局， 湖南 长沙　410005；　2.辰溪县公路管理局， 湖南 辰溪　419500)



拓宽加固结构荷载横向分布计算研究

李智1， 郑利2

(1.湖南省高速公路管理局， 湖南 长沙410005；2.辰溪县公路管理局， 湖南 辰溪419500)

摘要：采用纵横梁拓宽加固的桥梁，加宽主梁与原主梁刚度不等，常用的荷载横向分布计算方法不适用于此类结构，为此，对纵横梁拓宽加固后桥梁荷载横向分布的计算问题进行研究，采用不等刚度荷载横向分布计算理论和有限元建模计算，分别按不等刚度荷载横向分布理论和有限元方法计算拓宽加固结构的横向分布影响线，经比较两种方法的计算结果，确定了拓宽加固结构的荷载横向分布计算方法，为同类工程计算提供了方便。

关键词：空心板桥； 纵横梁拓宽加固； 不等刚度梁； 荷载横向分布计算； 有限元方法

0引言

为了满足道路加宽与荷载等级提高的要求，采用在原桥左右两侧各增加一道纵梁，在纵梁下部加设横梁，将原桥“托起”，形成的纵横梁拓宽加固技术[1]，这种方法由于施工简单、受力明确备受大家关注。然而，拓宽加固后，边梁与中梁刚度不等，边梁刚度更大，且同时有横梁作用，如何计算这种拓宽加固结构的横向分布问题，是桥梁加固计算中一个重要内容。由于这种加固技术并不常见，国内外对此类问题的研究少见报道，但有学者针对边梁刚度不等问题的有研究，提出“大边梁”的刚度换算方法[2]。本文针对空心板桥拓宽加固的工程实际，采用有限元建模计算和理论分析计算，两种方法比较，提出空心板桥拓宽加固时荷载横向分布计算方法。

1空心板桥拓宽加固结构荷载横向分布特征

采用纵横梁拓宽加固技术加固的空心板桥梁，如图1，由于结构的空间整体性，当桥上作用外荷载时，各片主梁将共同参与受力，这就形成了各片主梁之间的内力分布。每片主梁分布到的内力的大小，随主梁刚度、桥梁结构以及荷载作用位置的不同而不同，拓宽加固中必须准确的计算结构的受力。按照不等刚度梁的荷载横向分布计算理论，分

图1　纵横梁拓宽加固空心板桥横截面示意图

“二次”计算，然后叠加。

2不等刚度荷载横向分布理论

针对工程实践中的不等刚度梁的荷载横向分布计算问题，学者提出了“大边梁”的计算方法。

2.1不等刚度荷载横向分布基本原理

不等刚度荷载横向分布系数计算方法，也称为带“大边梁”荷载横向分布计算法[2]，它首先将刚度较大主梁的刚度分为两部分，一部分刚度与较小主梁刚度相等，超出较小刚度主梁的刚度部分则视为在梁底施加“弹性支承”刚度，计算时先按等刚度主梁计算横向分布，再将多余刚度看作“弹性支承”，将“弹性支承力”作为未知反力来求解，并求出“弹性支承力”对横向分布的影响量，然后将结果进行叠加，即可得到荷载横向分布影响线竖标值。它一般适用于边梁刚度较中部主梁大出较多的桥梁荷载横向分布的计算，而这一条件刚好符合纵横梁拓宽加固结构的特点。

2.2不等刚度荷载横向分布计算

不等刚度荷载横向分布计算分两部分，一部分与等刚度梁的计算相同，超出主梁刚度部分则需另外考虑，然后再将这两部分引起的荷载横向分布叠加即可。第一部分计算不再赘述，超出部分计算如下：

由文献[3]的推导可知超出刚度部分引起的荷载横向分布计算公式如下：

A边梁处的荷载横向分布计算公式为：

(1)

B边梁处的荷载横向分布计算公式为：

(2)

中梁荷载横向分布计算公式为：

(3)

(4)

(5)

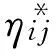
3不等刚度法与有限元计算对比

为了研究不等刚度荷载横向分布计算理论在纵横梁拓宽加固结构荷载横向分布计算中的适用性，本文以某13 m跨径预应力空心板桥为例，进行拓宽加固计算，采用不等刚度法和有限元模型分别对加固后桥梁荷载横向分布进行计算。

3.1工程概况

某标准跨径为13 m的预应力砼空心板桥，共有8块空心板，板与板之间横向联系采用铰接。进行纵横梁拓宽加固时，在原桥两边各设置一道纵梁，并在纵梁之间设置一道横梁。纵横梁拓宽加固空心板截面示意图如图1，原桥空心板截面如图2，拓宽加固的两个边梁采用T梁截面示意图如图3a，连接两片纵梁的横梁截面如图3b。

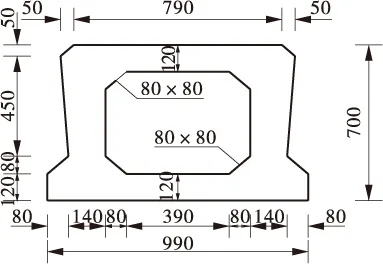
图2　原桥空心板截面(单位： mm)

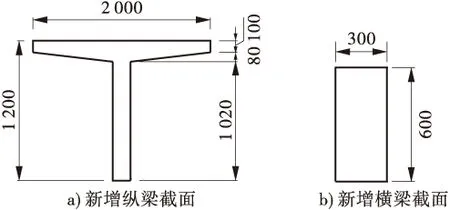
图3　新增纵梁和横梁截面(单位： mm)

3.2不等刚度法计算横向分布影响线

计算纵横梁拓宽加固结构荷载横向分布时，先按等刚度进行计算，等刚度条件下荷载横向分布影响线竖标值在文献[4]中查表即可得到。对于超出部分刚度作用下的影响线竖标值，首先应计算出刚度比，然后再根据式(1)～式(5)进行计算即可得到相应的影响线竖标值。再将以上两部分结果进行叠加，现计算了1号梁、3号和5号板的荷载横向分布影响线，如图4。

图4　荷载横向分布影响线

3.3有限元法计算

利用空间有限元分析软件Midas/Civil计算纵横梁拓宽加固后的桥1号梁、3号和5号板的荷载横向分布情况，有限元模型如图5。

图5　纵横梁拓宽加固有限元模型

计算得到的1号梁、3号和5号板的荷载横向分布影响线如图6。

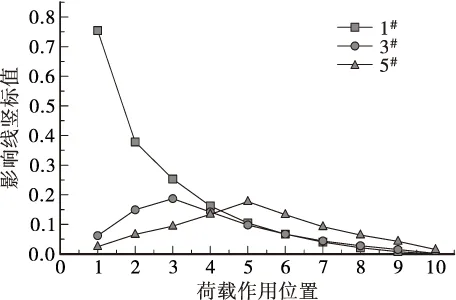
图6　荷载横向分布影响线

3.4结果对比分析

将2种方法计算所得结果绘于同一图中，如图7所示，其中带点标号表示有限元计算结果。

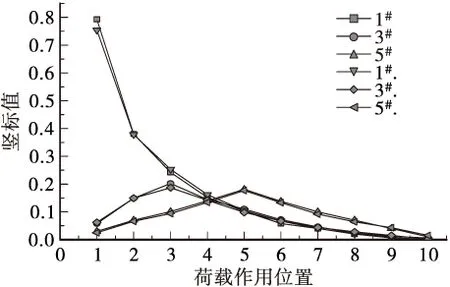
图7　荷载横向分布影响线对比图

对比两种计算方法所得的横向分布影响线可以直观的看出，以不等刚度计算法计算所得的纵横梁拓宽加固后桥梁的荷载横向分布影响线与有限元计算结果较为吻合，说明不等刚度荷载横向分布计算法能够用于纵横梁拓宽加固空心板桥结构荷载横向分布影响线的计算。尽管只计算了空心板桥，但该方法源自于T梁刚度不等的荷载横向分布计算，因此，“大边梁”的横向分布计算理论同样适用于拓宽加固空心板桥、T梁桥的计算。

4结论

本文针对纵横梁拓宽加固空心板桥梁的实际特点，引入了不等刚度计算法计算纵横梁拓宽加固后桥梁的荷载横向分布，并将其与有限元计算结果进行对比，两种计算方法所得结果较为吻合，说明不等刚度荷载横向分布计算方法适用于纵横梁拓宽加固空心板桥、T梁桥结构荷载横向分布的计算，为桥梁加固的设计计算提供依据。

参考文献：

[1] 李黎明.混凝土桥梁拓宽加固研究[D].长沙:长沙理工大学,2015.

[2] 范立础.桥梁工程[M].北京:人民交通出版社，1987.

[3] 张元海,李乔.带大边梁的桥梁结构实用空间的虚拟纵梁法[J].工程力学,2008,25(7):185-195.

[4] 李国豪.公路桥梁荷载横向分布计算[M].北京:人民交通出版社，1987.

[5] 包龙生,于玲,周晓丹. 大边梁加固旧桥的模型试验研究[J].东北公路,2003,26(2):105-108.

[6] 贺栓海, 谢仁物.公路桥梁荷载横向分布计算方法[M].北京:人民交通出版社，1996.

[7] K.M.Tarhini ,G.R. Frederick. Lateral load distribution in I-girder bridges[J]. Computers & Structures,2000,54(2):351-354.

[8] 黄平明,姜从礼,龚明泉.梁桥的大边梁加固法研究[J].西安公路交通大学学报,1999,19(4): 22-23.

[9] 陈记豪,赵顺波,姚继涛.既有预应力空心板桥加宽设计的荷载横向分布计算方法[J].工程力学，2012,29(9):265-271.

[10] 秦清波,何雄军,朱琳.简支梁(板)桥加固改造形式研究[J].公路交通科技,2006(4):106-108.

[11] 张建仁,刘小燕.结构设计原理[M].北京:人民交通出版社,2015.

[12] 邱顺东.桥梁工程软件midas Civil应用工程实例[M].北京:人民交通出版社，2011.

文章编号：1008-844X(2016)02-0160-03

收稿日期:2016-04-13

作者简介:李智( 1981-) ，男，工程师，主要从事高速公路建设管理。

中图分类号：U 448.21+2

文献标识码：A