赤石大桥下拉索施工抗风措施风致振动响应分析

王　海

(湖南海纳沐舟建设有限公司， 湖南 长沙　410000)



赤石大桥下拉索施工抗风措施风致振动响应分析

王海

(湖南海纳沐舟建设有限公司， 湖南 长沙410000)

摘要：以赤石特大桥为工程依托，针对赤石大桥施工抗风措施“下拉索+TMD”中的下拉索在大风条件下可能产生的大幅振动问题，采用ANSYS软件进行考虑全桥结构的下拉索风致抖振响应分析。计算结果表明：采取施工抗风措施且考虑下拉索脉动风效应后(斜拉索分段建模)，最大双悬臂状态桥塔关键截面和主梁塔梁交界处截面应力均满足规范要求，即下拉索脉动风效应不会对桥塔、主梁结构抗风安全产生明显不利的影响；考虑下拉索脉动风效应(且拉索分段建模后)，下拉索最大索力值为1.091E+06 N，比单索模型结果偏小约20%左右；下拉索中点顺桥向、横桥向风致抖振位移响应极大值分别为2.94 m和3.44 m。

关键词：赤石大桥； 斜拉桥； 下拉索； 平均风特性； 脉动风特性

0引言

高墩大跨斜拉桥施工期风致振动问题是大跨度斜拉施工中至关重要问题之一，在工程实践中受到广泛关注，工程实践中大跨斜拉桥施工期风致振动控制措施主要有下拉索和调谐质量阻尼器(tuned mass damper，TMD)两大类措施[1，3]。如德国Kine桥(主跨320 m，主跨钢结构，边跨混凝土梁，1969年建成)在施工过程中在主梁下侧临时增设了横撑，以提高主梁的抗扭刚度，进而消除颤振发生的可能性；上世纪80年代中期，加拿大Annacis桥上首次采用下拉索抗风措施来提高结构基频，从而减小结构风致抖振响应。法国米约大桥在方案设计阶段曾考虑采用平衡悬臂施工法，并研究了下拉索抗风措施的可行性问题，后来该桥采用顶推法施工，建造了7个钢桁架临时塔架以实现主梁的顶推，同时兼顾提高大桥施工期抗风性能。韩国釜山—巨济(Busan-Geoje)联络线中的两座斜拉桥(Lot1和Lot2)在风洞试验研究中发现在最大双悬臂施工阶段梁端可能会出现较大的竖向风致振动响应，从而引起较大的风荷载，故分别进行了“下拉索”和“TMD”控制措施研究，最后考虑方案的可行性，由于该桥为跨海桥梁，故最后采取TMD控制措施进行大桥风致振动控制。本文以在建的赤石特大桥为工程依托，考虑到赤石大桥施工抗风措施中下拉索距离桥面高度较大(约180 m左右)，在脉动风作用下下拉索可能会发生一定振幅的风致抖振响应。故考虑下拉索脉动风效应，针对施工抗风措施(下拉索+TMD措施)的大桥双悬臂施工阶段桥塔关键截面的应力进行验算，并对下拉索风致振动响应进行计算，以评估下拉索风致振动对大桥的抗风安全的影响。

1工程概况

赤石特大桥位于厦门至成都国家高速公路湖南省汝城至郴州公路段，主桥结构为(165+3×380+165)m=1 470 m的四塔五跨预应力混凝土斜拉桥，采用边塔对主梁提供竖向、横向支承、中塔塔-梁-墩固结结构体系，边中跨之比为0.434 2。主桥各塔每侧均布置23对斜拉索，拉索纵向呈扇形布置，主桥结构总体布置图见图1。主梁为单箱四室混凝土箱梁，桥宽为28.0 m，梁高为3.2 m。5#～8#塔塔高分别为246.63、274.13、286.63、266.13 m，桥面距离桥下河床的距离约为180 m左右，拉索采用钢绞线斜拉索。鉴于大桥结构特点(曲线高塔、高桥面、双悬臂施工、混凝土主梁)和工程规模，大桥施工期的风致振动问题应予以足够的重视。

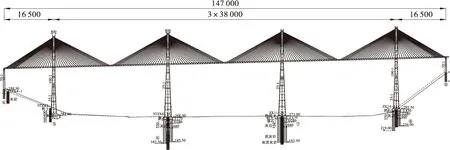
图1　赤石大桥主桥结构总体布置图(单位： cm)

2结构有限元模型

为了合理评估下拉索风致振动对大桥的抗风安全和下拉索自身的风致振动效应问题，特建立包含下拉索的全桥结构有限元模型。采用大型有限元结构分析程序ANSYS建立大桥结构有限元模型，采用空间梁单元BEAM4模拟主梁、桥塔等结构，采用LINK10模拟斜拉索、下拉索等结构，采用Ernst公式考虑斜拉索的垂度效应，采用MASS21质量单元模拟桥面压重、施工挂篮等质量。为了考虑下拉索的风致振动响应，将各下拉索划分成10个单元，分别在各下拉索节点处模拟脉动风速，并采用抖振分析理论进行脉动风荷载计算，将该脉动风荷载与桥梁桥塔、主梁脉动风荷载同步施加到结构上，进行抖振响应时域分析。在进行时域分析时，考虑了结构自重、初始索力等因素，并计入了几何非线性效应。图2所示为赤石大桥7号塔考虑下拉索的结构有限元模型。

图2　赤石大桥7号塔最大双悬臂结构有限元模型　　　(考虑下拉索)

3桥梁结构抖振响应分析方法

采用谐波合成法生成桥梁主梁和桥塔上关键节点脉动风速，采用大型有限元分析软件ANSYS对赤石大桥最大双悬臂状态原结构和采取施工抗风措施状态进行抖振响应分析。采用Davenport准定常抖振理论进行主桥结构最大双悬臂状态抖振响应计算，采用ANSYS中的MATRIX27实现桥梁自激力的模拟。

3.1脉动风速模拟

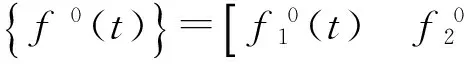
(1)

式中：j为所要模拟的空间场点数；N为一个充分大的正整数；Δω=ωu/N为频率增量；ωu为上限截止频率，即当ω>ωu时，互谱密度矩阵S0(w)=0；ωml为双索引频率；φml为均匀分布在(0，2π)区间的随机相位；Hjm(ωml)是矩阵[H(ω)]的元素。

其互谱密度矩阵为：

S0(ω)=S011(ω)S012(ω)…S01n(ω)S021(ω)S022(ω)…S02n(ω)…………S0n1(ω)S0n2(ω)…S0nn(ω)éëêêêêêêêêêùûúúúúúúúúú

(2)

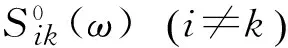
按照Cholesky分解法，正定的Hermitian矩阵S0(ω)可以分解为：

S0(ω)=H(ω)HT*(ω)

(3)

其中，H(ω)是下三角矩阵；HT*(ω)是其复共轭转置矩阵。

谐波合成法利于谱分解和三角级数叠加来模拟随机过程，水平和竖向脉动风速谱分别取与风洞实验拟合较好的Simiu谱和Panofsky谱。图3为某节点脉动风速时程和功率谱密度曲线，可以看出，所模拟的脉动风速风谱与目标风谱吻合较好。

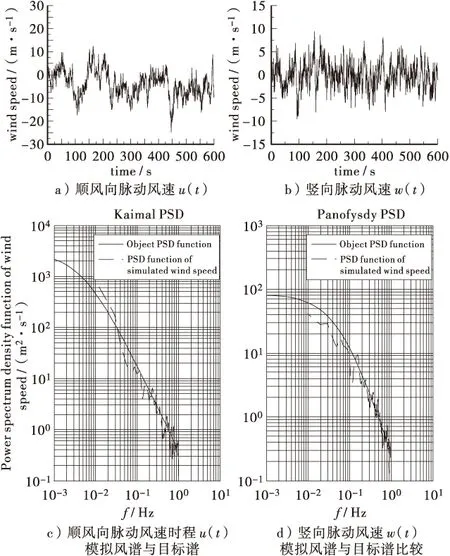
图3　某节点脉动风速时程与功率谱密度曲线

3.2抖振力计算

自然风中紊流在桥梁结构单位长度主梁上的抖振力可表示为：

Fyb(t)=ρUAnCDu(t)+

Fzb(t)=ρUBCLu(t)+

(4)

作用在单位长度主梁上的自激力可表示为：

(5)

其中，C0为气动阻尼矩阵；K0为气动刚度矩阵；δ为单元位移向量。

单元气动阻尼矩阵为：

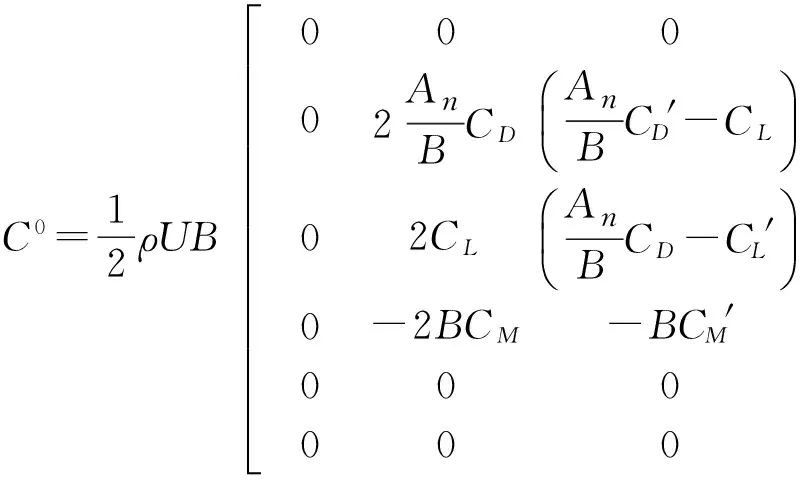
C0=12ρUB00002AnBCDæèçAnBCD'-CLöø÷02CLæèçAnBCD-CL'öø÷0-2BCM-BCM'000000éëêêêêêêêêêêê

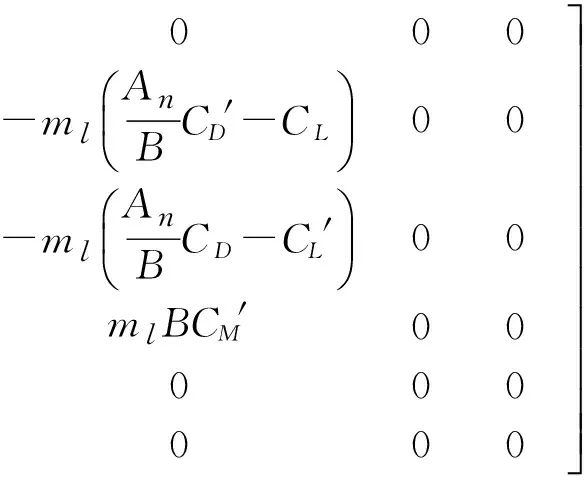
000-mlæèçAnBCD'-CLöø÷00-mlæèçAnBCD-CL'öø÷00mlBCM'00000000ùûúúúúúúúúúúú

(6)

单元气动刚度矩阵为：

K0=12ρU2B000000000AnBCD'00000CL'00000-BCM'00000000000000éëêêêêêêêêêêùûúúúúúúúúúú

(7)

现将单元单位长度自激力转化为单元两端的节点力，则单元节点集中力可表达为：

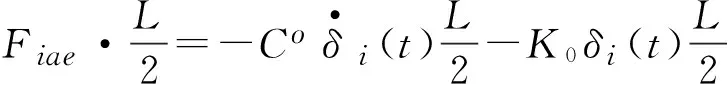
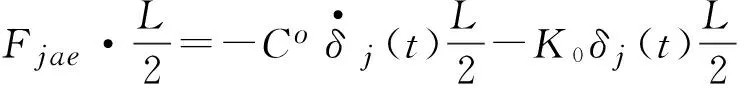
(8)

其中，L为单元长度。

将上式写成矩阵形式，即可得作用于单元节点的气动刚度和气动阻尼矩阵，即：

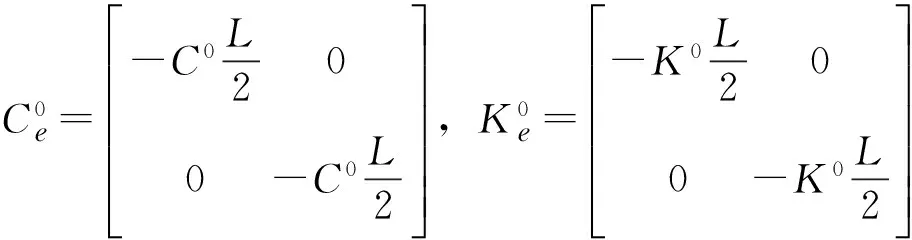
C0e=-C0L200-C0L2éëêêêêêùûúúúúú,K0e=-K0L200-K0L2éëêêêêêùûúúúúú

(9)

忽略桥塔、下拉索自激力的作用，仅考虑脉动风的作用，故单位长度桥塔截面、下拉索的抖振力可按下式计算，即：

(10)

式中：Fst为结构的静风力；Fb(t)为结构的抖振力；ρ为空气密度；CD为桥塔塔柱截面(或下拉索)的阻力系数；D为桥塔截面迎风面的宽度(或下拉索直径)；u(t)为顺风向脉动风速。

4计算结果

图4为7#塔下拉索索力时程曲线，从图4中可看出，考虑下拉索的脉动风效应后(且拉索分段后)，下拉索的最大索力值为1.091E+06 N(比单索模型结果偏小约20%左右，A～H为下拉索编号)，图5所示为主梁悬臂端竖向位移时程曲线。表1 所示为对称风作用下7#塔对应最大双悬臂状态考虑下拉索脉动风效应抖振响应结果汇总。

桥塔和主梁结构主要承受轴力、弯矩、剪力和扭矩作用，故对桥塔和主梁关键截面位置的正应力、主拉应力以及桥塔关键截面扭矩承载力进行验算。静阵风荷载效应与抖振响应结果组合见表1，对应的桥塔和主梁关键截面角点应力见表2。从表2中可以看出，桥塔关键截面正应力均为压应力，满足规范要求。

图4　赤石大桥7#塔双悬臂状态下拉索索力时程曲线(考虑下拉索脉动风效应)

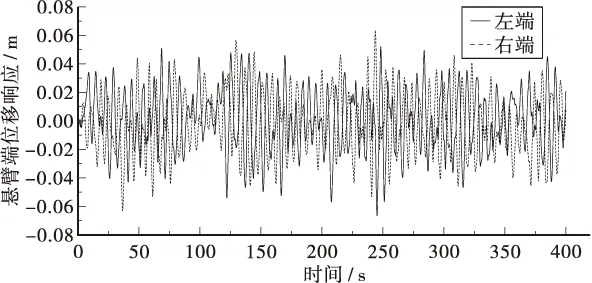
图5　赤石大桥7#塔双悬臂状态主梁悬臂端竖向位移时程曲线(考虑下拉索脉动风效应)

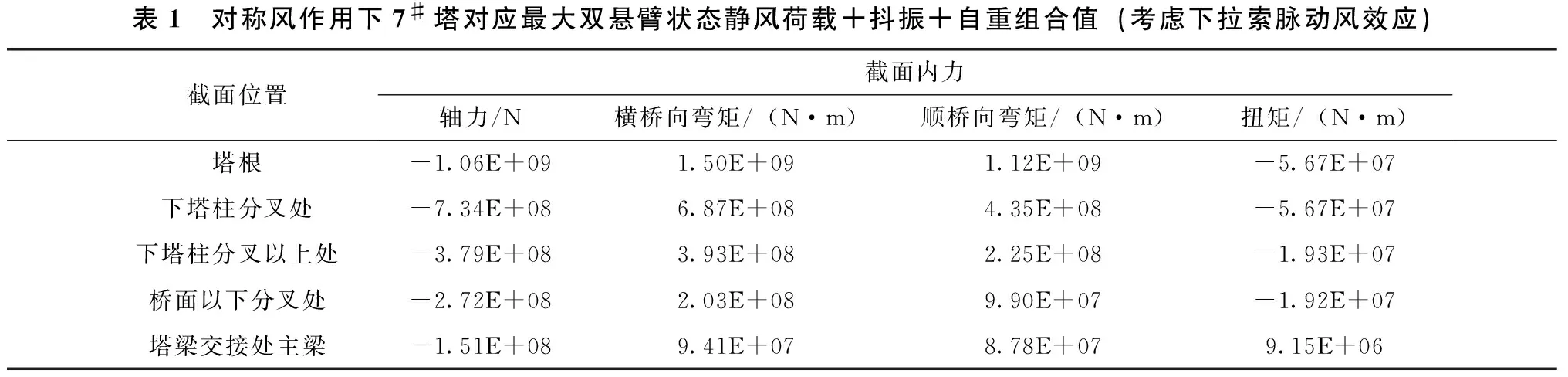
表1 对称风作用下7#塔对应最大双悬臂状态静风荷载+抖振+自重组合值(考虑下拉索脉动风效应)截面位置截面内力轴力/N横桥向弯矩/(N·m)顺桥向弯矩/(N·m)扭矩/(N·m)塔根-1.06E+091.50E+091.12E+09-5.67E+07下塔柱分叉处-7.34E+086.87E+084.35E+08-5.67E+07下塔柱分叉以上处-3.79E+083.93E+082.25E+08-1.93E+07桥面以下分叉处-2.72E+082.03E+089.90E+07-1.92E+07塔梁交接处主梁-1.51E+089.41E+078.78E+079.15E+06

表2 桥塔、主梁关键截面位置正应力(考虑下拉索脉动风效应)截面位置截面角点正应力/PaABCD塔根-4.57E+06-6.95E+06-7.10E+06-9.48E+06下塔柱分叉处-3.08E+06-5.69E+06-5.51E+06-8.12E+06下塔柱分叉以上处-1.29E+06-8.52E+06-4.30E+06-1.15E+07桥面以下分叉处-1.68E+06-3.74E+06-2.35E+06-4.41E+06塔梁交接处主梁-1.11E+06-1.08E+07-2.75E+06-1.24E+07 注:截面角点A～D分别对应桥塔关键截面的4个角点。

图6所示为下拉索风中点位置沿顺桥向和横桥向振动位移时程曲线，图7所示为其中1#索中点位置风致振动轨迹曲线。表3所示为7#对应下拉索位移响应统计极值。从表3中可以看出，下拉索中点顺桥向、横桥向的位移极大值分别为2.94 m和3.44 m。

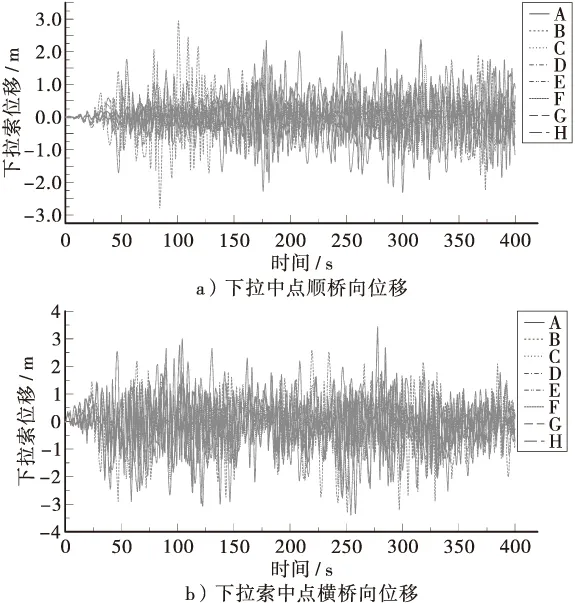
图6　下拉索中点顺桥向、横桥向位移时程曲线

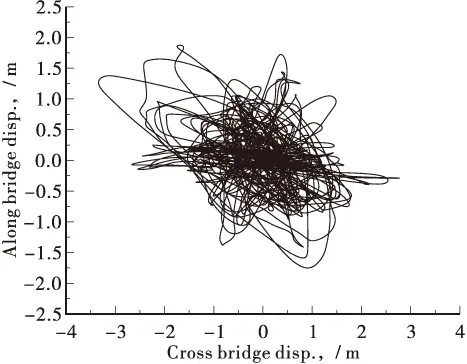
图7　7#塔下拉索1#索中点位移轨迹曲线

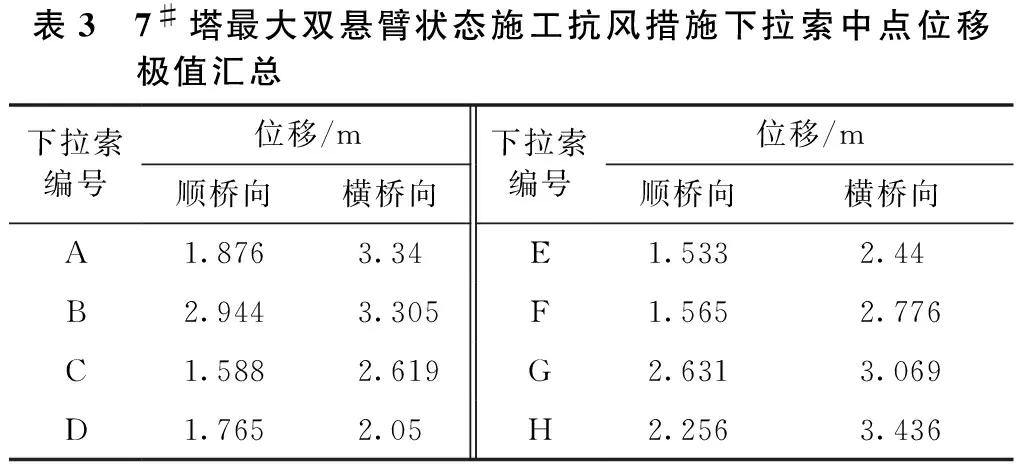
表3 7#塔最大双悬臂状态施工抗风措施下拉索中点位移极值汇总下拉索编号位移/m顺桥向横桥向下拉索编号位移/m顺桥向横桥向A1.8763.34E1.5332.44B2.9443.305F1.5652.776C1.5882.619G2.6313.069D1.7652.05H2.2563.436

5结论

通过对赤石大桥下拉索风致振动效应有限元分析，可以得到如下主要研究结论：

1)采取施工抗风措施，且考虑下拉索脉动风效应后(斜拉索分段建模)，最大双悬臂状态桥塔关键截面和主梁塔梁交界处截面应力均满足规范要求，即下拉索脉动风效应不会对桥塔、主梁结构抗风安全产生明显不利的影响。

2) 考虑下拉索脉动风效应(且拉索分段建模后)，下拉索最大索力值为1.091E+06 N，比单索模型结果偏小约20%左右。

3) 下拉索中点顺桥向、横桥向风致抖振位移响应极大值分别为2.94 m和3.44 m。

参考文献：

[1] JTG/T D60-01-2004，公路桥梁抗风设计规范[S].

[2] 湖南大学风工程与桥梁工程湖南省重点实验室.汝(城)至郴(州)高速公路赤石特大桥施工抗风措施研究报告[R].2014.

[3] 陈艾荣，顾明，项海帆.调质阻尼器对斜拉桥竖向抖振控制的试验研究[J].西安公路学院学报，1993，13(2)：8-13.

[4] Aas-Jakobsena K，Strommen E.Time domain buffeting response calculations of slender structures[J].Journal of Wind Engineering & Industrial Aerodynamics，2001，89：341-364.

文章编号：1008-844X(2016)02-0124-04

收稿日期:2016-03-14

作者简介:王海( 1981-) ，男，工程师，主要从事路桥建设管理。

中图分类号：U 448.27

文献标识码：A