堆积碎石土斜坡浅表现场入渗试验研究
李园园, 董 辉, 刘运思
(1.湖南省高速公路管理局, 湖南 长沙 410001; 2.湘潭大学 土木工程与力学学院, 湖南 湘潭 411105;3.湖南科技大学 土木工程学院, 湖南 湘潭 411201)
堆积碎石土斜坡浅表现场入渗试验研究
李园园1, 董辉2, 刘运思3
(1.湖南省高速公路管理局, 湖南 长沙410001;2.湘潭大学 土木工程与力学学院, 湖南 湘潭411105;3.湖南科技大学 土木工程学院, 湖南 湘潭411201)
摘要:为探究强降雨下堆积体斜坡浅表入渗规律,通过自制双环入渗仪分别对堆积碎石土饱和导水率和不同深度土层含水率进行现场试验,对堆积碎石土斜坡渗透特性在不同位置的空间变异性进行了研究。研究结果表明:测试区碎石土现场入渗过程符合Kostiakov模型;饱和导水率在南北方向(斜坡长轴方向)、东西方向以及坡顶、坡腰、坡脚区域的空间变异性均属于中等变异,坡表含水率在空间整体分布下变异系数相对较大(中等变异),而在垂直方向水分分布的变异程度相对较小(弱变异);堆积碎石土入渗速率从坡顶到坡脚呈现出相对减小的趋势;坡脚、坡腰平均含水率相对较高(12%~15%),坡顶平均含水率相对较少(9%~10%),坡表平均含水率沿垂直方向随着地层深度增加先增加后减小,在距地表10~15 cm深度范围含水率最大。
关键词:斜坡; 堆积碎石土; 双环入渗试验; Kostiakov模型; 空间变异
0引言
堆积碎石土是风化卸荷等复杂成因形成的介于土体和破裂岩体间的特殊地质体。其作为坡体物质分布于我国西北及西南部。在国内发生的滑坡类型中,堆积体滑坡所占比例很大,具有影响范围广、爆发频率多、持续危害大等特点[1]。堆积碎石土作为堆积体滑坡的滑体物质具有透水性强、大孔隙性、粒径范围广等特点,极易在强降雨条件下诱发滑坡灾害[2]。因此,探究土体的入渗规律对预防滑坡、泥石流等灾害研究具有一定理论影响。
由于堆积碎石土物质组成复杂、结构排列无序,其入渗规律难以确定。目前,国内外学者为探求碎石土入渗规律,综合运用了室内试验、理论推导及数值模拟等方法进行了一系列研究。杨艳芬等[3]为研究碎石粒径大小和碎石率对碎石土入渗规律的影响,通过室内一维入渗试验,验证了在碎石土碎石含率中存一个阈值影响湿润锋迁移速率以及累积入渗量,且随碎石土级配的变化阈值发生改变。董辉等[4]结合Wang等[5]提出的考虑气体影响的修改Green-Ampt入渗模型,通过室内入渗试验及数值模拟分析,考虑了堆积碎石土内空气阻力对其入渗规律的影响,得到了气阻作用下堆积碎石土渗流规律。周中等[6]利用正交实验的方法,通过自制常水头渗透仪,测定了土石混合体的渗透系数,并且分析不同因素(含石量、孔隙比和颗粒形状)对土石混合体渗透系数的影响,确定每种因素对土石混合体渗透系数影响大小。许建聪等[7]采用数理统计分析方法对碎石土的渗透特性进行研究,得出以粉粒和黏粒为主的细粒土粒组的含量对碎石土渗透系数影响最大。由于现场试验所需耗费太高,试验开展困难,目前关于堆积碎石土现场入渗试验的相关研究相对较少,但原位入渗试验能减少对原状土体扰动,且更真实地反映碎石土的入渗规律。
为此,本文通过对湘水竹湾隧道出口处堆积碎石土边坡进行实地双环入渗试验,通过对该斜坡处碎石土渗透特性在不同位置和方向的变异进行了较系统的分析研究。该结果不仅对研究降雨引起滑动变形的动态机制,还为深入探求滑坡启动预报模型提供试验依据。
1野外碎石土入渗试验
1.1仪器研制
为减少原状土体扰动区域,同时弱化尺寸效应对堆积碎石土斜坡上入渗试验的影响,本文设计了自制双环入渗仪,分别由恒压供水装置、入渗发生装置及支撑测量装置组成(见图1)。入渗发生装置采用大直径圆环(内外环直径分别为35 cm、50 cm),既保证了合适的内外径比且减少了尺寸效应对入渗速率的影响[8]。马氏瓶作为恒压供水装置可分别为内外环供水。设计通过调整普通马氏瓶补水阀、进气阀和加水阀的位置,使供水装置补水连续、反应灵敏、操作简单。为了既减少斜坡坡表区域扰动范围又确保各测试点供水压力统一且可调,本文通过在斜坡上架设三脚架作为供水装置的支撑从而减少整平场地的面积,三脚架亦能精确调节马氏瓶的高度,从而保证各试验点供水压力统一。同时,试验还利用电子称测量马氏瓶内水的含量从而换算出不同时刻环内水的累积入渗量。该方法不但读数方便而且较常规方法提高了累积入渗量的测量精度。

图1 自制双环入渗仪
1.2研究内容
试验区域为长约40 m宽约6 m的湘潭市水竹湾隧道出口处堆积碎石土边坡。试验主要内容为:① 通过GPS定位技术对边坡进行地形测量获取地形信息,并按照2 m×8 m方格网共18个测试点,即边坡坡脚、坡腰、坡顶处各布设6个试验点(见图2); ②根据试验规程[9]对18个试验点运用自制双环入渗仪进行碎石土饱和入渗试验,记录不同时间环内水的累积入渗量,且测量试验水温对入渗率进行温度修正[10]; ③入渗试验结束后(历时90 min)立即用洛阳铲对试验点碎石土进行采样,并运用烘干法分别测出试验点不同深度(0~5 cm、5~10 cm、10~15 cm、15~20 cm、20~25 cm)堆积碎石土的含水率。为了确保含水率测定的精确性,对每个试验点在不同位置分别取3组样点求平均值。

图2 试验点布置
2结果与分析
2.1碎石土入渗公式优选
据研究成果[11]可知,Philip模型[12]与Kostiakov模型[13]的实用性强,在入渗计算过程中应用广泛。其中两个入渗模型公式如下:
Philip模型:
I(t)=St0.5+At
(1)
式中:I为单位面积累积入渗量,cm;t为时间,min;S为土壤吸渗率,cm/min;A为稳渗率,cm/min。
Kostiakov模型:
(2)
式中:k为入渗系数,cm/min;α为经验入渗指数。
因此,利用上述两个模型对18个测点入渗数据进行拟合,将相关系数与均方根误差作为评价依据进行入渗公式优选,确定各点入渗速率,结果见表1。为验证优选模型是否具备普适性,同时在斜坡研究区域之外随机取6个测试点进行入渗试验并将入渗数据与研究区域入渗数据进行对比分析。
由表1可知,研究区域内(18个试验点)各测试点应用Philip公式的相关系数(R2)均比利用Kostiakov公式拟合要小,而Philip公式的均方根误差(RMSE)却比Kostiakov公式要大。同时,在研究区域外随机选取的6个试验点应用Kostiakov公式也比Philip公式更接近实测入渗数据曲线。由此可知,对于堆积碎石土而言,采用Kostiakov公式描述其入渗过程效果较好且具有一定普适性,即可将温度修正后的入渗系数视为堆积碎石土的入渗率。
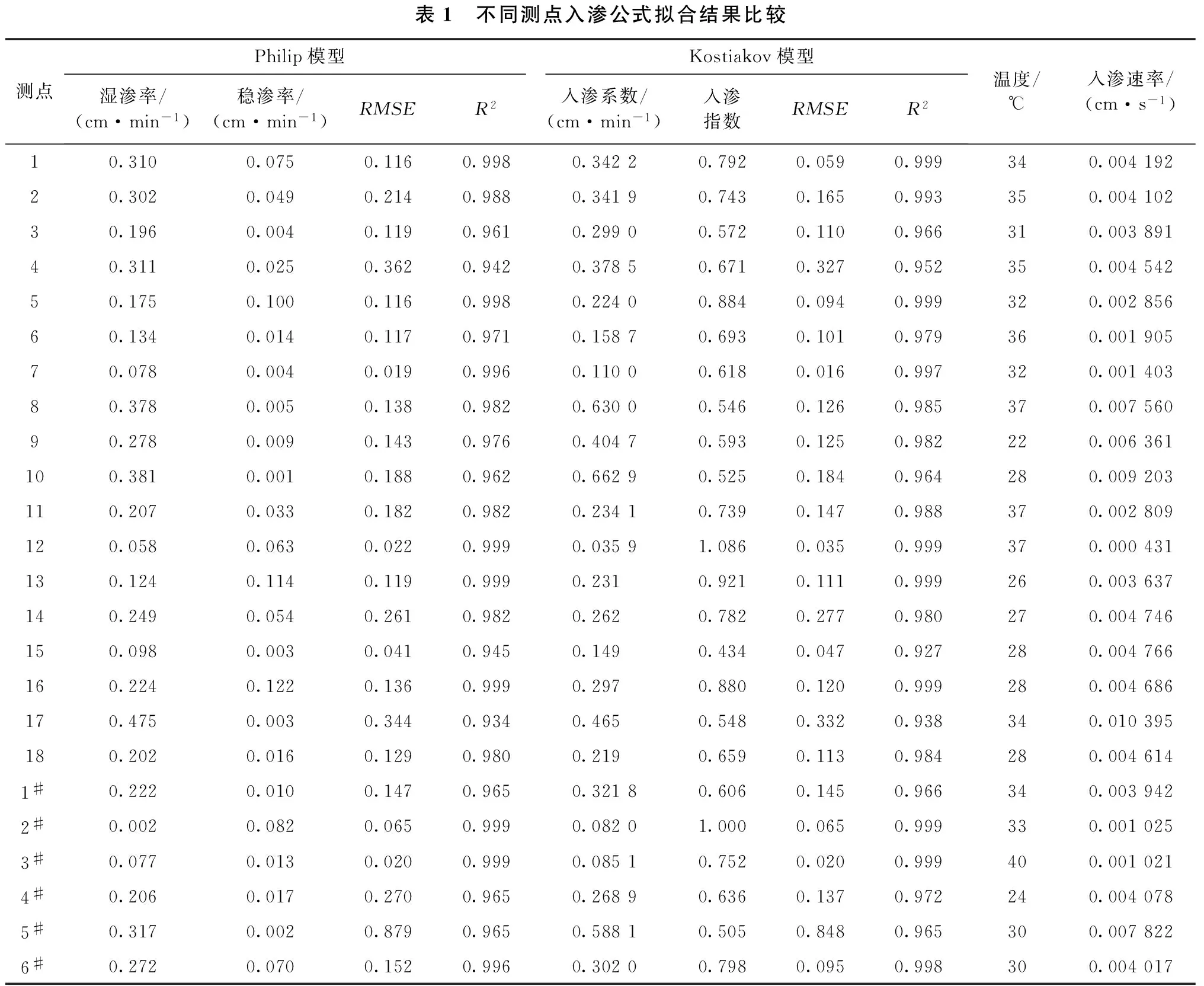
表1 不同测点入渗公式拟合结果比较测点Philip模型Kostiakov模型湿渗率/(cm·min-1)稳渗率/(cm·min-1)RMSER2入渗系数/(cm·min-1)入渗指数RMSER2温度/℃入渗速率/(cm·s-1)10.3100.0750.1160.9980.34220.7920.0590.999340.00419220.3020.0490.2140.9880.34190.7430.1650.993350.00410230.1960.0040.1190.9610.29900.5720.1100.966310.00389140.3110.0250.3620.9420.37850.6710.3270.952350.00454250.1750.1000.1160.9980.22400.8840.0940.999320.00285660.1340.0140.1170.9710.15870.6930.1010.979360.00190570.0780.0040.0190.9960.11000.6180.0160.997320.00140380.3780.0050.1380.9820.63000.5460.1260.985370.00756090.2780.0090.1430.9760.40470.5930.1250.982220.006361100.3810.0010.1880.9620.66290.5250.1840.964280.009203110.2070.0330.1820.9820.23410.7390.1470.988370.002809120.0580.0630.0220.9990.03591.0860.0350.999370.000431130.1240.1140.1190.9990.2310.9210.1110.999260.003637140.2490.0540.2610.9820.2620.7820.2770.980270.004746150.0980.0030.0410.9450.1490.4340.0470.927280.004766160.2240.1220.1360.9990.2970.8800.1200.999280.004686170.4750.0030.3440.9340.4650.5480.3320.938340.010395180.2020.0160.1290.9800.2190.6590.1130.984280.0046141#0.2220.0100.1470.9650.32180.6060.1450.966340.0039422#0.0020.0820.0650.9990.08201.0000.0650.999330.0010253#0.0770.0130.0200.9990.08510.7520.0200.999400.0010214#0.2060.0170.2700.9650.26890.6360.1370.972240.0040785#0.3170.0020.8790.9650.58810.5050.8480.965300.0078226#0.2720.0700.1520.9960.30200.7980.0950.998300.004017
2.2碎石土渗透特性不同方向的平均变异与二维平面各向变异比较
由表2可知碎石土饱和导水率在南北方向(斜坡长轴方向)、东西方向以及坡顶、坡腰、坡脚区域的空间变异性均属于中等变异性。坡顶与坡腰入渗率的空间变异性相对较大(变异系数分别为45%、77%)。碎石土水分空间分布在南北方向(斜坡长轴方向)、二维水平面和三维空间上表现为中等变异性,其变异系数分别为20%、29%、37%,而垂直方向变异系数为4%,属弱变异性(见表3)。这说明含水率在空间整体分布下变异系数相对较大,而在垂直方向水分分布的变异程度相

表2 各方向碎石土入渗率统计特征值类别样本数平均数标准差变异系数南北方向60.0042140.0011750.26东西方向30.0042140.0008760.19坡顶60.0054740.00244880.45坡腰60.0046280.00357360.77坡脚60.0035810.00100010.28

表3 各方向碎石土含水率统计特征值类别样本数平均数/%标准差/%变异系数南北方向612.522.450.20东西方向312.521.700.14垂直方向512.520.530.04二维方向1812.523.690.29三维方向9012.524.670.37
对较小。
由于以上研究中南北方向的长度远大于东西方向,为了合理比较南北和东西两方向的变异程度,可采用6 m×8 m的“移动窗”由坡顶向坡脚滑动,并计算每个“移动窗”内堆积碎石土入渗率与平均含水率在两个方向上的变异系数。由表4可知,坡顶与坡腰处入渗率变异系数表现为东西方向大于南北方向,而在坡脚处入渗率变异系数表现为东西方向小于南北方向。东西方向入渗率变异系数随着海拔的下降呈逐渐减小的趋势。堆积碎石土含水率东西方向的变异系数大于南北方向的变异系数,而碎石土含水率的变异系数随海拔变化的规律不明显(见表5)。

表4 不同区域堆积碎石土入渗率在二维平面东西方向和南北方向变异系数的比较滑动窗口南北方向变异系数东西方向变异系数10.36570.415620.16400.576030.14680.230940.34580.272450.28970.2066
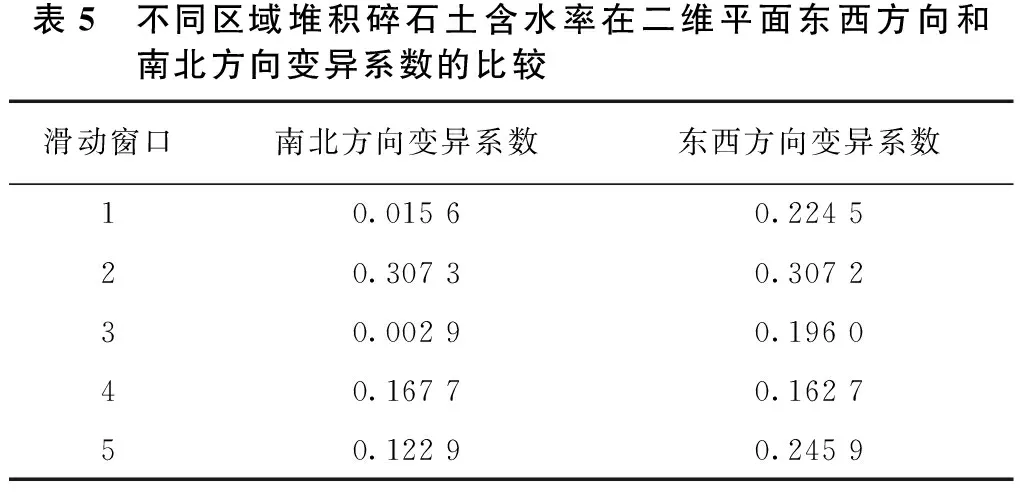
表5 不同区域堆积碎石土含水率在二维平面东西方向和南北方向变异系数的比较滑动窗口南北方向变异系数东西方向变异系数10.01560.224520.30730.307230.00290.196040.16770.162750.12290.2459
2.3碎石土渗透特性在各方向上的变化趋势
由于斜坡重力、搬运、剥蚀等地质作用,坡顶粒径大于60 mm碎石含量大,导致碎石土之间的空隙相对较大,而坡脚小粒径碎石(粒径2~10 mm)含量多,碎石之间的孔隙相对较小。由图3可见,沿坡长轴线方向从上到下,堆积碎石土入渗速率呈现出相对减小的趋势,即坡顶入渗速率>坡腰入渗速率>坡脚入渗速率。堆积碎石土水分在坡面的分布呈现坡脚、坡腰含水率相对较高(12%~15%)而坡顶含水率相对较少(9%~10%)的分布情况(见图4)。这是因为坡顶的地形坡度相对陡峭(29°~32°)而坡脚与坡腰的地形坡度相对平缓(22°~24°),在重力的作用下,雨水顺着斜坡方向发生了斜向迁移,雨水都聚积在坡腰与坡脚处,使得坡腰与坡脚的含水率比坡顶含水率要高。

图3 沿坡轴线方向碎石土入渗率分布图
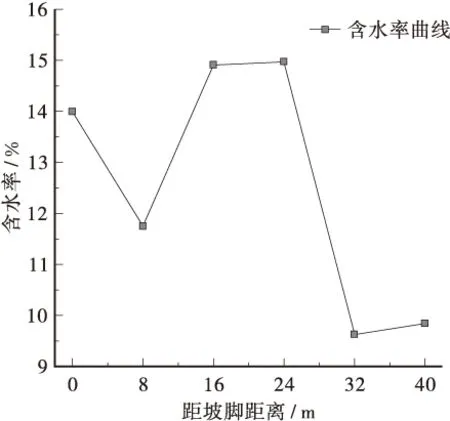
图4 沿坡轴线方向碎石土含水率分布图
通过现场试验可得(见图5),碎石土水分含量随土层深度的增加(0~25 cm)先增加至临界深度15 cm左右(含水率达13.27%)后又逐渐缓慢减少(含水率达11.77%)。在碎石土层之间,不仅碎石土含水率存在差别,且各层之间碎石土含水率的变异程度也不同。由表6可见,各层碎石土含水率变异系数值在31%~44%之间,属于中等变异,但是随着土层深度的增加,变异系数变化规律不明显。
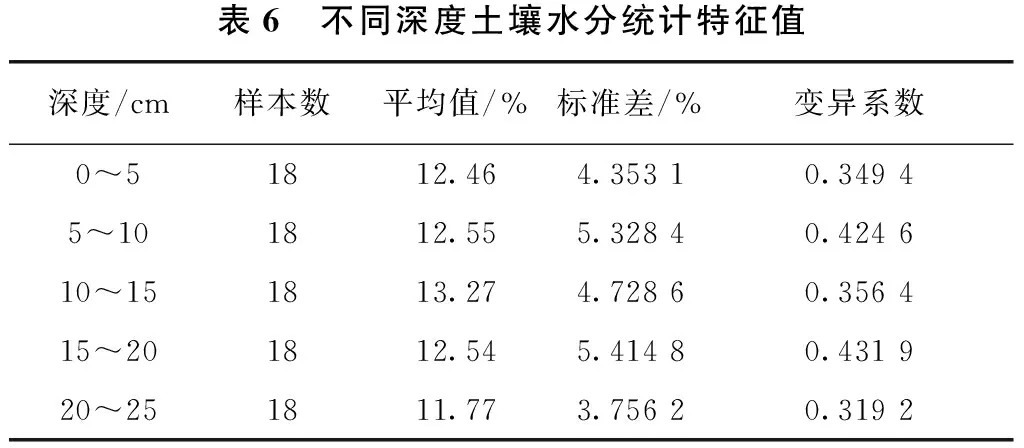
表6 不同深度土壤水分统计特征值深度/cm样本数平均值/%标准差/%变异系数0~51812.464.35310.34945~101812.555.32840.424610~151813.274.72860.356415~201812.545.41480.431920~251811.773.75620.3192

图5 含水率随深度变化分布图
3结论
1) 对于堆积碎石土而言,采用Kostiakov公式描述其入渗过程效果最好且具有普适性。
2) 饱和导水率在南北方向(斜坡长轴方向)、东西方向以及坡顶、坡腰、坡脚区域的空间变异性均属于中等变异性,且坡顶与坡腰入渗率的空间变异性相对较大。坡顶与坡腰处入渗率变异系数表现为东西方向大于南北方向,而在坡脚处则相反。东西方向入渗率变异系数随着海拔的下降呈逐渐减小的趋势。
3) 碎石土水分空间分布在南北方向(斜坡长轴方向)、二维水平面和三维空间上表现为中等变异性,其变异系数分别为20%、29%、37%,而垂直方向变异系数为4%,属弱变异性。
4) 沿坡长轴线方向从上到下,堆积碎石土入渗速率呈现出相对减小的趋势,即坡顶入渗速率>坡腰入渗速率>坡脚入渗速率。斜坡坡脚与坡腰的含水率相对较高(12%~15%)而坡顶含水率相对较少(9%~10%)。坡表平均含水率沿垂直方向随着地层深度增加先增加后减小,在距地表10~15 cm深度范围含水率最大。
参考文献:
[1] 贺可强,周敦云,王思敬.降雨型堆积层滑坡的加卸载响应比特征及其预测作用与意义[J].岩石力学与工程学报,2004,23(16):2665-2670.
[2] 许建聪,尚岳全,王建林.松散土质滑坡位移与降雨量的相关性研究[J].岩石力学与工程学报,2006,25(S1):2854-2860.
[3] 杨艳芬,王全九,曾辰,等.土石混合介质水分入渗特性试验研究[J].水土保持学报,2009,23(5):87-90.
[4] 董辉,罗潇,史超,等.气阻作用下堆积碎石土渗透规律[J],山地学报,2015,33(3):365-373.
[5] Wang Z,Feyen J,Nielsen D R,et al.Two-phase flow infiltration equations accounting for air entrapment effects[J].Water Resources Research,1997,33(12):2759-2767.
[6] 周中,傅鹤林,刘宝琛,等.土石混合体渗透性能的正交试验研究[J].岩土工程学报,2006,28(9):1134-1138.
[7] 许建聪,尚岳全.碎石土渗透特性对滑坡稳定性的影响[J].岩石力学与工程学报,2006,25(11):2264-2271.
[8] 冶运涛,伍靖伟,王兴奎.双套环测定土壤渗透系数数值模拟分析[J],灌溉排水学报,2007,26(3):14-18.
[9] SL345-2007,水利水电工程注水试验规程[S].
[10] SL237-1999,土工试验规程[S].
[11] Khanna,M.,Malano,H.M.Modelling of basin irrigation systems:A review[J].Agricultural Water Management,2006,83(1):87-99.
[12] Philip,J.R.The theory of infiltration:1.The infiltration equation and its solution[J].Soil Science,1957,83(5):345-358.
[13] Kostiakov,A.N.On the dynamics of the coefficient of water-percolation in soils and on the necessity for studying it from a dynamic point of view for purposes of amelioration[C].Moscow:Transcations Communication International Society Soil Science 6th,1932.
文章编号:1008-844X(2016)02-0018-05
收稿日期:2016-03-18
作者简介:李园园( 1980-) ,男,工程师,主要从事高速公路建设与管理工作。
中图分类号:U 416.1
文献标识码:A

