风力发电机温升故障预警方法研究

刘　轩, 孙建平

(华北电力大学 控制与计算机工程学院，河北保定071003)



风力发电机温升故障预警方法研究

刘轩, 孙建平

(华北电力大学 控制与计算机工程学院，河北保定071003)

摘要：针对传统PCA在解决变量重要性差异很大问题时的局限性，提出一种结合reliefF算法和加权主元算法的方法。该方法首先采集张家口某风场5月某段时间内风力发电机组运行数据并建立数据集，通过reliefF算法确定权值向量W，进而使用加权主成分分析法建立正常工作状态下发电机温度模型。利用该模型对同一机组另一段时间运行数据进行故障检测，通过对统计量HotellingT2(简称T2)和平方预测误差(简称SPE)的趋势分析最终确定机组运行状态。实验结果表明，提出的方法准确预测出了发电机的温升故障，并减少了误报情况。

关键词：加权主成分分析；发电机温度；reliefF算法；T2统计量；SPE统计量

0引言

近年来，我国风电事业发展迅速，伴随着风力发电机组种类和数量的不断增加风力发电机组在运行中产生了各种故障，严重影响设备运行效率。而发电机作为发电机组的重要部件之一，发电机系统的运行状态最直接影响着整个发电机组运行的性能和效率。所以，研究其故障诊断技术显得十分必要。本文以永磁同步电机为例，根据相关文献资料中所出现的故障情况统计和分析，归纳总结出永磁同步电机故障主要分为定子绕组故障、转子故障、温度升高故障等[1]。

1992年，Kira和Rendell通过文献[2]提出Relief算法，但该算法主要讨论两类问题分类情况。之后，为使Relief系列算法可以解决多类问题，Kononenko 在文献[3]中提出了ReliefF算法。Relief系列算法作为一种特征权重算法，不但有较高的运行效率，而且不限制数据类型。该算法根据与类别相关性的高低来赋予变量不同的权重，但该算法不能高效地去除原始变量间的冗余特征。主元分析(Principal Component Analysis，PCA)是一种多元统计方法，其利用原始数据变量之间的相关性，通过少数几个变量的线性组合来解释其他变量，从而实现降维的目的。主元分析可以很好地完成数据与图像的压缩，进而减少数据冗余并提取重要信息，广泛应用于人脸识别、故障检测等领域。针对传统的主元分析算法和ReliefF算法各自的局限性，本文提出了一种结合ReliefF算法的改进PCA算法。其基本思想是：通过ReliefF算法得到各变量特征权重，确定各变量权值W，进而采用加权主元分析法建立发电机温度与其影响因素之间的关系模型。通过HotellingT2和平方预测误差的计算来实现对风力发电机的状态监测和故障诊断。

1ReliefF算法

由于Relief算法的简单和高效性，使其应用广泛，但其局限性在于只能处理两类别数据。Kononenko在文献[4]中扩展了Relief算法，将分类视为一类对多类关系解决了多类问题，用来处理噪声数据和不完整数据。目前，ReliefF算法应用于人体行为识别研究[5]、无线电信号识别[6]和聚类研究分析[7]中。ReliefF算法输入为训练样本集合D，随机选择出的样本个数m，特征权重阈值，以及最邻近样本个数K；输出为各变量的特征权值向量。其中m也就是迭代次数，最大取值为样本集D的样本数。算法流程图为图1。

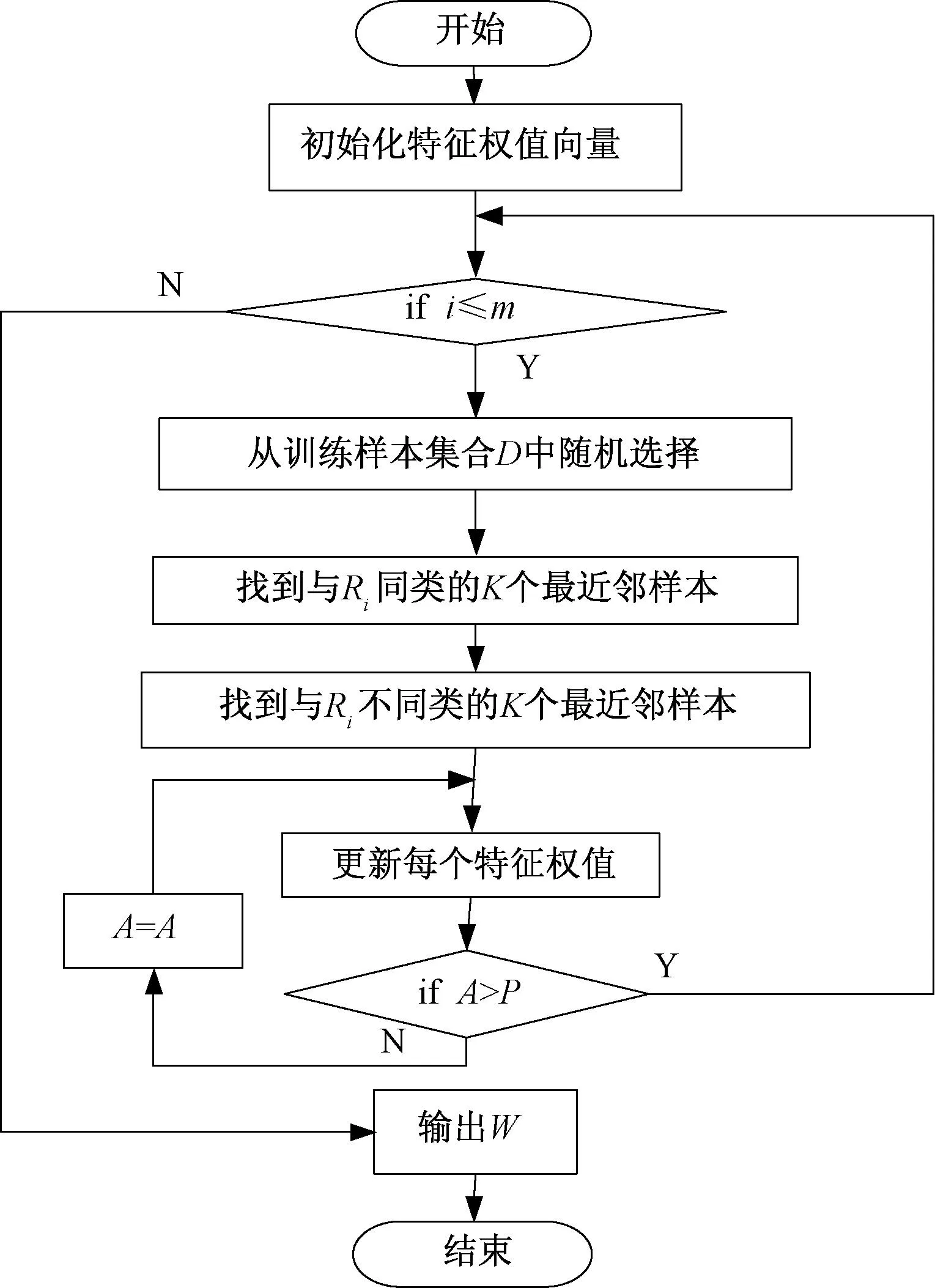
图1　reliefF算法流程图

其中特征权重计算公式：

(1)

式中：P(C)是C类目标样本数占样本总数的比例；Mj(C)表示第C类目标的第J个最邻近样本；diff(A,R1,R2)表示样本R1和R2在特征值A上的差，计算公式如下：

(2)

2加权主成分分析

主成分分析(PCA)作为一种多元统计方法，利用原始变量之间的相关性，使用原来变量的少数几个线性组合来表示原来变量，从而实现降维。主元分析可以很好地完成数据与图像的压缩来减少数据冗余并提取重要信息，广泛应用于人脸识别、故障检测等领域。由于传统的PCA算法没有考虑到样本间相互存在的重要度差异，往往不能有效地处理小样本问题中的离群点，不同物质的样本不能清晰的隔离分布。为此，许多加权 PCA(Weighted Principal Component Analysis,WPCA)算法相继而出[8-12]。

例如，文献[8]7中提出了一种基于PCA的样本加权特征提取算法，在Yale人脸库上的实验表明该方法具有很好的鲁棒性和识别率。文献[12]中指出，基于不同特征在识别过程中所起不同作用这种事实，采取加强关键点如眼睛、鼻子和嘴巴等部位来提高人脸识别率。

2.1算法步骤

在工业过程中，采集传感器信号列成数据矩阵Xn×m，其中n为样本个数，m为矩阵维数，代表传感器测点个数即变量个数。

加权主元的分析运算分为以下几个步骤：

(1) 对原始数据矩阵X进行标准化运算，对数据进行无量纲化和去除变量相关性处理，即：

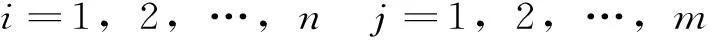
(3)

(2) 按照文献[4]中给出的加权函数方法计算权值向量W，表达式为：

(4)

(5)

(6)

(7)

式中：Λ为特征值构成的对角阵；V即所求的特征向量。

(4) 选取主元个数。本文采用方差贡献率法选择能概括数据主要变化的前Kp个主元，各主元累计贡献率：

(8)

累计贡献率选取过高，导致选取过多主元个数，造成数据冗余。而选取过低则会导致选取主元不能够充分代表原数据矩阵。一般情况下，选择累计贡献率达到 85%以上时候的Kp个主元代替原n个变量，这样建立的主元模型最能够代表原数据矩阵特征，又不会造成数据冗余。

(5) 建立主元模型：

(9)

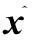
2.2统计指标

2.2.1 平方预测误差Q

(10)

Vkp为由V前kp列构成的特征向量矩阵。平方预测误差也称Q统计量，给定显著水平α时，Q统计指标的控制限Qα，其计算公式为：

(11)

在正常情况下，Q统计指标的值应处于控制限规定范围之内，故障情况下会超出控制限。

2.2.2 HotellingT2

(12)

式中：Λkp由前Kp个特征值组成的对角矩阵；T2统计指标的实质是向量X在主元空间投影向量单位正规化后的长度。T2统计量服从F分布(F(kp,n-kp))，n为样本点个数。给定显著性水平α时统计量的控制限，其计算公式为：

(13)

在正常情况下，T2统计量的值应该处于控制限范围内，故障发生后，统计量超出控制限。文献[14]指出，在实际工业过程中，T2和SPE统计量的4种检测结果。当T2未超限且SPE未超限时，系统运行正常；当T2超限且SPE未超限时，这种情况可能由系统的正常工况漂移引起，也可能是由于故障未显著改变变量之间的关系，有潜在故障可能；当T2未超限且SPE超限时，表明系统正常工况下变量间的相关结构被破坏，可能产生过程故障或传感器故障；当T2与SPE超限均超限时，说明系统运行异常，有故障发生。

3发电机温度预警模型

3.1发电机温度监测

发电机温度轴承温升是发电机考核的一个指标，文献[15]中指出轴承的温度信号在机组安全运行监控中有重要地位。发电机的温度过热往往是发电机故障的综合表现。导致发电机过热的因素有很多，冷却系统故障和定子长时间大电流运转都可能造成发电机急剧升温。本文选择建立基于温度变量的风力发电机故障预警模型，使用转子轴承温度值来表征发电机温度。本文选用的SCADA数据为张家口某风电场在2014年5月21日至23日期间，对某台风电机组正常工作时每10 min采集一次的SCADA数据，成为数据集1，其中转子轴承温度和其他相关变量的数据趋势如图2所示。通过对风电机组运行数据分析，在SCADA系统中发电机温度与其他多个变量存在关系。各变量与发电机温度之间有直接或间接的关系，各变量之间相互独立，也可能存在相关性。

图2　2014年5月21日至23日期间发电机温度及相关变量趋势图

由图2可知，风速在大多数情况下低于切出风速。在第297～348点之间风速超过切出风速，此时发电机组切出电网，停止发电，发电机温度稳步下降。在风速处于额定风速以上，切出风速以下时，机组并网功率和发电机转速恒定，发电机温度主要受环境温度及冷却风温影响。当风速处于切入风速以上，额定风速以下时，发电机温度主要受风速、机组并网功率、发电机转速影响。

3.2发电机温度建模仿真实验

根据2014年5月21日至23日期间风电机组的报警记录、停机记录，将数据集1中SCADA系统中机组故障停机时段、风速低于切入风速时段、风速高于切出风速时段的数据从建模数据中删除，得到机组正常状态下变量运行数据，记为Xn×m。另采集同一风机2014年5月26日至2014年5月28日期间风机运行数据(称为数据集2)进行检测和诊断。风机转子轴承温度和其他相关变量数据运行趋势为图3 所示。在2014年5月30日对风电机组进行计划停机检修。检修过程中发现发电机转子轴承链接处出现不同程度细小裂纹，这使得发电机转子绕组摩擦增大，产生多余热量导致发电机温度升高。如果在故障发生之前，不采取有效的故障预测方法预测故障发生，任其异常持续发展将导致机组故障停机。

图3　2014年5月26日至2014年5月28日期间发电机温度及相关变量趋势图

采用传统PCA对数据集Xn×m建模并求其主元，模型建立后，将数据集2作为检测数据，记录SPE和T2统计量。

通过观察统计量数据趋势，获取机组整体运行状态的实时信息。其中，SPE统计量反映某一时刻测量值相对于模型的偏离程度；T2统计量反映主元模型内部的各个向量模的大小变化来反映变量的变化情况；观察图4，T2统计量的阈值为13.771 1，发现从200采样点后主元空间中数据波动较大，但未超出阈值；对于SPE统计量，阈值为0.650 7，从200采样点后残差空间数据SPE统计量持续超出阈值，判定此时发电机温度值异常，机组存在出现故障的可能。而200采样点之前出现一些间断的误报点，说明使用传统主元分析的建模方法不完备，方法存在缺陷。

图4　PCA统计量监控图

传统PCA算法不仅可以消除样本间相互重叠的信息，而且能根据样本内各变量所提供的原始信息自动生成非人为的权系数，但它并未考虑不同样本在识别过程中互相存在的重要度差异[4]。所以，针对传统主元算法存在的缺陷，引入一个权值向量W，将每个变量赋以一定的权值从而突出其在整个数据集中的不同重要性，变量的权值代表其在总体中的相对重要性。

根据发电机转子轴承温度将数据集分为两类，正常温度范围类(类标签为“0”)和过高温度范围类(类标签为“1”)，使用ReliefF算法，分别计算m个相关变量与类的相关性权值，计算结果如表1所示。根据影响发电机温度的变量相关性权值，可以将影响发电机温度的变量按影响程度大小排序。各变量中影响风力发电机温度程度最高的是发电机转子轴承温度、环境温度，风速、并网功率、发电机转速对其影响次之，冷却风温对其影响相比较其他变量程度最小。本实验根据影响程度大小将权值系数矩阵W设定为W=[0.8∶1∶0.8∶1.2∶1.3∶1]。

表1　各相关变量与发电机温度相关性权值

将数据集2经过加权算法后再进行检测，记录SPE和T2统计量，检测结果为图5所示。T2统计量的阈值为11.701 2，从200采样点后主元空间中数据波动较大，但未超出阈值；对于SPE统计量，阈值为3.364 5，从200采样点后残差空间数据SPE统计量持续超出阈值，判定此时发电机温度值异常，机组存在出现故障的可能。比较图4与图5，可以看出，SPE统计量中多个误差点已经被消除，说明了结合reliefF算法的加权主成分分析法的有效性。

4结论

风力发电机组SCADA系统中记录的发电机运行数据可以较好地反映发电机运行状态。针对传统PCA在解决变量重要性差异较大问题时的局限性，本文提出一种结合reliefF算法和加权主元分析法的故障检测方法，首先根据风电机组实际运行数据，建立影响发电机温度的变量集；进而采用reliefF算法得到各变量对发电机温度的相关性权值，根据权值设定权值向量W，进行加权主成分分析；观察T2和SPE统计量大小，确定机组运行状态变化。实例分析表明，本文所提的检测方法既能够使得每个样本在整个样本组中凸显出不同的重要度，又能完成数据压缩去除数据冗余。但同时，该方法也具有一定的局限性。由于影响发电机温度的因素还有许多，本文只讨论算法确定的几个主要变量，忽略其他变量的影响，有待进一步研究。

参考文献:

[1]杨锡运，郭鹏，岳俊红，等. 风力发电机组故障诊断技术[M].北京:中国水利水电出版社,2015.

[2]KIRA K,RENDELL L. A practical approach to feature selection [C] //Proc 9th International Workshop on Machine Learning,1992:249-256.

[3]KONONENKO I. Estimation Attributes：Analysis and extensions of RELIEF [C] //European Conference on Machine Learning,Catania: Springer Verlag, 1994: 171-182.

[4]陈佩. 主成分分析法研究及其在特征提取中的应用 [D]. 西安：陕西师范大学,2014.

[5]张洁. 基于加速度传感器的人体运动行为识别研究[J].自动化与仪器仪表,2016(3):228-229,234.

[6]杜利敏,陈河山,徐扬,等. 基于ReliefF和聚类的特征选择方法及其在无线电信号识别中的应用[J].河南大学学报(自然科学版),2014(3):347-350.

[7]陈晓琳,姬波,叶阳东. 一种基于ReliefF特征加权的R-NIC算法[J]. 计算机工程,2015(4):161-165.

[8]杨开睿. 基于重建误差的样本加权特征提取算法研究[D].徐州：中国矿业大学,2014.

[9]GU Shanmao,LIU Yunlong,LIU Lijun,et al. Weighted principal component analysis applied to continuous stirred tank reactor system with time-varying[C]//中国自动化学会控制理论专业委员会.第三十四届中国控制会议论文集(D卷).中国自动化学会控制理论专业委员会,2015:5.

[10]刘志军,王林,齐咏生. PCA和LDA融合方法及其在故障诊断中的应用[C]//中国自动化学会过程控制专业委员会.第25届中国过程控制会议论文集.中国自动化学会过程控制专业委员会,2014.

[11]李云彤,黄山,徐海明. 基于改进PCA的人脸识别算法[J]. 微型机与应用,2015(17):43-45.

[12]白小曼. 改进的加权主成分分析算法实现人脸识别[D].北京：北京交通大学,2006.

[13]李想. 基于主元分析的工业过程故障诊断算法研究[D].沈阳：沈阳大学,2010.

[14]王婉. 基于PCA的空调水系统的传感器故障检测与诊断研究[D].长沙：湖南大学,2014.

[15]霍娟,唐贵基,刘大宾,等. 基于温度信号的风电机组发电机实时可靠性监测新方法[J]. 可再生能源,2016(3):408-412.

Study on the Method of Wind Turbine Temperature Fault Warning

LIU Xuan，SUN Jianping

(School of Control and Computer Engineering, North China Electric Power University, Baoding 071003, China)

Abstract：Aimed at the limitations of the traditional PCA in solving the problem of variable big difference importance, this paper proposes a method comprising of reliefF Algorithm and Weighted Principal Component Analysis(WPCA).This method first collects the data of wind turbine operation in a certain wind farm in Zhangjiakou in May and sets up the data set，through the reliefF algorithm to determine the weight vector W, and uses the weighted principal component analysis method to establish the normal working state of the generator temperature model.The model is used to detect the faults of the same set of another period of time,and trend analysis of the model statistics HotellingT2(T2) and squared prediction error (SPE) to finalize the running status of the unit.The experimental results show that the proposed method accurately predicts the failure of the generator temperature rise, and reduces the false alarm situation.

Keywords：WPCA； generator temperature； reliefFalgorithm;T2statistics；SPE statistics

收稿日期：2016-04-18。

基金项目：河北省自然科学基金(F2014502059)。

作者简介：刘轩(1992-)，女，硕士研究生，主要从事风力发电机组故障检测方面的研究，E-mail：381192438@qq.com。

中图分类号:TM614

文献标识码:A

DOI:10.3969/j.issn.1672-0792.2016.06.007