一道中考选择压轴题的探究与思考*

☉山东省东营市胜利第六中学　于　彬☉山东省东营市胜利第十三中学　刘锦海



一道中考选择压轴题的探究与思考*

☉山东省东营市胜利第六中学于彬
☉山东省东营市胜利第十三中学刘锦海

在各省市的中考试题中选择题大都占据着一定的份量，再加上部分学生，甚至是部分老师对选择题不重视，因此有时选择题的得分往往影响着中考的成败.选择题，“麻雀虽小，五脏俱全”，特别是选择题的压轴题更是值得一线教师去研究，去品味，下面笔者以2015年滨州市中考数学试题第12题的探究过程为例进行简单介绍，欢迎批评和指正.

一、原题呈现

题目如图1，在x轴的上方，∠BOA（直角）绕原点O按顺时针方向旋转.若∠BOA的两边分别与函数的图像交于B、A两点，则∠OAB大小的变化趋势为（）.

图1

A.逐渐变小B.逐渐变大

C.时大时小D.保持不变

对于大多数考生而言，看到上述试题后，基本没有思路，不知如何下手.当然，由于此题是选择题，有一部分学生最后可能直接猜了一个答案，而笔者认为学生猜“保持不变”的可能性还是很大的，这应该与老师日常灌输的“考试技巧”有很大的关系，因此就这个角度来看，这道选择题的信度和效度就都大打折扣了，应该引起命题人的足够重视.不过，就这道题对学生的思维角度、考查角度及命题人的命制角度来看，还是值得“点赞”的一道中考试题.

二、解法探究

解法1：如图2，过点A、B分别向x轴作垂线，垂足分别为C、D.

图2

因为∠AOC +∠BOD = 90°，∠OBD+∠BOD=90°，所以∠AOC=∠OBD.

又因为∠ACO=∠ODB= 90°，所以△AOC∽△OBD.

根据反比例函数中k的几何意义知：S△AOC=1，S△OBD=，所以

解法2：如图2，过点A、B分别向x轴作垂线，垂足分别为C、D.

设AO=m，BO=n，∠AOC=α，由解法1可得∠OBD=α.

在Rt△AOC中，AC=msinα，OC=mcosα；

在Rt△BOD中，OD=nsinα，BD=ncosα.

于是，A点坐标为（mcosα，msinα），B点坐标为（-nsinα，ncosα），将上述两点分别代入和，得①②.

解法1与解法2相比，解法1显得更加巧妙一些，冒昧揣测一下的话也应该更加符合命题人的命题意图，此法综合运用了相似三角形、相似三角形的性质及反比例函数中k的几何意义等基础知识，注重了对核心知识的考查；当然，解法2中没有注意到反比例函数中k的几何意义，而是采用将点的坐标代入解析式，然后进行化简的方法，此法化简过程中具有一定的技巧性，同时也具有进入高中以后“解析几何”的味道，可以说达到了与解法1“殊途同归”的效果.

三、几点思考

1.提取关键词语

笔者根据多年的解题教学有一点体会，那就是部分题目的题干中有时会有一些暗示性的短语（称为关键词语），提示解题的方向或方法.比如，上述试题中的“变化趋势”就是解决该问题的关键词语.看到“变化趋势”，应该比较容易和函数进行关联，但是上述试题问的是“角度”的变化趋势，这应该增加了一定的难度，换言之，如果上述试题问的是“长度或面积”的变化趋势，学生可能更加容易和函数进行关联.总而言之，“变化趋势”应该起到了一定的提示作用，再结合题目中直角三角形的存在，顺势想到三角函数应该还是比较自然的.

2.识别基本图形

无论是解法1，还是解法2，都添加了相同的辅助线，构造了“一线三直角”这一相似的基本图形，可以说是这一基本图形为上述试题的后续求解指明了继续前进的方向.作为一线教师应该在教学中善于引导学生进行相应基本图形的积累和识别，只有这样，学生才能够在一些复杂的图形中识别出基本图形，进而顺利解决相关问题.此外，教师还应该注意一些基本图形的变式（比如“一线三直角”的变式图形），真正使学生能够做到“举一反三、触类旁通”，进而提高学生的解题效率.

3.抓住核心考点

中考试题是命题人集体智慧的结晶，往往注重对核心考点的考查.在中考的备考复习中，教师应该引导学生结合本地区往年的中考试题进行核心考点的总结，比如上述试题综合考查了相似三角形的判定、相似三角形性质的灵活运用及反比例函数中k的几何意义，可以说以上考点在每年的中考试题中都会出现，是高频考点，是核心知识，是整个初中阶段的主干知识，也是进入高中以后学习其他知识的基础所在，应该引起一线教师和学生的足够重视，在有限的中考复习时间里，取得最大的效益，起到事半功倍的教学效果和学习效果.

四、变式引申

下面结合上述试题和思考，给出该问题的一个变式，一个引申，以期可以引发读者更广泛的关注.

图3

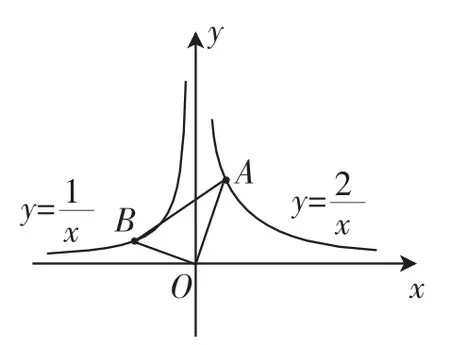
图4

五、结束语

解题能力应该是一线教师必须具备的基本能力之一，而解题教学则在单纯解题的基础上对一线教师提出了更高的要求，比如需要关注方法是如何获得的？考查了哪些考点？有无其他解法？哪种解法更简洁、易想？有无变式和引申？除此之外，更要关注学生的实际情况等，在此基础上才可能更好地开展解题教学，真正做到“入宝山而不空返”（罗增儒语），在提高学生的同时，提高自己，做到教学相长.H

*本文系东营市教育科学十二五规划课题《“反思性课堂教学模式”下中学作业改革的研究与实践》（编号：125DYJG195）和《“导学·反思”和谐高效课堂教学的实践与研究》（编号：125DYJG210）的阶段性研究成果。