纤维力学性能对自捻纱线自捻程度的影响
崔 红 , 高秀丽 , 林洪芹 , 高大伟, 吕立斌
(1. 盐城工学院 纺织服装学院, 江苏 盐城 224000; 2. 河南工程学院, 纺织学院, 河南 郑州 450007)
纤维力学性能对自捻纱线自捻程度的影响
崔 红1, 高秀丽2, 林洪芹1, 高大伟1, 吕立斌1
(1. 盐城工学院 纺织服装学院, 江苏 盐城 224000; 2. 河南工程学院, 纺织学院, 河南 郑州 450007)
为研究纤维力学性能对自捻纱线自捻程度的影响,根据自捻形成过程的总应变能守恒推导出自捻捻回角和纤维抗弯刚度、扭转刚度的关系。结果分析表明:纤维抗弯刚度越大,自捻纱线的自捻捻回角越小;纤维扭转刚度越大,则自捻纱线的自捻捻回角越大;自捻捻回角的大小和纤维的扭转刚度和抗弯刚度之比成正比,即随着纤维扭转刚度和抗弯刚度之比的增大,自捻捻回角增大,所加自捻捻回数增多。通过对苎麻、涤纶、腈纶、羊毛4种纤维所纺的自捻纱线的半周期捻回数进行测试,验证了上述关系并得出结论:羊毛和腈纶纺纱时所得自捻捻回数较多,较适合采用自捻纺纱方式进行纺纱;而涤纶和苎麻所加自捻捻回数较少,不太适合采用自捻纺纱方式开发纺织品。
自捻; 总应变能; 捻回角; 抗弯刚度; 扭转刚度
自捻纺纱是一种新型纺纱形式[1-2],自捻纱线的特点是存在3种纱段:有捻-有捻纱段,有捻-无捻纱段和无捻-无捻纱段[3-4],其中有捻-有捻纱段形成纱线的强捻区,有捻-无捻纱段和无捻-无捻纱段形成纱线的弱捻区。自捻纱线就是由强捻区或弱捻区交替周期性出现,在纱线上形成一段S捻一段Z捻其间间隔弱捻区的纱线结构。自捻纱线的捻度是衡量自捻纱线结构的一个重要指标,早在20世纪70年代Walls[5]就推导出了自捻捻度分布函数的公式,在此基础上,由于自捻纺纱从自捻罗拉至汇合钩汇合方式经过了无数次的演变,故几种不同汇合方式的捻度分布函数、不同汇合方式的捻度分布以及通过2种不同捻度分布函数计算方法所得到的自捻纱线的捻度等内容得到了研究并取得了一定的结果[4,6]。自捻捻度分布函数公式中建立了自捻捻度和纱线周长、自捻罗拉往复运动动程、前罗拉钳口与自捻罗拉钳口线距离以及自捻罗拉钳口与汇合钩之间的距离等之间的数量关系,但是没有具体反映出自捻捻度与原料性能之间的关系。纺纱方法决定纱线结构,而纱线结构本身又由原料的性能和加捻方式所决定[7-8]。自捻纺纱的成纱原理是由一对往复运动的自捻罗拉在纱线输出的同时对2根纱线同时进行搓捻,纤维条在获得捻度的同时在2根纤维条内部积聚了弯曲应变能和扭转应变能,还包括由于纤维条张力产生的拉伸应变能,当2根纤维条在汇合钩处汇合,并且2根纤维条存在周向约束时,储存在2根纤维条中的应变能开始释放,转变成自捻纱线的拉伸应变能、弯曲应变能和扭转应变能,在成纱前后,根据能量守恒定理,总应变能保持不变[9-10],所以自捻形成的过程和纤维原料本身的力学性能如弯曲和扭转是息息相关的。
纤维原料不同,原料本身的扭转刚度和抗弯刚度不同,所形成的自捻捻度大小不同,最终会造成自捻纱线断裂强度的差异,为此,本文研究了原料的力学性能包括扭转刚度和抗弯刚度对自捻捻度的影响,对研究不同纤维原料是否适合自捻纺纱,对产品开发具有非常重要的意义。
1 原料性能和实验安排
纤维原料选用羊毛、涤纶、腈纶和苎麻。其基本性能如长度、线密度和断裂强度如表1所示。

表1 纤维原料性能指标Tab. 1 Fiber properties
将上述4种不同的纤维原料采用相同的自捻纺纱工艺纺制50 tex自捻纱线。通过测试自捻纱线半周期长度上的捻回数得到不同纤维原料自捻程度的大小。自捻纱线半周期长度上的捻回数采用直接退捻法在Y331A型纱线捻度仪上进行测试。每种纱线的捻回数取10组数据的平均值。
2 自捻程度分析
自捻程度指的是纱条受到搓捻后发生自捻的程度,用自捻的捻回角(Q)表示,捻回角越大,说明自捻程度越高,自捻捻回数越多;反之,捻回角越小,自捻程度越低,自捻捻回数越少。
由于自捻过程遵循能量守恒定律,纱条先经过搓捻后发生自捻,在搓捻的过程中,会发生纱条的拉伸、弯曲和扭转,相应的能量如拉伸应变能、弯曲应变能和剪切应变能(扭转产生)构成总应变能积聚在自捻纱条中,积聚的能量会促使自捻发生,自捻完成后,总应变能不变,并达到最小值。
如果将自捻纱条中的1根纤维视为等直圆杆,等直圆杆的拉伸、弯曲和扭转会使纤维产生变形。
纤维由于扭转产生的剪切应变能Sj可表示为
(1)
式中:G为纤维的剪切模量;Ip为纤维截面极惯性矩;L为纤维的长度;φsp为扭转角度。
又φsp=2πTsp
(2)
式中Tsp为自捻股线中的纱条捻度。
将式(2)代入式(1)得
(3)
纤维由于拉伸产生的拉伸应变能Sl可表示为
(4)
式中:FN为拉伸应力;E为纤维模量;A为纤维截面积。
又FN=Eεsp
(5)
式中εsp为纱条中的纤维伸长。
εsp=secQ-1
(6)
将式(5)、(6)代入式(4)得
(7)
式中R为纤维横截面的半径。
纤维由于弯曲产生的弯曲应变能Sw可表示为
(8)
式中:I为纤维截面惯性矩;K为纤维弯曲曲率。

(9)
式中Rp为自捻纱线的半径。
将式(9)代入式(8)得
(10)
纤维扭转、拉伸、弯曲所产生的总应变能(Sfz)为上述3种应变能之和。
Sfz=Sj+Sl+Sw=
(11)
(12)
将式(12)代入式(11)得
(13)
纱条长度L0时,纱条中纤维总根数M为
(14)
式中:V0为纱条长度L0时纱条体积;Vf为纤维体积;rf为纤维半径;lf为纤维长度。
由于纤维扭转、拉伸、弯曲集聚能量形成自捻纱的总应变能SZ为
(15)
当自捻完成时,自捻纱的总应变能达到最小值,此时,求自捻纱的总应变能相对于捻回角的导数,排除cosQ=1,Q=0的情况,得到:
(16)
3 纤维力学性能对自捻程度的影响
3.1纤维的抗弯刚度
纤维在受到外力作用时抵御纤维形状进行弯曲的能力叫做纤维抗弯刚度Rf[7]。纤维抗弯刚度Rf由公式表示为
1)微机继电保护装置具有4相电压3相电流输出的功能特点,能够方便进行各种组合输出,进行各种类型保护试验;
Rf=EI
(17)
如果将纤维抗弯刚度换算成与1tex相同线密度时的抗弯刚度,叫做纤维相对抗弯刚度Rfr。
(18)
式中:ηf为纤维弯曲时的截面形状系数,且ηf<1;ρ为纤维密度。
4种纤维的相对抗弯刚度如表2所示。由表可知,苎麻纤维、涤纶、腈纶、羊毛纤维的相对抗弯刚度按照从大到小的顺序表示为:苎麻>涤纶>腈纶>羊毛。
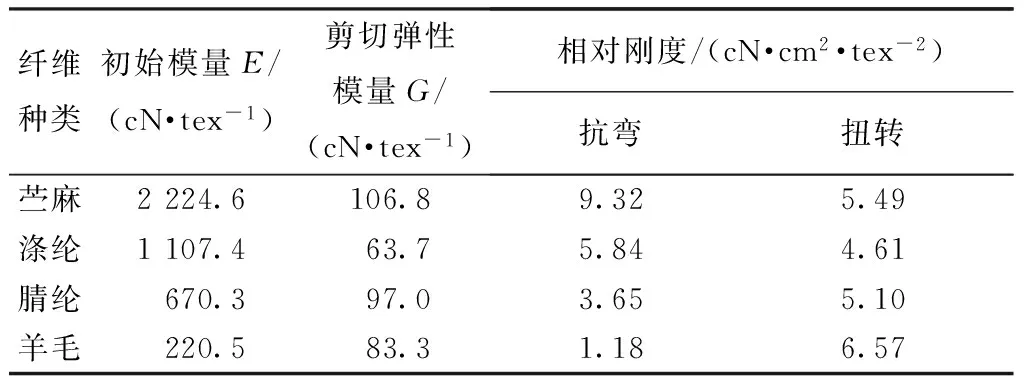
表2 纤维原料的力学性能Tab. 2 Fibers′ mechanical properties
3.2 纤维的扭转刚度
纤维在受到外力作用时抵御纤维形状进行扭转的能力叫做纤维扭转刚度Rt[7]。纤维扭转刚度Rt由式(19)表示为
Rt=GIp
(19)
如果将纤维扭转刚度换算成相同线密度如1tex时的扭转刚度,叫做纤维相对扭转刚度Rtr。
(20)
式中ηt为纤维扭转时的截面形状系数。
4种纤维的相对扭转性能见表2。由表可知,苎麻纤维、涤纶、腈纶、羊毛纤维的相对扭转刚度按照从大到小的顺序表示为羊毛>苎麻>腈纶>涤纶。3.3 自捻程度与纤维力学性能的关系
由式(16)得:
(21)
由式(21)可明显看出,表示自捻程度的捻回角Q与纤维的力学性能包括抗弯刚度Rf和扭转刚度Rt的关系。捻回角Q随着纤维扭转刚度Rt的增大而增大,随着纤维抗弯刚度Rf的增大而减小。从而进一步可得到,纤维扭转刚度Rt和抗弯刚度Rf之间的比值与表示自捻程度的捻回角Q成正比。分别计算苎麻纤维、羊毛、涤纶、腈纶扭转刚度Rt和抗弯刚度Rf之比,再分别纺制50 tex苎麻、羊毛、涤纶、腈纶的纯纺自捻纱线,并测量各自捻纱线半周期长度上自捻捻回数,得到上述4种不同纤维原料扭转刚度Rt和抗弯刚度Rf的比值与半周期长度110 mm上的捻回数对应值之间的关系,结果如表3所示。4种不同纤维原料扭转刚度Rt和抗弯刚度Rf的比值按照从大到小的顺序依次为:羊毛>腈纶>涤纶>苎麻。通过测试半周期长度上的捻回数大小,自捻捻回数从大到小的顺序为羊毛、腈纶、涤纶、苎麻,与理论分析结果一致。由此可见,涤纶和苎麻由于所加自捻捻回数较少,考虑到成纱强力等问题,一般不考虑采用自捻纺纱这种型式开发纺织品。而羊毛和腈纶更加适合采用自捻纺纱型式。

表3 自捻纱线半周期捻回数与力学性能的关系Tab. 3 Relationship between twist number on half cycle length and fiber mechanical properties
4 结 论
运用自捻纺纱过程的应变能守恒定理,推导出自捻捻回角Q与纤维力学性能之间关系的计算公式。公式表明自捻纱线的自捻程度(捻回角Q的大小)与纤维的抗弯刚度Rf和扭转刚度Rt有关,纤维的抗弯刚度Rf越大,纱线的自捻捻回角越小;纤维的扭转刚度Rt越大,纱线的自捻捻回角越大。自捻捻回角Q的大小和纤维的扭转刚度Rt和抗弯刚度Rf之比成正比,即随着纤维的扭转刚度Rt和抗弯刚度Rf之比的增大,自捻捻回角增大,自捻纱线的半周期捻回数越多。通过对苎麻、涤纶、腈纶、羊毛4种纤维纺制50 tex自捻纱线测试其半周期长度上的捻回数发现,羊毛的扭转刚度Rt和抗弯刚度Rf的比值最大,所纺自捻纱线半周期捻回数最多,苎麻的扭转刚度Rt和抗弯刚度Rf的比值最小,所纺自捻纱线半周期捻回数最少。羊毛和腈纶较适合采用自捻纺纱方式纺纱,而涤纶和苎麻则不太适合采用自捻纺纱方式进行纺织品开发。
FZXB
[1] 刘国涛, 谢春萍, 徐伯俊. 新型纺纱[M]. 北京:中国纺织出版社, 1999:131-142. LIU Guotao, XIE Chunping, XU Bojun. New spinning [M]. Beijing: China Textile & Apparel Press, 1999:131-142.
[2] 狄剑锋. 新型纺纱产品开发[M].北京:中国纺织出版社, 1998:4-8. DI Jianfeng. New Spinning Product Development [M]. Beijing: China Textile & Apparel Press, 1998: 4-8.
[3] 崔红, 肖志永, 郁崇文. 自捻纱的捻度分布特征分析[J]. 纺织学报, 2012,33(8):40-45. CUI Hong, XIAO Zhiyong, YU Chongwen. Analysis of twist distribution characteristic of self-twist yarn [J]. Journal of Textile Research, 2012,33(8):40-45.
[4] 崔红. 自捻纺纱纱线结构及其力学性能研究[D].上海:东华大学,2012:27-29. CUI Hong. Study on the mechanism structure and mechanical property of self-twist yarn[D]. Shanghai: Donghua University, 2012:27-29.
[5] WALLS G W. Oscillating rollers for self-twist spinning[J]. Journal of the Textile Institute, 1970, 61(6): 245-259.
[6] CUI Hong, YU Chongwen. Study of self-twist distribution functions in different convergence Modes[J]. Fibres & Textiles in Eastern Europe, 2012, 5(94): 26-29.
[7] 于伟东, 储才元. 纺织物理[M]. 上海:东华大学出版社, 2002:126-130. YU Weidong, CHU Caiyuan. Textile Physics[M]. Shanghai: Donghua University Press, 2002:126-130. [8] 姚穆. 纺织材料学[M]. 北京:纺织工业出版社, 1997: 401-417. YAO Mu. Textile Materials[M]. Beijing: Textile Industry Press,1997:401-417.
[9] TAYEBI A, BACKER S. The mechanics of self-plying structures: part I: monofilament strand[J].Journal of the Textile Institute, 1973, 64(12):704-710.
[10] HEARLE J W S. Structural mechanics of torque-stretch yarns: the mechanism of snarl formation[J].Journal of the Textile Institute, 1966, 57(10): 441-460.
Effect of fiber mechanical properties on twisting degreeof self-twist yarn
CUI Hong1, GAO Xiuli2, LIN Hongqin1, GAO Dawei1, LÜ Libin1
(1. College of Textiles and Clothing, Yancheng Institute of Technology, Yancheng, Jiangsu 224000, China;2. College of Textiles, Henan University of Engineering, Zhengzhou, Henan 450007, China)
In order to study the effect of fiber mechanical properties on twisting degree of self twist yarn, and the relationship formula between the twist angle and fiber bending stiffness, torsional stiffness is derived from the conservation of total strain energy during the process of self-twist spinning. The formula shows that the larger bending stiffness has the smaller twist angle and the bigger torsional stiffness has the larger twist angle. So the size of the twist angle is proportional to the radio of fiber torsional stiffness and bending stiffness, namely with the ratio of fiber torsional stiffness and bending stiffness raises, twist angle increases, and the number of the self-twist twists is greater. By testing the number of the self-twist yarn twists respectively spun from ramie, polyester, acrylic and wool, the above relationship is verified and the conclusion can be drawn as: wool and acrylic are more suitable for self-twist yarn by self-twist spinning with greater self-twists number, but polyester and ramie are not suitable for textile development by self-twist spinning with smaller self-twists number.
self-twist; total strain energy; twist angle; bending stiffness; torsional stiffness
10.13475/j.fzxb.20150201804
2015-02-09
2016-03-02
江苏省高校自然科学基金面上项目(15KJB430032);盐城市2014年度农业科技指导性计划项目(YKN2014017);盐城工学院人才引进项目(KJC2014012)
崔红(1972—),女,高级工程师,博士。主要研究方向为纺纱原理及应用。E-mail:cuih72@163.com。
TS 134.7
A

