基于协同理论的徐州地区区域经济可持续发展研究
单小珂 蔺莉


摘要:协同论以系统论、信息论、控制论、突变论等为基础,采用统计学和动力学相结合的方法,描述了各种系统和现象中从无序到有序转变的共同规律。以协同论为基本方法,对区域经济协同发展程度进行数据挖掘和客观评价,将有助于正确认识经济现象,为科学发展提供决策依据。本文对徐州区域经济发展进行了实证分析,对不同子系统指标间的相关系数进行计算,分析统计学显著效应,建立了相关系数矩阵,并进行了因子分析。在最小二乘法基础上,拟定了预测方程。研究结果表明,目前徐州经济发展仍以投资拉动为主,整体协同发展程度呈上升趋势,部分经济数据已具备显著自相关性特点。
关键词:徐州区域经济;协同度;相关性分析;可持续发展;研究
中图分类号:F207 文献识别码:A 文章编号:1001-828X(2016)012-000-03
一、 理论背景
一直以来,徐州是著名的重工业基地。规模经济不断扩大,在社会经济生活中起到的主导作用也越来越显著。近年来,以淮海经济圈为代表的徐州经济发展模式正在逐渐的形成规模效应,徐州城市的发展呈现出5个新变化:一是城市发展开始从外延式扩张向内涵式发展转变;二是城市软实力成为城市发展的核心竞争力;三是城乡统筹和城乡一体化成为城市发展的新格局;四是综合配套改革试验区的示范意义进一步凸显;五是城市群对城市建设与发展的作用日益显著。在这种大背景下,对徐州综合经济实力进行研究,不仅是对促进徐州本身又快又好的发展,还对于充分发挥,徐州社会经济,生活的主导作用都有着极其重要的意义。
本研究的目的如下:通过对描述徐州城市综合经济实力发展的各种指标进行协同度分析,一方面找出用来衡量徐州城市经济实力的各个指标之间的内在联系,另一方面,通过对样本数据和输出值的观察和拟合,利用多项式逼近,探索徐州经济发展的方程,以便对未来徐州经济的发展作出预测。
二、相关研究
德国物理学家哈肯20世纪70年代创立了协同学,哈肯认为系统内部不同子系统之间存在非线性的相互作用,从而形成协同关系,协同关系的本质是完成了混沌到有序、有序到混沌的改变。贝塔朗菲(1945)首次阐明了系统论的基本思想,贝塔朗菲认为系统论是以一般系统为研究对象,广泛采用数学建模的方法,量化研究并描述系统功能。
国内对区域经济协同发展的研究仍处在起步阶段,现有研究在研究框架与内容上基本相同,而在具体研究方法上略有不同。从研究内容上来看,现有研究基本集中在对政府公布的经济运行指标及其数据进行量化计算和相关性分析,从中找出不同指标之间的相互关系,例如杨洁(2009)、孙君俐(2010)等人的研究。在具体研究方法上,各有不同:例如,Ke(2008)等人利用层次分析法和加权指标法,分析研究区域经济协同发展的状况,汤玲等人提出了基于距离协调度模型的研究思路,郑广华(2010)等人通过引入离差系数模型,利用灰色关联模型测量了系统现有状态,与理想状态之间的差距,从而达到衡量系统发展协同度的目的,师帅(2014)等人利用BP的系神经网络和SOV网络偏重对历史样本数据的曲线拟合,以及在此基础上实现经济发展模式自动分类的目的。本文从相关性分析入手,对现有指标提取公因子,借助最小二乘法拟定发展方程,并引入数据自相关分析,从而消除数据序列的非平稳性特征。
三、区域发展系统及其评价模型构建
1.区域发展系统构成
区域发展系统从结构及功能上可将其划分为四个子系统: 社会子系统、经济子系统、环境子系统、资源子系统,彼此相互作用、相互影响。可持续发展是在4个子系统之间寻找均衡态,通过对反映经济运行情况的各种指标的量化研究,找到彼此间的协同关系,通过规划求解找到最优通过规划求解找到最优临界点。
2.理论构成
协同理论研究的本质是通过对不同指标之间的欧几里德距离的量化计算, 反映系统显示状态理想状态的差距。首先对不同指标下采集的数据进行无量纲化处理; 其次对不同指标进行统计量分析, 包括频率的正态分布情况、卡方、游程、K-S分析;第三,对不同子系统指标间的相关系数进行计算,分析统计学显著效应,形成相关系数矩阵;第四,对系数矩阵进行样本因子分析,包括降维、公因子提取。第五,利用最小二乘法拟定方程,估算参数,评估观测值与计算值之间的残差。
(1)指标归一化
归一化是一种无量纲处理手段,使数值的绝对值变成某种相对值关系。在统计学中,归一化的具体作用是归纳统一样本的统计分布性。归一化在0-1之间是统计的概率分布,归一化在-1--+1之间是统计的坐标分布。常用的归一化方法有:
A Min-Max标准化
Min-Max标准化方法是对原始数据进行线性变换。设MinA和MaxA分别为属性A的最小值和最大值,将A的一个原始值x通过Min-Max标准化映射成在区间[0,1]中的值x',其公式为:
这种方法基于原始数据的均值(Mean)和标准差(Standard Deviation)进行数据的标准化。将A的原始值x使用z-score标准化到x'。z-score标准化方法适用于属性A的最大值和最小值未知的情况,或有超出取值范围的离群数据的情况。
(2)游程及K-S分析
A 游程检验
游程检验亦称连贯检验或串检验,是一种随机性检验方法,应用范围很广。取一个序列里的游程总数作为检验统计量,记为R。 设样本总数为N:
(3)相关度计算
Pearson相关系数用来衡量两个数据集合是否在一条线上面,它用来衡量定距变量间的线性关系。当两个变量都是正态连续变量,而且两者之间呈线性关系时,表现这两个变量之间相关程度用积差相关系数:
取值范围为[-1,1],r>0表示正相关,r<0表示负相关,|r|表示了变量之间相关程度的高低。特殊地,r=1称为完全正相关,r=-1称为完全负相关,r=0称为不相关。通常|r|大于0.8时,认为两个变量有很强的线性相关性。
偏相关分析是在控制其他变量的线性影响的条件下分析两变量之间的线性相关。控制变量为1时,称作一阶偏相关系数;控制变量为2时,称为二阶偏相关。控制变量为0时,称为零阶偏相关,也就是相关系数。计算公式:
偏相关系数的显著性检验步骤:提出零假设H0,即两总体的偏相关系数与零无显著性差异;选择检验统计量,其中r为偏相关系数,n为样本数,q为阶数,t服从n-q-2个自由度的t分布。
(4)降维和公因子提取
主成分分析试图在力保数据信息丢失最少的原则下,对这种多变量的截面数据表进行最佳综合简化。
计算贡献率,即第i个主成分的方差在全部方差中所占比重,称为贡献率 ,反映了原来P个指标多大的信息,有多大的综合能力 。计算累积贡献率:前k个主成分共有多大的综合能力,用这k个主成分的方差和在全部方差中所占比重来描述,称为累积贡献率。即:
于是在原始变量和主成分之间形成一组相关系数,用图表可以表示为:
(5)最小二乘法
已知函数y=f(x)的数据点( xi , yi )(i=0,…,m),在函数空间中,求函数(aj* 为待定系数),使拟合函数S*(x)与所有数据点的误差向量δ*的分量平方和 最小。然后求解方程如下,从而估计参数值。
四、实例研究
为了研究徐州地区经济发展各系统之间的协同性,本节选取2011-2014年徐州社会经济发展主要指标及其数据进行研究,研究所用数据采集自徐州市统计局发布的2011-2014年统计报告中。
区域经济指标系统的内涵很多,各要素的独立运动也是客观存在的,不同的指标选取会直接决定了研究的偏相关性不同。这里我们选取的11项经济运行指标在徐州市统计局发布的年报分析中重点论述的,在一段时间内它们之间的相互作用构成了序参量群。通过研究这些指标,我们可以大致了解目前徐州区域经济发展的主导模式。
2.数据处理与结果分析
本文对2011-2014年上述公布的11项经济指标进行了数据分析,首先对数据进行归一化处理,使计算规定在一个合理的范围内,同时加速计算过程的收敛。根据Z-Score方法,计算出标准化结果如下:
通过计算各项指标之间的相关系数,可以得出不同指标之间的协同系数,计算结果如下表:
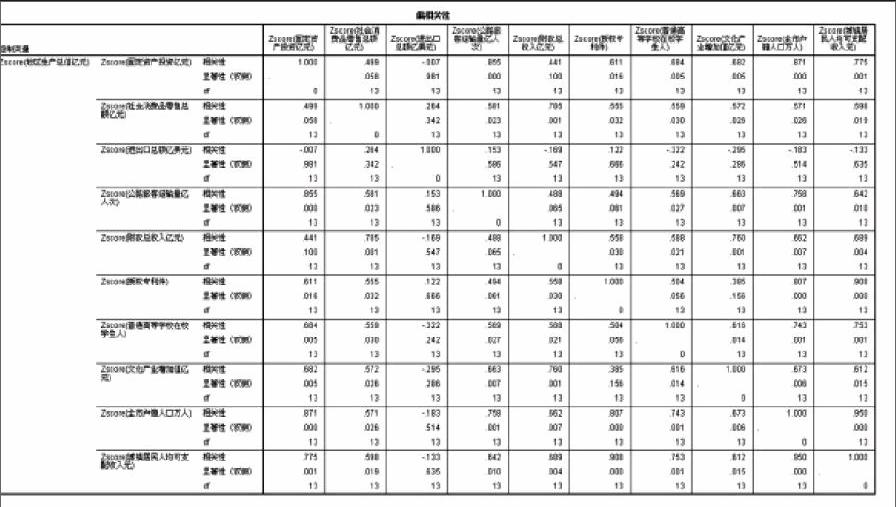
通过控制变量,对影响地区生产总值的指标偏相关性进行分析,得出不同指标与地区生产总值之间的正相关性,计算结果如下表:
根据表1、表2、表3的计算结果,可以得出:
(1)固定资产投资在拉动徐州经济增长过程中作用显著。2011-2014年,徐州经济发展,总体上呈现出上升水平,固定投资在0.05水平(双侧)上显著相关。这表明在过去的4年中,经济增长仍然主要依靠固定资产投资,固定资产投资增长较快。
(2)进出口总额在拉动徐州经济增长过程中作用不显著。这与徐州是煤炭资源型城市的特点有关,在过去4年中,对外贸易降幅收窄。相比之下,社会消费品零售总额与地区生产总值之间的偏相关性系数为0.499,未通过显著性检验,表明这一阶段徐州经济的发展,仍然主要依靠投资拉动,而非消费拉动。
(3)交通运量持续扩张,在经济发展过程中作用显著。历史以来,徐州一直是,苏北地区的交通枢纽,素有五省通衢的美称,战略位置十分重要。2011-2014年,公路旅客运输量逐年增长,与地区生产总值在0.05水平(双侧)上显著相关,经过偏相关分析,证实其与地区生产总值的增长呈现显著的正相关性。
(4)城市化水平揭示创新驱动“后劲足”。以专利授权件数和普通高等学校在校人数为代表的科技贡献率在推动区域经济发展过程中体现了较强的正相关性,新的经济增长点正在形成,传统的劳动密集型产业对经济的影响作用正在逐渐的退出历史舞台。
3.方程拟定
(1)主成分分析
KMO检验得分0.769,适合进行因子分析。Bartlett检验表明被测试数据来自服从多元正态分布的总体,本研究中Sig值为0.000,说明数据来自正态分布总体,适合进一步的分析。
进一步分析变量中所包含原始信息的公因子, 表中成分1,2累计贡献率达到82.88%,说明这两个公因子对各变量的解释能力很强。通过绘制碎石图,两个成分的特征值已超过了1,其他成分得分快速收敛。
下表给出主成分得分系数矩阵,根据此矩阵可以直接写出各公因子的表达式:
(2)探索研究
经济数据通常带有非平稳性特征,具备自相关性特点,可以通过滞后K期,观察其与时间序列的自相关性。通过高阶差分或差比的处理,首先是时间序列平稳下来,在进一步研究造成时间序列波动的原因。下面提取地区生产总值绘制散点图:
通过一阶差比图,可以看出数据序列趋于稳定,差比出现自回归特点,一直稳定在1附近,考虑使用ARCH模型描述方程。通常对滞后K期数据观察设定取值K<5,对连续4个滞期观测如下表:
进一步对单位根求解,计算滞期为1时的单位根,得到结果如下,初步分析认为以上结果具备时间序列特征,表现出高度自相关特点,适合进一步研究,以确定相关对象是随机变量本身Xτ还是ετ扰动项,此文不再探讨。
参考文献:
[1]杜志平,穆东.系统协同发展的DEA评价研究[J].运筹与管理,2005,2:75-81.
[2]杨洁,王艳,刘晓.京津冀区域产业协同发展路径探析[J].价值工程,2009(4):35-37.
[3]侯建荣,周颖,顾锋.都市圈城市经济系统的协同机理研究[J].中国管理科学,2009,10:684-687.
[4]厉以宁.区域发展新思路[M].北京:经济日报出版社,2000,28-29.
[5]许国志.系统科学[M].上海:上海科技教育出版社,2000,7-9.
[6]王力年.区域经济系统协同发展理论研究[D].东北师范大学,2007.
[7]LI Tan,L Wang,Y Wang.Research on Synergetic Development Between Efficiency of Port Logistics and Its Hinterland Economy in Liaoning Province[J]. 《Economic Geography》, 2012
作者简介:单小珂(1981-),女,江苏徐州人,硕士,江苏联合职业技术学院徐州技师分院团委,研究方向:经济管理教育。
蔺 莉(1984-),女,江苏徐州人,硕士,江苏联合职业技术学院徐州技师分院教师,研究方向:思想政治教育。
基金项目:本文系江苏联合职业技术学院2014年度立项课题“从‘零和博弈到‘正和博弈——徐州地区产业可持续发展与职业教育改革协同度研究”(编号:B/2014/06/058)的阶段性研究成果。

