贵金属价格预测的数学模型研究

杨馨园　赵颖祺　吴曼　刘进禄　徐捷　刘可　高翔

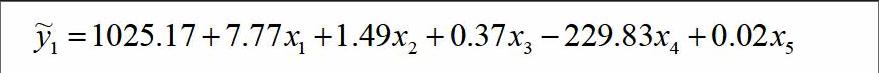
摘要：为研究贵金属价格的变化趋势，以100g现货黄金Au100g为例进行数据处理和建模。综合考虑多重因素对贵金属价格的影响，主要包括石油价格、通货膨胀（具体体现在居民消费物价指数、商品零售价格指数等）、人民币美元汇率、股票市场（具体可以体现在道琼斯指数、纳斯达克指数、沪深指数等），整合07年以来近九年的Au100g价格日数据和月度数据以及各种影响因素的相关数据。利用马尔科夫模型、神经网络、偏最小二乘分析等多种数学模型，取长补短，从长短期等多角度进行充分的数据挖掘，进而预测Au100g的价格，本文重点以人工神经网络模型展开介绍。

关键词：贵金属价格预测；神经网络；马尔科夫模型；偏最小二乘分析

中图分类号：TF83 文献识别码：A 文章编号：1001-828X（2016）012-000-04

一、模型一：马尔科夫模型

1.马尔科夫模型基本介绍

马尔科夫预测模型的构建，即利用初始状态的概率向量和状态转移矩阵来推测预测对象未来某一时间所处的状态。S（k）=S（k-1）· P=S（0）·Pk，其中，P为一步转移概率矩阵。由模型可知，第K期的状态概率取决于初始状态概率和一步转移概率矩阵的K次方。由此可见，若已知初始状态概率向量S（0）及转移矩阵P，则可求出预测对象在任一时间处于任一状态的概率。

2.马尔科夫模型的约束性[1]

运用马尔科夫预测模型对预测对象在预测期间的约束条件为：

（1）每一个时期向下一个时期的转移概率不变，均为一步转移概率；

（2）预测期间状态的个数不变；

（3）无后效性，即状态的转移仅与它前一期的状态和取值有关，而与前一期以前所处的状态和取值无关。符合上述约束条件的预测对象即构成马尔科夫过程，我们可对其建立预测模型进行预测。

但值得注意的是，由于长期来看转移概率矩阵将发生变化，马尔科夫预测法只适合于短期预测。在短期内，如果贵金属市场无特殊事件发生，运行正常，那么贵金属价格的变化过程可看作一个动态的随机过程，满足马尔科夫过程的条件，可以运用马尔科夫预测法进行价格的预测。

3.模型的建立与求解

步骤如下：

①根据历史数据推算贵金属价格的转移率，算出转移率的转移矩阵；

②统计作为初始时刻点的贵金属价格分布状况；

③建立马尔科夫模型，预测未来贵金属价格供给状况。

本文选取2015年6月-2016年2月共183个交易日的收盘价变动情况为例，将黄金价格的增长率划分为5种状态：快速增长（价格增长超过0.05%）、缓慢增长、相对不变、缓慢下降、快速下降（价格下跌超过0.05%），分别记为状态1、2、3、4、5。

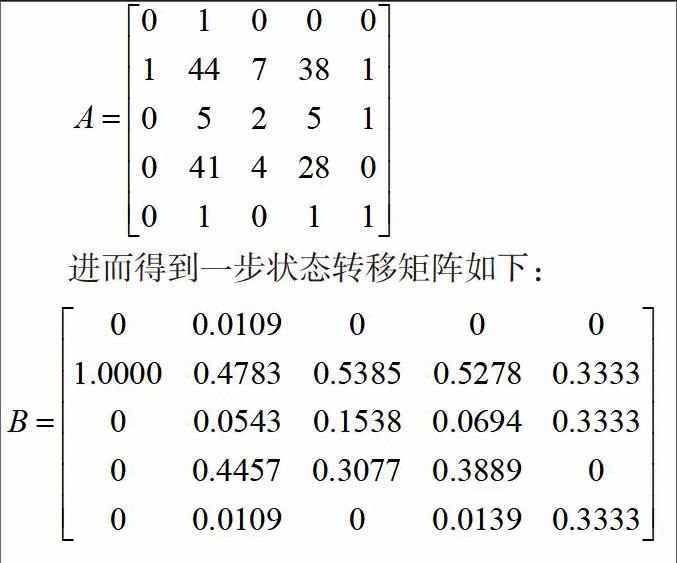
由程序运行结果知：出现各种状态的次数矩阵如下：

又因为最后一个交易日的大盘状态为4，所以预测下一个交易日黄金价格处于状态1、2、3、4、5的概率矩阵为[0 0.5278 0.0694 0.3889 0.0139]，即下一个交易日黄金价格缓慢增长的可能性最大，概率为52.78%。进而求出两补状态转移矩阵如下：

预测下一个交易日黄金价格处于状态1、2、3、4、5的概率矩阵为[0.0057 0.4997 0.0710 0.4078 0.0158]，即再下一个交易日黄金价格仍然是缓慢增长的可能性最大，概率为49.97%。但是可以看出价格处于四种状态的概率越来越接近，预测结果越来越不明显，所以表明马尔科夫模型只适用于做短期预测。

由求解结果与实际金价对比可知，运用马尔科夫方法构建的预测模型对贵金属价格的预测显示出一定的成功率。当然，也应该指出这种概率预测方法得出的结果只是表明了预测对象将来将以某一概率趋向于某种状态，而不是绝对处于这种状态，也并不能完全得到贵金属价格的具体数值。由于贵金属市场的波动是一个复杂的非线性系统，贵金属价格的变化受到了多种因素的影响，因而包括马尔科夫预测法在内的任何一种预测方法都不可能准确地预测出贵金属价格每日的变化。虽然运用马尔科夫预测法对金价作短期预测只能取得一定的效果，但其新的预测思路也颇具借鉴意义。

二、模型二：人工神经网络

1.神经网络模型基本介绍

人工神经网络是由具有适应性的简单单元组成的广泛并行互连的网络，它的组织能够模拟生物神经系统对真实世界物体所作出的交互反应。BP神经网络是训练方式为误差反向传播，激励函数为S-sigmoid函数，即为：f（x）=1/（1+exp（-x））。BP网络模型处理信息的基本原理是：输入信号通过中间节点（隐层点）作用于输出节点，经过非线形变换，产生输出信号，网络训练的每个样本包括输入向量和期望输出量，网络输出值与期望输出值之间的偏差，通过调整输入节点与隐层节点的联接强度取值和隐层节点与输出节点之间的联接强度以及阈值，使误差沿梯度方向下降，经过反复学习训练，确定与最小误差相对应的网络参数（权值和阈值），训练即告停止。此时经过训练的神经网络即能对类似样本的输入信息，自行处理输出误差最小的经过非线形转换的信息。

BP网络模型包括其输入输出模型、作用函数模型、误差计算模型和自学习模型[2]。

节点输出模型

f-非线形作用函数；q-神经单元阈值；

作用函数模型

误差计算模型

误差计算模型是反映神经网络期望输出与计算输出之间误差大小的函数，本文所采取的是残差计算方式：

其中，表示 i节点的期望输出值；表示i节点计算输出值。

学习（权值更正）模型

神经网络的学习过程，即连接下层节点和上层节点之间的权重拒阵的设定和误差修正过程。BP网络有导师学习方式-需要设定期望值和无导师学习方式-只需输入模式之分。自学习模型

表示学习因子；表示输出节点i的计算误差；表示输出节点j的计算输出；表示动量因子。

过程神经网络与一般的人工神经网络最大的不同在于，某一时刻的系统输入量不止是当前时刻的输入量，而且还包含之前某段时间的输入量，输入层节点用于接受时变的输入函数，个时变输入函数的空间加权聚合、时间累积聚合以及激励运算，并将运算结果输出至输出层；输出层也不仅接受来自隐层神经元的激励计算结果，而且直接接受来自输入层的时变输入函数信号，并将接受到的信号在进行完空间加权聚合及时间累积聚合的运算后完成系统的激励输出。

2.过程BP神经网络的模型建立

由于黄金价格的自身时间序列预测，是根据之前某段时间的价格预测之后某个时间点的价格，基于这一点思想，建立了过程BP神经网络，由于对输入量时间维度的阶数最优性的不确定，本文分别构建了1-12阶的过程神经网络，即当前系统的输入量分别为之前1-12个时刻的输入值（黄金价格），以此来构建1-12阶的过程神经网络。分别比较得到的12个神经网络的实际输出与预期输出的关系，选取其中误差最小的阶数，作为最优过程神经网络的阶数。

同时对于划分好的输入量，输出量，选取其中的百分之九十进行学习，并用剩余的百分之十进行检验，即可以防止学习不足，数据信息提取不完善，又可以做到防止过拟合，过度依赖于原数据而失去了对其他数据的处理能力。

输入量和相应输出量数据提取。在进行第阶的过程神经网络的构造时，输入量的组数为 [N/k]（其中N为总黄金价格日数据的个数），其中第组输入量为，输出量分别为。

输入量和相应输出量的归一化处理。由于数据差异性基本都在同一数量级，为了神经网络的权值不会特别受输入量，本文所采取的归一化方式为把最小值归一化为0，把最大值归一化为1，归一化公式如下：

神经网络基本结构的创建。过程BP神经网络的结构选取为，输入神经元个数等于阶数，共含有两个隐含层，每个隐含层含有五个神经元，输出神经元个数为1，基本结构如下：

神经网络的学习过程。神经网络的学习过程按照梯度下降法进行，以11阶输入为例，学习过程的相关图像如下。

随着迭代次数的残差变化情况如下：

神经网络的相关参数值的变化示意图如下：

神经网络训练45代之后，训练数据、测试数据、检验数据和全部数据分别与实际数据的相关性程度示意图如下：

利用学习的结果进行预测，并根据误差计算公式，计算分析每一阶数的预测效果。

3.模型的求解

模型求解得到阶数1-12的预测误差如下：

在此给出具有代表性的两幅预测图像：

（即综合误差最大的2阶图像、综合误差最小的10阶图像）

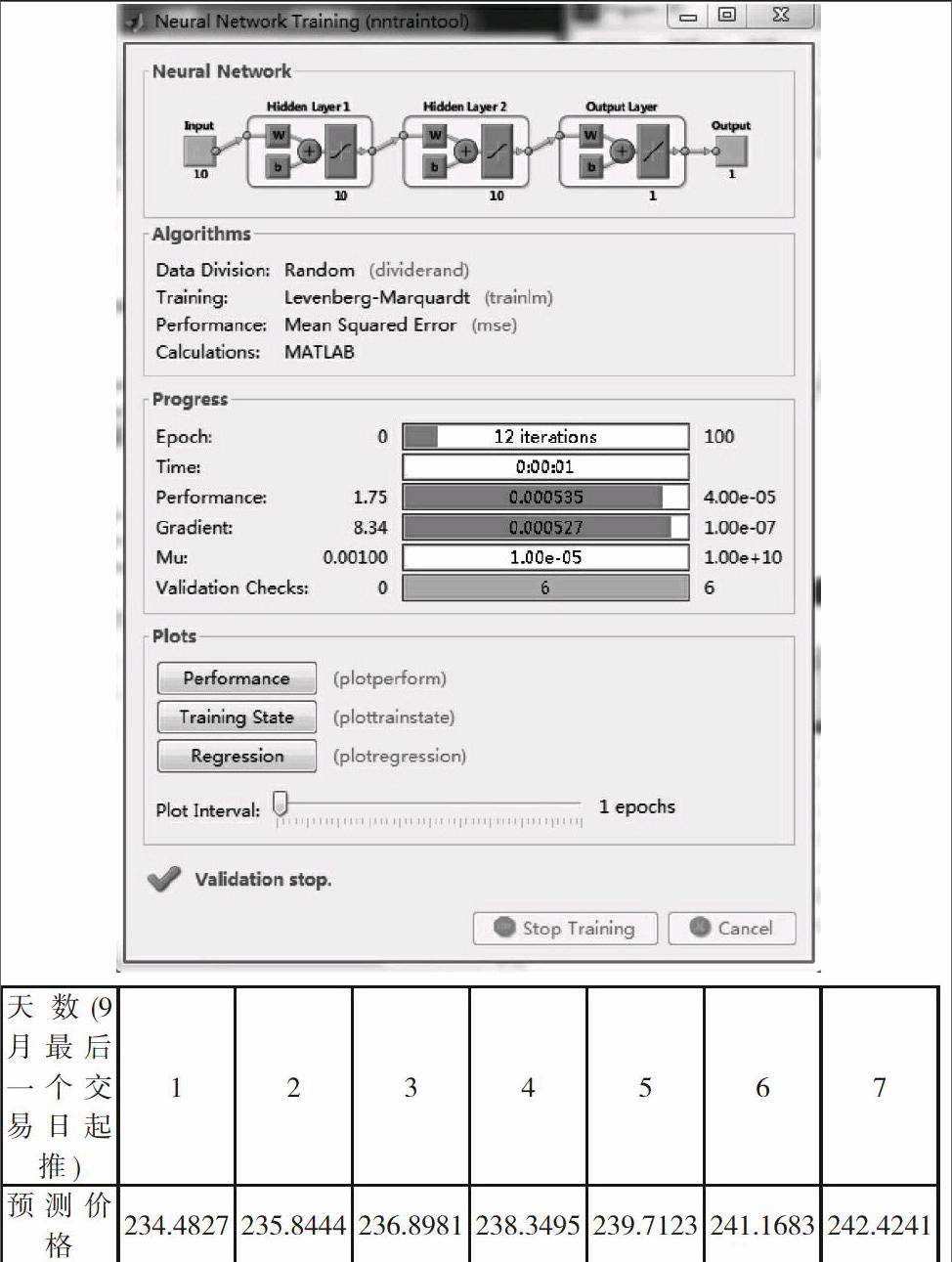
最优阶数所对应的神经网络的训练结果如下：

三、模型三：偏最小二乘法

1.偏最小二乘法基本介绍[3]

偏最小二乘法的基本公式为：

偏最小二乘回归≈主成分分析+典型相关分析+ 多元线性回归分析[4]

偏最小二乘法的基础是最小二乘法，在尽可能提取包含自变量更多信息的成分的基础上，保证了提取成分和因变量的最大相关性，即偏爱与因变量有关的部分，所以称其为偏最小二乘回归。

2.模型的建立与求解

模拟黄金价格与各因素之间的关系，变为构造一个变量与自变量之间的函数关系。通过主成分分析的方法，在自变量中提取主要成分，在因变量中提取主要成分，并且让（通过典型相关分析实现），然后进行因变量，若精度满足要求，即在本文中要求交叉有效性小于0.0985，则停止进行下一个主成分的选取。否则再继续选取第二主成分，然后进行，直到满足精度的要求。当构建完成，再得到因变量与自变量偏最小二乘方程[5]。

经Matlab程序运行后得到交叉有效性-0.1723以及主成分的系数矩阵，进而得到因变量与自变量之间的偏最小二乘回归方程：

易知三种方法的精确程度：神经网络>偏最小二乘分析>马尔科夫模型。马尔科夫模型精度最低，我们仅用该模型通过黄金价格的数据预测其变化趋势及大致浮动范围，无法加入相关因素的扰动进行分析与预测。神经网络是模拟生物神经系统对真实世界物体所作出的交互反应，因此其预测数据的拟合度最高。偏最小二乘分析法则是通过纯数理方法进行预测，相对神经网络缺少交互性。

参考文献：

[1]李海涛.运用马尔科夫预测法预测股票价格[J].统计与决策，2002（5）.

[2]张立明.人工神经网络的模型及其应用[M].上海：复旦大学出版，1993.

[3]高惠璇，著.应用多元统计分析[M].北京：北京大学出版社，2005，1.

[4]王惠文.偏最小二乘回归方法及其应用[M].北京：国防工业出版社，1999，4.

[5]何晓群.回归分析与经济数学建模[M].北京：中国人民大学出版社，1997，5.