黑子面积随黑子数变化的统计研究*

冯　雯，谢婧岚，李可军

(1. 昆明理工大学分析测试中心，云南 昆明　650093； 2. 南京大学现代天文与天体物理教育部重点实验室，江苏 南京　210093；3. 中国科学院云南天文台，云南 昆明　650011；4. 中国科学院太阳活动重点实验室 (国家天文台)，北京　100012；5. 中国科学院大学，北京　100049)



黑子面积随黑子数变化的统计研究*

冯雯1,2，谢婧岚3,4,5，李可军3,4

(1. 昆明理工大学分析测试中心，云南 昆明650093； 2. 南京大学现代天文与天体物理教育部重点实验室，江苏 南京210093；3. 中国科学院云南天文台，云南 昆明650011；4. 中国科学院太阳活动重点实验室 (国家天文台)，北京100012；5. 中国科学院大学，北京100049)

摘要：对1874年5月-2015年3月期间每月黑子数和黑子面积数进行数据分析，统计研究黑子数与黑子面积比例的变化。结果表明：黑子数与黑子面积非线性变化，在活动周极大时期更明显。二者的分布概率整体相似，都随数值增大而降低，但黑子面积下降得更明显，表明二者存在非线性关系。黑子数与黑子面积的比例在活动周极小时期约为10.2，在极大时期约为21.8，长期约为16.8。每个周的上升期和下降期确定的比例有微小差别，不同活动周确定的比例有小的差别，二者间的比例有减小的趋势。

关键词：太阳活动；黑子数；黑子面积；相关分析

黑子(相对)数是一个表征太阳活动强弱的最经典、最常用的量，由沃尔夫(R. WOLF)于1848年提出，因此有时也称沃尔夫(黑子相对)数。其定义为：R=k(10g+f)，式中g是日面上黑子群的群数；f是单个黑子数；k是一个与观测仪器、方法、天气条件、观测者的经验等因素有关的换算因子。之所以出现10，是因为黑子的 “群” 比 “个” 更容易观测与确定，因而要占有更大的权重使定义量可靠[1-2]。一般群里有几 “个” 到数十 “个” 黑子，取得太大， 如100， 又掩盖了 “个” 的作用。黑子数也叫国际黑子(相对)数，现在由全球各天文台观测资料综合得出每天的值，由太阳影响数据分析中心(Solar Influences Data Analysis Center, SIDC)代表世界数据中心(World Data Center)发布[3]。黑子数在天文学、地球科学、大气科学等很多领域有广泛应用。黑子面积是另一个经常用来表征太阳活动的量，从物理意义上讲，它是更好的量[2]。黑子面积定义为黑子在日面(太阳视圆面)的面积投影改正到日面中心以太阳半球面积的百万分之一为单位的数值[2,4]。早期连续的黑子面积数据由皇家格林威治天文台(Royal Observatory, Greenwich, GRO)提供，始于1874年5月，止于1976年12月，之后主要由美国空军/美国国家海洋和大气管理局(USAF/NOAA)提供。文[2]用1874年5月到1976年12月的平滑黑子数(R)和平滑面积数(S)研究二者间的关系，发现S=16.7R+4。若使用1977年1月至2014年8月的美国空军/美国国家海洋和大气管理局数据，S=11.2R。因此皇家格林威治天文台和美国空军/美国国家海洋和大气管理局的黑子面积数之间有一个转换因子16.7/11.2=1.39。将后者转变到前者系列后合成的黑子面积数据(GRO/USAF)由马歇尔太空飞行中心(Marshall Space Flight Center, NASA)网站管理更新。

尽管二者都被用来代表太阳活动，但二者间的关系复杂。有学者认为，虽然每天的R和S似乎无关联，但从年平均值来看，S=16.7R。也有学者认为，S/R值可能与太阳活动的相位有关，并不像年均值一样，是个常数[4-5]。文[6]用交叉递归图(Cross Recurrence Plot, CRP)方法研究了二者间的相位关系，发现相位在7～12年时间尺度高度同步，但在高频相位混杂；在太阳活动周极大极小时刻比其它时刻更不同步。文[7]研究了黑子面积与黑子数比对太阳辐射的影响以及黑子面积观测资料的可靠性。该文认为二者的比例代表了黑子个体对黑子群的汇聚度和黑子的平均尺度，也反映了黑子相对光斑对太阳辐射的贡献。因此研究二者间比例的变化是有意义的。文[8-9]将黑子面积与黑子数的比定义为一个新的量：黑子单元面积，研究该量的时间演化。本文从统计的角度探讨二者在太阳周不同时刻、不同太阳周的关系。

1黑子数与黑子面积的关系分析

1.1数据

1874年5月-2015年3月期间每月黑子面积数是合成后的 GRO/USAF黑子面积数据，同时期的黑子数来自太阳影响数据分析中心，如图1。图中，为图视清晰，黑子面积被16.7除了。黑子数和黑子面积在活动周极大时期的差别比其他时期显著大，表明二者间的关系可能是非线性的。

图2给出了黑子数和黑子面积的概率分布。二者的分布很相似：概率与数目成反比，小的黑子数和黑子面积出现的概率高。黑子面积的概率似乎随黑子面积下降得更快，预示二者的非线性关系。

图1　1874年5月-2015年3月期间黑子数(实线)和黑子面积数(点线， 被缩小了16.7倍)

图2　黑子数(上图)和黑子面积数(下图)的分布概率

1.2黑子数与黑子面积的非线性关系

图3给出黑子面积随黑子数变化关系的散点图。对其进行线性拟合，得到二者的关系为S=16.793R-82.4。相关系数高达0.923，表明这种线性关系具有统计意义。图3表明，随着黑子数增大，数据越弥散。接下来用二次函数对它们进行拟合，结果为：S=0.0094R2+15.292R-49.6，相关系数为0.944。黑子数较小时，两个拟合线非常接近，线性描述是恰当的。随着黑子数增大，二次项曲线越来越高于直线，差别越来越大，非线性更明显。随着黑子数增多，黑子面积增长得更明显。这就是说，在活动周极大时期黑子数与黑子面积的非线性更明显。

图3　黑子面积数随黑子面积变化(叉号)的线性拟合(实线)和二次项拟合(虚线)

R=0时，表示没有黑子出现在日面，这时S应该为0，但线性拟合表达式中出现了一个截距值-82.4。这个值相对于所有黑子面积的实测值非常小。R=4.9时，S=0，线性拟合表达式中一次项和截距项相等。对于所有黑子数的实测值，R=4.9是非常小的，一次项经常远高于截距。因此，统

计上讲，截距对斜率偏离比例值(没有待确定的常数项时一次项的待定系数)的影响很小。由线性拟合的斜率知道，二者间的比例约为16.8。

为了判断二次项是否真的统计存在，对原始1 690个数据对， 每次随机选取1 500对，分别进行线性和二次项拟合。这个过程重复5 000次，得到相关系数的分布如图4，全部的拟合结果有统计意义。只有两次，线性和二次拟合的相关系数相等，其他都是二次拟合的相关系数高。图5给出了二次项系数的分布，小于等于0的情况只有29次。拟合结果为，S=(16.792 ± 0.217)R-82.3 ± 8.3,S=(9.339 ± 3.581)×10-3R2+(15.307 ± 0.495)R-49.8 ± 8.4。二次项系数的平均值是方差值的2.6倍多，这就是说，偏离平均值约2.6倍方差时，系数还是大于0，因此二次项是统计存在的。

1.3黑子数与黑子面积的比例随黑子数变化的关系

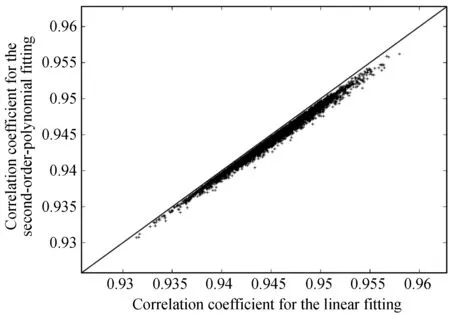
图4　线性拟合与二次项拟合的相关系数的比对。每次从黑子数和黑子面积数据对中随机取1 500对进行线性和二次项拟合，得到它们的相关系数(加号)，重复5 000次

首先对小于等于10(即截至10)的黑子数与对应黑子面积数据进行线性拟合。第2次对小于等于15(截至15)的黑子数与对应黑子面积进行拟合，黑子数每次增加5与对应黑子面积进行拟合，这样就得到拟合直线的参数(截距与斜率)随所用黑子数变化的关系，如图6。在图中，所用黑子数表示为所用黑子的截止数(每次拟合都从零黑子数开始)。拟合的相关系数在图中给出。图7给出每次计算涉及的数据个数。截止黑子数从10增加到约100，相关系数快速增加，数据点数快速增加，因此拟合结果的置信度快速增长，线性关系也快速增强。之后，截止黑子数再增加，相关系数和数据点数的增加都放缓，线性关系的增强也放缓。第1次拟合的截距为-7.22，斜率为10.28，黑子数为0.7时，拟合表达式中一次项和截距项相等，因此统计上讲，截距对斜率偏离比例值的影响很小。因此，在活动周的极小时期，二者的比例约为10.28。随着黑子数增加，例如从开始的10增加到100，截距的绝对值增加到69.55，斜率增加到16.34。这时，黑子数为4.2时，比例项和截距项相等，统计上讲，截距对斜率偏离比例值的影响仍然很小。之后，黑子数增加，截距的绝对值增加缓慢，截距对斜率偏离比例值的影响越来越小。

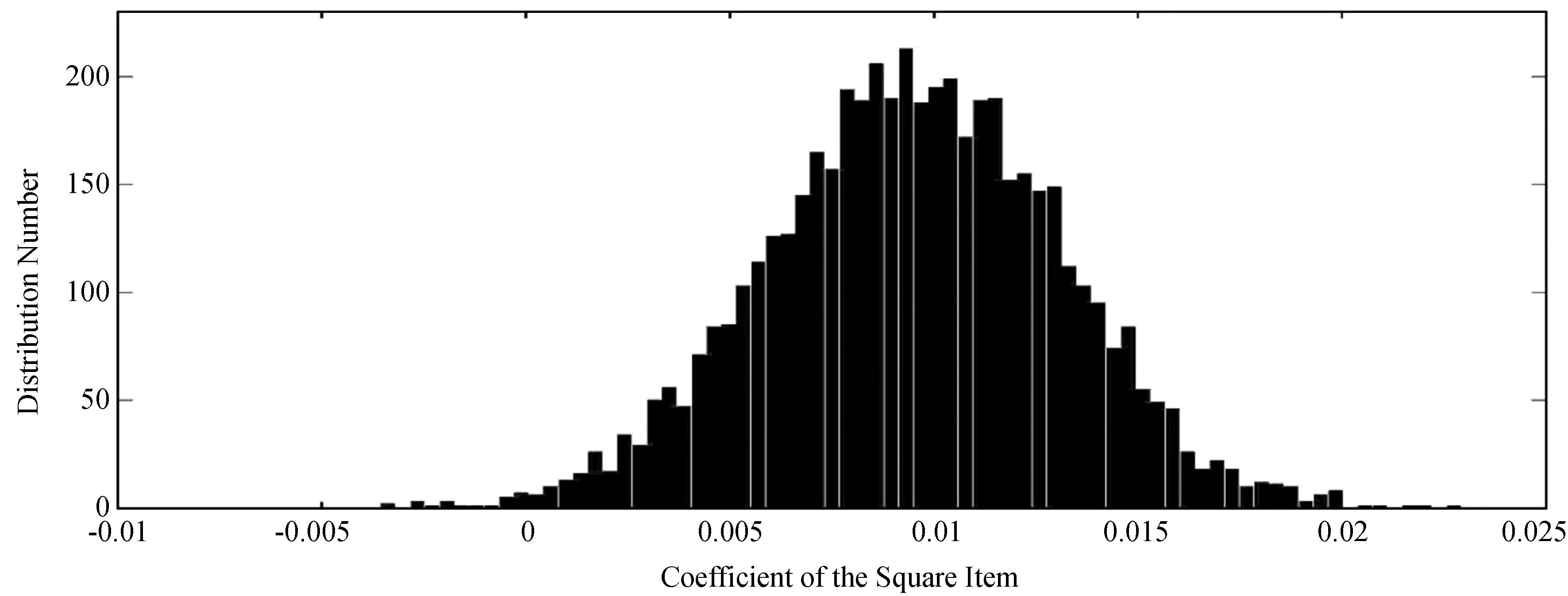
图5　5 000次对黑子数和黑子面积数据对进行二次项拟合得到的二次项系数值的分布。每次从总的1 690个数据对中随机取1 500对

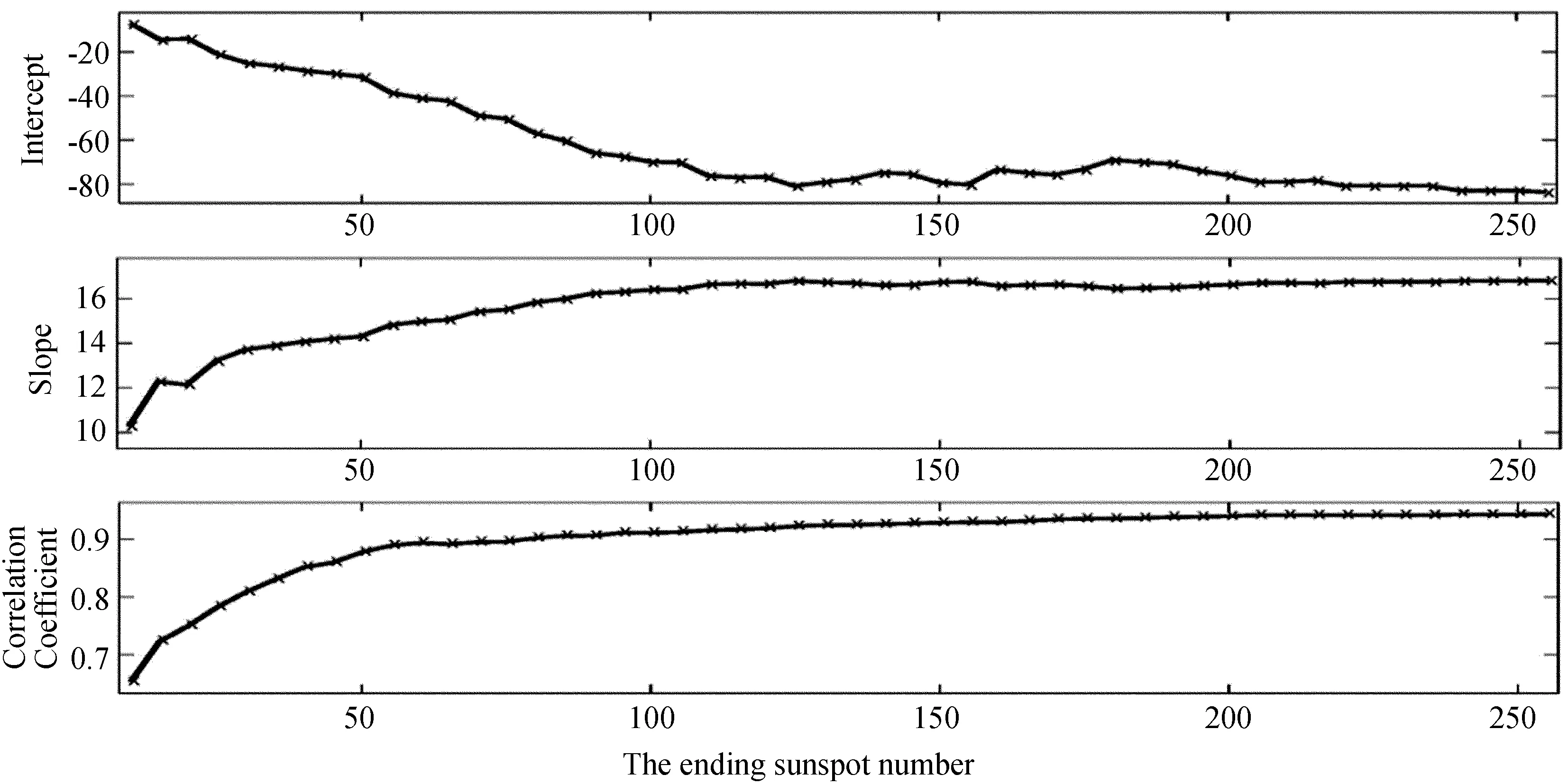
图6　在不同黑子数与黑子面积数据对长度下的线性拟合结果(叉号)：截距(上框图)，斜率(中间框图)，以及拟合的相关系数(下框图)。横坐标表示截止的黑子数，每次从零黑子数开始

接下来先对全部黑子数(即始于0)与面积数据进行拟合，第2次对大于等于5(始于5)的黑子数与对应黑子面积进行拟合，第3次对大于等于10(始于10)的黑子数与对应黑子面积进行拟合， 开始的黑子数每次增加5与对应黑子面积进行拟合，这样就得到拟合直线的参数(截距与斜率)随所用黑子数变化的关系，如图8。在图中，所用黑子数表示为所用黑子数的开始数值(每次拟合所用黑子数都截止到最大黑子数)。相关系数也在图中给出。图9给出每次计算涉及的数据对的个数。最后一次计算的开始黑子数为145，所用数据对的数目为92(图中最小值)，相关系数为0.654(图中最小值)，线性拟合有统计意义，因此各次计算结果都有统计意义。图8显示，从R=105开始， 截距的绝对值随开始黑子数有一个较大的增加。开始黑子数为105时，拟合结果为S=17.516R-168.394。S=0，则R=9.61，比开始黑子数小得多，因此截距对斜率偏离比例值的影响很小。最后一次计算，开始黑子数为145，这时S=21.811R-920.962。S=0，则R=42.2，比开始黑子数小很多，因此截距对斜率偏离比例值的影响较小。二者间的比例约为21.8。

图7　在黑子数与黑子面积数据对不同长度下进行线性拟合时每次计算所用数据对的个数(叉号)。每次计算都从最小黑子数开始，横坐标表示的是每次计算截止的黑子数

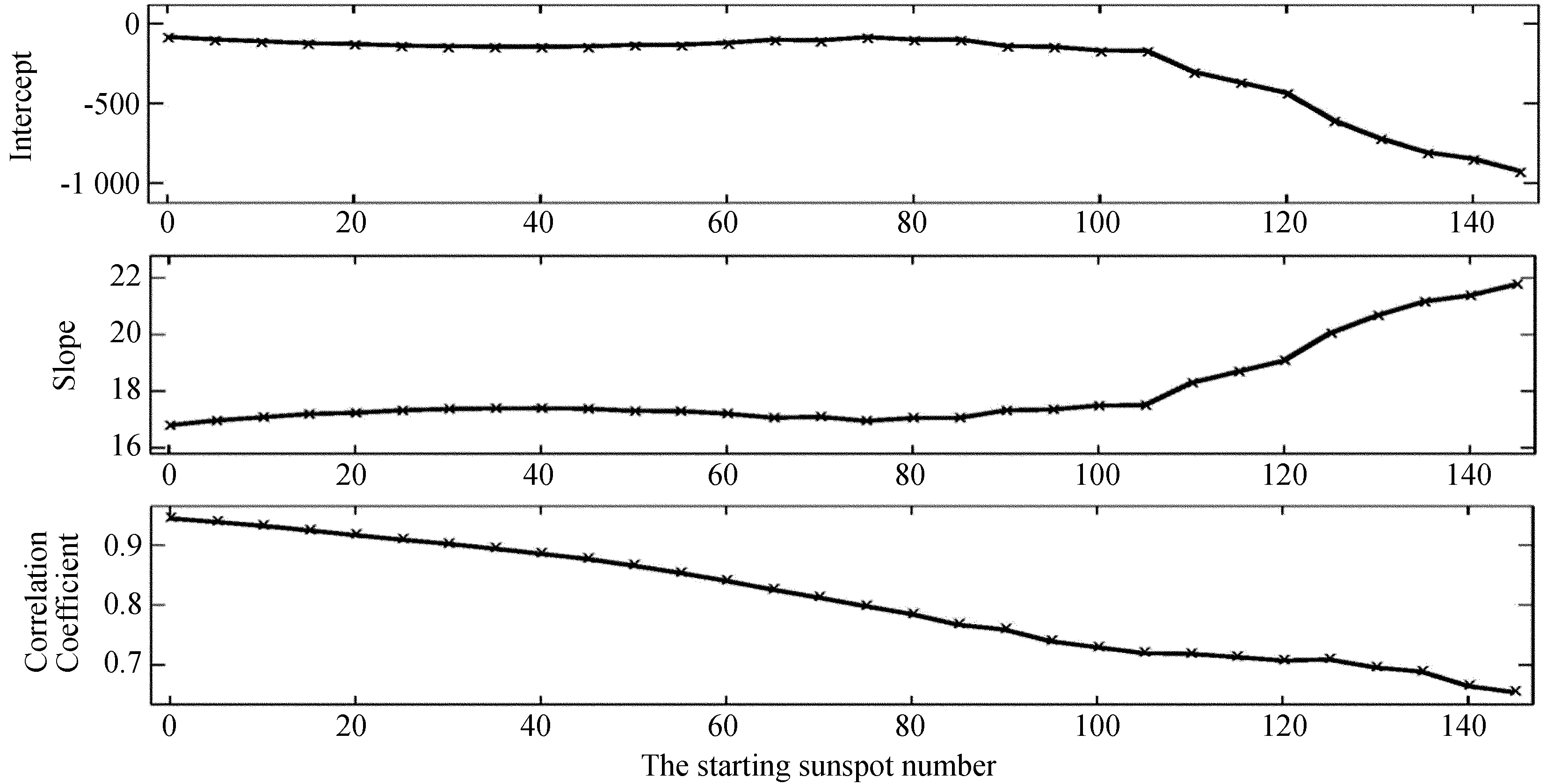
图8　在不同黑子数与黑子面积数据对长度下的线性拟合结果(叉号)：截距(上框图)，斜率(中间框图)，以及拟合的相关系数(下框图)。横坐标表示开始时的黑子数，每次计算所用黑子数都截止到最大值

1.4黑子数与黑子面积的比例随活动周变化的关系

数据完整涵盖了12～23太阳活动周。对12个活动周的每个周，分上升期、下降期和完整周3种情况进行黑子数与黑子面积数的线性拟合，所得拟合参数(截距与斜率)和拟合相关系数如图10。由图知，截距对斜率偏离比例值的影响较小。每个周的上升期和下降期确定的二者间的比例(斜率)有微小差别，不同活动周确定的比例有小的差别。对各个活动周确定的比例(slope)随活动周变化(cyc)

的关系进行线性拟合，得到相关系数为0.518，在92%置信水平有意义，slope=20.919-0.201cyc，因此比例有随活动周减小的趋势。对各个周确定的3种比例(斜率)分别与各个周的极大黑子数和周长进行相关分析， 发现它们并不关联。

2结论与讨论

本文利用1874年5月-2015年3月期间皇家格林威治天文台/美国空军提供的每月黑子面积数和太阳影响数据分析中心提供的国际黑子数数据，统计研究二者比例的变化。二者的分布概率整体上很相似，但还是有区别的，黑子面积的分布概率随黑子面积的增大而下降得更激烈。分布概率的不同将导致二者间出现非线性。二次项拟合表明二者间的确是非线性的，且非线性在活动极大期间更明显。在活动极大时期，二项拟合值大于对应的线性拟合值，表明黑子的平均尺度在此期间比其他时间更大。

图9　在黑子数与黑子面积数据对不同长度下进行线性拟合时每次计算所用数据对的个数(叉号)。横坐标表示开始时的黑子数，每次计算所用黑子数都截止到最大值

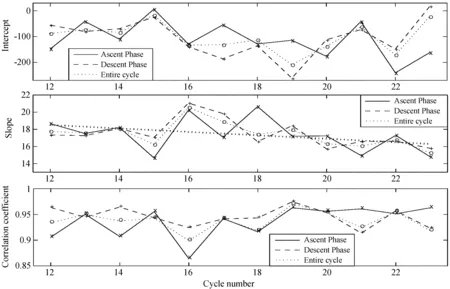
图10　利用活动周上升期(叉号和实线)、下降期(虚线和加号)和整个周(点线和圆圈)数据3种情况下进行黑子数与黑子面积数的线性拟合，所得拟合线的截距(上框图)、斜率(中间框图)和拟合相关系数(下框图)

对黑子数不同长度的数据与黑子面积进行比对，研究二者间的关系在活动周的不同时刻的变化。黑子数与黑子面积的比例在活动周极小时期约为10.2，在极大时期约为21.8，长期看，约为16.8。比例在黑子数小时波动的幅度比在极大时期小。每个周的上升期和下降期确定的比例有微小差别，不同活动周确定的比例有小的差别。比例值随太阳周的变化并不与各个周极大值和周长随太阳周的变化相关联。二者间的比例有减小的趋势。

参考文献：

[1]Wolf R. Abstract of his latest results[J]. Monthly Notices of the Royal Astronomical Society, 1861, 21: 77-78.

[2]Hathaway D H. The solar cycle[J]. Living Reviews in Solar Physics, 2010, 7(1): 1-76.

[3]冯雯, 李可军. 交通事故发生受太阳活动影响吗?[J]. 天文研究与技术——国家天文台台刊, 2014, 11(2): 192-200.

[4]张明昌, 肖耐园. 天文学教程 (上册) [M]. 北京: 高等教育出版社, 1987: 452.

[5]胡中为. 普通天文学[M]. 南京: 南京大学出版社, 2003: 289.

[6]Li K J, Gao P X, Zhan L S. Synchronization of sunspot numbers and sunspot areas[J]. Solar Physics, 2009, 255(2): 289-300.

[7] Fligge M, Solanki S K. Inter-cycle variations of solar irradiance: sunspot areas as a pointer[J]. Solar Physics, 1997, 173(2): 427-439.

[8]Li K J, Qiu J, Su T W, et al. Sunspot unit area: a new parameter to describe long-term solar variability[J]. The Astrophysical Journal, 2005, 621(1): L81-L84.

[9]Li K J, Xiang N B, Qu Z N, et al. Hemispheric sunspot unit area: comparison with hemispheric sunspot number and sunspot area[J]. The Astronomical Journal, 2014, 147(3): 367-372.

A Statistical Study on Sunspot Area Varying with Sunspot Number

Feng Wen1,2, Xie Jinglan3,4,5, Li Kejun3,4

(1. Research Center of Analysis and Test, Kunming University of Science and Technology, Kunming 650093, China;2. Key Laboratory of Modern Astronomy and Astrophysics (Nanjing University), Ministry of Education, Nanjing 210093, China;3. Yunnan Observatories, Chinese Academy of Sciences, Kunming 650011, China; 4. Key Laboratory of Solar Activity, National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100012, China, Email: lkj@ynao.ac.cn; 5. University of Chinese Academy of Sciences, Beijing 100049, China)

Abstract:Statistical relation of sunspot area varying with sunspot number has been investigated through analyzing sunspot area and sunspot number with data acquired from May 1874 to March 2015. The obtained results are: (1) in general, distribution probabilities of both sunspot number and sunspot area are similar to each other; they decrease along with the increase of value; but the probability of sunspot area decreases more obviously, which implies that a non-linear relation between the two exists; (2) the non-linear relation is more clear during the solar maximum; (3) the ratio of sunspot area to sunspot number is about 10.2 during the solar minimum, 21.8 during the solar maximum, and 16.7 on long-term basis; (4) the ratio of every ascent phase is slightly different from that of the descent phase, and the determined ratios of different solar cycles are different from one another, displaying little relation to both the maximum amplitudes of cycles and cycles lengths; and (5) the ratios tend to decrease with increasing cycle number.

Key words:Solar activity; Sunspot number; Sunspot area; Correlation analysis

基金项目：国家自然科学基金 (11273057, 11221063)；国家重点基础研究发展计划 (2012CB957801, 2011CB811406)以及现代天文与天体物理教育部重点实验室开放基金课题资助项目.

收稿日期：2015-05-14；

修订日期：2015-06-14

作者简介：冯雯，女，工程师. 研究方向：日地关系物理. Email: fengwen69@sina.cn 通讯作者：李可军，男，研究员. 研究方向：日地关系物理. Email: lkj@ynao.ac.cn

中图分类号：P182

文献标识码：A

文章编号:1672-7673(2016)02-0153-07

CN 53-1189/PISSN 1672-7673