CCD图像拼接试验*

阳　强，彭青玉

(1. 暨南大学计算机科学系，广东 广州　510632；2. 暨南大学中法天体测量、动力学与空间科学联合实验室，广东 广州　510632)



CCD图像拼接试验*

阳强1,2，彭青玉1,2

(1. 暨南大学计算机科学系，广东 广州510632；2. 暨南大学中法天体测量、动力学与空间科学联合实验室，广东 广州510632)

摘要：为了获得大视场的高精度天文图像，实施了一种望远镜CCD图像的拼接方法。从原始图像到最终合成图像的坐标转换采用了结合星表UCAC4的六常数模型。不同于硬件级的拼接，使用逐个像素的灰度值再分配的方案进行图像融合。进一步采用云南天文台2.4 m望远镜拍摄的CCD图像进行了试验。结果表明，该算法可以产生较高质量的大视场CCD图像，可以直观地发现运动目标，暗星信噪比有显著改善。高精度的图像拼接还与原始数据扭曲改正的预处理密不可分。与未做扭曲改正相比，图像拼接的位置精度提高了约一倍(约0.02 pixel)。

关键词：拼接；大视场；几何扭曲；CCD图像

长焦距望远镜观测得到的小视场(如5′ × 5′)CCD图像常常出现目标区域参考星不足的问题[1]，这是由参考星太暗或参考星数太少造成的。文[2-3]用重迭露光观测获得一系列CCD图像，然后将这些来自不同平面的图像归算到同一天球面，解决了小视场天体测量定标的问题。类似地，局部平差方法也能较好地解决这一问题[4]。但是这些方法的归算过程比较复杂。本文直接用CCD图像拼接得到大视场的图像并能用于高精度的位置测量。

借鉴一种称作Drizzle的图像拼接方法。这种方法最先由文[5]提出并用于拼接Hubble Deep Field-North(HDF-N)的抖动观测图片，也用于其他望远镜拍摄的CCD图像[6]。Drizzle使用平移相加能确保高分辨率[7]。也有其他一些线性拼接图像的方法，如文[8]的方法，文[9]的Imcom方法，文[10]的iDrizzle方法以及文[11]的直接模型拟合拼接方法。

哈勃空间望远镜(Hubble Space Telescope, HST)和Spitzer空间望远镜(Spitzer Space Telescope, SST)的图像拼接可用于解决原始图像的欠采样问题[7]。地基望远镜受大气宁静度的影响，基本不会欠采样。不需要通过亚像素级的抖动观测，只需采用简单的平移和灰度值相加，就能保持拼接图像的高保真和光学统计[7]。如文[8]所述，由于光学设备的设计(如透镜受重力的影响)会造成图像的扭曲，所以各个位置的灰度值未必是其真实灰度值。因而对图像做扭曲改正是必要的。本文采用文[12]的几何扭曲求解方法得到无扭曲图像。该方法已经成功应用于行星卫星(Phoebe)和近地小行星(Apophis)的高精度位置测量，效果显著[13-14]。

拼接图像有如下优点。第一，拼接图像能用于探测暗弱星像。在拼接的图像中，同一位置随着重叠次数的增加(相当于累积曝光时间的增加)，信噪比不断提高；第二，多帧短曝光图像拼接可以克服长时间曝光的局限，确保视场亮星不饱和溢出[15]；第三，能直观地发现运动目标[16]；最后还可以尝试将拼接图像用于高精度位置测量，弥补小视场参考星太少的缺陷。

本文第1节是算法的描述；第2节对观测资料和预处理进行说明；第3节对拼接图像的输出结果进行分析；最后一节是结论。

1算法

在Windows/Visual C++环境下设计了一款软件实现相关算法。输入是多帧FITS图像及每幅图中主要参考星(例如UCAC4星表[17])信息。星像与星表星的匹配采用了文[18]的方法，对匹配结果进行归算，求出扭曲矩阵。根据扭曲矩阵对输入图像做扭曲改正得到不扭曲的图像，方法详见文[12, 19]。如果有足够的参考星，可以使用高阶常数模型进行位置归算。但实际上，只要扭曲模型稳定，可以由密集星场观测得到的扭曲模型直接用于稀疏星图像的扭曲改正。

具体的拼接步骤如图1。输入图像可以是原始的FITS图像，也可以是去扭曲后(即扭曲改正之后)

的FITS图像。

1.1底片常数模型的求解

对于每帧CCD图像，采用六常数底片模型建立标准坐标与像素坐标的关系。该模型中包含了平移、旋转、放缩和切变等仿射变换的影响，对应于指向的不准确，微小大气折射较差改正，光行差较差改正等影响。

图1图像拼接软件的处理经过和算法

Fig.1Processing and algorithmic flow in image combination

具体地，星像天球坐标(α,δ)转换为标准坐标(ξ,η)的关系方程为

(1)

其中，(A,D)是投影平面与天球切点的天球坐标。选取图像中靠近视场中央的参考星理论位置作为切点坐标。

六常数模型是指标准坐标(ξ,η)和像素坐标(x,y)的关系，关系方程为

(2)

其中，a、b、c、d、e、f是6个底片常数。实际上，采用最小二乘拟合求解(2)式中的6个底片常数。

1.2像素坐标转换

选取观测天区中靠近中心部分的图像作为基准图像，将所有其他图像转换到基准图像。图2是转换过程的流程图。具体地，对待转换图像的每一像素点的位置，由(2)式计算其标准坐标，由(1)式的逆运算再转换到天球坐标，进而从天球坐标转换到基准图像中，得到它们在基准平面的像素位置。其中，(A,D)和(A0,D0)分别是输入图像的切点和输出图像的切点。

1.3像素灰度值的分配

经过上述坐标转换后，一个输入像素点的位置被转换成基准图像的位置时，它的像素坐标不一定是整数。该像素的灰度值被分配到4个相邻的像素中。如果感光器的填充因子为100%，可以按照该像素在基准图像中覆盖不同像素的面积大小进行灰度值的比例分配。通过上述计算，把整幅输入图像的各像素的灰度值分配给输出像素，输出图像(即基准图像)就获得了该图像的灰度信息。继续处理下一幅图像时，在输出图像原有的灰度值上继续累加。随着累加的层数不断增加，灰度值也越来越大。为了归一化，将灰度值除以拼接图像的帧数使整个输出图像各个位置灰度值转换到相同的曝光水平。

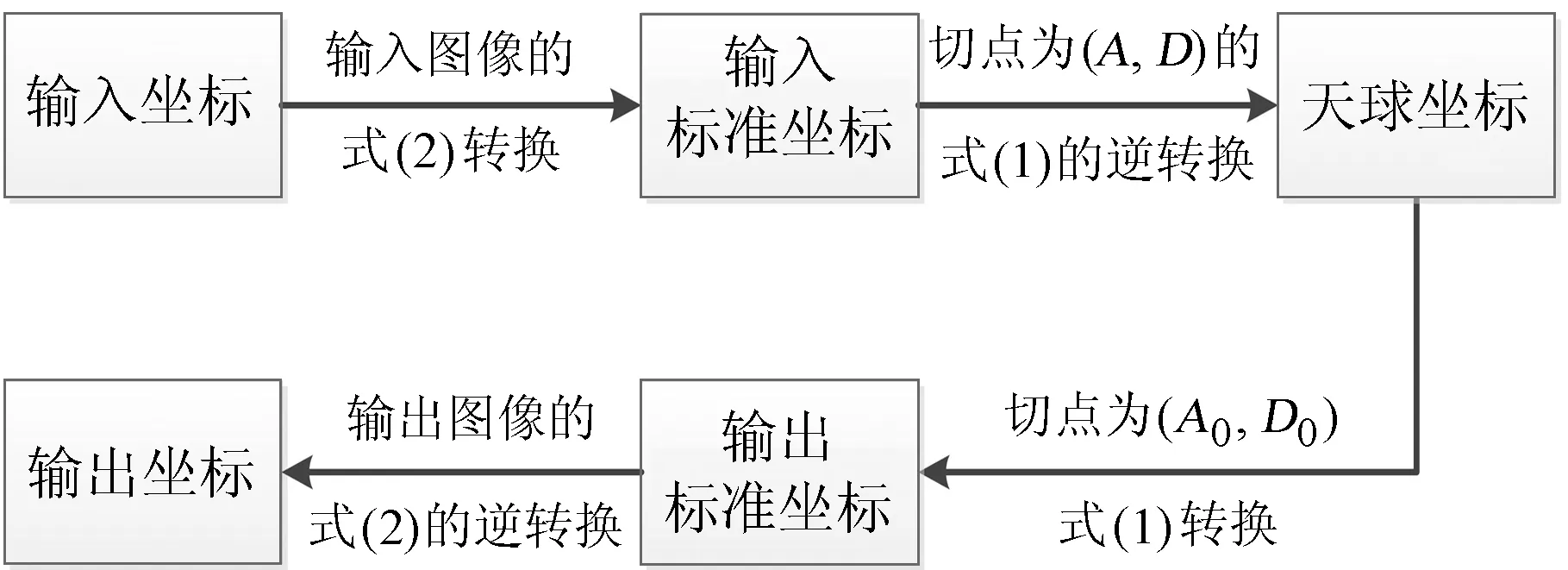
图2坐标转换过程

Fig.2Procedure of coordination transformation

2观测资料

使用的观测资料是丽江2.4 m望远镜(观测终端为YFOSC)于2013年2月5日拍摄的共计58幅抖动观测的CCD图像。云南暗天体相机及分光仪(Yunnan Faint Object Spectrograph and Camera, YFOSC)的主要参数见表1。YFOSC采用背照式CCD，该CCD结合了一个极低噪声的放大器。

表1　YFOSC的主要技术参数

每帧图像的曝光时间均为30 s，并采用B滤光片。由于抖动观测，有些星像多次重复出现在不同图像中，同一星像最多被观测51次。做平场处理并裁剪后的图像大小为1 900 pixel × 1 900 pixel，约9′ × 9′。用文[12]的方法迭代计算得到受扭曲的图像的扭曲量进而改正得到不受扭曲的图像。

3结果及分析

图3左边子图是由所有58幅不受扭曲的输入图像拼接得到的输出图像，它的大小是4 478 pixel × 4 137 pixel，周围空白部分是没有拍摄到的部分。图3右边子图是左边中间黑色矩形部分的放大。由于Apophis的运动轨迹接近于一条直线，并且拼接图像中刚好有拍成一列的多个星像，经与历表比较，证实确为Apophis的轨迹。图像拼接相当于把多帧图像的信息累加来增长曝光时间，这种增长与重叠层数成正比。考虑到泊松统计规律，图像的拼接相当于增加了曝光时间，因此，信噪比显著提高。这种增加信噪比的方法避免了长曝光观测导致亮星饱和溢出。如图4，随机选取输出的拼接图像(右边)的一块区域与原始的单幅输入图像(左边)的同区域作比较。用短曝光拍摄时，星像非常模糊，有时根本无法识别。例如，输入图像(图4左边)加圆圈部分看似只存在一些噪声，但输出图像(图4右边)的星像明显清晰可见。通过测光发现，在拼接图像中最暗的星像星等估计约22等(B星等)。用SAOImage DS9*http://ds9.si.edu/doc/ref/index.html天文图像软件绘制该星像在不同输入图数量的拼接图像中的光度分布曲线。如图5，显示了4个沿着X轴方向的光度分布曲线，纵坐标表示计数值，横坐标表示X轴坐标(刻度范围17个像素)。4子图分别为单幅原始图像、5幅重叠拼接后、10幅重叠拼接后和所有(58幅)图像拼接后的灰度分布。明显地，重叠层数越多，即便是暗星的形状也逼近高斯分布。Y轴方向的光度分布具有类似的规律。

图3不受扭曲输出图像及其局部放大后的细节

Fig.3The output image and the partial enlarged details

图4输入图像(左边)和拼接图像(右边)

Fig.4The input image (left) and the combination (right)

图5不同输入帧数拼接的某暗星的光度分布曲线

Fig.5Curve of intensity distribution of a faint under different input-frame numbers of combination

下面研究图像扭曲改正对拼接图像的影响。根据星表UCAC4对每一幅CCD图像中的星像进行归算，可将输入图像的每个星像的量度坐标换算成在输出图像中的量度坐标。由于每个星像会出现在不同的输入图像中，就有多个量度坐标，将这些量度坐标换算到基准平面并取平均值作为它的理论位置。然后求出每个星像在拼接图像中搜索的位置，并计算它与理论位置之差。在x方向(赤经方向)和y方向(赤纬方向)的搜索位置与理论位置的差分别简记为Δx和Δy，单位为pixel。对重叠充分次数的视场中央区域计算Δx和Δy，实验结果如图6，除了个别暗星偏得比较大以外，其余偏差都很小，Δx和Δy的期望值在± 0.02 pixel之内。对于受扭曲的拼接(输入图像是受扭曲的)，Δx和Δy的标准差分别是0.027 pixel(约8 mas)和0.029 pixel。而对于去扭曲的拼接(输入图像做了扭曲改正)，Δx和Δy的标准差分别减小到了0.014 pixel和0.018 pixel。可见扭曲改正的效果明显。当然，这里的误差仅代表拼接过程引入的误差，并非最终的测量精度。图7是输入图像与拼接图像的星像位置残差的标准差(SD)。从中也反映出扭曲改正对拼接结果的影响显著。有几个点的标准差偏高，这是输入图像间的某些重叠部分背景差异较大或有运动目标穿过星像造成的。

图6拼接图中的像位置与计算位置的偏差

Fig.6The deviation between the imaging position of combination and the calculated position

图7拼接图像中星像的标准差

Fig.7Standard deviation of stars in the combination

4结论

本文尝试了高精度CCD图像的拼接。试验发现，经扭曲改正后的图像能得到良好质量的拼接图像。具体表现在暗星数量的增多和信噪比的明显改善，运动目标更易识别。但计算效率需要优化改进。完成58幅图的拼接时，双核4 G内存的计算机运行耗时长达10多分钟。速度慢是因为迭代计算是逐像素的插值整合，每次整合都涉及坐标的计算和插值相交面积的计算，而每幅图又有数百万的像素。另外，将继续进行背景匹配的研究，进一步提高精度。

致谢：感谢中国科学院云南天文台丽江观测站2.4 m望远镜运行组全体员工的帮助和支持。

参考文献：

[1]Pascu D. Long-focus CCD astrometry of planetary satellites[C]// Proceedings of the 172nd Symposium of the International Astronomical Union. 1996: 373-388.

[2]Peng Q Y, Vienne A, Han Y B, et al. Precise calibration of CCD images with a small field of view[J]. Astronomy & Astrophysics, 2004, 424(1): 339-344.

[3]Peng Q Y, Zhang Q F. Precise positions of Phoebe determined with CCD image-overlapping calibration[J]. Monthly Notices of the Royal Astronomical Society, 2006, 366(1): 208-212.

[4]Yu Y, Tang Z H, Li J L, et al. Block adjustment of a group of overlapping CCD images[J]. The Astronomical Journal, 2004, 128(2): 911-919.

[5]Williams R E, Blacker B, Dickinson M, et al. The Hubble Deep Field: observations, data reduction, and galaxy photometry[J]. The Astronomical Journal, 1996, 112: 1335-1389.

[6]Makovoz D, Khan I. Mosaicking with MOPEX[C]// Astronomical Data Analysis Software and Systems XIV ASP Conference Series. 2005: 81-85.

[7]Fruchter A S, Hook R N. Drizzle: a method for the linear reconstruction of undersampled images[J]. Publications of the Astronomical Society of the Pacific, 2002, 114(792): 144-152.

[8]Lauer T R. Combining undersampled dithered images[J]. Publications of the Astronomical Society of the Pacific, 1999, 111(756): 227-237.

[9]Rowe B, Hirata C, Rhodes J. Optimal linear image combination[J]. The Astronomical Journal, 2011, 74: 1-25.

[10]Fruchter A S. A new method for band-limited imaging with undersampled detectors[J]. Publications of the Astronomical Society of the Pacific, 2011, 123(902): 497-502.

[11]Mahmoudian H, Wucknitz O. Direct model fitting to combine dithered ACS images[J]. Astonomy & Astrophysics, 2013, 556(7): 629-635.

[12]Peng Q Y, Vienne A, Zhang Q F, et al. A convenient solution to geometric distortion and its application to Phoebe′s observations[J]. The Astronomical Journal, 2012, 144(6): 1-10.

[13]Peng Q Y, Wang N, Vienne A, et al. Precise CCD positions of Phoebe in 2011-2014[J]. Monthly Notices of the Royal Astronomical Society, 2015, 449: 2638-2642.

[14]Wang N, Peng Q Y, Zhang X L, et al. Precise CCD positions of Apophis in 2013[J]. Monthly Notices of the Royal Astronomical Society, 2015, 454(4): 3805-3809.

[15]张西亮, 刘忠, 钱声帮. 恒星系统中暗弱伴星的高分辨率成像探测[J]. 天文研究与技术——国家天文台台刊, 2008, 5(4): 349-354.

Zhang Xiliang, Liu Zhong, Qian Shengbang. Detection of faint objects in multiple-star systems with high resolution image reconstruction techniques[J]. Astronomical Research and Technology

——Publications of National Astronomical Observatories of China, 2008, 5(4): 349-354.

[16]Zheng Zhongyuan, Zhu Jin, Chen Jiansheng, et al. Astronomical image restrainable combination method and its application[J]. Progress in Natural Science, 1998, 8(3): 316-320.

[17]Zacharias N, Finch C, Girard T, et al. The fourth US Naval Observatory CCD Astrograph Catalog[J]. The Astronomical Journal, 2013, 145(2): 531-544.

[18]任俊杰, 彭青玉. 两种快速星像匹配算法的比较[J]. 天文研究与技术——国家天文台台刊, 2010, 7(2): 115-123.

Ren Junjie, Peng Qingyu, Comparison of two fast object matching algorithm[J]. Astronomical Research and Technology——Publications of National Astronomical Observatories of China, 2010, 7(2): 115-123.

[19]彭青玉, 涂兵. 求解CCD图像几何扭曲的初步结果[J]. 中国科学, 2011, 41(9): 1126-1130.

Peng Qingyu, Tu Bing. Preliminary result of solving geometric distortion for a CCD image[J]. Scientia Sinica, 2010, 41(9): 1126-1130.

An Experiment of CCD Frame-Combination

Yang Qiang1,2, Peng Qingyu1,2

(1. Department of Computer Science, Jinan University, Guangzhou 510632, China; 2. Sino-French Joint Laboratory for Astrometry, Dynamics and Space Science, Jinan University, Guangzhou 510632, China, Email: jueqiqiang@126.com)

Abstract:In order to obtain astronomic images with a wide field of view and high precision, a method of combining a few CCD (Charge Coupled Device) frames taken by a telescope is performed in this thesis. Peng et al.′s geometric distortion model is used to correct original images during the pre-processing phase. Coordinate transformation from original images to the final combined frame uses a six-parameter model together with the Catalog UCAC4. Unlike hardware image mosaic, the gray value of each pixel in the original frame needs to be redistributed to the pixels of a unique reference frame. The algorithms of this frame-combination are described in detail in this article. Furthermore, this method has been tested with many CCD frames taken by the 2.4m Telescope at Yunnan Observatories. Results show that this method can yield a quite good CCD frame with a wide field of view. Specifically, moving objects can be detected easily; in terms of faint ones, there is significant improvement in their SNR (Signal to Noise Ratio) as well. Test results also show that the star positional errors introduced by the frame-combination are reduced to about 0.02 pixels when raw CCD frames are corrected for their geometry distortions. This experiment therefore confirms the validity of Peng et al.′s geometric distortion solution and the necessity of correcting geometric distortions.

Key words:Combination; Wide field of view; Geometry distortion; CCD frames

基金项目：国家自然科学天文联合基金 (U1431227)；国家自然科学基金 (11273014) 资助.

收稿日期：2015-12-15；

修订日期：2016-01-03

作者简介：阳强，男，硕士. 研究方向：图像处理. Email: jueqiqiang@126.com

中图分类号：P123; P128

文献标识码：A

文章编号:1672-7673(2016)02-0250-07

CN 53-1189/PISSN 1672-7673