一类偏微分方程的解的Bernstein性质

胡传峰， 姬　秀

(长江大学 文理学院， 湖北 荆州 434000)



一类偏微分方程的解的Bernstein性质

胡传峰， 姬秀

(长江大学 文理学院， 湖北 荆州 434000)

摘要:在局部严格凸的超曲面M上定义了α-相对度量Gα.研究了关于Gα完备且α-Ricci 曲率有下界-N的超曲面M. 利用活动标架法及J-C-P定理,证明了当ρ满足一个四阶偏微分方程时,M一定是椭圆抛物面.

关键词:Bernstein性质; 相对极值超曲面; 偏微分方程； Euler-Lagrange方程

1引言及主要结果

设y:M→An+1是一个局部严格凸的超曲面, 由定义在一个凸域Ω⊂An上的严格凸函数xn+1=f(x1,x2,…,xn)给出.设

若Y=(Y1,…,Yn+1) 是M上的转移向量场且对任意点y∈M有dY∈TyM, 则称Y是M的相对法场.尤其, 当Y=(0,…,0,1)时,M上的余法场U和相对黎曼度量G可分别定义为

G也被称为Calabi度量. 记

李安民院士首先研究了M上由Uα=ραU诱导的相对法场. 在文献[1]中此相对法场被称作α相对法场, 后来在文献[2-4]中也被称作李法场. 相应于李法场,M上的度量是[1]

度量Gα也被称作李度量或α-度量.关于这一课题的研究已有较大的进展[5-11].

命题 1[12]关于α-度量体积变分问题的Euler-Lagrange方程是

(1)

若一光滑严格凸函数f 满足式(1), 则我们称超曲面M={(x,f(x))}为α-相对极值超曲面. 相对于Calabi度量, 式(1)可写为

(2)

定理 1[13]设y:M→An+1是由严格凸函数xn+1=f(x1,x2,…,xn)给出的局部强凸α-相对极值超曲面, 且关于α度量完备,则存在正常数K(n). 当 |α|>K(n)时,M是椭圆抛物面.

本文研究满足下面四阶偏微分方程的超曲面

(3)

式中：h:R+→R.

注记定理2是定理1的推广.

2预备知识

设f(x1,…,xn)是定义在凸域Ω⊂An上的局部严格凸函数, 考虑超曲面

对M选取古典相对法场Y=(0,0,…,1). 则Calabi度量G=∑fijdxidxj是相对于Y的相对度量. 对位置向量y=(x1,…,xn, f(x1,…,xn))有

(4)

余法场

张量Aijk和Weingarten张量Bij满足

相应于度量G的联络有Chistoffel 符号

积分条件和Codazzi方程是

(8)

(9)

由式(8)得Ricci张量

(10)

定义函数

关于Calabi度量G的拉普拉斯算子

由Gα=ραG, 对光滑函数H有

(11)

式中： △和 △α分别是相对于Calabi度量G及α-度量Gα的拉普拉斯算子.

为了证明主要定理, 我们需先证明Φ=0, 再利用J-C-P定理来证.

3定理的证明

命题 2设f(x)是一局部严格凸函数, 且满足式(3), 则有

当Φ(p)=0时, 易得在点p处有

当Φ(p)≠0时, 取相对于Calabi度量的正交标架场使得在点p处有ρ,1=‖ρ‖G>0,ρ,i=0, ∀i>1. 因此有

(12)

利用Schwarz’s 不等式可得

由Ricci恒等式得

将上述关系式代入式(12)得

同理可得

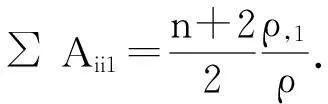
利用 Schwarz’s 不等式得

因此有

由

得

(13)

(14)

将式(13)及式(14)代入△Φ的关系式得

两边同时除以Φ, 得到命题 2.

定理 2 的证明设p0∈M, 令r=r(p0,p)为关于相对度量Gα的测地距离函数.a为任意正数, 设Ba(p0)={p∈M|r(p0,p)≤a}. 考虑定义在Ba(p0)上的函数

函数L在某内点p*处达到极大值. 设r2是p*某邻域内的C2-函数， 且在p*处Φ>0, 则在p*处有

直接计算得

(15)

由命题2及式(15)得

其中

由h满足

则可得

利用 Schwarz’s 不等式得

(16)

(17)

因此有

(18)

则有

(19)

式中：d2,d3是与n,α有关的常数. 注意到

(20)

及(M,Gα) 的α-Ricci曲率有下界-N. 由Laplacian 比较定理得

因此有

将此不等式及式(20)代入式(19)得

(21)

两边同除以(a2-r2)2, 得

(22)

式中：d4,d5是与n,N有关的常数. 式(21)在Ba(p0)上恒成立. ∀p∈M, 令a→∞得Φ(p)=0. 因此在M上有

利用J-C-P定理[15],M是椭圆抛物面. 证毕.

参考文献:

[1]Xu Ruiwei. Bernstein properties for some relative parabolic affine hyperspheres[J]. Result Math, 2008, 52： 409-422.

[2]Wu Yadong, Zhao Guosong. Hypersurfaces with Li-normalization and prescribed Gauss-kronecker curvature[J]. Result Math, 2011, 595： 63-576.

[3]Xiong Ming, Yang Baoying. Hyperbolic relative hyperspheres with Li-normalization[J]. Result Math, 2011, 595： 45-562.

[4]Wang Baofu, Xu Ruiwei. The euclidean complete affine hypersurfaces with negative relative constant affine mean curvature[J]. Journal of Sichuan University, 2008, 45： 1001-1006.

[5]Chen Bohui, Li Anming, Li Sheng. The Abreu equation with degenerated boundary conditions[J]. J.Differential Equation, 2012, 252： 5235-5259.

[6]Chen Bohui, Han Qing, Li Anming, Li Sheng. Interior estimates for the n-dimensional Abreu’s equation[J]. Advances in Mathematics, 2014, 251： 35-46.

[7]Li Anming, Xu Ruiwei. A rigidity theorem for an affine Kähler-Ricci flat graph[J]. Result Math, 2009, 56： 141-164.

[8]Wu Yadong. Asymptotic behaviors of hyperbolic hypersurfaces with constant affine Gauss-kronecker curvature[J]. Result Math, 2011, 59： 173-183.

[9]Wang Baofu. The affine complete hypersurfaces with constant Gauss-kronecker curvature[J]. Acta Mathematica Sinica, English Series, 2009, 25： 1353-1362.

[10]Li Anming, Jia Fang. A bernstein property of some fourth order partial differential equations[J]. Result Math, 2009, 56： 109-139.

[11]Li Anming, Jia Fang. A cubic from differential inequality with applications to affine Kähler-Ricci flat manifolds[J]. Result Math, 2009, 54： 329-340.

[12]Xu Ruiwei, Li Anming, Li Xingxiao. Euclidean completeαrelative extremal hypersurfaces[J]. Journal of Sichuan University, 2009, 46： 548-552.

[13]Xu, Ruiwei, Xiong Min, Li Sheng. Bernstein theorems for completeα- relative extremal hypersurfaces[J]. Ann Glob Anal Geom, 2013, 43： 143-152.

[14]Pogorelov A V. The Minkowski multidimensional problem[M]. John Wiley and Sons, 1978.

[15]Calabi E. Improper affine hyperspheres of convex type and a generalization of a theorem by K. Jörgens[J]. Michigan Math J., 1958, 55： 105-126.

Bernstein Property for Solutions of a Partial Differential Equation

HU Chuan-feng, JI Xiu

(School of Arts and Science, Yangtze University College, Jingzhou 434000, China)

Key words:Bernstein property; relative extremal hypersurface; partial differential equation; Euler-Lagrange equation

Abstract:Aα-relative metricGαwas defined on a locally strongly convex hypersurfaceM. LetMbe complete with respect toGαand itsα-Ricci curvature was bounded from below by a constant-N. By moving frames and J-C-P theorem, it drawed that the conclusion thatMmust be an elliptic paraboloid, whenρsatisfied a fourth order partial differential equation.

文章编号:1673-3193(2016)03-0220-05

收稿日期:2015-12-10

基金项目：湖北省教育厅科学技术研究基金资助项目(B2016458)

作者简介：胡传峰(1978-)， 男， 讲师， 硕士， 主要从事微分几何研究.

中图分类号:O186.13

文献标识码:A

doi:10.3969/j.issn.1673-3193.2016.03.003