生产函数框架下的中国能源及碳排放分解

朱文超　方兆本　吴遵

摘要：在生产函数框架下，本文将多维校准分解方法和完全结构分解方法结合，首先计算了2002～2007年各类能源使用的价格替代效应和实际技术进步，随后对期间中国碳排放增量进行了分解。本文发现，在观察期内能源之间的要素替代表现为电力替代煤炭和石油，石油是主要的被替代类能源。2002～2007年经济规模增长和资本强度提高是中国碳排放增长的主要因素，而能源使用实际技术进步则是帮助减少碳排放的主要因素，同时，劳动力的实际技术进步和价格替代效应、能源的价格替代效应、以及终端需求结构的变化，都对碳排放增长起到了抑制作用。

关键词：能源使用；碳排放；要素替代；技术进步

中图分类号：F062.2文献标识码：A文章编号：10035192（2015）02007105doi：10.11847/fj.34.2.71

1引言

在“十二五规划”中，中国政府提出了新的节能减排目标。而这些目标需要一系列政策的共同实施来实现，如投资可再生能源、推广节能技术、产业结构转变和要素替代等。为最大程度发挥各政策效应，有必要知道影响中国能源消耗和碳排放增长的因素，这些因素又在过去产生了何种影响。之前文献一般采用结构分解法（Structural Decomposition Analysis， SDA）和指数分解法（Index Decomposition Analysis， IDA），对中国能源和碳排放总量或强度展开分解，考察分解后的各影响因素产生何种作用，从而提出相关政策建议，采用SDA方法的如，Chang和Lin[1]，Chang等[2]和郭朝先[3]，采用IDA方法的如，Zhang等[4]，陈诗一[5]。虽然上述文献取得了丰硕成果，但由于SDA和IDA建立在单能源投入单产出框架基础上，投入要素只有能源，是基本的三因素分解模型，无法考察非能源要素投入技术进步对能源消耗和碳排放增长的影响，更无法考察价格激励引起的要素替代的影响。因此，采用SDA和IDA方法得到的结果，指导考虑非能源要素投入技术进步和要素替代等更全面政策组合的时候，存在一定局限性。在这种情况下，更适合的是建立在生产函数框架下考虑多要素投入的分解模型，而Okushima和Tamura[6]基于不变替代效应生产函数提出的多维校准分解方法（Multiple Calibration Decomposition Analysis， MCDA）提供了一种全新思路。MCDA基本思想是基期各投入要素在一均衡状态下进行生产，在下一期伴随要素价格波动和技术进步达到了新均衡状态，通过两个均衡状态比较，将投入要素强度变化分解为价格替代效应和实际技术进步，Okushima和Tamura[6，7]首先使用MCDA对日本的能源使用进行了分解，并认为MCDA具有效率高、易理解和数据要求低的优点。MCDA不仅可以考察能源之间的要素替代，而且可以考察能源与非能源要素之间的要素替代，因此，MCDA作为一种多要素分解技术，解决了如何考察要素替代和非能源要素投入技术进步的问题，随后，可结合完全SDA分解方法[8，9]，在生产函数框架下进行全要素分解，从而克服了单要素框架下SDA和IDA方法无法考察要素替代和非能源要素投入技术进步影响的弱点。

因此，本文的目的即首先使用MCDA计算2002～2007年各类能源使用的价格替代效应和实际技术进步，随后结合基于生产函数框架的完全SDA方法，对2002～2007年中国碳排放增量展开分解。相比其它文献本文特色在于：第一，本文采用的分解方法基于生产函数框架，可以计算非能源投入要素技术进步对能源消耗和碳排放增长的影响；第二，通过分解计算的价格替代效应可以分析各行业回应市场各类能源价格变化的差异；第三，补充之前文献缺少要素替代对中国能源消耗和碳排放增长影响的研究。在笔者可搜索的文献范围内，虽然有很多针对中国能源消耗和碳排放增长的因素分解的研究，但本文是第一次采用全要素（包括资本、劳动力和能源）分解的研究，因此，将得到更完全的结果，能为相关单位制定节能减排政策提供更全面的指导。

朱文超，等：生产函数框架下的中国能源及碳排放分解

Vol.34， No.2预测2015年第2期

2基于MCDA的能源使用分解

2.1MCDA方法

根据MCDA，行业j有3种投入要素，分别为劳动力（L）、资本（K）和能源（E），同时行业j在第t年的产出为Xj，依照能源强度定义，定义t年行业j各投入要素强度atFj，如下

atFj=XtFjXtj，F=L，K，E（1）

其中XtFj为行业j第t年各要素投入数量，Xtj为行业j第t年总产出，根据不变替代效应生产函数，有如下函数模型

atFj=λtFjβσ-1j（αFjptjptFj）σ（2）

其中投入要素强度atFj已知，参数λtFj为各投入要素的技术参数，β为规模系数，ptj为行业j产品在t年价格，ptFj为投入要素F在t年价格，σ为常数弹性替代系数，外生给定，αFj为各投入要素比例参数，满足∑αFj=1。基期第t年各投入要素的技术参数λ设为1，ptj和ptFj数据均来自历年各价格指数，在t年也都被标准化为1。从而可求出第t年的规模系数β和各投入要素比例参数αFj，另外，这里假定以后年份的β和αFj都保持不变（这种处理过程也可见于文献[10]）。

在MCDA中，要素E包含了煤炭、石油、天然气和电力等不同能源种类，为了更进一步研究不同能源种类之间的价格替代效应，设有n种能源，同（2）式定义如下函数

bteij=etijEtj=λteijβσe-1ej（αeijptEptei）σe，i=1， 2， …， n（3）

其中i表示第i种能源，etij和Etj分别为行业j第t年消耗能源i的数量和能源消耗总量，故bteij为第i种能源占总能源比重，（3）式的λ和β也分别为各类能源的技术参数和规模系数，λ为1，比例参数满足∑αeij=1。ptE为第t年总能源要素价格，ptei为t年第i种能源价格，在第t年都被标准化为1。σe为各类能源的常数弹性替代系数，也外生给定。从而可求得第t年（3）式中的规模系数β和比例参数αeij，同样，假定以后年份的β和αeij保持不变。从而可获得如下第t年各类能源投入的不变替代效应生产函数等式

ateij=XtEjXtjetijXtEj=λtEjβσ-1j（αEjptjptEj）σ·

λteijβσe-1ej（αeijptEptei）σe（4）

同（2）式和（4）式，可写出第t+1年各类投入要素的不变替代效应生产函数等式

at+1Fj=Xt+1FjXt+1j=λt+1Fjβσ-1j（αFjpt+1jpt+1Fj）σ，F=L，K，E

at+1eij=Xt+1EjXt+1jet+1ijXt+1Ej=λt+1Ejβσ-1j（αEjpt+1jpt+1E）σ·

λt+1eijβσe-1ej（αeijpt+1Ept+1ei）σe（5）

由于第t+1年各类投入要素强度和各要素价格已知，规模系数和比例参数可从（2）式和（4）式求得，弹性替代系数给定，从而可求得各λt+1Fj和λt+1Ej。从（5）式看出，各投入要素强度相比基期的变化主要取决于价格和技术参数的变化，即投入要素强度是价格p和技术参数λ的函数，可表示如下

aFj=f（λ，p）（6）

对t+1年和t年之间的投入要素强度变化可再进行如下分解

at+1Fj-atFj=[f（λt+1，pt+1）-f（λt，pt+1）]+

[f（λt，pt+1）-f（λt，pt）]（7）

从而（7）式也可写为如下形式

ΔaFj=FIC=TC+PS（8）

其中f（λt，pt+1）表示使用第t年技术第t+1年价格计算的投入要素强度，故（7）式右边第一个中括号表示在相同价格情况下技术变化引起的投入要素强度变化，即（8）式中的TC，第二个中括号则表示在同技术情况下价格变化引起的投入要素强度变化，即（8）式中的PS，（8）式中的FIC表示各类投入要素强度总的变化。通过（7）式即可将各投入要素强度变化分解为价格替代效应PS和实际技术进步TC。f（λt，pt+1）可通过下式求得

f（λt，pt+1）=λtFjβσ-1j（αFjpt+1jpt+1Fj），F=L，K，E

λtEjβσ-1j（αEjpt+1jpt+1E）σ×λteijβσe-1ej（αeijpt+1Ept+1ei）σe，

i=1，…，n（9）

2.2数据来源及结果分析

由于各行业出厂品价格指数始于2002年，而最新投入产出表为2007年，故只选择了2002～2007年作为本文研究时间段。各行业投入产出数据来自2002和2007年两个投入产出表，参照投入产出表，本文共分25个行业进行计算。选取各行业出厂品价格指数作为各行业产品价格，2002年价格都被标准化为1，数据来自历年《中国物价统计年鉴》。各行业能源消耗数据来自历年《中国能源统计年鉴》，共分三种能源，分别为煤炭、石油和电力，天然气则按GB/T 25892008上的转换系数被归到石油，并分别选取煤炭开采业、石油天然气开采业和电力工业出厂品价格指数作为这三类能源的价格，总能源价格指数根据这三类能源所占比例加权计算获得。各行业劳动力人数选自历年《中国统计年鉴》，选取各行业工资作为劳动力价格，并将2002年工资标准化为1。资本选取的是各行业固定资产投资数据，同样来自历年《中国统计年鉴》。资本价格则选自中国人民银行1至3年期贷款利率，来自国泰安金融数据库。相关数据都使用了CPI指数平减为2002年价格。参考Okushima和Tamura[6]，本文选取σ=0.1，σe=1。

根据MCDA，本文将2002～2007年中国各类能源投入强度（FIC），分解成实际技术进步（TC）和价格替代效应（PS）两部分。对煤炭的分解结果显示，2002～2007年除金属开采、煤炭开采、石油开采、石油加工业和造纸印刷业外，其余行业的煤炭TC和PS都为负，负的TC表明在观察期内，大多数行业的煤炭使用技术都实现了稳定提高，但由于负的价格替代效应存在，其实际技术进步要差于用FIC表示的技术进步，如通信设备和计算机制造业，FIC表示的技术进步显示2007年比2002年煤炭强度下降25.75%，但由价格替代效应帮助下降了7.63%，导致实际的技术进步只帮助下降18.12%。而对金属开采、煤炭开采、石油开采和石油加工业，它们的煤炭价格替代效应都为正，可以发现它们多为能源工业和原材料供应业，位于整个经济系统上游，这部分行业由于它们行业位置优势，可以很容易将提高的能源成本转嫁到下游行业，其结果表现是这些行业对煤炭价格上涨并不敏感，伴随各投入要素价格上涨，这些行业会选用煤炭作为替代投入要素。另外，2002～2007年，煤炭TC和FIC同时为正的仅有煤炭开采业和造纸印刷业，表明这两个行业在观察时间段内，并没有很好地实现集约式发展，带来煤炭使用技术进步，相反存在继续地粗放式发展。

对石油的分解结果显示2002～2007年所有行业的PS都为负，除交通运输业以外的FIC都为负，而实际技术进步TC除农业、金属制品业、建筑业和交通运输业为正外，其余行业都为负。特别是农业、金属制品业和建筑业，如果使用石油投入强度变化FIC看，这3个行业的石油使用技术都表现出了显著的技术进步，但在考虑价格替代效应后，发现实际技术进步出现了倒退。对农业本文认为这与近年我国逐步使用机械化生产替代人力生产，而机械化生产需要消耗大量的汽柴油有关。而建筑业则由于我国近年持续的城镇化建设和高投资需求，带来大量的建材运输需求，而这同样需要消耗大量的汽柴油。另外，值得注意的是交通运输业，除了PS为负以外，FIC和TC都为正，交通运输业表现出旺盛的汽柴油需求，正如Zhang等[4]所述，随着消费者收入增长，会追求更加舒适的出行方式，而导致交通运输业实际技术进步表现为退步。再计算能源工业和非能源开采业的平均石油PS为-16%，而剩余行业的平均石油PS为-19%，该结果与煤炭类似，位于整个经济系统上游的行业表现出比下游行业更低的石油价格敏感度。

最后电力的分解结果显示所有行业电力PS都为正，表明都选择使用电力替代其它类能源要素投入，电力FIC有正有负，因存在正电力价格替代效应，实际电力使用技术进步要好于用电力投入强度表示的技术进步，所有行业的电力TC都为负，出现了显著的技术进步。

3中国CO2排放分解

3.1完全SDA方法

接下来，本文将使用第二部分的结果结合完全SDA方法，对中国CO2排放展开分解。完全SDA在生产函数框架下，将能源消耗或碳排放增长分为两部分，一部分由终端需求变化引起，另一部分由投入系数矩阵的变化引起。投入系数矩阵变化的分解由于包含了资本、劳动力和能源投入要素，又称为KLE效应[9，11]。下文的分解过程主要参照了Casler 和Rose[9]。

设c为各行业各类能源CO2排放强度矩阵，根据投入产出表，CO2排放总量可表示如下

ΠTOT=c（I-A）-1Y（10）

其中I和A分别为单位矩阵和投入要素强度矩阵，（I-A）-1即为Leontief逆矩阵，再令（10）式中的c（I-A）-1=Π，Π即为一碳排放强度矩阵，Y为终端需求矩阵。从而，一段时间内的总碳排放变化可表示如下

ΔΠTOT=Δc（I-A）-1Y+c（I-A）-1ΔY+ε（11）

即（11）式首先把总碳排放变化主要分解成两部分：碳排放强度矩阵和终端需求矩阵的变化引起的变化。ε为交互作用项，ε=Δc（I-A）-1ΔY。再令（11）式右边第一项Δc（I-A）-1Y=ΔΠTOT，KLE，而Δc（I-A）-1=ΔΠ。根据Casler和Rose[9]，Rose[12]的推导，ΔΠ≌ΠtΔAΠt，从而可得下式

ΔΠTOT，KLE≌（ΠtΔAΠt）Y（12）

其中ΔA为投入强度矩阵变化，根据Rose和Chen[8]，ΔA可进一步进行KLE效应分解，分解为各投入要素的价格替代效应和实际技术进步之和，如下

ΔA=ΔATCK+ΔAPSK+ΔATCL+ΔAPSL+ΔATCE+ΔAPSE（13）

其中右上标TC表示由实际技术变化引起的要素强度变化，PS表示由价格替代效应引起的要素强度变化，再将（13）式代入（12）式，可得

ΔΠTOT，KLE≌ΠtΔATCKΠtY+ΠtΔAPSKΠtY+ΠtΔATCLΠtY+

ΠtΔAPSLΠtY+ΠtΔATCEΠtY+ΠtΔAPSEΠtY（14）

即（14）式将（11）式右边第一项分解成6项，分别由资本、劳动力和能源的实际技术进步和价格替代效应引起。（11）式右边第二项由终端需求变化引起，终端需求变化ΔY可进一步进行如下分解

ΔY=Yt+1-Yt

=（Yt+1-Yt+1ΣiYitΣiYit+1）+（Yt+1ΣiYitΣiYit+1-Yt）（15）

其中Yt+1ΣiYitΣiYit+1将第t+1年的终端消费平减为第t年规模，因此，（15）式右边第一个括号测度了在第t+1年到第t年时间段内，终端需求是否随经济规模进行了同样比例的增长，称为纯经济增长效应。（15）式右边第二个括号测度了在时间段内终端需求结构变化引起的变化，称为混合效应。再将（15）式代入（11）式右边第二项，可得

c（I-A）-1ΔY=c（I-A）-1（Yt+1-Yt+1ΣiYitΣiYit+1）+c（I-A）-1（Yt+1ΣiYitΣiYit+1-Yt）（16）

从而，（16）式结合（14）式完成了对（11）式中国碳排放增长的分解。

3.2结果分析

2基于MCDA的能源使用分解

2.1MCDA方法

根据MCDA，行业j有3种投入要素，分别为劳动力（L）、资本（K）和能源（E），同时行业j在第t年的产出为Xj，依照能源强度定义，定义t年行业j各投入要素强度atFj，如下

atFj=XtFjXtj，F=L，K，E（1）

其中XtFj为行业j第t年各要素投入数量，Xtj为行业j第t年总产出，根据不变替代效应生产函数，有如下函数模型

atFj=λtFjβσ-1j（αFjptjptFj）σ（2）

其中投入要素强度atFj已知，参数λtFj为各投入要素的技术参数，β为规模系数，ptj为行业j产品在t年价格，ptFj为投入要素F在t年价格，σ为常数弹性替代系数，外生给定，αFj为各投入要素比例参数，满足∑αFj=1。基期第t年各投入要素的技术参数λ设为1，ptj和ptFj数据均来自历年各价格指数，在t年也都被标准化为1。从而可求出第t年的规模系数β和各投入要素比例参数αFj，另外，这里假定以后年份的β和αFj都保持不变（这种处理过程也可见于文献[10]）。

在MCDA中，要素E包含了煤炭、石油、天然气和电力等不同能源种类，为了更进一步研究不同能源种类之间的价格替代效应，设有n种能源，同（2）式定义如下函数

bteij=etijEtj=λteijβσe-1ej（αeijptEptei）σe，i=1， 2， …， n（3）

其中i表示第i种能源，etij和Etj分别为行业j第t年消耗能源i的数量和能源消耗总量，故bteij为第i种能源占总能源比重，（3）式的λ和β也分别为各类能源的技术参数和规模系数，λ为1，比例参数满足∑αeij=1。ptE为第t年总能源要素价格，ptei为t年第i种能源价格，在第t年都被标准化为1。σe为各类能源的常数弹性替代系数，也外生给定。从而可求得第t年（3）式中的规模系数β和比例参数αeij，同样，假定以后年份的β和αeij保持不变。从而可获得如下第t年各类能源投入的不变替代效应生产函数等式

ateij=XtEjXtjetijXtEj=λtEjβσ-1j（αEjptjptEj）σ·

λteijβσe-1ej（αeijptEptei）σe（4）

同（2）式和（4）式，可写出第t+1年各类投入要素的不变替代效应生产函数等式

at+1Fj=Xt+1FjXt+1j=λt+1Fjβσ-1j（αFjpt+1jpt+1Fj）σ，F=L，K，E

at+1eij=Xt+1EjXt+1jet+1ijXt+1Ej=λt+1Ejβσ-1j（αEjpt+1jpt+1E）σ·

λt+1eijβσe-1ej（αeijpt+1Ept+1ei）σe（5）

由于第t+1年各类投入要素强度和各要素价格已知，规模系数和比例参数可从（2）式和（4）式求得，弹性替代系数给定，从而可求得各λt+1Fj和λt+1Ej。从（5）式看出，各投入要素强度相比基期的变化主要取决于价格和技术参数的变化，即投入要素强度是价格p和技术参数λ的函数，可表示如下

aFj=f（λ，p）（6）

对t+1年和t年之间的投入要素强度变化可再进行如下分解

at+1Fj-atFj=[f（λt+1，pt+1）-f（λt，pt+1）]+

[f（λt，pt+1）-f（λt，pt）]（7）

从而（7）式也可写为如下形式

ΔaFj=FIC=TC+PS（8）

其中f（λt，pt+1）表示使用第t年技术第t+1年价格计算的投入要素强度，故（7）式右边第一个中括号表示在相同价格情况下技术变化引起的投入要素强度变化，即（8）式中的TC，第二个中括号则表示在同技术情况下价格变化引起的投入要素强度变化，即（8）式中的PS，（8）式中的FIC表示各类投入要素强度总的变化。通过（7）式即可将各投入要素强度变化分解为价格替代效应PS和实际技术进步TC。f（λt，pt+1）可通过下式求得

f（λt，pt+1）=λtFjβσ-1j（αFjpt+1jpt+1Fj），F=L，K，E

λtEjβσ-1j（αEjpt+1jpt+1E）σ×λteijβσe-1ej（αeijpt+1Ept+1ei）σe，

i=1，…，n（9）

2.2数据来源及结果分析

由于各行业出厂品价格指数始于2002年，而最新投入产出表为2007年，故只选择了2002～2007年作为本文研究时间段。各行业投入产出数据来自2002和2007年两个投入产出表，参照投入产出表，本文共分25个行业进行计算。选取各行业出厂品价格指数作为各行业产品价格，2002年价格都被标准化为1，数据来自历年《中国物价统计年鉴》。各行业能源消耗数据来自历年《中国能源统计年鉴》，共分三种能源，分别为煤炭、石油和电力，天然气则按GB/T 25892008上的转换系数被归到石油，并分别选取煤炭开采业、石油天然气开采业和电力工业出厂品价格指数作为这三类能源的价格，总能源价格指数根据这三类能源所占比例加权计算获得。各行业劳动力人数选自历年《中国统计年鉴》，选取各行业工资作为劳动力价格，并将2002年工资标准化为1。资本选取的是各行业固定资产投资数据，同样来自历年《中国统计年鉴》。资本价格则选自中国人民银行1至3年期贷款利率，来自国泰安金融数据库。相关数据都使用了CPI指数平减为2002年价格。参考Okushima和Tamura[6]，本文选取σ=0.1，σe=1。

根据MCDA，本文将2002～2007年中国各类能源投入强度（FIC），分解成实际技术进步（TC）和价格替代效应（PS）两部分。对煤炭的分解结果显示，2002～2007年除金属开采、煤炭开采、石油开采、石油加工业和造纸印刷业外，其余行业的煤炭TC和PS都为负，负的TC表明在观察期内，大多数行业的煤炭使用技术都实现了稳定提高，但由于负的价格替代效应存在，其实际技术进步要差于用FIC表示的技术进步，如通信设备和计算机制造业，FIC表示的技术进步显示2007年比2002年煤炭强度下降25.75%，但由价格替代效应帮助下降了7.63%，导致实际的技术进步只帮助下降18.12%。而对金属开采、煤炭开采、石油开采和石油加工业，它们的煤炭价格替代效应都为正，可以发现它们多为能源工业和原材料供应业，位于整个经济系统上游，这部分行业由于它们行业位置优势，可以很容易将提高的能源成本转嫁到下游行业，其结果表现是这些行业对煤炭价格上涨并不敏感，伴随各投入要素价格上涨，这些行业会选用煤炭作为替代投入要素。另外，2002～2007年，煤炭TC和FIC同时为正的仅有煤炭开采业和造纸印刷业，表明这两个行业在观察时间段内，并没有很好地实现集约式发展，带来煤炭使用技术进步，相反存在继续地粗放式发展。

对石油的分解结果显示2002～2007年所有行业的PS都为负，除交通运输业以外的FIC都为负，而实际技术进步TC除农业、金属制品业、建筑业和交通运输业为正外，其余行业都为负。特别是农业、金属制品业和建筑业，如果使用石油投入强度变化FIC看，这3个行业的石油使用技术都表现出了显著的技术进步，但在考虑价格替代效应后，发现实际技术进步出现了倒退。对农业本文认为这与近年我国逐步使用机械化生产替代人力生产，而机械化生产需要消耗大量的汽柴油有关。而建筑业则由于我国近年持续的城镇化建设和高投资需求，带来大量的建材运输需求，而这同样需要消耗大量的汽柴油。另外，值得注意的是交通运输业，除了PS为负以外，FIC和TC都为正，交通运输业表现出旺盛的汽柴油需求，正如Zhang等[4]所述，随着消费者收入增长，会追求更加舒适的出行方式，而导致交通运输业实际技术进步表现为退步。再计算能源工业和非能源开采业的平均石油PS为-16%，而剩余行业的平均石油PS为-19%，该结果与煤炭类似，位于整个经济系统上游的行业表现出比下游行业更低的石油价格敏感度。

最后电力的分解结果显示所有行业电力PS都为正，表明都选择使用电力替代其它类能源要素投入，电力FIC有正有负，因存在正电力价格替代效应，实际电力使用技术进步要好于用电力投入强度表示的技术进步，所有行业的电力TC都为负，出现了显著的技术进步。

3中国CO2排放分解

3.1完全SDA方法

接下来，本文将使用第二部分的结果结合完全SDA方法，对中国CO2排放展开分解。完全SDA在生产函数框架下，将能源消耗或碳排放增长分为两部分，一部分由终端需求变化引起，另一部分由投入系数矩阵的变化引起。投入系数矩阵变化的分解由于包含了资本、劳动力和能源投入要素，又称为KLE效应[9，11]。下文的分解过程主要参照了Casler 和Rose[9]。

设c为各行业各类能源CO2排放强度矩阵，根据投入产出表，CO2排放总量可表示如下

ΠTOT=c（I-A）-1Y（10）

其中I和A分别为单位矩阵和投入要素强度矩阵，（I-A）-1即为Leontief逆矩阵，再令（10）式中的c（I-A）-1=Π，Π即为一碳排放强度矩阵，Y为终端需求矩阵。从而，一段时间内的总碳排放变化可表示如下

ΔΠTOT=Δc（I-A）-1Y+c（I-A）-1ΔY+ε（11）

即（11）式首先把总碳排放变化主要分解成两部分：碳排放强度矩阵和终端需求矩阵的变化引起的变化。ε为交互作用项，ε=Δc（I-A）-1ΔY。再令（11）式右边第一项Δc（I-A）-1Y=ΔΠTOT，KLE，而Δc（I-A）-1=ΔΠ。根据Casler和Rose[9]，Rose[12]的推导，ΔΠ≌ΠtΔAΠt，从而可得下式

ΔΠTOT，KLE≌（ΠtΔAΠt）Y（12）

其中ΔA为投入强度矩阵变化，根据Rose和Chen[8]，ΔA可进一步进行KLE效应分解，分解为各投入要素的价格替代效应和实际技术进步之和，如下

ΔA=ΔATCK+ΔAPSK+ΔATCL+ΔAPSL+ΔATCE+ΔAPSE（13）

其中右上标TC表示由实际技术变化引起的要素强度变化，PS表示由价格替代效应引起的要素强度变化，再将（13）式代入（12）式，可得

ΔΠTOT，KLE≌ΠtΔATCKΠtY+ΠtΔAPSKΠtY+ΠtΔATCLΠtY+

ΠtΔAPSLΠtY+ΠtΔATCEΠtY+ΠtΔAPSEΠtY（14）

即（14）式将（11）式右边第一项分解成6项，分别由资本、劳动力和能源的实际技术进步和价格替代效应引起。（11）式右边第二项由终端需求变化引起，终端需求变化ΔY可进一步进行如下分解

ΔY=Yt+1-Yt

=（Yt+1-Yt+1ΣiYitΣiYit+1）+（Yt+1ΣiYitΣiYit+1-Yt）（15）

其中Yt+1ΣiYitΣiYit+1将第t+1年的终端消费平减为第t年规模，因此，（15）式右边第一个括号测度了在第t+1年到第t年时间段内，终端需求是否随经济规模进行了同样比例的增长，称为纯经济增长效应。（15）式右边第二个括号测度了在时间段内终端需求结构变化引起的变化，称为混合效应。再将（15）式代入（11）式右边第二项，可得

c（I-A）-1ΔY=c（I-A）-1（Yt+1-Yt+1ΣiYitΣiYit+1）+c（I-A）-1（Yt+1ΣiYitΣiYit+1-Yt）（16）

从而，（16）式结合（14）式完成了对（11）式中国碳排放增长的分解。

3.2结果分析

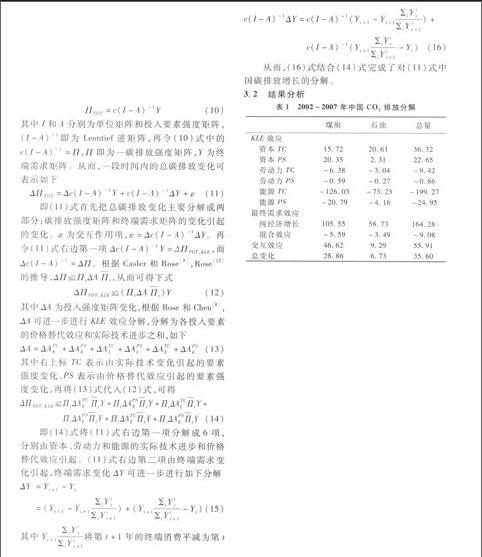
这里首先使用《1995年政府间气候变化委员会（IPCC）温室气体清单指南》提供的不同能源转换系数，计算了中国CO2排放总量，结果显示2007年比2002年增加CO2排放35.6亿吨。随后使用上文的完全SDA分解方法对2002～2007年中国CO2排放增量进行了分解，具体结果见表1。从表1看出，2002～2007年对中国CO2排放增加贡献最大的来自终端需求的纯经济增长效应，达164.28亿吨，这与Zhang等[4]，郭朝先[3]结果一致，经济扩张效应是中国CO2排放增加的主要因素。同时，发现终端需求的混合效应为负，而混合效应反映了终端需求行业结构的变化，意味着由于终端消费部门对不同行业消费偏好的变化，帮助减少了CO2排放9.08亿吨。比较2002和2007年终端消费部门的行业需求结构，发现负的混合效应主要原因是对日常消费品（包括农副食品加工业、电气制造业和计算机通讯设备制造业）需求上升，而对原材料供应行业（包括煤炭开采业、石油天然气开采业和非金属矿开采业）需求下降引起。KLE效应中只有资本的TC和PS都为正，PS为正反映了资本相对其它投入要素较低的成本，TC也为正则反映了中国经济中不断提高的资本强度，这进一步意味着高资本强度行业在中国经济体中占比的提高，而高资本强度行业往往属于能源密集型行业，会对节能减排起到负的影响，这可以从王兵等[13]人均资本上升对中国全要素能源效率起到负的影响得到证实。劳动力的TC为负，显然说明了由于近年劳动力素质的提高，提高了生产效率，对中国CO2排放减少起到了促进作用。而劳动力的PS也为负，表明随着各行业工资上涨，劳动力成本的提高，会采用如资本等其它要素替代劳动力，从而帮助减少CO2排放。能源的TC为负，且在所有因素中对减少CO2排放贡献最大，达199.27亿吨。同时，伴随能源价格上涨，石油和煤炭的能源价格替代效应帮助中国2002～2007年减少CO2排放24.95亿吨，表明使用价格杠杆，有效激励能源效率提高，将进一步帮助减少CO2排放。

总的来看，虽然KLE效应中劳动力和能源的价格替代效应都为负，但来自资本的正价格替代效应抵消较大，致使净价格替代效应只帮助中国2002～2007年减少CO2排放3.16亿吨，另外，终端需求的结构变化，也只帮助减少碳排放9.08亿吨，而各投入要素的技术进步帮助减少碳排放达172.37亿吨，意味着未来中国依然主要应该依靠技术进步，特别是能源使用技术进步来实现自身的节能减排目标。

4结论

在生产函数框架下，本文首先使用MCDA方法将2002～2007年各类能源强度分解为价格替代效应和实际技术进步，随后结合完全SDA分解方法对2002～2007年中国碳排放增长进行了分解，主要结论如下：

（1）对煤炭，处于经济系统上游的能源工业和原材料供应业对煤炭价格上涨并不敏感，表现为煤炭投入替代其它类能源投入，在观察期内，除煤炭开采和造纸印刷业外，其余行业实际煤炭使用技术都出现了显著进步。对石油，观察期内较快的石油价格增长，导致各行业都表现为其它类能源投入替代石油投入，石油使用实际技术进步显著差于用石油强度表示的技术进步，特别是农业、建筑业和交通运输业对石油产品需求的大幅增加，导致实际技术进步出现了恶化。对电力，在观察期内各行业都表现为正的价格替代效应，选择电力替代其它类能源投入，实际电力使用技术进步好于用电力强度表示的技术进步。

（2）2002～2007年经济规模增长是对中国CO2排放增加贡献最大的因素，另外，本文新发现资本强度的提高也会对碳排放增长起到显著促进作用；能源使用实际技术进步则是对减少碳排放贡献最大的因素，但由于负的能源价格替代效应存在，能源使用技术进步的贡献并没有预期那么大，而来自劳动力的实际技术进步和价格替代效应，以及终端需求结构的变化，也都对CO2排放增长起到了负的作用。总的来看，净价格替代效应和终端需求结构转变帮助中国减少碳排放量仅占实际技术进步的7.1%，未来中国节能减排目标主要应该依靠技术进步，特别是能源使用技术进步来实现。

至此，本文提出如下有别于其它文献的政策建议：

第一，位于经济系统上游的能源工业和原材料供应业，由于其位置优势，相对其它行业对能源价格上涨敏感度低，要求能源价格的定价机制应偏向保护终端消费者，促使它们首先考虑内部消化投入成本提高，提高价格杠杆对它们的激励作用。

第二，资本强度的提高会显著增加中国CO2排放，而资本密集行业多为高能耗高碳排放行业，要求相关单位控制对资本密集行业投资规模，引导资金投向节能减排项目。

参考文献：

[1]Chang Y F， Lin S J. Structural decomposition of industrial CO2 emission in Taiwan： an inputoutput approach[J]. Energy Policy， 1998， 26（1）： 512.

[2]Chang Y F， Charles L， Lin S J. Comprehensive evaluation of industrial CO2 emission（19892004）in Taiwan by inputoutput structural decomposition[J]. Energy Policy， 2008， 36（7）： 24712480.

[3]郭朝先.中国二氧化碳排放增长因素分析——基于SDA分解技术[J].中国工业经济，2010，（12）：4756.

[4] Zhang M， Mu H L， Ning Y D， et al.. Accounting for energyrelated CO2 emission in China， 19912006[J]. Energy Policy， 2009， 37（3）： 767773.

[5]陈诗一.中国碳排放强度的波动下降模式及经济学解释[J].世界经济，2011，（4）：124143.

[6]Okushima S， Tamura M. Multiple calibration decomposition analysis： energy use and carbon dioxide emissions in the Japanese economy， 19701995[J]. Energy Policy， 2007， 35（10）： 51565170.

[7]Okushima S， Tamura M. What causes the change in energy demand in the economy？ The role of technological change[J]. Energy Economics， 2010， 32（1）： 4146.

[8]Rose A， Chen C Y. Sources of change in energy use in the US economy， 19721982： a structural decomposition analysis[J]. Resources and Energy， 1991， 13（1）： 121.

[9]Casler S， Rose A. Carbon dioxide emissions in the US economy： a structural decomposition analysis[J]. Environmental and Resource Economics， 1998， 11（3）： 349363.

[10]Shoven J B， Whalley J. Applied generalequilibrium models of taxation and international trade： an introduction and survey[J]. Journal of Economic Literature， 1984， 22（3）： 10071051.

[11]Hudson E， Jorgenson D. U S energy policy and economic growth， 19752000[J]. Bell Journal of Economics， 1974， 5（2）： 1125.

[12]Rose A. Handbook of environmental and resource economics[M]. Cheltenham： Edward Elgar Press， 1999. 11641179.

[13]王兵，张技辉，张华.环境约束下中国省际全要素能源效率实证分析[J].经济评论，2011，（4）：3143.