下视影像辅助大倾斜影像外方位角元素的解算

柯　玲，范冬娟，徐　彬

（1.武昌首义学院基础科学部，武汉 430064；2.武汉大学遥感信息工程学院，武汉 430079；3.73608部队，南京 210028）



下视影像辅助大倾斜影像外方位角元素的解算

柯玲1，2，范冬娟3，徐彬1

（1.武昌首义学院基础科学部，武汉 430064；2.武汉大学遥感信息工程学院，武汉 430079；3.73608部队，南京 210028）

摘要：本文在已有研究成果基础上，采用下视和倾斜同步摄影方式获取多视影像，改进了传统摄影方式，并在下视影像辅助下实现了无控制条件下大倾斜影像的外方位角元素解算。

关键词：大倾斜影像；下视影像；POS；外方位元素；无控制

范冬娟，女，1976年生，湖北天门人，硕士，高级工程师，主要研究方向是数字摄影测量、GIS。

徐 彬，女，1981年生，山东昌邑人，硕士，讲师，主要研究方向是应用数学方面的研究。

1 引言

相比传统的竖直摄影方式，倾斜摄影获取的影像更加接近一般的地面投影，其结果也更符合人们的日常感受，正受到越来越多的关注。倾斜摄影目前主要分为两种形式：一是采用较低倾斜角度，以获取飞行器侧下方影像为主的倾斜摄影方式；另一种则是采用较大倾斜角度，以获取飞行器侧面至地平线远处影像为主要目的倾斜摄影方式。相对于多镜头的低倾斜角度摄影，利用单个相机进行大倾角摄影的主要目的是用于军事侦察或危机地域实时信息获取，因其倾角较大且没有类似多镜头相机那样的几何约束关系，尽管其影像获取简单，但地理参考更加复杂，难以进行自动匹配或常规摄影测量处理［3］。

2 外方位元素解算流程与方法

当前，集DGPS（Differential GPS）技术和惯性导航（Inertial Navigation System）技术于一体的POS系统已广泛应用于无人机等低空遥感摄影系统，在近似水平摄影且摄影比例尺较大的情况下（大于1︰10万比例尺），采用机载POS进行直接的地理定位已可以满足1︰5万正射影像图制作精度要求［9］，获取的像片姿态角经过转换也可以作为外方位元素的初值使用，在这一基础上，研究下视影像辅助下大倾角影像外方位角元素的解算方法，实现了无控制条件下大倾斜影像外方位元素求解和地面坐标量测。其处理流程如图1所示。

图1　无控制条件下倾斜影像处理流程

当前在航摄作业过程中，一般都会随影像提供高精度的定位定向数据，也就是通常所说的POS （Position & Orientation System）数据，利用该数据可以实现对地面目标的直接地理定位，即直接对POS系统获取的GPS天线相位中心的空间坐标及IMU系统获取的侧滚角、俯仰角、航迹角进行数据处理，获取航空影像曝光瞬间的摄站坐标Xs, Ys, Zs及3个姿态角φ,ω,κ共6个外方位元素［10］，进而解算地面坐标。在6个外方位元素中，利用载波相位GPS动态定位技术，摄站位置的平面和高程精度可分别达到2cm和5cm，完全可以满足摄影测量的精度要求，而3个角元素的精度则受限于IMU精度的影响，难以直接作为影像的外方位元素使用，因此对外方位元素的求解问题就可以简化为求解3个角元素φ,ω,κ的问题。在摄影测量处理过程中，遥感影像的外方位元素获取依赖于地面控制点，通过建立地面控制点和其像点之间的共线关系来解算外方位元素，因此在无控制条件下如何建立这样的关系条件成为解算外方位元素的关键所在。

2.1 模拟控制点

在航摄过程中采用了竖直摄影和倾斜摄影相结合的方式，在获取倾斜影像的同时，获取竖直影像，如图2所示。

图2　竖直和倾斜同步摄影示意图

在图2中，O0为倾斜摄影相机的像主点，S0为其摄站点；O1为竖直摄影相机的像主点，S1为其摄站点，N点是竖直摄影相机摄站点和像主点的连线与地面的交点，也就是O1对应的地面点；n为N在倾斜影像上的对应像点，可知，n是O1的同名像点。对于竖直航摄影像来说，摄站点经像主点投射线竖直向下，此时可以根据式（1）得到像主点对应的地面点坐标。

式中，（X,Y,Z）为N点坐标；Xs，Ys，Zs为摄站坐标；H为航高，考虑到航高存在的误差以及地面起伏的影响，可采用DEM内插的方式获得N点Z坐标。在求得N点坐标后，可将N点作为控制点，再进一步得到n点的像点坐标，即可建立S0，n，N三点共线的数学方程。根据航摄过程中的航线重叠和旁向重叠情况，在一张倾斜影像上可以建立不少于四组的共线方程（甚至可以建立九组方程），从而满足外方位角元素答解的要求。

2.2 匹配同名像点

由于倾斜影像和竖直影像之间摄影角度差异较大，导致两幅影像的投影成像存在较大差别，一般的模板匹配误差较大，因此采用ASIFT算法完成匹配过程。

图3　ASIFT中的倾斜角

ASIFT算法是Jean-Michel Morel等人在SIFT算法基础上，针对两幅影像投影差别较大的问题而提出的改进算法［11］，即以影像的成像模型为基础，把待匹配的两幅影像分别看成是相机在以被摄目标为中心，摄影距离为半径的球面上成的像，这样就可以通过球面极坐标的两个角度（θ,φ）和相机自身的旋转角度ω来确定相机成像时的倾斜矩阵A，如图3所示。其中的旋转矩阵则按照下列公式进行计算：

文献［12］中即以该式为基础，把两幅图像分别按照一定的间隔对θ,φ,ω三个角度进行循环，对于每一组角度可利用成像模型得到倾斜后的图像，并对这一系列图像两两组合进行匹配，最后统计匹配成功的同名点。

根据ASIFT算法的计算流程可知，ASIFT算法的计算效率相较SIFT算法的计算效率，要低一个数量级，因此在实际应用过程中还需充分利用已知条件，减少模拟影像数量和匹配的计算量，提高匹配效率。采用ASIFT算法的匹配步骤如下：

⊙ 基于竖直影像P1，根据已知的倾斜大角度，模拟得到其倾斜影像P1'。

⊙ 以O1在模拟倾斜影像上的对应像点O1'为中心得到小区域影像P1"。

⊙ 同样根据O1'像点坐标在倾斜影像P2上得到以其为中心的小区域影像P2'。

⊙ 把P1"和P2'采用SIFT算法进行匹配，得到O1'匹配结果；如果经过匹配无法得到O1'匹配结果，则扩大P2影像上的区域范围，再进行匹配。

⊙ 重复上述步骤，直至完成整个匹配过程。

2.3 外方位元素答解

通过匹配得到控制点对应的像点坐标后，因为通过POS数据可得到精确的摄站坐标，因此可认为外方位元素中的线元素已知，则可以采用角锥体方法，通过线元素和角元素分别答解的方式，按照（3）式建立方程组，答解外方位角元素［12］［8］。

式中，（XA，YA，ZA）为模拟的控制点坐标；（xa，ya）为通过匹配得到的地面控制点对应像点坐标；Sa和SA分别为摄站点到像点和地面点的距离；a1…a3，b1…b3，c1…c3为旋转矩阵。

3 实验情况

3.1 实验区概况

实验区面积约为8平方千米，为高原平地，起伏较小，平均海拔约为1,100米。

3.2 相机参数

采用两个自制相机（一个相机竖直摄影，另一个相机倾斜摄影，倾斜角度45度），具体相机参数见表1。

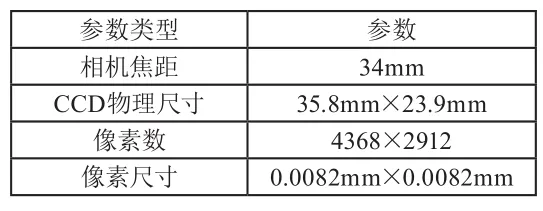
表1　相机参数

3.3 飞行参数

获取的影像分布如图4（a）所示，黑色点表示相邻竖直影像像主点所对应地面控制点在倾斜影像上（红色线框表示）的对应像点。一张倾斜像片上，根据航向多张像片和旁向多条航带像片摄站点模拟得到的控制点中选取9个作为像片控制点，并从中选择分布均匀的4个控制点作为解算控制点（如图4（b）所示），其摄站坐标和像坐标数据罗列在表3中。

表2　飞行参数

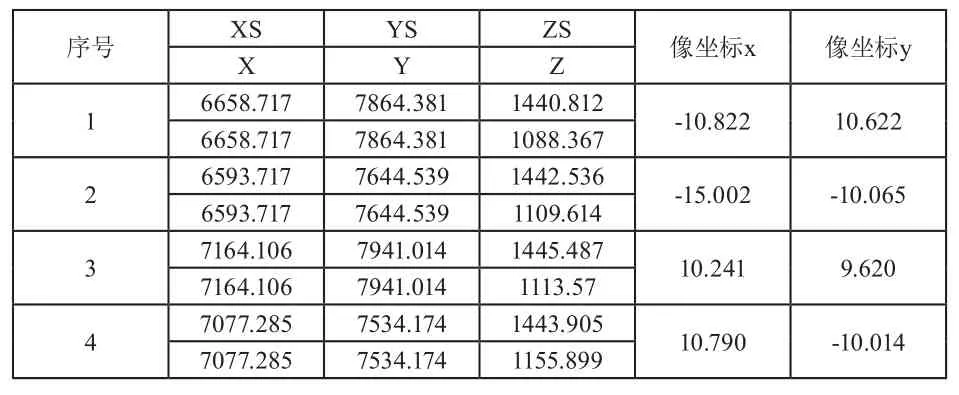
表3　四个模拟控制的坐标数据

解算得到的外方位元素如表4所列。

表4　外方位元素解算值

为了验证外方位元素的有效性，本文采用解算得到的外方位元素，对剩余的5个点分别根据像点坐标，结合5米间隔的DEM数据，解算其对应的平面坐标（X,Y），并和通过摄站坐标模拟的地面控制点坐标（X’,Y’）进行比较（高程值通过平面坐标迭代或内插得到），计算和对比情况如表5所列。

图4　航摄影像分布示意图

在表5的实验验证计算结果中，通过外方位元素反求的地面点坐标和模拟的控制点坐标之间的最大误差为-9.266米，接近1︰10万地形图的量测精度，能够满足一般情况下采用倾斜影像对地面目标进行定位的精度需求。

表5　五个验算点的计算数

4 结束语

当前国内POS数据中IMU精度不高，不能直接作为影像外方位角元素使用的现状，与在应急处置和跨境侦察等实际应用中采用大倾斜影像进行无控制定位的需求之间存在矛盾。本文针对此问题，吸收借鉴现有研究成果，对传统的单镜头倾斜摄影方式进行了改进，采用下视和倾斜两个相机组合摄影模式同时获取影像，研究了在下视影像辅助下大倾斜影像的自动化处理技术与流程，实现了无控制条件下的大倾斜影像外方位角元素解算和地面坐标量测。实验情况表明该方法计算简单，精度较好，能够满足无控制条件下倾斜影像对地观测的需求。■

参考文献

［1］ 李德仁，刘立坤，邵振峰.集成倾斜航空摄影测量和地面移动测量技术的城市环境监测［J］。武汉大学学报·信息科学版，2015,40（4）, 427-435

［2］ Ad a m R.Mosbr ucker.Applicat ion of Dig it al Oblique Photogrammetry for Monitoring Erosion and Sedimentation at Mount ST.HELNS,Washington,USA.2nd Joint Federal Interagency Conference,Las Vegas,NV. June 27-July1,2010.

［3］ G.T.Grenzdorffer,M.Guretzk,I.Friedlander. Photogrammetric Image Acquisition and Image Aralysis of Oblique Imagery -Anew Challenge for the Digital Airborne System PFIFF.

［4］ K. Jacobsen.Geomet r y of ver t ical and oblique i mage combinations［OL］,2012.03,http：//spiedigitallibrary.org/proceedings/ resource/2/psisdg/5286/1/191_1.

［5］ MassIMilianoMolinari，Stefano Medda and samir Villani. Vertical Measurements in Oblique Aerial Imagery［J］.ISPRS Int.J.Geo-Inf.2014,3：914-928.

［6］ 江刚武，姜挺，王勇等.基于单位四元素的无初值依赖空间后方交会［J］.测绘学报，2007,31（2）：169-175

［7］ 官云兰，程晓辉，周世健等.基于单位四元素的空间后方交会解算［J］.测绘学报，2008,37（1）：30-35

［8］ 张一平，龚志辉，王勃等.基于大倾角的角锥体空间后方交会研究［J］.测绘工程，2012,21（2）：17-20

［9］ 王建超，郭大海，郑雄伟等.机载POS直接地理定位的精度分析［J］.国土资源遥感，2007,（4）：33-37

［10］ 郭大海，吴立新，王建超等.机载POS系统对地定位方法初探［J］.国土资源遥，2004,（2）： 26-30

［11］ Jean-Michel More, GuoShen Yu. ASIFT： A New Framework For Fully Affne Invariant Image Comparison. SIAM J.Imaging Sciences. 2009,2（2）：438-469.

［12］ 江延川.解析摄影测量学［M］.中国人民解放军测绘学院，1991.5：37-43

Calculated Exterior Orientation Angle Elements of the Large Oblique Image with Vertical Images

Ke Ling1，2，Fan Dongjuan2，Xu Bin3
（1.Basic science department of Wuchang Shouyi University, Wuhan, 430064； 2. School of Remote Sensing and information Engineering, Wuhan University, Wuhan, 430079； 3. 73608 PLA Troop, Nanjing, 210028）

Abstract:In this paper, based on the existing research results, using vertical and oblique photography to obtain multiple images, the traditional method of photography is improved. Under the visual image assistant, the calculation of the exterior orientation angle elements of the large oblique image is realized.

Keywords:large oblique image； visual image； POS； exterior orientation elements； without control points

doi：10.3969/J.ISSN.1672-7274.2016.06.003

中图分类号：TP391

文献标识码：A 文章编码：1672-7274（2016）06-0007-04

基金项目：湖北省教育厅2015年度科研计划指导性项目（B2015200）。

作者简介：柯 玲，女，1980年生，湖北鄂州人，博士研究生，讲师，主要研究方向是数字摄影测量与遥感应用、图形图像处理、数学应用。