深部巷道围岩热-固耦合条件下的变形破坏数值分析
谭云亮,张 强
(1.山东科技大学 矿山灾害预防控制省部共建国家重点实验室培育基地,山东 青岛 266590;2.山东科技大学 矿业与安全工程学院,山东 青岛 266590)
深部巷道围岩热-固耦合条件下的变形破坏数值分析
谭云亮1,2,张强1,2
(1.山东科技大学 矿山灾害预防控制省部共建国家重点实验室培育基地,山东 青岛 266590;2.山东科技大学 矿业与安全工程学院,山东 青岛 266590)
摘要:为研究深部巷道围岩热-固耦合条件下的变形破坏特征,根据深部巷道围岩体稳态温度场模型,得出了热-固耦合条件下深部巷道围岩体应力场、位移场及塑性圈半径的解析解,总结了热应力作用下围岩变形破坏的影响因素。借助Comsol Multiphysics多物理场耦合仿真软件对深部巷道围岩进行热-固耦合数值模拟,并将岩石力学参数与温度的关系引入模拟计算,分析了热应力、支护阻力对围岩变形破坏的影响规律。仿真结果显示,围岩热应力场分布呈非线性变化,浅部应力梯度大,深部应力梯度小;当巷内温度低于原岩温度时,热应力为压应力;随原岩温度升高,径向卸压范围及切向应力集中范围扩大,围岩塑性圈宽度和径向位移值有所增大;随巷内支护阻力提高,围岩塑性圈宽度和径向位移值则有所减小。现场试验发现,巷道围岩热应力场、应力场及位移场计算结果与实测结果吻合较好。
关键词:深部巷道;温度场;应力场;热-固耦合;围岩;稳定性
深部岩体高地应力、高地温、高渗透水压力的特殊环境,构成了影响深部岩土工程稳定性的重要因素。徐燕萍等[1-2]研究了岩石在高温高压作用下的热弹塑性力学特性,推导了温度作用下的岩石热弹塑性力学特性本构方程。孟召平等[3-5]基于深部条件下不同温度和压力对砂岩力学性质的影响,建立了砂岩力学性质与温度和压力之间的相关关系,得出岩石的刚度和强度均随温度的增大而降低。左建平等[6-8]基于西原流变模型,得出热力耦合作用下西原模型的本构方程。唐世斌等[9-10]考虑岩石的非均匀性和热固耦合作用,在原有岩石破裂过程分析系统的基础上,建立了具有热固耦合作用的岩石热破裂分析模型,为从细观力学角度分析岩石的热破裂过程和机制提供了一种新的方法。张树光等[11-12]基于裂隙岩体的流-热耦合数学模型,描述了裂隙岩体渗流场分布和水流及岩体的温度场分布,并结合边界条件及计算参数对裂隙岩体的流-热耦合传热进行了数值模拟和分析,得出渗流对岩体内温度的变化规律有明显的影响。张明璐等[13]基于岩石有效应力原理修正M-C准则,以FLAC3D中的M-C模型为基础,推导修正模型H-M-C中的拉应力屈服函数,剪切、拉伸势函数,实现该模型的FLAC调用。
上述研究着重于温度影响下岩石本构模型及岩石力学性质的理论分析,缺乏从具体工程角度对其影响机理的探讨。针对深部巷道稳定性控制及支护设计,往往只关注深部高原岩应力,却忽视了深部巷道围岩的热应力场对围岩变形破坏的影响。由于巷内通风使围岩处于一个变化的温度场,即某一深度处岩层温度恒定,巷道开挖后,通风使巷道表面温度下降,与围岩发生热交换,温度变化使岩石产生热应力;另外,温度会改变岩石力学性质。因此,讨论深部巷道围岩热-固耦合条件下对围岩变形破坏的影响具有重要意义。
1热-固耦合作用下应力场分析
如图1所示,试验证明,岩石承载后变形及破坏与其所处的地温环境相关,峰值前应力-应变曲线斜率随温度增加而减小,屈服应力降低,表现为岩石强度、刚度随温度增大而减小。
岩石单轴抗压强度、弹性模量、泊松比及内聚力与温度的关系[14]为:
(1)
其中:T1为温度,℃;σ1,E1,μ1,c1分别为温度为T1时的抗压强度、弹性模量、泊松比及内聚力;σ0,E0,μ1分别为温度为0℃时的抗压强度、弹性模量及泊松比;k1,k2,k3分别为温度对抗压强度、弹性模量及泊松比的影响系数;φ为内摩擦角。
深部岩体温度较高,通过通风调节巷内温度。巷内和围岩体产生热交换,使围岩温度场分布发生改变,由此产生的热应力影响围岩体的应力分布。
对于围岩热传导问题,作如下假设[15]:
1) 围岩为均质各向同性导热体,各方向导热性能都相同;
2) 温度只沿巷道径向方向变化,走向方向上无温差;
3) 巷道为半径为a圆形水平巷道,巷道内温度呈稳态分布,恒定为Ta,受巷道内温度影响的围岩体的半径为R,此处岩体温度为原岩温度TR,处于原岩应力状态,且R≫a;
4) 巷道在开挖之前,温度为原岩温度TR,即围岩初始温度为TR。
设原岩应力为各个方向大小相等的载荷q2,圆形巷道表面设置各个方向大小相等的支护阻力q1。
因此,围岩应力场的求解就成为内半径为a,温度为Ta,外半径为R,温度为TR的厚壁圆筒形成的热应力场与原岩应力为q2,支护阻力为q1的均布载荷下固体力学应力场的叠加问题,如图2。

图1 不同温度下砂岩应力-应变曲线图

图2 深部圆形巷道围岩体热-固耦合示意图
围岩体稳定热传导方程为

(2)
边界条件为

(3)
联立式(2)、式(3)得到围岩温度场分布:
(4)
岩体变温过程中,其热应力为
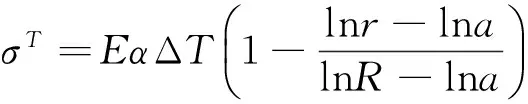
(5)
其中:α为岩石的线胀系数。
根据弹性力学中平面应变问题求解得到热-固耦合作用下应力场解析解为:
(6)
由式(6)可看出,影响深部巷道围岩应力场变化的因素包括三部分:由温度的变化ΔT所产生的热应力;支护阻力q1作用下在围岩内所产生的应力;原岩应力q2作用下在围岩中产生的应力。巷道内外存在的温差与其产生的热应力呈线性关系,即温差越大,热应力越大,反之则越小;当温差为正值即温度升高时,热应力为拉应力,反之为压应力;径向方向上支护阻力为压应力,切向方向为拉应力;径向方向和切向方向上原岩应力都为压应力。
根据侧压系数为1的受力特征,认为切向应力为最大主应力,而径向应力为最小主应力;采用莫尔-库伦准则作为进入塑性状态的条件,则起始塑性条件为
σθ=ξσr+σv。
(7)
塑性区内静力平衡方程为
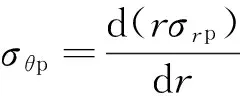
(8)
边界条件为
r=a⟹σrp=q1。
(9)
可得塑性区内应力分量为:
(10)
塑性区内的应力、应变、位移关系为:
(11)
式中:φ为塑性模数。
岩体在弹塑性交界点处满足:r=Rp;σθp=σθ;σrp=σr。可得塑性圈半径Rp及位移为:
(12)
由式(12)看出,塑性圈半径及位移不仅与岩体力学性质有关,而且受到原岩应力q2、巷道半径a、巷道内外温差ΔT及支护阻力q1的影响。
2热-固耦合条件下的巷道围岩模拟研究
借助Comsol Multiphysics多物理场耦合仿真软件进行热-固耦合分析,研究热应力、支护阻力等因素对围岩变形破坏的影响规律。模拟采用间接法,先进行固体传热分析,计算热应力场分布情况,然后将固体传热源项施加到固体力学分析计算中,并施加相应的边界条件求解。
2.1模型及模拟方案
以圆形巷道为例进行模拟计算,围岩类别参照常温状态下砂岩,特征参数见表1,并结合式(1)将砂岩力学参数与温度关系引入到模拟计算中。
由于研究区域为双轴对称平面应变问题,因此选取巷道围岩的四分之一建模,几何尺寸为15 m×15 m,巷道半径2 m。网格划分采用自由剖分三角形,计算模型共剖分为1 210个单元,总节点数为2 325。巷道附近周边网格进行加密,其他部分网格成发散状布置。

图3 网格划分及边界条件示意图
边界条件为左边界水平约束,下边界垂直约束,上边界、右边界为压力边界,大小为25 MPa。巷道内壁施加支护阻力。巷内温度恒定为20 ℃。模拟材料本构模型选用莫尔-库仑弹塑性模型。网格划分及边界条件如图3。
所采用的模拟研究方案为:
1) 保持巷内支护阻力不变(1 MPa),设定围岩初始温度分别为20,30,40,50,60 ℃。
2) 保持围岩初始温度不变,设定巷内支护阻力分别为0,1,3,5 MPa。
3) 对方案1、方案2巷道围岩的塑性圈半径及巷道表面径向位移进行监测,并与式(12)计算的理论值对比。
4) 对比分析固体力学物理场和热-固耦合物理场作用下围岩的变形破坏情况。

表1 砂岩特性参数表
2.2模拟结果
2.2.1热-固耦合作用下的应力场分布
将模拟结果与式(4)、式(5)理论解对比,实线表示模拟值,各离散点表示理论解,如图4~5所示。图4、图5分别为不同围岩初始温度下温度场和热应力场分布曲线。可以发现,巷道围岩温度场和热应力场分布呈非线性变化,且随距离和巷内温度的增大,变化梯度逐渐减小,围岩浅部变化梯度大,深部变化梯度小;围岩初始温度始终高于巷内温度,热应力在围岩内表现为压应力,其值在巷道附近最大;随围岩初始温度的升高,压应力值逐渐增大,当围岩温度为60 ℃时,压应力达到最大值10 MPa,随距巷道壁距离的增大,逐渐趋于0。无论是温度场还是热应力场,模拟值与理论值完全吻合。
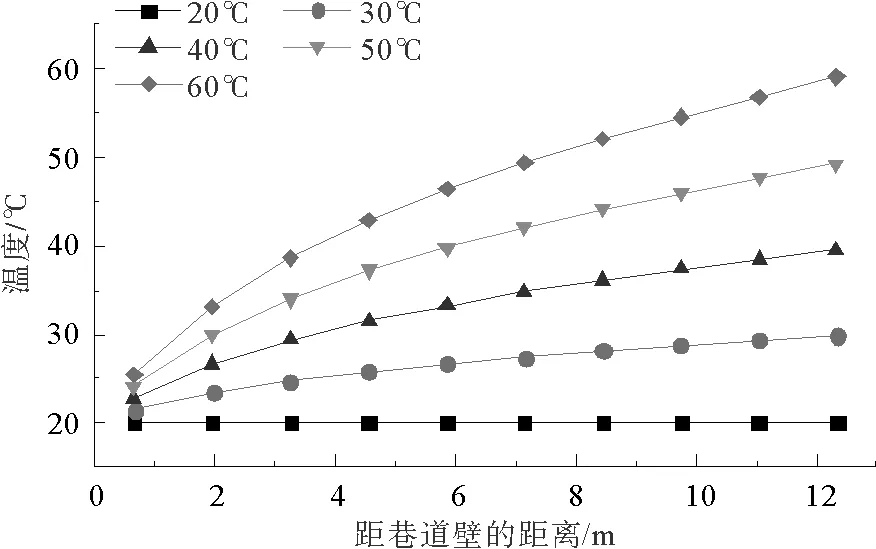
图4 围岩不同初始温度下的温度场稳态分布

图5 围岩不同初始温度下的热应力场分布
由图6和图7可以发现,巷道开挖使围岩由三向应力状态转换为二向应力状态,径向应力和切向应力在围岩内均为压应力,且巷道附近都出现一定范围的卸压区。随着围岩初始温度的升高,卸压区范围逐渐增大,对于切向应力,在巷道附近经过小范围的卸压后,出现较大面积的应力集中现象,随围岩初始温度升高,应力集中区域逐渐扩大。因为处于巷道壁附近岩体在耦合场作用下发生塑性破坏,降低了围岩承载能力,将一部分应力转移到邻近岩体,使围岩体表现为一定程度的应力集中。
耦合场作用下围岩初始温度为20 ℃时,与固体力学物理场作用下,卸压区和应力集中分布范围大体一致。因为巷内温度与围岩初始温度均为20 ℃,围岩内的温度没有发生变化,进而导致热应力值为0,对固体力学应力场没有产生影响。随着围岩初始温度的增大,卸压区和应力集中范围都有明显的增大,这是因为巷内温度低于原岩温度:一方面,由于温差引起的热应力在围岩内表现为压应力,原岩应力作用下,围岩内均表现为压应力,使得耦合场下压应力值增大;另一方面,围岩内的温度升高使得岩体的强度减小,使得围岩承载能力降低,不利于围岩体的稳定。

图6 围岩内径向应力分布

图7 围岩内切向应力分布
2.2.2热-固耦合作用下塑性圈宽度及径向位移分布
由图8和图9可以发现,巷道开挖使围岩由三向应力状态转换为二向应力状态,径向应力和切向应力在围岩内均为压应力,且巷道附近都出现一定范围的卸压区。随着围岩初始温度的升高,卸压区范围逐渐增大,对于切向应力,在巷道附近经过小范围的卸压后,出现了较大面积的应力集中现象,随围岩初始温度升高,应力集中区域逐渐扩大。因为处于巷道壁附近岩体在耦合场作用下发生塑性破坏,降低了围岩承载能力,将一部分应力转移到邻近岩体,使围岩体表现为一定程度的应力集中。
耦合场作用下围岩初始温度为20 ℃时,与固体力学物理场作用下,卸压区和应力集中分布范围大体一致,因为巷内温度与围岩初始温度相同,围岩内的温度没有发生变化,进而导致热应力值为0,对固体力学应力场没有产生影响。随着围岩初始温度的增大,卸压区和应力集中范围都明显增大,这是因为巷内温度低于原岩温度:一方面,由于温差引起的热应力在围岩内表现为压应力,原岩应力作用下,围岩内均表现为压应力,使得耦合场下压应力值增大;另一方面,围岩内的温度升高使得岩体的强度减小,围岩承载能力降低,不利于围岩体的稳定。模拟结果与理论计算结果对比发现,吻合性较好,验证了Comsol Multiphysics用于分析热-固耦合问题的适用性。
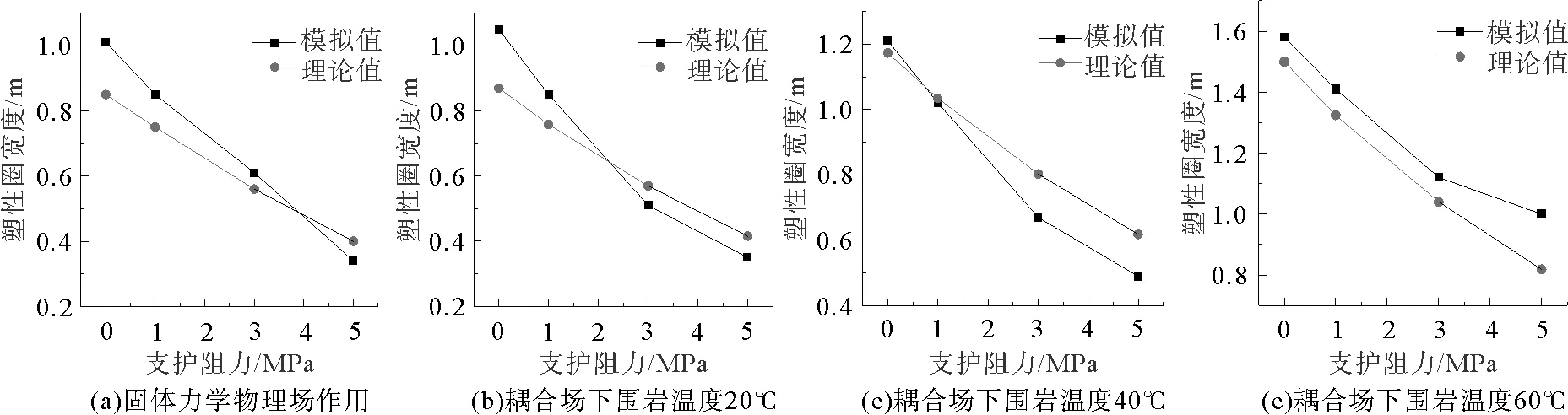
图8 围岩内塑性圈宽度分布

图9 围岩内径向位移分布
无论是固体力学物理场还是热-固耦合场作用下,随巷内支护阻力的增大,塑性圈宽度和径向位移值都有明显的减小,塑性圈宽度平均减小幅度为0.133 m/MPa,径向位移平均减小幅度为4.2 mm/MPa。耦合场作用下,随围岩初始温度的升高,塑性圈宽度和径向位移值逐渐增大,塑性圈宽度平均增大幅度为1.33 cm/℃,径向位移平均增大幅度为1.22 mm/℃,围岩初始温度为60℃时,塑性圈宽度和径向位移值达到最大,分别为1.58 m和88.3 mm。
通过数值模拟及理论分析可以发现,在巷内温度一定的条件下,随围岩初始温度的升高,径向围岩卸压圈范围增大,巷道附近岩体的应力值逐渐减小,切向应力集中范围逐渐增大,因此使得径向应力与切向应力差值随温度增大而增大。同时,岩石强度和刚度随温度增大而降低。这两个方面的作用使岩体达到屈服极限,出现塑性破坏,使得塑性圈宽度和巷道表面的位移增大。
3现场试验分析
济宁矿业集团安居煤矿东部集中轨道大巷,工作面标高为-940 m,设计断面形状为半圆拱形,巷道净宽为4.9 m,墙高为1.8 m。根据东部集中大巷地应力监测资料可知,最大水平主应力为33.19~36.69 MPa,为垂直应力的1.38~1.62倍,与巷道掘进方向夹角为4.99°~17.47°。巷道顶底板岩性均为粉砂岩、细砂岩、砂岩,岩层厚度约为50 m,围岩的力学参数及热物理学参数见表2。区内地温平均梯度值为2.26 ℃/(100 m),-940 m水平地温为35 ℃,局部地温可达40 ℃。巷道施工历时两年,在不同时期分别对巷内温度进行记录,通过数值模拟对以上条件进行热-固耦合分析,对比耦合场下不同巷内温度及不考虑热应力场作用时围岩破坏及变形情况,并对围岩的塑性区范围及位移场进行监测,以便更好地指导现场支护设计,结果如表3。

表2 围岩特性参数表
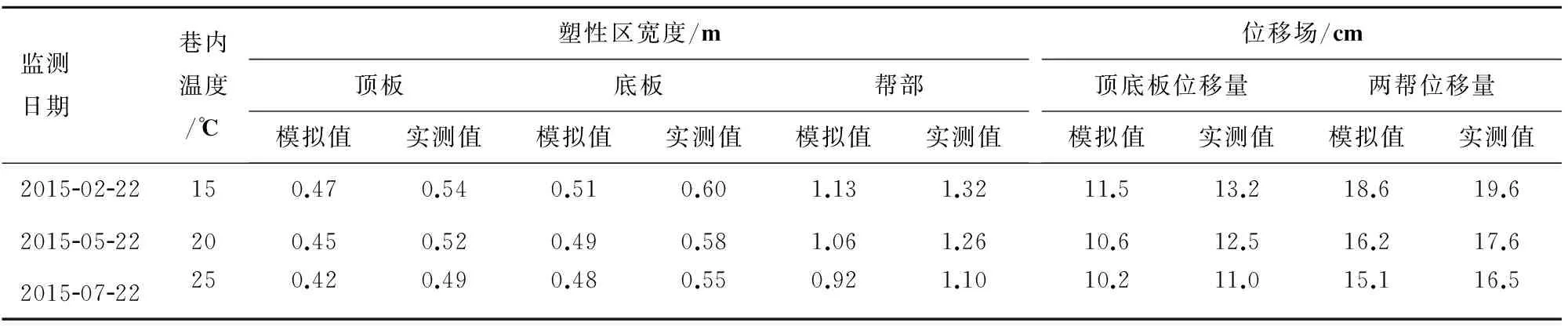
表3 围岩塑性区及位移场分布
通过对安居煤矿东部集中大巷塑性区及位移场分布数值模拟及现场实测对比分析发现,其结果基本吻合。由于在围岩初始温度保持恒定的前提下,随着巷内温度的增大,使得巷内外温差减小,由此产生的热应力也会相应减小,因此导致围岩塑性区范围及位移大小都有不同程度的减小,很好地验证了Comsol Multiphysics软件对深部高温巷道进行热-固耦合分析的正确性和适用性。
4结论
1) 热应力与围岩温度变化量成正比,塑性圈半径及位移不仅与岩体自身的力学性质有关,而且还受到原岩应力、巷道半径、巷道内外温差、支护阻力的影响。
2) 巷道围岩温度场分布呈非线性变化,在热应力作用区,随距巷道的距离的增大,温度梯度逐渐减小;热应力作为一种附加载荷叠加到原岩应力场上,改变了围岩原有的应力状态,成为影响巷道围岩稳定性的重要因素。
3) 随围岩初始温度的升高,径向卸压及切向应力集中范围扩大;同时,岩石的刚度和强度均随温度增大而降低,使岩体达到屈服极限,出现塑性破坏,使得塑性圈宽度和巷道表面的位移增大。
4) 通过数值分析和现场实测发现,巷道围岩热应力场、应力场及位移场计算结果与实测结果吻合较好。
参考文献:
[1]徐燕萍,刘泉声,徐锡昌.温度作用下的岩石热弹塑性本构方程的研究[J].辽宁工程技术大学学报(自然科学版),2001,20(4):527-529.
XU Yanping,LIU Quansheng,XU Xichang.The research on the thermo-elasto-plastic equation of the rock under the temperature effect[J].Journal of Liaoning Technical University (Natural Science),2001,20(4):527-529.
[2]王崇革,刘泉声,刘双跃,等.单轴应力下岩石的热-粘弹性模型研究[J].岩石力学与工程学报,2002,21(增1):2341-2344.
WANG Chongge,LIU Quansheng,LIU Shuangyue,et al.Study of thermo-visco-elasto-plastic rock model under the condition of uni-axial compression[J].Chinese Journal of Rock Mechanics and Engineering,2002,21(S1):2341-2344.
[3]孙天泽.高温条件下岩石力学性质的温度效应[J].地球物理学进展,1996,11(4):36-39.
SUN Tianze.Temperature effect of rock mechanics under high confining perssure[J].Progress in Geophysics,1996,11(4):36-39.
[4]夏才初,周舒威,胡永生,等.循环单轴应力和循环温度作用下玄武岩力学性质初探[J].岩土力学学报,2015,37(6):1016-1024.
XIA Caichu,ZHOU Shuwei,HU Yongsheng,et al.Preliminary study on mechanical property of basalt subjected to cyclic uniaxial stress and cyclic temperature[J].Chinese Journal of Geotechnical Engineering,2015,37(6):1016-1024.
[5]孟召平,李明生,陆鹏庆,等.深部温度、压力条件及其对砂岩力学性质的影响[J].岩石力学与工程学报,2006,25(6):1177-1181.
MENG Zhaoping,LI Mingsheng,LU Pengqing,et al.Temperature and pressure under deep conditions and their influences on mechanical properties of sandstone[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(6):1177-1181.
[6]左建平,满轲,曹浩,等.热力耦合作用下岩石流变模型的本构研究[J].岩石力学与工程学报,2008,27(增1):2610-2616.
ZUO Jianping,MAN Ke,CAO Hao,et al.Study on constitutive equation of rock rheological model with thermo-mechanical coupling effects[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(S1):2610-2616.
[7]郤保平,赵阳升,万志军,等.热力耦合作用下花岗岩流变模型的本构关系研究[J].岩石力学与工程学报,2009,28(5):957-967.
XI Baoping,ZHAO Yangsheng,WAN Zhijun,et al.Study of constitutive equation of granite rheological model with thermo-mechanical coupling effects[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(5):957-967.
[8]谭云亮,宁建国,赵同斌,等.深部巷道围岩破坏及控制[M].北京:煤炭工业出版社,2010:120-143.
[9]唐世斌,唐春安,朱万成,等.热应力作用下的岩石破裂过程分析[J].岩石力学与工程学报,2006,25(10):2071-2078.
TANG Shibin,TANG Chun’an,ZHU Wancheng,et al.Numerical investigation on rock failure process induced by thermal stress[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(10):2071-2078.
[10]李连崇,杨天鸿,唐春安,等.岩石破裂过程TMD 耦合数值模型研究[J].岩土力学,2006,27(10):1727-1732.
LI Lianchong,YANG Tianhong,TANG Chun’an,et al.Study on coupled thermal-mechanical-damage model in rock failure process[J].Rock and Soil Mechanics,2006,27(10):1727-1732.
[11]张数光,李永靖.裂隙岩体的流固耦合传热机理及其应用[M].沈阳:东北大学出版社,2014:80-105.
[12]张树光,李志建,徐义洪,等.裂隙岩体流-热耦合传热的三维数值模拟[J].岩土力学,2011,32(8):2507-2511.
ZHANG Shuguang,LI Zhijian,XU Yihong,et al.Three-dimensional numerical simulation and analysis of fluid-heat coupling heat-transfer in fractured rock mass[J].Rock and Soil Mechanics,2011,32(8):2507-2511.
[13]张明璐,赵同彬,姚旺.考虑水压影响的M-C准则修正及数值模拟[J].山东科技大学学报(自然科学版),2015,34(2):19-24.
ZHANG Minglu,ZHAO Tongbin,YAO Wang.M-C criterion modification and numerical simulation with the consideration of effects of hydraulic pressure[J].Journal of Shandong University of Science and Technology (Natural Science),2015,34(2):19-24.
[14]赵彦东,赵文奎,柯尊乾,等.温度对深井岩石力学性质的影响[J].重庆科技学院学报(自然科学版),2010,12(2):71-73.
ZHAO Yandong,ZHAO Wenkui,KE Zunqian,et al.Influence analysis of temperature on rock mechanical property in deep well[J].Journal of Chongqing University of Science and Technology (Natural Science),2010,12(2):71-73.
[15]施毅,朱珍德,李志敬.考虑温度效应时深埋硐室围岩变形特性[J].水利水电科技进展,2008,28(3):33-36.
SHI Yi,ZHU Zhende,LI Zhijing.Deformation characteristics of deep-buried caverns considering thermal effect[J].Advances in Science and Technology of Water Resources,2008,28(3):33-36.
(责任编辑:吕海亮)
Numerical Analysis of Surrounding Rock Deformation and Failure in Deep Roadway under the Condition of Thermal-solid Coupling
TAN Yunliang1,2,ZHANG Qiang1,2
(1.State Key Laboratory of Mining Disaster Prevention and Control Co-founded by Shandong Province and the Ministry of Science and Technology,Shandong University of Science and Technology,Qingdao,Shandong 266590,China;2.College of Mining and Safety Engineering,Shandong University of Science and Technology,Qingdao,Shandong 266590,China)
Abstract:To study the deformation and failure characteristics of surrounding rock in deep roadway under the condition of thermal-solid coupling,the analytical solution of stress field,displacement field and plastic circle radius in surrounding rock under the condition of thermal-solid coupling was obtained and the influencing factors of deformation and failure of surrounding rock under thermal stress was summarized based on the steady temperature field model of surrounding rock mass in deep roadway.With the multi-physical-field-coupling simulation software of Comsol Multiphysics,the thermal-solid coupling numerical simulation of surrounding rock in deep roadway was carried out and by introducing the relationship between rock mechanical parameters and temperature into the simulation calculation, the influence law of thermal stress and support resistance on deformation and failure of surrounding rock was analyzed. The results show that the thermal stress field distribution in surrounding rock is of nonlinear variation with large stress gradient in shallow surrounding rock but small stress gradient in deep surrounding rock. When the temperature in the roadway is lower than that of the original rock, the thermal stress is compressive stress and when
the temperature of the original rock increases,the pressure relief range in the radial direction and the stress concentration range in the tangential direction expand,the width of plastic circle and radial displacement of surrounding rock is increased.When the support resistance in the roadway increases,the width of plastic ring and the radial displacement of surrounding rock decrease.The field test shows that the calculated results of roadway’s thermal stress field,stress field and displacement field are in better agreement with the actual field measurements.
Key words:deep roadway;temperature field;stress field;thermal-solid coupling;surrounding rock;stability
收稿日期:2015-11-15
基金项目:国家自然科学基金项目(51274133,51474137,51474136);山东省自然科学基金重点项目(ZR2012EEZ002)
作者简介:谭云亮(1964—),男,山东临朐人,教授,博士,主要从事岩石力学科研与教学工作.E-mail:tylllp@163169.net E-mail:1039714664@qq.com
中图分类号:TD315
文献标志码:A
文章编号:1672-3767(2016)02-0029-09
张强(1991—),男,山东滨州人,硕士研究生,主要从事矿山压力与岩层控制方面的研究,本文通信作者.

