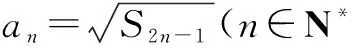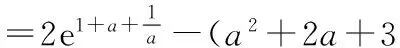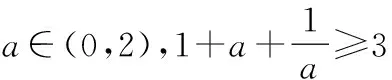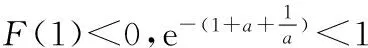高三数学综合测试
高三数学综合测试
一、填空题(本大题共14小题,每小题5分,共70分)
1.已知集合A={x|-1 2.若复数z满足iz=1+i(i为虚数单位),则z=______. 3.命题“∃x∈R,x2+x+1=0”的否定是______. 5.下面是一个算法的伪代码.如果输出的y值是20,则输入的x值是______. 6.在区间[-1,2]内随机选取一个实数,则该数为正数的概率是______. 7.在三棱锥P-ABC中,PA、PB、PC两两垂直,且PA=3,PB=2,PC=1,则三棱锥P-ABC的体积为______. 8.已知tanα=2且α为锐角,则cosα=______. 9.在平面直角坐标系xOy中,如果直线l将圆x2+y2-4x-2y=0平分,且不经过第四象限,那么l的斜率的取值范围是______. 12.设函数 若关于x的方程f2(x)-af(x)=0恰有三个不同的实数解,则实数a的取值范围是______. 二、解答题(本大题共6小题,计90分.解答应写出必要的文字说明、证明过程或演算步骤) (1)求ω的值; (2)当-1≤x≤1时,求函数f(x)的最值. 16.(本小题满分14分)在三棱锥P-SBC中,A,D分别为边SB,SC的中点,且AB=3,BC=8,CD=5.PA⊥BC. (1)求证:平面PSB⊥平面ABCD; (2)若平面PAD∩平面PBC=l,求证:l∥BC. 17.(本小题满分14分)某工厂生产某种黑色水笔,每百支水笔的成本为30元,并且每百支水笔的加工费为m元(其中m为常数,且3≤m≤6).设该工厂黑色水笔的出厂价为x元/百支(35≤x≤40),根据市场调查,日销售量与ex成反比例,当每百支水笔的出厂价为40元时,日销售量为10万支. (1)当每百支水笔的日售价为多少元时,该工厂的利润y最大,并求y的最大值; (2)已知工厂日利润达到1 000元才能保证工厂的盈利.若该工厂在出厂价规定的范围内,总能盈利,则每百支水笔的加工费m最多为多少元?(精确到0.1元) (1)求证:线段AB的长是一定值; (2)若点N是点M关于原点的对称点,一过原点O且与直线AB平行的直线与椭圆交于P、Q两点(如图),求四边形MPNQ面积的最大值,并求出此时直线MN的斜率. 19.(本小题满分16分)数列{an}是公差为d(d≠0)的等差数列,它的前n项和记为An,数列{bn}是公比为q(q≠1)的等比数列,它的前n项和记为Bn.若a1=b1≠0,且存在不小于3的正整数k,m,使ak=bm. (1)若a1=1,d=2,q=3,m=4,求Ak; (2)若a1=1,d=2,试比较A2k与B2m的大小,并说明理由; (3)若q=2,是否存在整数m,k,使Ak=86Bm,若存在,求出m,k的值;若不存在,说明理由. 20.(本小题满分16分)已知函数 (1)求函数f(x)的单调递减区间; (2)当x∈[1,2]时,f(x)的最小值是0,求实数a的值; (2)试问过点P(0,2)可作多少条直线与曲线y=f(x)相切?并说明理由. 参考答案 一、填空题 1.{0,1};2.1-i; 二、解答题 15.(1)f(x)=(a+b)·(a-b) =a2-b2 =-cos(ωx+2φ). 16.(1)∵A,D分别为边SB,SC的中点,且BC=8,∴AD∥BC,且AD=4. ∵AB=SA=3,CD=SD=5, ∴SA2+AD2=SD2, ∴∠SAD=90°,即SA⊥AD, ∴BC⊥SB. ∵PA⊥BC,PA∩SB=A,PA、SB⊂平面PSB, ∴BC⊥平面PSB. ∵BC⊂平面ABCD, ∴平面PSB⊥平面ABCD. (2)∵AD∥BC,AD⊂平面PAD,BC⊄平面PAD,∴BC∥平面PAD. ∵BC⊂平面PBC,平面PAD∩平面PBC=l, ∴l∥BC. 令y′=0,得x=31+m. ①当3≤m<4时,34≤31+m<35, ∴当35≤x≤40时,y′≤0. ∴当x=35时,y取最大值,最大值为1 000(5-m)e5. ②当4≤m≤6时,35≤31+m≤37,函数y在[35,31+m]上单调递增,在[31+m,40]上单调递减,∴当x=31+m时,y取最大值1 000e9-m. ∴当3≤m<4,x=35时,日利润最大值为1 000(5-m)e5元, 当4≤m≤6,x=31+m时,日利润最大值为1 000e9-m元. 则h(x)在[35,40]上单调增,则 ∴每百支水笔的加工费m最多约为4.9元, 答:每百支水笔的加工费m最多约为4.9元. ∴AB=3为定值. (2)设P(x1,y1),∵AB∥PQ, 点M到直线PQ:2y0x+x0y=0的距离 ∴S四边形MPNQ=2S∆MPQ 令t=3y20+1,t≥1,则 19.(1)ak=b4=33=27,即 2k-1=27,k=14,A14=196. (2)依题意,A2k=4k2,且 qm-1=2k-1,显然q>1. 所以当x>1时,f(x)>f(1)>0,即B2m-A2k>0,所以A2k (3)依题意,ak=bm=a1·2m-1. 由Ak=86Bm,得 因为29=512,故m-1≤9,且516=4×129=4×3×43,且2m-1+1为奇数, 故m-1=7,m=8且k=340. 当a≤0时,f′(x)<0在(0,+∞)上恒成立,则f(x)的单调递减区间为(0,+∞); ②a≥1,f(x)在[1,2]上单调递增,∴f(x)min=f(1)=1≠0,无解; (3)当a≤0时,有1条切线;当a>0时,有2条切线. 设切点坐标是(x0,f(x0)),依题意, 故函数F(x)在(0,+∞)上零点个数,即是曲线切线的条数. 故F(x)在(1,+e)上有且只有一个零点, 即当a<0时,F(x)在(0,+∞)上恰有一个零点. 故F(x)在(0,+∞)上至多有两个零点,且F(1)=2-2-a=-a<0. 又函数y=lnx在(1,+∞)单调递增,且值域是(0,+∞), -2-a 若a∈[2,+∞),构建函数 φ(x)在[2,+∞)为增函数, =a2+2a+3+(a2+2a+5) >a2+2a+3, ∴当a>0时,F(x)在(0,+∞)上有两个零点. 综上,a≤0时,有1条切线;a>0时,有2条切线.