双曲线中三线共点问题探究
2016-07-07 08:03:34高丰平
高中数学教与学 2016年11期
高丰平
(湖北省孝昌县第二高级中学,432900)
双曲线中三线共点问题探究
高丰平
(湖北省孝昌县第二高级中学,432900)
“三线共点”问题是双曲线中较为常见的问题.通常可以先联立两条直线方程,求出交点,再将交点坐标代入第三条直线方程中来验证.这类问题的解决往往要结合双曲线的定义、几何性质,变化较多,难度较大.下面以一道联考题引入并作一些探究.


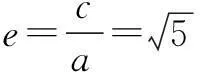

结论1自双曲线的焦点作渐近线的垂线,垂足必在相应的准线上,即过焦点所作的渐近线的垂线,渐近线及相应准线三线共点.


评注不难得到,直线DF也是圆x2+y2=a2的切线.这条性质是双曲线的一个基本性质,但有些三线共点的情况只是对一些特殊的双曲线才成立.



评注这是一类特殊的双曲线,不是所有的双曲线都有这个性质.用截距式写直线FB的方程比较方便,先求出两条直线的交点,然后由该交点也在第三条直线上来列式求解.如果把焦点换作顶点,我们又会得到一些不同的结论.

与直线l的方程bx-ay=0联立,解得
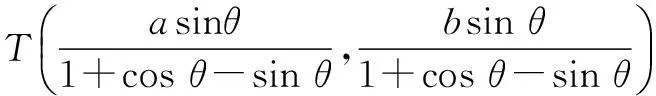



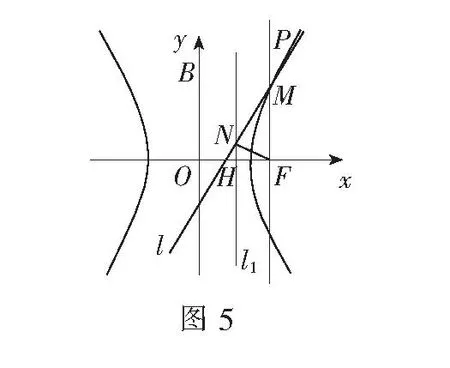

|NF|2=|HF|2+|NH|2

(*)




猜你喜欢
中学数学研究(江西)(2022年5期)2022-05-08 04:31:06
四川文理学院学报(2022年2期)2022-04-19 10:30:44
湖北农机化(2017年2期)2017-03-03 11:19:48
新高考·高二数学(2015年11期)2015-12-23 18:19:12
湖北教育·综合资讯(2015年8期)2015-11-16 19:55:46
湖北教育·综合资讯(2015年1期)2015-09-10 07:22:44
天津职业院校联合学报(2015年2期)2015-03-13 01:34:55
湖北教育·综合资讯(2014年9期)2014-10-15 20:10:52
淮北师范大学学报(自然科学版)(2014年4期)2014-07-04 06:21:46
唐山学院学报(2013年3期)2013-09-27 11:48:26

