不确定数据库频繁项集挖掘算法研究

陈凤娟（辽宁对外经贸学院基础课教研部　辽宁大连　116052）



不确定数据库频繁项集挖掘算法研究

陈凤娟
（辽宁对外经贸学院基础课教研部辽宁大连116052）

摘要：在不确定数据库中，一个项集的支持度不再是一个出现次数的累计，而是一个随机变量。因此，不像确定数据库中频繁项集有一个特定的定义，在不确定数据环境下，频繁项集有两种不同的定义。根据这两种定义，现有的频繁项集挖掘工作被分成了两类。文章主要比较这两种不同的定义以及在这些定义基础上提出的挖掘算法。

关键词：不确定数据库；期望支持度；频繁概率；频繁项集

在设计挖掘不确定数据库中的频繁项集的算法之前，如何定义频繁项集是最重要的问题。在确定数据库中，只要一个项集的支持度或频度不小于一个用户给定的最小支持度minsup，那么这个项集就是频繁的。因此，一个项集是否是频繁的是很明确的一件事。但是在不确定数据库中，情况就不同了。在不确定数据库中，一个项集是频繁的有两种不同的语义解释，一个是基于期望支持度的频繁项集，一个是概率频繁项集。这两种解释都把项集的支持度看成一个离散的随机变量，但是，二者在使用随机变量来定义频繁项集的方法是不同的。

一、不确定数据库

不确定数据库就是在数据库中包括不确定信息的数据库，根据不确定信息存在的位置不同，可以分为属性级不确定数据库和记录级不确定数据库。

在属性级不确定模型中，每一个属性值都由一些不确定的信息给出。假设一个数据库D包含n条记录，每一条记录都是由一些项组成的集合，而项的全集记为V。出现在记录tj中的V中的任意一个项v，都有一个存在概率Pr与之对应，这个概率表示的是项v属于记录tj的可能性大小，如表1所示。

表1属性级不确定数据库

记录级不确定模型中，每个记录与一个概率值相关联，即一组项的集合有一个概率。假设有数据库D，其中每个记录都是一组项的集合，并且每个记录都有一个存在概率，表示该记录在数据库D中出现的可能性大小，如表2所示。与属性级不确定数据库相比，记录级不确定数据库更简单[1]。

无论是属性级不确定数据库还是记录级不确定数据库，都可以用可能世界语义来分析。可能世界根据每个项或每个记录在数据库中出现的概率，可以计算得到其不出现的概率，用所有项或记录的出现概率和不出现的概率的乘积可以表示所有的可能性。可能世界表示了不确定事务数据库的所有可能出现的情况，属性级不确定数据库，总共有2|T|*|V|个可能世界，其中|T|是记录的总数，|V|是项的总数，而对于记录级不确定数据库，则有2|T|个可能世界，其中|T|是记录的总数。在这种假设下，不同项的出现和不出现在统计上是独立的。每个可能世界的概率可以用项集中每个单独的项的概率相乘得到，而所有可能世界的概率和为1。因此，可以把记录级不确定数据库看做属性级不确定数据库的特例。下面以属性级不确定数据库为例来分析问题。

表2记录级不确定数据库

设T是一组不同记录的集合，I是一组项的集合。一个不确定数据库D是一个从T×I到区间[0,1]的函数。不确定数据库D的一个可能世界W是T×I的一个子集。每个可能世界的概率PD(W)定义为。

设WD表示不确定数据库D的所有可能世界的集合。

一个项集X在一个可能世界W中的支持度定义为W中包含X的记录的个数，PD描述了不确定数据库的所有可能世界上的概率分布。在所有的可能世界中，我们不知道哪个可能世界是真正发生的，因此，PD表明了某个可能世界真正发生的概率。

二、期望支持度及其挖掘算法

设I={i1,i2,…,in}是一个不同项的集合，X是I的一个非空子集。用X=x1x2…xm表示项集X={x1,x2,…,xm}。如果X有m个项，则称X是一个m-项集。给定一个不确定数据库UDB，每个记录都可以表示为一个元组，其中tid是记录的标识，Y={y1(p1),y2(p2),…,ym(pm)}。Y包括m个元素，每个元素有一个项yi和一个概率pi，表示项yi在第tid个元组中出现的可能性大小。在UDB中包含项集X的记录的个数是一个随机变量，表示为sup(X)[2]。

期望支持度。给定一个包含N条记录的不确定事务数据库UDB，对于任意一个项集X，X的期望支持度是：

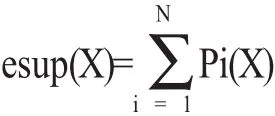
基于期望支持度的频繁项集。给定一个包含N条记录的不确定事务数据库UDB，一个最小期望支持度阈值，min_esup，一个项集X是一个基于期望概率的频繁项集当且仅当X的期望支持度大于等于N倍的最小期望支持度阈值，即esup(X)≥N×min_esup。

最具有代表性的基于期望支持度的频繁项集挖掘算法主要有三个，它们是UApriori，UFP-growth和UH-Mine。其中，UApriori算法基于生成测试框架，使用宽度优先的搜索策略。其他两个算法基于分治框架，使用深度优先的搜索策略。尽管在确定数据库中，Apriori算法比其他两个算法慢，但是它在不确定数据中的扩展算法UApriori算法在这三个算法中效率很好，并且在稠密数据库中效果最好。

UApriori算法是Chui等人在2007年提出的一个Apriori扩展算法，它把经典的Apriori算法推广到了不确定数据环境，使用生成-测试框架发现所有的基于期望支持度的频繁项集。UApriori算法首先找到所有基于期望支持度的单个频繁项，然后重复加入基于期望支持度的频繁i-项集，生成i+1项候选集，再测试i+1项候选集，得到基于期望支持度的频繁i+1项集。最后，当没有频繁项集生成时结束算法。

在不确定数据库中，向下封闭性质仍然成立。这样，当测试一个项集是否是基于期望支持度的频繁项集时，传统的Apriori剪枝策略仍然适应。也就是说，如果一个项集不是基于期望支持度的频繁项集，那么这个项集的所有超集也一定不是基于期望支持度的频繁项集。另外，还有一些对数衰减的剪枝方法来进一步提高算法的效率，这些方法主要目标是尽快找到一个项集的期望支持度的上界。一旦这个上界小于最小期望支持度阈值，那么就可以用传统的Apriori剪枝技术，删除这个项集及其所有的超集。但是，这个对数衰减剪枝方法依靠数据集的数据结构，这样，在UApriori中最重要的剪枝方法仍然是传统的Apriori剪枝[3]。

UFP-growth算法是从一个确定数据库中最有名的模式挖掘算法，FP-growth算法，扩展得到的。类似于传统的FP-growth算法，UFP-growth算法也是先建立一个索引树，称为UFP-tree，来存储不确定数据库中的所有信息。然后，基于UFP-tree结构，UFP-growth算法递归地建立条件子树，并发现基于期望支持度的频繁项集。

在建立UFP-tree的过程中，首先找出所有基于期望支持度的单个频繁项，然后依据这些单个项的期望支持度大小对它们进行排序。由这些排好序的单个项，把每个记录重新排序，然后把这些记录插入到UFP-tree中。在UFP-tree中，每个结点包括三个值。第一个值是项的标签，第二个值是这个项出现的概率，第三个值是该项从根结点到该结点共享的个数，即出现的次数。与传统的FP-tree不同，UFP-tree的压缩效果显著的降低。在UFP-tree中，必须是项的标签和其概率值都相同时，才能共享一个结点，否则，标签相同的项也必须作为两个不同的结点[4]。

UH-Mine算法也是基于分治框架的深度优先搜索算法，它是H-Mine算法在不确定数据库中的扩展，而H-Mine算法特别适合稀疏数据库。H-Mine算法首先扫描不确定数据库，找到所有基于期望支持度的单个频繁项，然后建立一个头表，用来保存所有的单个频繁项。对于其中的每个项，头表存储三个元素，项的标签，项的期望支持度和一个指针域。建立好头表后，H-Mine算法把所有的记录插入到一个新的数据结构，UH-Struct结构中。在UH-Struct结构中，每个项是仍然包括三部分，项的标签，项的期望支持度和一个指针域。算法递归的建立不同前缀的头表，生成所有的基于期望支持度的频繁项集。

三、频繁概率及其挖掘算法

对于不确定数据库，频繁概率是一个不同于期望支持度的定义。

频繁概率。给定一个包含N条记录的不确定事务数据库UDB，一个最小期望支持度阈值，min_esup，对于任意一个项集X，X的频繁概率，Pr(X)等于

概率频繁项集。给定一个包含N条记录的不确定事务数据库UDB，一个最小期望支持度阈值，min_esup，一个概率频繁阈值pft，如果一个项集X的频繁概率大于概率频繁阈值pft，则项集X是一个概率频繁项集，即

两个代表性的概率频繁项集的挖掘算法是基于动态规划的Apriori算法DP和基于分治的Apriori算法DC。精确的概率频繁项集挖掘算法首先计算或估计每个项集的频繁概率，然后仅仅返回频繁概率大于给定概率阈值的项集及其具体的频繁概率。因为频繁概率的计算比期望支持度要复杂得多，因此，对一个项集是否是概率频繁项集进行一下快速的估计能提高算法的效率。所以，一个基于概率尾不等式的剪枝策略，Chernoff边界剪枝策略，成为了提高概率频繁项集挖掘算法效率的一个重要工具[5]。

在概率频繁项集的定义下，计算项集的频繁概率是影响算法效率的关键问题。在DP算法中，采用了动态规划方法，通过把频繁概率的公式转换成，并且有P≥0，j(X)=1,0≤j≤|T|，P≥I，j(X)=0,∨i＞j，来实现动态规划。

在DC算法中，采用分治方法，把不确定数据库划分成两个子数据库，然后在两个子数据库中，算法递归地调用自己把每个子数据库再划分成两个子数据库，直到子数据库中只有一条记录为止。然后算法统计项集在这个记录中支持度的概率分布，最后，通过合并步骤，在算法结束时，获得该项集支持度的整个的概率分布。如果DC算法仅有上述的分治步骤，那么它计算频繁概率的时间复杂度同DP一样，也是O (N2)，其中，N是不确定数据库中记录的个数。但是，在合并步骤中，DC算法可以使用快速傅里叶变换方法来加速算法，最后得到的时间复杂度是O(NlogN)。在大多数情况下，DC算法要优于DP算法。

四、结语

由于现有的不确定数据库中的频繁项集挖掘有两种定义方法，因此，现存的研究也被分为了两类，基于这两种定义发展了很多挖掘方法。在今后的研究中，可以探讨这两种定义之间的联系。

参考文献：

[1]L. Wang, D.W. Cheung,R. Cheng, etc. Efficient mining of frequent itemsets on large uncertain databases [J]. IEEE Transactions on Knowledge and Data Engineering, 2011,23(3): 367～381.

[2]C. Aggarwal, P. Yu. A survey of uncertain data algorithms and applications [J]. IEEE Transactions on Knowledge and Data Engineering, 2009,21(5): 609～623.

[3]蒋涛,高云君,张彬等.不确定数据查询处理[J].电子学报,2013,41(5):966～976.

[4]李建中,于戈,周傲英.不确定性数据管理的要求与挑战[J].中国计算机学会通讯,2009,5(4):6～14.

[5]C. Chui, B. Kao, E. Hung. Mining frequent itemsets from uncertain data [C]//The Pacific-Asia Conference on Knowledge Discovery and Data Mining (PAKDD). Berlin Heidelberg: Springer-verlag,2007:47～58.

[责任编辑郑丽娟]

中图分类号：TP311

文献标识码：A

文章编号：2095- 0438（2016）05- 0149- 03

收稿日期：2016-01-10

作者简介：陈凤娟（1979－），女，辽宁本溪人，辽宁对外经贸学院基础课教研部副教授，硕士，研究方向：数据挖掘、无线传感器网络。