基于弹性波速径向变化的岩石脆裂性定量评价

唐晓明，许松，庄春喜，苏远大，陈雪莲（中国石油大学（华东）地球科学与技术学院）



基于弹性波速径向变化的岩石脆裂性定量评价

唐晓明，许松，庄春喜，苏远大，陈雪莲
（中国石油大学（华东）地球科学与技术学院）

摘要：岩石的脆性和可压裂性是非常规油气储集层体积压裂重要的岩石力学参数，为获得地层岩石的脆性和可压裂性指标，基于声波测井得到的井壁地层纵、横波速度的径向变化，求得地层的脆裂指数，指导储集层压裂改造作业。钻井过程中岩石破坏时在井壁地层中产生微裂缝，导致弹性波速度降低，波速在径向上发生由小到大的变化。采用测井纵波速度的层析成像和偶极弯曲波频散特征反演获得井壁周围地层纵、横波速度径向剖面，将两个剖面沿井径方向积分，得到纵、横波脆裂指数。脆裂指数与脆性指数、可压裂指数相关性较好，验证了用脆裂指数评估岩石脆裂性质的有效性；实际对测井数据的处理和分析亦证明了这种方法的可行性和有效性，结果对于储集层压裂优选层位和压裂改造实施有指导意义。图7表1参17

关键词：岩石脆裂性；脆裂指数；声波速度径向变化；声波测井；弹性波速

1 岩石脆裂性评价原理

非常规油气压裂开采的实践证明，地层岩石的脆性和可压裂性是影响压裂效果的关键因素。在脆性好的岩石中，当外加载荷超过岩石的破裂强度时，岩石随即起裂且裂缝的扩展不需要外加能量。反之，脆性差的岩石则会发生塑性屈服，裂缝起裂需要继续外加能量。因此，岩石的脆性是一个重要参数。但是，岩石的脆性并不等于岩石的可压裂性，如很多脆性很高的岩石，如花岗岩、白云岩等，其脆性非常高，但其强度也很高，难以压裂。因此，岩石的脆性和可压裂性共同决定要达到一定压裂效果所需的载荷大小和能量多少。这两项参数的获取亦是目前非常规油气地球物理勘探的重要内容。

目前对岩石脆性的计算一般采用矿物成分分析和弹性参数测量两种方法。在矿物成分分析法中，利用岩石中的脆性矿物，如石英、长石和方解石等所占比例得出岩石脆性指标，矿物成分数据往往通过元素俘获测井方法获得［1-3］。弹性参数测量法则通过测量地层岩石的弹性模量和泊松比定义岩石的脆性指标［4］：

岩石可压裂性的估算目前尚无成熟方法，前述分析指出该参数与岩石的强度有关，具体而言，与岩石起裂所要克服的断裂韧性有关［5］。孙建孟等人［6］提出了一种利用岩石脆性指数Br与断裂韧性KC指标估计地层岩石可压裂性的方法：

但地层岩石的断裂韧性KC值比弹性参数测量难度大，因此该方法只能作为参考。

本文提出利用钻井过程导致的井壁附近岩石波速变化来综合评估岩石脆裂性的方法。钻井的难易程度和效率与地层岩石的力学性质密切相关，岩石“可钻性”的一般定义如下：

该定义说明钻头必须要克服岩石的机械强度使其碎裂后才能在地层中钻进，因此，钻井过程本身就是对地层岩石所做的破坏性力学试验。而岩石破碎的难易程度和所需能量大小又与岩石的脆裂性质直接相关。破碎的结果是在井壁附近产生数目可观的微裂隙或裂缝。

从岩石力学角度对井壁岩石微裂隙产生的机理加以说明：钻井过程中，井内岩石碎裂后被带走，而井外岩石尚未被破坏，因此井壁岩石在钻井过程中处于破裂临界状态。对于脆性岩石而言，达此临界状态时的一个普遍岩石力学现象是岩石体积膨胀或扩容，这源于应力作用下岩石中微裂缝的产生和扩展，表现之一是岩石弹性波速（包括纵波和横波）明显降低［7］。可压裂性好的岩石容易起裂，脆性高的岩石起裂后产生的裂缝多，造成的波速降低愈明显。将此脆性岩石的扩容机理应用于扩容后的井壁岩石，不难看出岩石的脆裂性质与井壁附近波速变化的对应关系，相应地，测量这种变化及其影响范围即可评估岩石的脆裂性。钻井对井壁附近声波速度的影响已为实验室测量所验证［8］，在实际测井资料处理中也有大量实例［9］。

井壁岩石的波速降低取决于岩石中裂缝密度的大小［10-11］。但是，钻井造成的岩石变化是局部的，只发生在井筒周围，离井较远距离的原状地层却不受影响，从井壁到地层深处地层波速度呈现出由低到高的径向变化。通过求取地层波速的径向变化，可以得到井壁附近的裂隙密度及钻井影响范围，这种由钻井产生的影响大小及范围信息直接反映了钻井时岩石所体现出的脆裂性质。

2 纵、横波速度径向剖面的求取

井壁周围地层纵、横波速径向剖面的求取分别通过测井纵波速度的层析成像和偶极弯曲波频散特征的反演来获得，本文着重于方法的应用，详细原理可参见文献［9］、［12-13］。

2.1 纵波速度的层析成像

如图1所示，阵列式声波测井仪器激发的声波在波速径向增加的地层中传播，地层速度的变化使得不同接收器接收声波的径向穿透时间有所不同，这样波的走时就含有地层变化的信息，从而可以用来确定地层速度的径向变化。

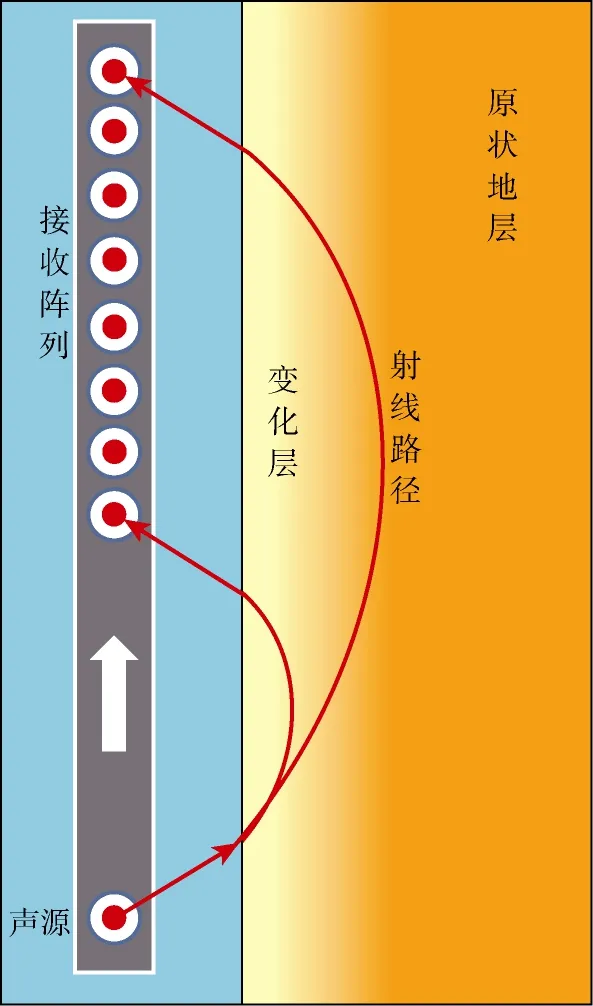
图1　速度径向变化地层中的声波射线路径示意图

Hornby［9］利用走时层析成像技术获得了井壁附近地层沿轴向和径向的二维速度剖面，即选取二维速度剖面函数v（ r， z），对其用射线追踪的方法计算得到声波走时t：

然后使计算和实测的走时之差达到最小，得到与实测数据符合最好的速度分布模型，该分布模型便描述了波速沿井轴向z和径向r的变化。

在获得地层的层析成像之前，可用一种直观有效的方法来判断目的层是否存在声波速度由低到高的径向变化。如图1所示的径向变化地层，声波射线从声源出发穿入地层后在阵列中出射，根据本多夫定理［14］，波在射线出射处沿井轴方向的视速度等于波在其最大穿透深度处的地层速度，该视速度即为波在阵列中传播的平均速度，可用阵列相关的方法［14］提取。笔者用此速度来计算声波传播到第1个接收器的走时，并将其定义为参考走时TTref，公式如下：

将公式（5）中的参考走时与实测走时比较，对于声速无径向变化的地层，参考走时与实测一致。当声速沿径向增加时，射线由浅到深进入地层后再折射回来，由于公式（5）中的v为声波所能达到的最大速度，因此由该公式计算出的参考走时比实测走时要小，实测走时滞后于参考走时。由此，通过比较实测与参考走时，即使不通过层析成像处理，也能判断地层声速是否发生了径向变化。

图2　地层声速径向变化判定图

图2为利用上述两种方法判断地层声速有无径向变化的实例，图中第2道给出了由公式（5）计算出的第1个接收器上的参考走时曲线，以及13个接收器上实测的走时曲线，对比第1个接收器上的参考走时和测量走时可以发现，后者明显滞后于前者，特别是在455～525 m、580～620 m深度段。由此可以判定这些深度段的地层发生了明显的径向速度变化。图2第3道给出了用层析成像技术反演得到的声速变化的层析成像图，ΔvP′为径向深度上纵波速度与原状地层纵波速度的相对差别的百分比：

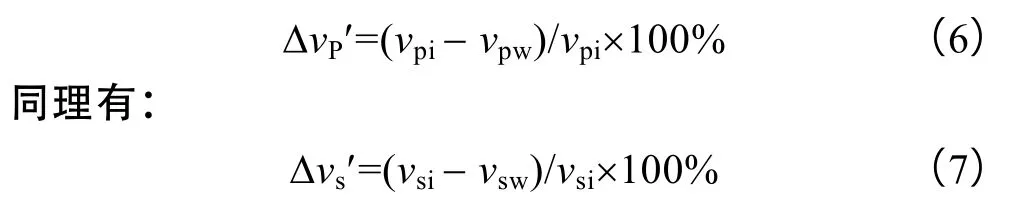
速度变化剖面的正确与否可由图2第2道曲线验证：①该速度剖面计算出的理论走时曲线（红色）是否与实测走时曲线（黑色）吻合；②实测走时相对于参考走时的滞后是否对应于速度变化剖面。图2第2道还给出了理论走时与实测走时的拟合误差曲线。当理论走时与实测走时吻合时，速度剖面的误差小，反之误差大。由图2可以看出，走时滞后明显的地带，速度剖面的变化也大，且径向影响深度明显加深。

2.2 横波速度剖面的反演

偶极横波测井通过产生沿井筒传播的弯曲波来测量地层的横波速度。研究发现，地层横波速度的径向变化会明显影响弯曲波的频散特征［15］。图3a给出了一个简单的两层径向变化模型，图3b给出了对应的弯曲波频散曲线（红线），同时还分别给出了以原状地层（蓝线）和变化层（紫线）横波速度计算出的两条均匀地层的频散曲线。对比可见，在波穿透较深的低频部分，地层的频散曲线与均匀原状地层对应的曲线一致。随着频率增加波长变短，穿透深度变浅，频散曲线又趋向于由变化层速度计算的均匀地层频散曲线。根据频散曲线的上述变化特征，得出了求取地层横波速度径向变化的约束反演方法［12-13，16］，即通过将以下目标函数极小化来实现：

上式中的反演目标函数既要求理论与实测数据在测井频段Ω中符合，又要求理论曲线vt与vh在高频区间Ω′趋于一致。后一个条件即为约束条件，通过调节权重因子λ来实现。该条件很好地消除了反演中存在的不唯一性［16］。

图4是横波波速径向反演剖面的实例，图4a为径向深度上横波速度与原状地层横波速度差别的相对百分数。为验证该速度变化剖面，对490.0 m、583.9 m深度处的频散曲线进行分析。在575.5 m处，横波速度径向剖面变化甚微，计算出的理论频散曲线与实测数据拟合很好。但在横波速度径向变化明显的490.0 m深度处，实测数据明显低于均匀地层的频散曲线（蓝线），这时须采用变化地层模型，计算出的频散曲线（红线）方能与实测数据符合，由此验证了横波速度剖面的正确性。

图3　两层地层模型及其弯曲波频散曲线

图4　横波波速径向反演剖面及频散曲线

3 纵、横波速剖面与岩石脆性指标

图2和图4中的纵、横波速度径向剖面为同一地层深度区间的结果，为了对纵、横波速度径向剖面进行定量化比较，对纵、横波速度剖面Δvp（ r）和Δvs（ r）沿井径方向积分，即：

该积分值即为岩石的脆裂指数（BFvp和BFvs，见图5），反映了纵、横波速度变化及影响区域的大小，是速度剖面变化的综合体现。图5还给出了由公式（1）和公式（2）计算的岩石脆性指数和可压裂指数曲线。对钻井时造成的岩石破裂，一般认为以剪切型破坏为主，故公式（2）中的KC取为岩石的Ⅱ型断裂韧性KⅡC（KⅡC的计算参见文献［5］）。由图5可见，纵、横波速度的径向变化剖面存在很好的一致性，两者在变化的强弱及范围上对应得很好。纵、横波脆裂指数曲线（图5第5、第6道）之间也有很好的对应性和相关性。

图5　纵、横波速度变化剖面与岩石脆裂性指数对比（GR—自然伽马；SP—自然电位；dh—井径）

纵、横波脆裂指数具相关性说明钻井过程破坏井壁岩石的同时造成了纵波和横波速度的下降。这种现象可以从孔裂隙弹性波理论［17］得到很好的解释。根据该理论，当岩石中产生了微裂隙时，岩石的体积模量和剪切模量同时改变，从而影响纵、横波的速度。因此可以认为，图中纵、横波速的径向变化是钻井过程在井壁上产生的微裂缝所致。

将纵、横波速的径向变化剖面与常规计算的脆性指数曲线（图5第7道）和可压裂指数（第8道）比较，可以看出波速径向变化的大小与脆性指数、可压裂指数的高低有很好的相关性。对于该砂、泥岩地层（见图5第2道GR、SP曲线），上部（450～525 m）的砂体较下部（580～640 m）多，故上部的脆性指数、可压裂指数总体比下部要高，对应的纵、横波速度变化也是上部比下部大；中部（525～580 m）泥岩段脆性指数、可压裂指数最小，径向剖面变化也很小。这种波速变化与脆性指数、可压裂指数相关的实质是岩石中存在裂缝。

为进一步验证上述定义的纵、横波脆裂指数的合理性和有效性，分别将纵、横波脆裂指数与岩石脆性指数、可压裂指数进行相关性分析，由图6可以看出，纵、横波脆裂指数与岩石的脆性指数、可压裂指数具有较好的相关性，平均相关系数在0.76左右；其中，横波脆裂指数与岩石脆性指数相关性最好，相关系数达0.90，表明该地层横波脆裂指数对岩石脆性最为敏感；脆裂指数与岩石可压裂指数相关性略差，相关系数约为0.60～0.70，这也说明公式（2）计算的岩石可压裂指数不够准确，仅作参考。通过对以上数据的相关性对比，说明纵、横波脆裂指数可以同时指示岩石的脆、裂性质。

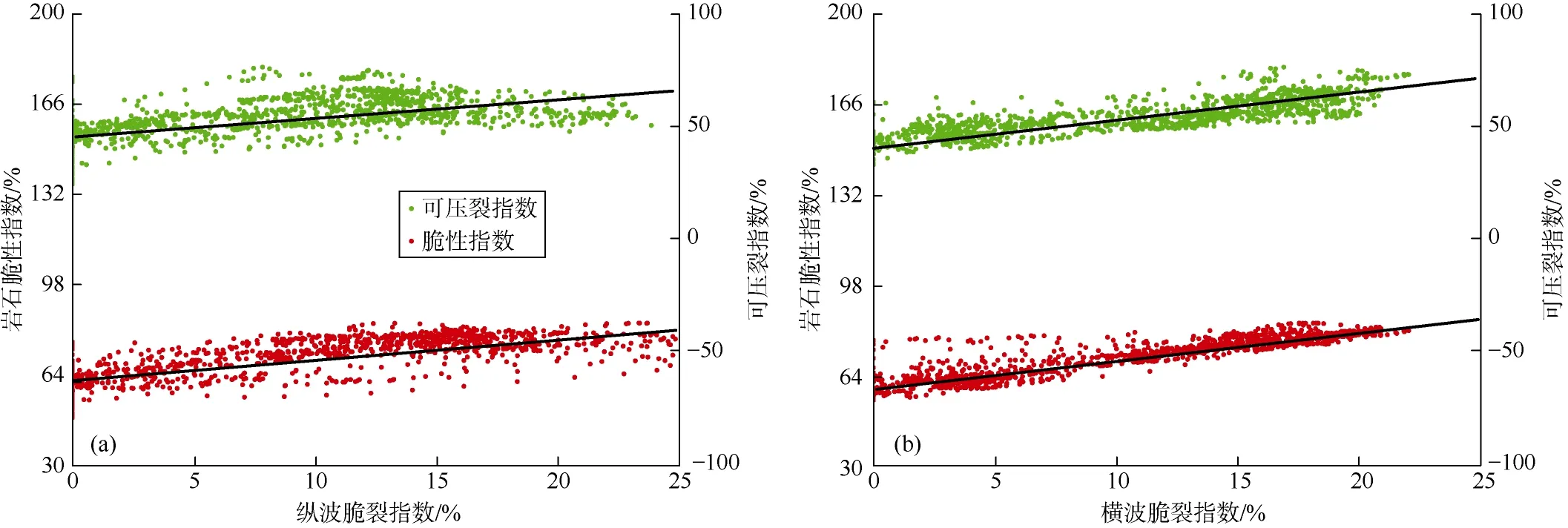
图6　纵、横波脆裂指数与岩石脆性指数及可压裂指数交会图

为进一步验证本文方法的有效性，以横波脆裂指数为例，针对同一地区10口井进行了相关性的统计（见表1），结果表明该地区横波速度的径向变化与岩石的脆裂性质有较好的相关性，从统计意义上进一步验证了用波速径向变化剖面评估岩石脆裂性质的有效性。

表1　某一地区岩石横波脆裂指数与岩石脆性指数、可压裂指数的相关性统计

需要指出的是，本文定义的脆裂指数并不等同于常规方法得到的脆性与可压裂性。如公式（1）的脆性指数，根据声波测井原理，弹性参数法中计算弹性模量和泊松比时所用弹性波速是穿过径向变化区域以外的原状地层速度，与速度变化区无关。公式（1）的脆性指数与岩石基质有关，而公式（9）考虑速度变化计算的脆裂指数与基质破坏产生的裂缝有关，两者并不等同，它们之间的相关性是由于外力作用后基质中产生裂缝引起的。

4 脆裂指数在指导压裂改造中的应用

图7为利用脆裂指数指导致密储集层压裂改造的综合应用实例，由图中自然伽马曲线可知该井947～977 m段为（致密）砂岩；图中第3道为偶极波形变密度图，可以看出声波波形在储集层段的波形质量较好；第4道为利用偶极横波反演的径向距离1 m范围内的横波速度变化剖面，可以看出，在947～977 m井段附近，地层横波速度径向变化特征较明显，变化带横波速度明显小于原状地层横波速度。图7中第5道是由该剖面积分计算出的横波脆裂指数曲线，该指数可以用来综合评估岩石脆性和可压裂性。

综上所述，947～977 m储集层段径向横波速度变化较大，岩石更易破碎，同时储集层顶部脆裂指数变化相对底部要小，说明顶部岩石相对底部可压裂性较差且破裂压力偏大。因此，为了将整个储集层压开，应选择在顶部进行压裂施工，这样在压裂顶部的同时也会把脆裂性较好的底部井段压开。第6道是压裂后测得的正交偶极快、慢横波波形，两波之间的明显分异说明该井段存在较大的各向异性［15］。第7道为压裂前、压裂后横波各向异性。该储集层上方地层各向异性在压裂前、后无大的变化，但储集层部位压后各向异性较压前明显增大，说明储集层被压开，并且开始产气，压裂效果理想。这一实例说明了本文方法得到的脆裂指数在指导地层压裂改造应用中的有效性。

图7　致密储集层横波速度剖面与多种测井结果对比图

5 结语

钻井过程会导致井壁岩石扩容，在岩石中产生微裂缝。裂缝数目的多少、影响区域的大小与岩石的脆裂性——脆性和可压裂性密切相关，而裂缝的存在会同时造成纵、横波速的径向变化。通过求取井壁岩石波速的径向变化，可以有效评估地层岩石的脆裂性。这种有效性已为大量数据所证实。本文方法可指导非常规油气储集层压裂改造作业。

符号注释：

BFvp——纵波脆裂指数，无因次；BFvs——横波脆裂指数，无因次；Br——岩石的脆性指数，无因次；DB——岩石可钻性，无因次；E——地层弹性模量，GPa；EOBJ——约束反演方法目标函数，m2/s2；Fr——地层可压裂指数，无因次；KC——岩石断裂韧性，MPa·m1/2；r——径向位置，m；Δr——波速变化区域大小，m；R——井眼半径大小，m；s——声波传播的最短路径，m；t——声波走时，s；TTf——声波在井筒流体中的传播时间，s；TTref——参考走时，s；v——地层速度，m/s；Δv——波速变化大小，m/s；v（z）——阵列处理提取的地层声速函数，m/s；vd——阵列弯曲波提取的频散曲线函数，m/s；vh——井壁地层横波速度计算的均匀地层频散曲线函数，m/s；vpi——原状地层纵波波速，m/s；vpw——钻后实际地层纵波波速，m/s；vsi——原状地层横波波速，m/s；vsw——钻后实际地层横波波速，m/s；vt——径向变化模型理论频散曲线函数，m/s；ΔvP——纵波波速变化，m/s；ΔvP′——纵波波速变化率，%；Δvs′——横波波速变化率，%；Δvs——横波波速变化，m/s；z——声波波形数据采集的深度，m；zr1——第1个接收器深度，m；zs——声源深度，m；λ——权重因子，无因次；ω——角频率，Hz；ν——地层泊松比，无因次；Ω——测井频段，Hz；Ω′——高频处理频段，Hz；σc——岩石单轴抗压强度，MPa；σt——岩石单轴抗拉强度，M P a。下标：m a x——最大值；m i n——最小值；N——归一化值。

参考文献：

［1］PEREZ A R， MARFURT K.Mineralogy-based brittleness prediction from surface seismic data： Application to the Barnett Shale［J］.Interpretation， 2014， 2（4）： T255-T271.

［2］刘绪纲， 孙建孟， 郭云峰.元素俘获谱测井在储层综合评价中的应用［J］.测井技术， 2005， 29（3）： 236-239.LIU Xugang， SUN Jianmeng， GUO Yunfeng.Application of elemental capture spectroscopy to reservoir evaluation［J］.Well Logging Technology， 2005， 29（3）： 236-239.

［3］WU H L， LI N， LAN C L， et al.Standard spectrum measurement and simulation of elemental capture spectroscopy log［J］.Applied Geophysics， 2013， 10（1）： 109-116.

［4］RICKMAN R， MULLEN M， PETER E， et al.A practical use of shale petrophysics for stimulation design optimization： All shale plays are not clones of the Barnett Shale［R］.SPE 115258-MS， 2008.

［5］袁俊亮， 邓金根， 张定宇， 等.页岩气储层可裂性评价技术［J］.石油学报， 2013， 34（3）： 523-527.YUAN Junliang， DENG Jin'gen， ZHANG Dingyu， et al.Fracability evaluation of shale-gas reservoirs［J］.Acta Petrolei Sinica， 2013，34（3）： 523-527.

［6］孙建孟， 韩志磊， 秦瑞宝， 等.致密气储集层可压裂性测井评价方法［J］.石油学报， 2015， 36（1）： 74-80.SUN Jianmeng， HAN Zhilei， QIN Ruibao， et al.Log evaluation method of fracturing performance in tight gas reservoir［J］.Acta Petrolei Sinica， 2015， 36（1）： 74-80.

［7］陈颙， 黄庭芳， 刘恩儒.岩石物理学［M］.合肥： 中国科技大学出版社， 2004.CHEN Yong， HUANG Tingfang， LIU Enru.Rock physics［M］.Hefei：China University of Science and Technology Press， 2004.

［8］WINKLER K W.Borehole damage indicator from stress-induced velocity variations［J］.Geophysics， 2005， 70（10）： F11-F16.

［9］HORNBY B E.Tomographic reconstruction of near-borehole slowness using refracted borehole sonic arrivals［J］.Geophysics，1993， 58（12）： 1726-1738.

［10］THOMSEN L.Biot-consistent elastic moduli of porous rocks：Low-frequency limit［J］.Geophysics， 1985， 50（12）： 2797-2807.

［11］TANG Xiaoming， CHEN Xuelian， XU Xiaokai.A cracked porous medium elastic wave theory and its application to interpreting acoustic data from tight formations［J］.Geophysics， 2012， 77（6）：D245-D252.

［12］TANG X M， PATTERSON D J.Mapping formation radial shear-wave velocity variation by a constrained inversion of borehole flexural-wave dispersion data［J］.Geophysics， 2010， 75（6）：E183-E190.

［13］SU Y D， TANG X M， ZHUANG C X， et al.Mapping formation shear-velocity variation by inverting logging-while-drilling quadrupole-wave dispersion data［J］.Geophysics， 2013， 78（6）：D491-D498.

［14］徐果明， 周蕙兰.地震学原理［M］.北京： 科学出版社， 1982.XU Guoming， ZHOU Huilan.Principle of seismology［M］.Beijing：Science Press， 1982.

［15］唐晓明， 郑传汉.定量测井声学［M］.北京： 石油工业出版社， 2004.TANG Xiaoming， ZHENG Chuanhan.Quantitative acoustic well logging［M］.Beijing： Petroleum Industry Press， 2004.

［16］赵龙， 唐晓明， 苏远大， 等.横波速度径向层析成像方法及应用研究［J］.应用声学， 2014， 33（1）： 9-15.ZHAO Long， TANG Xiaoming， SU Yuanda， et al.Research on radial shear-wave velocity tomography［J］.Journal of Applied Acoustics，2014， 33（1）： 9-15.

［17］唐晓明.含孔隙、裂隙介质弹性波动的统一理论-Biot理论的推广［J］.中国科学： 地球科学， 2011， 41（6）： 784-795.TANG Xiaoming.A unified theory for elastic wave propagation through porous media containing cracks： An extension of Biot's poroelastic wave theory［J］.SCIENCE CHINA Earth Sciences， 2011，54（9）： 1441-1452.

联系作者：陈雪莲（1976-），女，河北衡水人，博士，中国石油大学（华东）副教授，主要从事声波测井方法及岩石物理学方面的教学和科研工作。地址：山东省青岛市黄岛区长江西路66号，中国石油大学地球科学与技术学院，邮政编码：266580。E-mail：chenxl@upc.edu.cn

（编辑 黄昌武）

Quantitative evaluation of rock brittleness and fracability based on elastic-wave velocity variation around borehole

TANG Xiaoming， XU Song， ZHUANG Chunxi， SU Yuanda， CHEN Xuelian
（School of Geosciences & Technology， China University of Petroleum， Qingdao 266555， China）

Abstract：Brittleness and fracability are two important rock properties in hydraulic fracturing of unconventional reservoirs.Based on the variation of compressional and shear velocity around borehole using acoustic measurement， an effective technique is developed to estimate these parameters to guide reservoir-fracturing.During drilling， when the rock is broken， a significant amount of drilling induced cracks will occur in the formation around the borehole， resulting in the drop of radial elastic wave velocity and the wave velocity variation from low to high in radial direction.The radial variation of compressional and shear velocities of formation rocks surrounding a borehole were respectively obtained from P-wave travel time tomography and dipole shear-wave dispersion inversion.By integrating the two variation profiles along the radial direction， the brittleness-fracability index is obtained to estimate the brittleness and fracability of formation rocks.The index shows fairly good consistency and correlation with rock brittleness and fracability， which demonstrates the practicability and effectiveness of the proposed approach.Well log data analysis examples are presented to demonstrate the effectiveness of our technique.

Key w ords：rock brittleness-fracability； brittleness-fracability index； radial acoustic velocity variation； acoustic well logging；elastic-wave velocity

中图分类号：P618

文献标识码：A

文章编号：1000-0747（2016）03-0417-08

DOI：10.11698/PED.2016.03.12

基金项目：国家重点基础研究发展计划（973）项目（2014CB239006）；国家自然科学基金（41474101，41474092）；中央高校基本科研业务费专项资金（14CX05010A，16CX06040A）；山东省自然科学基金（ZR2014DL009）

第一作者简介：唐晓明（1955-），男，四川雅安人，博士，中国石油大学（华东）教授，主要从事地球物理（声波）测井、岩石物理学、地震波传播及测量等方面的研究和技术开发工作。地址：山东省青岛市黄岛区长江西路66号，中国石油大学地球科学与技术学院，邮政编码：266580。E-mail：tangxiam@aliyun.com

收稿日期：2015-03-05 修回日期：2016-03-29