脱湿状态下南京下蜀土的土水-力学特性*

韩爱民　李　彤　徐洪钟

( 南京工业大学，岩土工程研究所南京210009)

脱湿状态下南京下蜀土的土水-力学特性*

韩爱民李彤徐洪钟

( 南京工业大学，岩土工程研究所南京210009)

摘要用经改造的GDS非饱和土三轴仪测得下蜀土在不同净围压下的变形特性和持水特性，并以van Genuchten模型对试验数据的拟合结果为基础，分析了净围压对下蜀土吸力应力特征曲线的影响，全面系统地研究了脱湿状态下南京下蜀土的土水-力学特性。研究表明，下蜀土的变形特性受净围压与基质吸力影响，基质吸力越高，下蜀土的压缩性越低，可以用二元指数函数本构模型分析孔隙比与应力状态变量间的关系。净围压使下蜀土持水能力增强，净围压与进气值呈幂函数关系。土的压缩性越高，净围压对其持水特性的影响越显著； 随着净围压的增大，下蜀土孔隙比趋同，净围压对持水特性的影响逐渐减弱。外部荷载对下蜀土吸力应力特征曲线的影响是分段的，在边界效应区范围内，净围压增大时，吸力应力特征曲线间的差异逐渐减小； 在过渡区范围内，吸力应力随状态变量变化的快慢程度不受外部荷载影响。根据双电层理论分析了高吸力时吸力应力的物理意义与计算方法，提出以界限有效饱和度作为吸力应力函数的分界点。

关键词下蜀土净围压压缩性土水特征曲线吸力应力

李彤(1990-)，男，硕士生，主要从事非饱和土方面的研究工作.Email:gnotil80@163.com

Xiashuloess,Netconfiningpressure,Compressibility,Soil-waterretentioncurve,Suctionstress

0引言

下蜀土广泛分布于长江中下游的不同高度和不同地貌单元(郑乐平等， 2002)，分布区域经济相对发达、人口比较密集，承受了强度和频度都比较高的开发利用。自然状态下，位于阶地的下蜀土有着良好的工程力学性质(韩爱民等， 2013)，因此，常被作为建筑物、道路的地基加以利用，改良后的下蜀土甚至用作高铁轨道的路基(孙宏林等， 2004)。由于下蜀土的低压缩性和低渗透性，亦用作填料或防渗材料(顾凯等， 2011)。在下蜀土边坡稳定性评价与加固设计方面，也积累了相当多的地区经验。

然而，下蜀土是一种具有双重工程特性的区域性土(高国瑞等， 2005)，我们把自武汉、黄石、九江、安庆、芜湖至南京、镇江沿长江两岸分布的下蜀土联系起来，发现这些被山脉和丘陵分割的黏性土有着一些共同特点，即具有基本相同的主要黏土矿物成分(伊利石)和不同程度的胀缩性(Gao， 1998)。正因为如此，在干湿两种不同状态下，下蜀土的工程性质表现出极大的差异性(夏佳等， 2001)，其工程地质性质受水的影响尤其明显，其分布地区滑坡地质灾害形势非常严峻。据统计，南京市共有下蜀土滑坡地质灾害隐患点263处，总面积1281.9km2，其中高易发区面积111.5km2。目前，对土水特征曲线及其相关性研究多集中于黄土、膨胀土及红土，对于原状下蜀土的土水-力学特性作用规律的相关研究甚少。因此，以南京下蜀土的土水特征曲线量测为基础，分析南京下蜀土的土水-力学特性，对下蜀土分布地区的滑坡地质灾害防治具有重要意义。

土水特征曲线(soil-waterretentioncurve，SWRC)是土中吸力与饱和度或体积含水率之间的非线性关系曲线，是用于解释非饱和土水理-力学性质的基本本构关系，被广泛应用于分析与推测非饱和土的渗透性、体变、强度、吸力应力等众多性质。目前常用的土水特征曲线量测方法，如压力板仪法、热敏传感器法、蒸汽平衡法、渗析法及滤纸法的原理是量测极限应力状态下试样的土水特征曲线，未考虑土体变形、应力状态对土水特征曲线的影响； 而天然状态下的非饱和下蜀土通常处于非极限应力状态，且非饱和土的体积变化与持水特性存在力-水耦合效应，其力学与水力学行为同时发生且相互影响(周葆春等， 2015)，导致上述量测方法在研究原状下蜀土的土水特征曲线时存在局限。非饱和土固结仪可以控制试样中的竖向应力，但无法测得试样中的径向应力； 应力式体积压力板仪(龚壁卫等， 2004)与非饱和土三轴仪虽然可以精确控制试样的应力状态并量测试样体变，但完整试样体积较大，试验用时较长。所以，通过降低三轴试样的高度，可以在精确量测试样的应力状态及体变的同时，有效缩短试验时间。

所以，作者以原状下蜀土为研究对象，开展脱湿状态下南京下蜀土的土水-力学特性试验研究。利用GDS非饱和土应力路径三轴仪量测小体积试样在不同应力状态下的基质吸力、体积与含水率变化，得到以孔隙比-基质吸力-净围压间数学关系表达的土结构本构面与等吸力压缩曲线，分析非饱和下蜀土的非线性力-水耦合效应； 同时，从非饱和土力学的角度，揭示下蜀土压缩性存在层间差异这一地质现象的力学本质。运用vanGenuchten模型对不同净围压下南京下蜀土的土水特征曲线进行拟合，分析进气值随应力状态变化的内在机理与两者间的经验关系； 通过分析不同净围压下土水特征曲线的客观差异，解释随着净围压的增大，下蜀土持水特性的增强趋势渐缓的现象，并进一步探讨土的压缩性-净围压-持水特性之间的关系。以土水特征曲线拟合结果为基础，推算不同净围压下的吸力应力特征曲线(suction-stresscharacteristiccurve，SSCC)，分析外部荷载对下蜀土吸力应力特征曲线影响的分段性特征； 根据双电层理论分析黏粒间电-化学力与结合水状态的关系，探讨高吸力时吸力应力的物理意义，以及分段型吸力应力函数的计算方法。通过一系列试验研究分析，对下蜀土的土水-力学特性有了全面系统的新认识，丰富了非饱和土力-水耦合研究成果。

1研究方法及试验方案

1.1试验用土基本参数

本试验以原状下蜀土为研究对象。原状土样取自南京地铁三号线五塘村站北侧幕府山南麓。土样参数(表1)。

表1　试验用下蜀土基本参数

1.2试验原理及设备

GDS非饱和土应力路径三轴试验系统主要包括GDSLAB软件，Bishop&Wesley型三轴压力室和压力控制器，压力控制器测量水/空气体积精度为1mm3。通过对试样施加围压(σ)、反压(uw)及气压(ua)，测得下蜀土在不同净围压(σnet=σ-ua)与基质吸力(s=ua-uw)下达到平衡状态时的体积与排水量。由于GDSLAB软件未配备针对土水特征曲线量测的模块，试验中的各项体积、压力值需人工记录。

本试验采用扁平小试样进行试验，方便确定平衡状态。试样直径38.0mm(500kPa进气值陶土板底座直径38.00mm)，厚4.5mm。

通过试样体积测量装置间接量测试样体积，(图1)。通过记录试样左右两侧钢针在透明刻度尺上正投影处的示数Lli和Lri，以及试样高度H(由竖向透明尺读出)，根据式(1)-(2)计算不同时刻试样体积V。其中，D为试样直径，d为同向水平钢针间橡胶膜厚度。

(1)

(2)

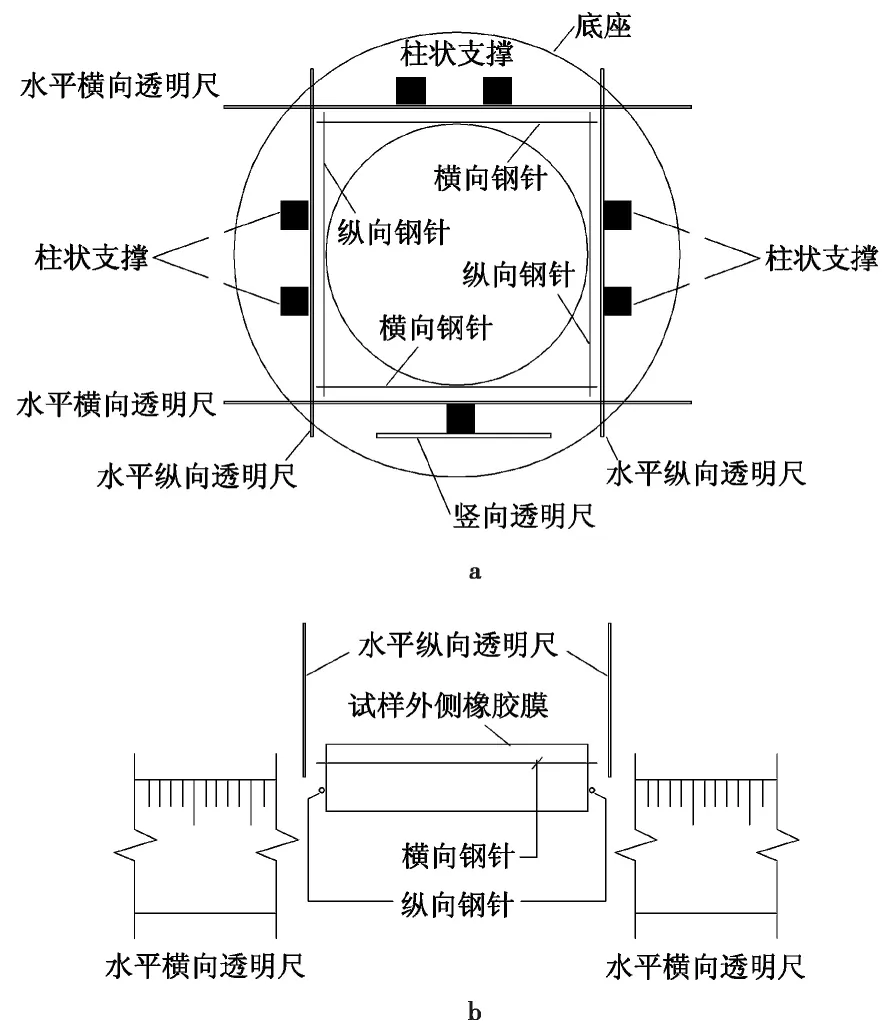
图1　试样体积测量装置示意图Fig. 1　Specimen volume measurement devicea.俯视图； b.部分侧视图

1.3试验步骤

第1步：饱和试样、陶土板及透水石。

第2步：在底座上安装试样及试样体积测量装置。

第3步：安装压力室，在压力室内充满无气水。

第4步：以饱和试样固结完成作为试验起算点，按表2安排试验。试验室气温控制在25～27℃(蔡国庆等， 2010； 王媛等， 2010)。试验中达到每一级平衡状态需1～4d。

图2为试验完成后的试样，侧面变形均匀。如表3所示，对比利用试样体积量测装置与游标卡尺对脱湿完成试样的量测结果，表明试样体积的量测计算满足试验要求。

表2　试验方案

由于气体扩散与透水石中水的影响，需要对反压体积变化量进行修正。从反压体积变化量中分别减去通过扩散试验得到的气体扩散体积以及透水石排水体积(梅岭等， 2013)，修正试样达到不同平衡状态时的排水量。

图2　脱湿完成后试样外观Fig. 2　Specimen after moisture desorption

表3　试样体积量测计算的校验

2试验结果分析

2.1变形特性

非饱和下蜀土是气-水-土三相混合体，在气压与围压共同作用下产生连续变形。净围压作用使得土结构中的粒状及絮状胶结结构产生压缩变形，孔隙中气压的存在使得自由水减少。同时，毛细水的非连续分布随着气压的增加而愈加显著，导致构成粒状、絮状胶结物质的黏土矿物叠聚体产生干缩变形。可以通过建立描述孔隙比(e)与应力状态变量基质吸力、净围压之间关系的本构面，分析控制土骨架变形的非线性力-水耦合效应。

式(3)是图3中曲面的三维几何方程，即利用数学方法建立的孔隙比与净围压、基质吸力间的本构关系

(3)

式中，er为在不同净围压与基质吸力共同作用下，下蜀土可能达到的最小孔隙比； edv为原状下蜀土孔隙比与er的差值； b、c为拟合参数，单位为kPa。此例中er、edv、b、c的数值分别为0.5644、0.1174、171.2271、167.3129，拟合相关系数R2为0.9684。

在孔隙比单调减少的路径下，即净围压与基质吸力单调增大时，该本构面是唯一的(Matyasetal.，1968)； 所以，本构面在(σnet-e)平面上的投影，即为不同基质吸力下的等吸力压缩曲线(图4)。随着基质吸力的增大，压缩模量逐渐增大，下蜀土的压缩性降低。下蜀土由西北黄土状土经风力、水力搬运堆积至长江流域，在饱水状态下沉积而成(Zhangetal.，2007)。不同基质吸力下的压缩曲线，解释了下蜀土经地质作用抬升后饱和度降低(韩爱民等， 2009)，压缩模量随埋藏深度减少而升高(Xiaetal.，2009)的现象。

图3　土结构的本构面Fig. 3　Constitutive surface of soil structure

图4　等吸力压缩曲线Fig. 4　Compression curves with different matric suction

2.2土水特征曲线

如图5，下蜀土在不同净围压下具有不同的持水特性，可采用vanGenuchten模型(VanGenuchten， 1980)分析体积含水率(θ)与基质吸力(s)间的关系

(4)

式中，θr和θs分别为残余体积含水率和饱和体积含水率； α、n为拟合参数。设定θr=0(Phoonetal.， 2010)，消除基质吸力实测值范围偏小时该模型拟合参数的多解性(谭晓慧等， 2013)，计算结果(表4)。

表4　土水特征曲线拟合参数

图5　以s-θ关系表述的的土水特征曲线Fig. 5　SWRCs in s-θ form

可以看出，净围压的增大使得下蜀土结构受到压缩，可压缩孔隙(Phametal.，2011)变小，进气值升高； 净围压越大，达到相同基质吸力时，可压缩孔隙中的毛细水液面弯曲程度越低，相同基质吸力变化量对应的体积含水率变化量越低，这一点与重塑下蜀土(梅岭等， 2013)性质相同。由于以饱和试样固结完成作为脱湿试验起算点，且当气压大于进气值后下蜀土的压缩性显著降低，经历较长时间的收缩后，试样的孔隙比逐渐接近er，相同基质吸力变化量对应的体积含水率变化量趋于一致，下蜀土在不同净围压下的持水特性趋于一致。

图6给出了下蜀土及其他两种粉质黏土的进气值(air-entryvalue，AEV)与净围压的关系，鄂西北膨胀土(龚壁卫等， 2004)与粗高岭土(Thuetal.，2007)的土水特征曲线分别采用应力式体积压力板仪与非饱和土三轴仪测得。相同净围压变化量对应的进气值增量逐渐降低，可以用幂函数表达进气值与净围压的关系。

(5)

式中，AEV0为净围压为0时土的进气值，拟合参数λ与土的压缩性相关。土的压缩性越高，孔隙体积(Vv)的相对变化量(ΔVv/Vv)在净围压作用下变化越大，相同净围压增量对应的进气值增量越大，与λ正相关的σnet-AEV关系曲线倾斜程度越大。其中，原状下蜀土压缩系数a1-2为0.20MPa-1，λ约为a1-2的3.79倍。该函数可以较好地描述不同净围压下3种粉质黏土进气值的增大趋势。

图6　不同净围压下土的进气值Fig. 6　AEVS under different net confining pressure

由于θr=0，式(4)可以写成

(6)

式中，Se为有效饱和度。图7 中的计算拟合值所用的参数α与n与图5 中的一致。净围压为50kPa与100kPa时，相同基质吸力对应的有效饱和度的差值先逐渐增大，当基质吸力超过进气值后，差值逐渐稳定，即s-Se曲线的后半段近似平行。而净围压为100kPa与150kPa时的s-Se曲线基本重合，说明随着净围压的增大，相同基质吸力对应的有效饱和度逐渐接近。

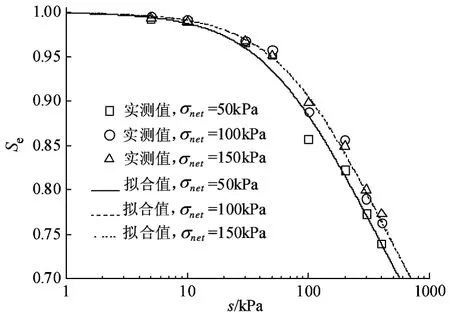
图7　以s-Se关系表述的的土水特征曲线Fig. 7　SWRCs in s-Se form

图8　Al-Qatif膨胀土的土水特征曲线Fig. 8　SWRCs of Al-Qatif expansive clay

根据图7 及图8，下蜀土在基质吸力为5～400kPa范围内， 3组试样间有效饱和度差值在0.5%以内，应力状态对脱湿状态下下蜀土饱和度变化的影响并不显著。然而，初始孔隙比与压缩性均高于下蜀土的Al-Qatif膨胀土(Elkadyetal.，2015)，在7kPa、100kPa及600kPa的净竖向压力(σv-net=σv-ua)作用下，脱湿至基质吸力为400kPa时饱和度分别降低约18%、3%及1%，它们之间的差值远大于下蜀土的0.5%。可见土的压缩性越高，净围压对持水特性的影响越显著。

2.3吸力应力特征曲线

吸力应力是受颗粒间的胶结物质及孔隙水性状控制的颗粒间相互作用力，由物理-化学力、黏结力、黏粒表面作用力、毛细水表面张力构成(Luetal.，2006)，前3种力主要由黏粒表面电-化学作用产生。Lu(2008)认为基质吸力作为应力状态变量，需要转化为吸力应力这一应力变量，才能直接用于建立体现基质吸力对土强度及变形特性影响的气-水-土单元体平衡方程，并提出利用土水特征曲线试验结果计算非饱和状态下吸力应力σs的公式，如式(7)。

(7)

图9　关于基质吸力的吸力应力特征曲线Fig. 9　SSCCs with respect to the matric suction

图10　关于体积含水率的吸力应力特征曲线Fig. 10　SSCCs with respect to the volumetric water content

图11　关于有效饱和度的吸力应力特征曲线Fig. 11　SSCCs with respect to the effective degree of saturation

如图9～图11所示，吸力应力随湿度的降低而增大。边界效应区范围内，净围压增大时，吸力应力的增大速率逐渐升高，吸力应力特征曲线间的差异逐渐减小。过渡区范围内，吸力应力特征曲线平行或近似重合，吸力应力随状态变量变化的快慢程度不受外部荷载影响。

同时，从图9～图11可以推断，下蜀土过渡阶段3种不同形式的吸力应力特征曲线的走势相似，脱湿接近残余体积含水率时吸力应力的量级为100MPa，远远超出土的剪切强度范围。对此，赵成刚等(2013)、孙文静等(2014)通过分析水在不同状态下与土结构的相互作用，肯定了向有效应力原理中引入考虑黏粒间电-化学力受结合水状态控制这一因素的应力变量的必要性。Gouy(1910)与Chapman(1913)给出了结合水状态的描述方法。

(8)

式中，h为扩散双电层厚度； n0为结合水中离子浓度正常值，随Se减小而增大； e为单位静电荷电位； v为结合水中离子的加权离子价； D为结合水介电常数； k为玻尔兹曼常数； T为热力学温度。黏粒间电-化学力是吸引力与排斥力的合力，吸引力与排斥力均随扩散双电层厚度减小而增加，但当厚度减小到黏粒表面极小范围时，排斥力与吸引力平衡(高国瑞， 2013)，即根据式(7)计算得到的高吸力对应的吸力应力是吸引力与排斥力的代数和，而非矢量和。因此，考虑黏粒间电-化学力的吸力应力函数是分段但连续的。

(9)

(10)

3结论

(1)下蜀土的变形特性与净围压及基质吸力有关。孔隙比与净围压、基质吸力呈二元指数函数关系，反映出下蜀土的压缩性随基质吸力的增大而降低的性质，解释了压缩模量随埋藏深度减少而升高的现象。

(2)净围压使下蜀土持水能力增强，净围压与进气值呈幂函数关系。土的压缩性越高，净围压对其持水特性的影响越显著； 前期等向固结导致的压缩性降低使净围压对持水特性的影响逐渐减弱。下蜀土的进气值与净围压关系的幂函数形式，也可以较好地反映鄂西北膨胀土及粗高岭土的相应性质。

(3)外部荷载对下蜀土吸力应力特征曲线的影响是分段的。在边界效应区范围内，净围压增大时，吸力应力特征曲线间的差异逐渐减小； 在过渡区范围内，吸力应力随状态变量变化的快慢程度不受外部荷载影响。

本文仅研究了下蜀土在脱湿状态下的土水-力学特性，而干湿循环过程中下蜀土的土水-力学特性仍有待后续研究。考虑黏粒间电-化学力的吸力应力函数具体形式的确定，需要有高吸力范围的土水特征曲线量测试验与三轴剪切试验基础，同时界限有效饱和度作为分段条件的适用性还有待进一步的论证。

参考文献

CaiGQ，ZhaoCG，LiuY. 2010.Temperatureeffectsonsoil-watercharacteristiccurveofunsaturatedsoils[J].RockandSoilMechanics，31(4)： 1055～1060．

ChapmanDL. 1913.Acontributiontothetheoryofelectro-capillarity[J].PhilosophicalMagazine，25(6)： 475～481．

ElkadyTY，Al-MahbashiAM，Al-RefeaiTO. 2015.Stress-dependentsoil-watercharacteristiccurvesoflime-treatedexpansiveclay[J].JournalofMaterialsinCivilEngineering，27(3)： 1～9．

GaoGR. 1998.Thestudyofswell-shrinkbehaviourofexpansivesoilsinChina[C]∥Proceedingsof8thInternationalCongressIAEG.Rotterdam,Netherlands:AABalkema: 295～297．

GaoGR. 2013.Neotericsoilgeotechnology(secondedition)[M].Beijing：SciencePress.

GaoGR，HanAM. 2005.DistributionofregionalsoilsinChinaandformationoftheirspecialgeotechnicalproperties[J].ChineseJournalofGeotechnicalEngineering，27(5)： 511～515．

GongBW，WuHW，WangB. 2004.Influenceofstressstatesonsoil-watercharacteristicsofexpansivesoils[J].RockandSoilMechanics，25(12)： 1915～1918．

GouyG. 1910.Surlaconstitution，delachargeelectriquealasurfaced’unelectrolyte[J].AnniuePhysique，(9)： 453～468．

GuK，ShiB，TangCS. 2011.ExperimentalstudyandmechanismsofswellingpropertiesofXiashu-bentonitemixture[J].Hydrogeology&EngineeringGeology，38(4)： 125～129．

HanAM，QiaoCY，DingCY. 2009.StudyonthestructuralstrengthofXiashusoilinNanjing[J].JournalofEngineeringGeology，17(3)： 371～376．

HanAM，XiaoJH，QiaoCY，etal. 2013.ExperimentsonmicroandmacrobehaviorsofNanjingXiashusoilundertriaxialcompression[J].JournalofJilinUniversity(EarthScienceEdition)，43(6)： 1897～1903．

LuN，AsceM,LikosWJ. 2006.Suctionstresscharacteristiccurveforunsaturatedsoil[J].JournalofGeotechnicalandGeoenvironmentalEngineering，132(2)： 131～142．

LuN. 2008.Ismatricsuctionastressvariable？[J].JournalofGeotechnicalandGeoenvironmentalEngineering，134(7)： 899～905．

MatyasEL，RadhakrishnaHS. 1968.Volumechangecharacteristicsofpartiallysaturatedsoils[J].Géotechnique，18(4)： 432～448．

MeiL，JiangPM，LiP，etal. 2013.Soil-watercharacteristiccurvetestsonunsaturatedsoil[J].ChineseJournalofGeotechnicalEngineering，35(S1)： 124～128．

PhamHQ，FredlundDG. 2011.Volume-massunsaturatedsoilconstitutivemodelfordrying-wettingunderisotropicloading-unloadingconditions[J].CanadianGeotechnicalJournal，48(2)： 280～313．

PhoonKK，SantosoA，QuekST. 2010.Probabilisticanalysisofsoil-watercharacteristiccurves[J].JournalofGeotechnicalandGeoenvironmentalEngineering，136(3)： 445～455．

SunHL，ZhaoXY. 2004.ExperimentalstudyonimprovedXiashucohesivesoilforexpressrailwaysubgrades[J].ChineseJournalofGeotechnicalEngineering，26(2)： 293～295．

SunWJ，SunDA，LiuSQ，etal. 2014.Hydro-mechanicalbehaviourofGMZCa-bentoniteathighsuctions[J].ChineseJournalofGeotechnicalEngineering，36(2)： 346～353．

TanXH，YuW，ShenMF，etal. 2013.Experimentalstudyandcurvefittingofsoil-watercharacteristiccurve[J].RockandSoilMechanics，34(S2)： 51～56．

ThuTM，RahardjoH，LeongEC. 2007.Soil-watercharacteristiccurveandconsolidationbehaviorforacompactedsilt[J].CanadianGeotechnicalJournal，44(3)： 266～275．

VanGenuchtenMT. 1980.Aclosed-formequationforpredictingthehydraulicconductivityofunsaturatedsoils[J].SoilScienceSocietyofAmericaJournal，44(5)： 892～898．

WangY，ShiB，GaoL，etal. 2010.Laboratorytestsfortemperatureeffectsofclayeysoilpermeability[J].JournalofEngineeringGeology，18(3)： 351～356．

WhiteNF，DukeHR，SunadaDK，etal. 1970.Physicsofdesaturationinporousmaterials[J].JournaloftheIrrigationandDrainageDivision，96(2)： 165～191．

XiaJ，LiuZT，ChenXM. 2001.StudyoninhomogeneityofXiashuloess[J].JournalofEngineeringGeology，9(3)： 253～257．

XiaJ，HanAM. 2009.Cyclicvariabilityinmicrostructureandphysio-mechanicalpropertiesoftheXiashuLoess-palaeosolsequenceinNanjing，China[J].EngineeringGeology，104(34)： 263～268．

ZhangW，YuL，LuM，etal. 2007.MagneticpropertiesandgeochemistryoftheXiashuLoessinthepresentsubtropicalareaofChina，andtheirimplicationsforpedogenicintensity[J].EarthandPlanetaryScienceLetters，260(1)： 86～97．

ZhaoCG，LiJ，LiuY，etal. 2013.Discussiononsomefundamentalproblemsinunsaturatedsoilmechanics[J].RockandSoilMechanics，34(7)： 1825～1831．

ZhengLP，HuXF，FangXM. 2002.AreviewofthestudyontheoriginofXiashuLoessinthemiddleandlowerreachesofYangtzeRiver[J].BulletinofMineralogy，PetrologyandGeochemistry，21(1)： 54～57．

ZhouBC，KongLW，LiangWY，etal. 2015.Hydro-mechanicalcouplingeffectsonvolumechangeandwaterretentionbehaviourofunsaturatedexpansivesoilsduringcompression[J].ChineseJournalofGeotechnicalEngineering，37(4)： 629～640．

蔡国庆，赵成刚，刘艳. 2010. 非饱和土土-水特征曲线的温度效应[J]. 岩土力学，31(4)： 1055～1060．

高国瑞. 2013. 近代土质学(第二版)[M]. 北京：科学出版社．

高国瑞，韩爱民. 2005. 论中国区域性土的分布和岩土性质的形成[J]. 岩土工程学报，27(5)： 511～515．

龚壁卫，吴宏伟，王斌. 2004. 应力状态对膨胀土SWCC的影响研究[J]. 岩土力学，25(12)： 1915～1918．

顾凯，施斌，唐朝生. 2011. 下蜀土-膨润土混合土的膨胀性试验及机理研究[J]. 水文地质工程地质，38(4)： 125～129．

韩爱民，乔春元，丁长阳. 2009. 南京下蜀土结构强度研究[J]. 工程地质学报，17(3)： 371～376．

韩爱民，肖军华，乔春元，等. 2013. 三轴压缩下南京下蜀土的宏，微观性状试验[J]. 吉林大学学报(地球科学版)，43(6)： 1897～1903．

梅岭，姜朋明，李鹏，等. 2013. 非饱和土的土水特征曲线试验研究[J]. 岩土工程学报，35(S1)： 124～128．

孙宏林，赵新益. 2004. 下蜀黏土改良土填筑高速铁路基床的试验研究[J]. 岩土工程学报，26(2)： 293～295．

孙文静，孙德安，刘仕卿，等. 2014. 高吸力下高庙子钙基膨润土的土水-力学特性[J]. 岩土工程学报，36(2)： 346～353．

谭晓慧，余伟，沈梦芬，等. 2013. 土-水特征曲线的试验研究及曲线拟合[J]. 岩土力学，34(S2)： 51～56．

王媛，施斌，高磊，等. 2010. 黏性土渗透性温度效应实验研究[J]. 工程地质学报，18(3)： 351～356．

夏佳，刘子彤，陈新民. 2001. 南京下蜀黄土的非均匀性研究[J]. 工程地质学报，9(3)： 253～257．

赵成刚，李舰，刘艳，等. 2013. 非饱和土力学中几个基本问题的探讨[J]. 岩土力学，34(7)： 1825～1831．

郑乐平，胡雪峰，方小敏. 2002. 长江中下游地区下蜀黄土成因研究的回顾[J]. 矿物岩石地球化学通报，21(1)： 54～57．

周葆春，孔令伟，梁维云，等. 2015. 压缩过程中非饱和膨胀土体变特征与持水特性的水力耦合效应[J]. 岩土工程学报，37(4)： 629～640.

HYDRO-MECHANICALBEHAVIOUROFNANJINGXIASHULOESSINDESORPTIONMOISTURESTATE

HAN Aimin LI Tong XU Hongzhong

Abstract(Institute of Geotechnical Engineering， Nanjing Tech University， Nanjing210009)

Key wordsA series of water-retention tests are carried out with different net confining pressures by the modified GDS unsaturated soil testing equipment. The deformation behaviour and water-retention characteristic of Xiashu loess are analyzed. Based on the data fitting for the soil-water retention curve of Xiashu loess with the van genuchten model, the influence of net confining pressure on the suction-stress characteristic curve(SSCC) of Xiashu loess is presented. The hydro-mechanical behaviour of Nanjing Xiashu loess in desorption moisture state is systematically studied. The experimental results show that net confining pressure and matric suction have significant influence on the deformation behaviour of Xiashu loess. When the matric suction of Xiashu loess becomes higher, the compressibility tends to be lower. The binary exponential function model is put forward to forecast the exterior relations between void ratio and stress state variables. The distinctness of water-retention characteristics of Xiashu loess follows net confining pressure rise. The power function between air-entry value and net confining pressure is reached. Net confining pressure influences the water-retention characteristic of higer compressive soil more significantly. With the increase of net confining pressure, the void ratio of Xiashu loess proceeds a convergence, and the influence of net confining pressure on the water-retention characteristic has started to decline in due process. The external load on Xiashu loess affects the SSCCs piecewise. In the boundary-effect zone, with the increase of net confining pressure, the difference between SSCCs decreases gradually. In the transition zone, the variations of the differential coefficient of suction stress with the state variables is isolated from the external load. Physical meaning and calculation method of suction stress function at high suctions acquired from theory of electrical double layer are approached. The effective boundary saturation degree is proposed as the demarcation point of suction stress function．

DOI:10.13544/j.cnki.jeg.2016.02.013

* 收稿日期：2015-01-23; 收到修改稿日期： 2015-05-28.

基金项目：国家自然科学基金项目(41072217)资助.

第一作者简介：韩爱民(1963-)，男，硕士，教授，硕士生导师，主要从事区域性土的工程性质方面的教学和科研. Email: amhan@njtech.edu.cn

中图分类号：TU411

文献标识码：A