多耦合相位振子的部分测度同步及相同步

田　静, 刘　婷, 惠小强

(1.西安邮电大学 理学院， 陕西 西安 710121;　2.西安邮电大学 通信与信息工程学院， 陕西 西安 710121；3.西安邮电大学 物联网与两化融合研究院， 陕西 西安 710061)

多耦合相位振子的部分测度同步及相同步

田静1, 刘婷2, 惠小强3

(1.西安邮电大学 理学院， 陕西 西安 710121;2.西安邮电大学 通信与信息工程学院， 陕西 西安 710121；3.西安邮电大学 物联网与两化融合研究院， 陕西 西安 710061)

摘要:对耦合哈密顿系统中两耦合相位振子的HZ模型进行改进，给出多耦合相位振子改进模型,并分析改进模型的集体动力学行为。利用标准四阶龙格-库塔法求解正则方程，将其数值结果投影到子系统运动的相平面，以获取系统各运动轨道在相平面上的演化。利用数值模拟方法,分别计算出系统振子的能量、平均能量、序参量和最大李雅普诺夫指数。利用改进后的模型可以验证：耦合哈密顿系统存在部分测度同步现象，并在同步转变点附近存在分界线混沌现象；在非同步态向测度同步态转变时，系统可达完全相同步，但无法达到完全测度同步。

关键词:耦合哈密顿系统；部分测度同步；相同步

耦合哈密顿系统中的同步现象[1]作为一种协同运动是指，两个或者两个以上随时间演化的量在演化过程中保持一定的相对关系。同步现象已在自然科学、工程技术和社会科学等诸多领域中得到了应用，例如全局耦合Logistic映射[2]、混沌振子[1]、神经网络[3]以及昆虫、动物和人类不同形式的合作行为。

Hampton和Zanette在研究耦合哈密顿系统的动力学特性时，首次发现了一种弱同步形式[4]，即在相互耦合的哈密顿系统(系统动力学结构相同，而初值不同)中，存在一个和系统初始条件有关的临界耦合强度，当耦合强度大于临界耦合强度时，子系统在相平面上分享相同的相空间并拥有相同的测度。将这种集体行为定义为测度同步，该现象表现出耦合哈密顿系统所具有的一种全新集体运动形式，该现象的模型被称为HZ模型[3]。耦合φ4哈密顿系统[5]、耦合Duffing哈密顿系统[6]、Frenkel-Kontorova模型[7]以及双组分玻色-约瑟夫森结[8-11]，耦合单摆系统[12-13]已揭示了测度同步现象。随着认识的逐步深入，又发现了多个哈密顿振子的部分测度同步[14]、混沌测度同步[15]和非局域模式的测度同步[11]。从微观角度看，任何系统都属于保守系统[16]，因此搞清楚保守系统混沌运动的性质对耗散系统以及量子混沌的研究具有重要的参考价值。

本文将HZ模型改进为多耦合相位振子模型。利用标准四阶龙格-库塔法[4]数值模拟，分别给出系统在相空间的运动轨道、系统振子的能量、平均能量、序参量及最大李雅普诺夫指数，并研究反映测度同步的一些主要性质。

1模型

HZ模型是两耦合相位振子的模型[4]。现将两耦合相位振子推广到多耦合相位振子，本文以三耦合相位振子的哈密顿系统为例，该模型对应的哈密顿量为

(1)

其中θi表示单个单摆的摆角振幅，ωi表示单个单摆的角速度，c为可调的耦合强度。H事实上由Hi和Hij两部分组成，其中

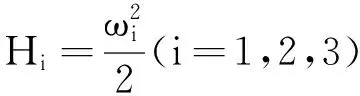
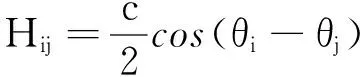
分别表示单个振子的哈密顿量和两两振子相互耦合的能量。该模型对应的动力学正则方程为

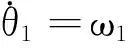
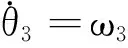
(2)

当c=0时，θi将以恒定的速度ωi增长。

2系统的部分测度同步

利用标准四阶龙格-库塔法求得正则方程的解来描述系统的动力学过程。系统的运动状态由耦合强度和初始条件决定，初始条件的值设定为

θ1(0)=0 rad,

ω1(0)=0.1 rad/s,

θ2(0)=0 rad,

ω2(0)=0.2 rad/s,

θ3(0)=0 rad,

ω3(0)=0.9 rad/s。

(3)

根据耦合强度对系统中各个振子的动力学行为的影响，将正则方程的数值结果“投影”到子系统运动的相平面(ωi-θi)上，以观察系统中的各个运动轨道在相平面上的演化。

不同耦合强度下系统各个振子的运动轨迹如图1所示。图1(a)中当c=0时，各振子的运动轨迹为相互分离的闭合曲线，即做准周期运动。随着耦合强度的增加，初始能量相近的两个振子的轨迹相互靠近。当c=0.002 6时，这两个振子的运动轨迹发生跃变，由原来的相互接近变为在相空间分享共同的区域，如图1(b)所示，它们拥有相同的测度。此时系统达到了部分测度同步即系统中一部分子系统先达到测度同步。发生跃变的那个耦合强度被称为临界耦合强度c0。随着系统的耦合强度增大，已达到部分测度同步的系统的运动轨迹出现了分界线混沌现象，系统由准周期测度同步变为混沌同步，如图1(c)所示。随后，系统又恢复到准周期的部分测度同步状态，过程分别如图1(d)至图1(f)所示。

为进一步分析系统部分测度同步相变的动力学机制以及物理特性，需要利用数值模拟方法分析部分测度同步与系统振子的能量、平均能量、序参量和最大李雅普诺夫指数等物理参量的关系。

图1不同耦合强度下HZ系统中各振子相图

2.1部分测度同步与振子能量的关系

要定量分析系统的动力学机制，尤其是部分测度同步的性质，必须借助系统的能量特性。单个振子的能量为[4]

不同耦合强度下，各振子能量随时间的变化关系，如图2所示。在图2(a)中，当c=0时，系统没有耦合，各个振子的能量稳定没有波动。在图2(b)中，当各个振子间的耦合强度增加时，能量开始随时间变化，初始能量相近的振子能量之间的差距逐步缩小。在图2(b)和图2(c)中，插图为第3个振子的能量随时演化放大图。如图2(c)所示,当耦合强度超过临界值时，两个振子的能量达到交换平衡，系统达到部分测度同步，继续增大振子的耦合强度，能量会随着时间波动变大，但依然是交换平衡状态。图2反映的过程对应着系统从分离到混合的过程，这也说明系统达到测度同步的本质是能量达到交换平衡。

图2　系统各振子能量随时间变化

2.2部分测度同步与平均能量的关系

当模型达到部分测度同步时，系统的运动是规则的。系统达到部分测度同步后从动力学的角度来描述，就是在一个振子所能达到相空间中的任意小邻域内总能找到另一个振子的运动轨道，两个子系统的相空间拥有相同的区域与测度，因此两者的长时间演化所有平均量是相等的。虽然,这些平均量相等只是测度同步的一个必要条件，但这些量能反映出系统的某些特征[16]。为描述系统达到测度同步的转变，要计算系统中单个振子的平均能量[4]

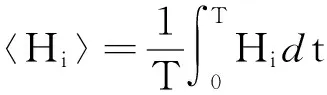
其中T为周期。

系统中振子的平均能量随耦合强度的变化关系如图3所示。可见，初始能量相近的两个振子的平均能量在临界耦合强度c0=0.002 6时发生跃变达到了能量平衡。当c0.08时单个振子的平均能量回归能量平衡同时，由图可见，非同步到同步是一个突变的过程，同步过程能在一个较长的范围内保持。这一过程说明平均能量可以定量刻画测度同步的转变。

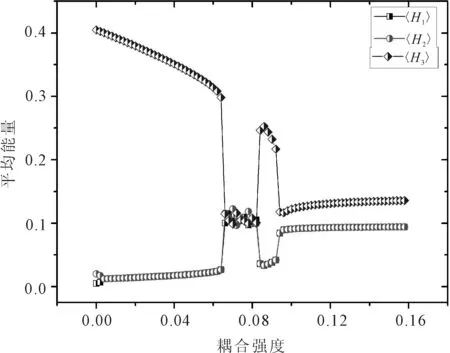
图3　系统中各振子平均能量随耦合强度变化

2.3部分测度同步与序参量的关系

为了表现部分测度同步相变过程得复杂性，通过引入序参量的概念来描述系统从非同步态向测度同步态的转变,每个子系统的轨道相平面(ωi-θi)上两个振子的相差[4]

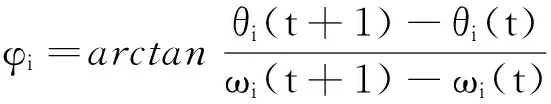
选取关于时间t的周期函数m(t),并令

φi(t+1)=φi(t+1)+2πm(t+1)。

若φi(t+1)<φi(t)，则m(t+1)=m(t)+1，否则m(t+1)=m(t)，且m(t)满足m(0)=0。因此,它可保证系统相差的单调性。单一振子在相平面的位相可表示为

φi=φi+2πm(t)，

系统在相平面的相差为

Δφ(t)=φ1(t)-φ2(t)。

测度同步达到之前，相差随时间近似成线性关系

φ(t)≈ηt+φ0。

这一关系表明不同振子轨道的主频不同。达到测度同步后，系统的相位差发生锁定，仅以一定的频率围绕某一常数振动。因此，可定义一个序参量来描述系统的动力学相变[4]，即

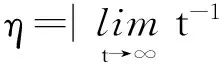
ηi,j表示振子i和振子j轨道在相平面的相差。如果ηi,j=0,则表示系统各个轨道具有相同的平均频率，代表系统已经达到相锁定。

序参量η随耦合强度变化情况如图4所示。可见，序参量在耦合强度小于临界耦合强度c0时为非零值，且随着耦合强度的增大而减小。

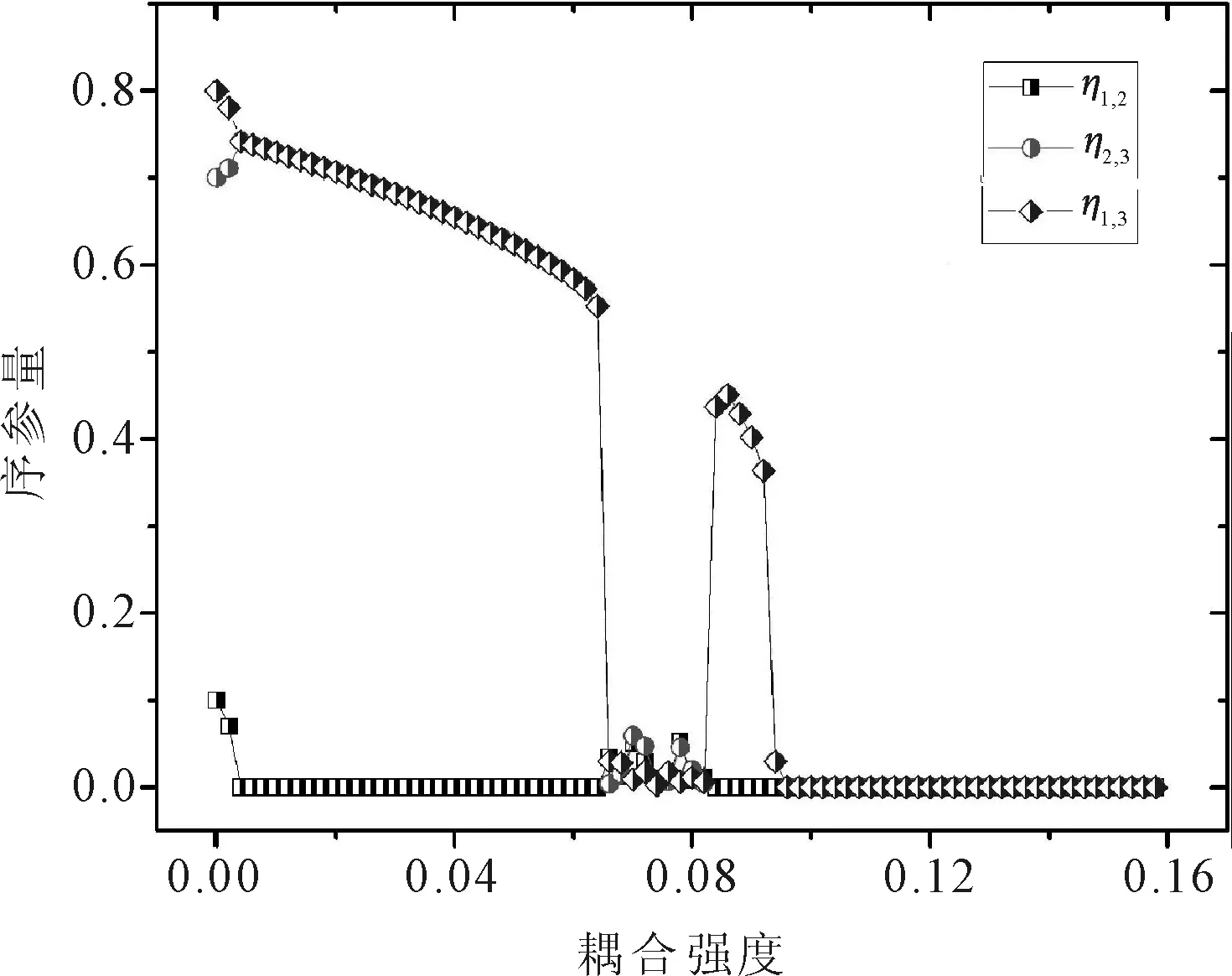
图4　序参量η随耦合强度变化

当耦合强度大于c0时，序参量降为0，表示系统有两个轨道具有相同的平均频率，相变已经发生,系统达到部分测度同步，随着耦合强度的继续增大，相差随时间的增大而增大(或减小)，最终全部变为0，此时系统所有轨道具有相同的平均频率，达到完全相同步。比较图1与图4，可见系统以规则运动的方式达到了测度同步，并且保持在一段很长的时间内，但是并没有达到完全测度同步。然而，从图4可见，在临界转变点以后，经过一段时间的演化相位差发生完全锁相，系统达到完全相同步。

在HZ系统中对四振子和五振子平均能量、序参量随耦合强度变化的计算后发现，部分测度同步现象仍然存在，说明部分测度同步现象是HZ模型的一个集团化的过程，是耦合哈密顿系统的一种普遍行为。

2.4部分测度同步与最大李雅普诺夫指数的关系

系统在转变过程中出现过混沌同步现象，为了更清晰反映这段混沌同步过程，来计算最大李雅普诺夫指数。最大李雅普诺夫指数λm与耦合强度c的关系如图5所示。

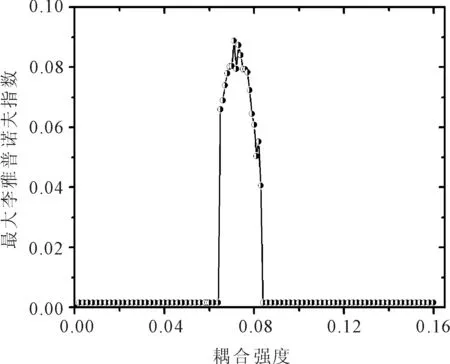
图5　最大李雅普诺夫指数与耦合强度的关系

由图5可见，系统在达到部分测度同步的过程后出现了混沌窗口，此时最大李雅普诺夫指数λm大于0，表明系统处于混沌同步状态，此现象在图1～图4中均会发现。当最大李雅普诺夫指数λm降为0时，系统恢复到准周期部分测度同步。

3结语

将两耦合的HZ模型推广到多耦合振子的哈密顿系统，对其动力学行为进行分析，发现其存在部分测度同步及相同步现象，数值计算结果表明，同步的转变点会发生分界线混沌现象，序参量和最大李雅普诺夫指数分析表明，系统从非同步态到部分测度同步态的相变过程中没有达到完全的测度同步，但达到了完全的相同步。

参考文献

[1]BENNETTAM,SCHATZMF,ROCKWOODH.Huygens’sclocks[J].ProceedingsMathematical,PhysicalandEngineeringSciences,2001,458(2019):563-579.

[2]LLOYDAL.Thecoupledlogisticmap:asimplemodelfortheeffectsofspatialheterogeneityonpopulationdynamics[J].JournalofTheoreticalBiology, 1995, 173(3): 217-230.

[3]HANSELD,SOMPOLINSKYH.Synchronizationandcomputationinachaoticneuralnetwork[J].PhysicalReviewLetters, 1992, 68(5): 718.

[4]HAMPTONA,ZANETTEDH.MeasuresynchronizationincoupledHamiltoniansystems[J].Physicalreviewletters, 1999,83(11): 2179.

[5]CHENSY,WANGGR,CHENSG.MeasureSynchronizationofHigh-CycleIsletsinCoupledHamiltonianSystems[J].ChinesePhysicsLetters, 2004, 21(11): 2128-2122.

[6]VINCENTU.MeasuresynchronizationincoupledDuffingHamiltoniansystems[J].NewJournalofPhysics, 2005, 7(1): 209-212.

[7]YANGY,WANGCL,JIANGH,etal.SynchronizationintheFrenkel-Kontorovatypesystem[J].PhysicaScripta, 2012,86(1): 015003.DOI:10.1088/0031-8949/86/01/015003.

[8]TIANJ,QIUHB,WANGGF,etal.Measuresynchronizationinatwo-speciesbosonicJosephsonjunction[J].PhysicalReviewE, 2013,88(3): 032906.

[9]TIANJ,QIUHB,CHENY.NonlocalmeasuresynchronizationincoupledbosonicJosephsonjunctions[J]ChinesePhysicsLetters, 2010, 27(7): 70501-70504.DOI：10.1088/0256-307x/2 7/7/O70501.

[10] 田静,邱海波,陈勇. 耦合哈密顿系统中测度同步发生机理的研究[J]. 物理学报, 2010, 59(6): 3763-3768.

[11] 田静. 耦合Morse振子中测度同步的研究[J]. 兰州大学学报：自然科学版, 2013(4):19-23.

[12]CHENZC,LIB,QIUHB,etal.Collectivedynamicsinanon-dissipativetwo-coupledpendulumsystem[J].ChinesePhysicsB, 2014, 23(5): 050506.DOI：10.1088/1674-1056/23/5/050506.

[13]LIB,CHENZC,QIUHB,etal.Criticalphenomenonoftwocoupledphaseoscillators[J].TheJournalofChinaUniversityofPostsandTelecommunications, 2013，20(2): 121-127.DOI: 10.1016/S1005-8885(13)60208-3.

[14]WANGXG,LIHH,HUK,etal.PartialmeasuresynchronizationinHamiltoniansystems[J].InternationalJournalofBifurcationandChaos, 2002,12(5): 1141-1148.

[15] 陈绍英, 许海波, 王光瑞, 等. 耦合哈密顿系统中测度同步的研究[J]. 物理学报, 2005, 53(12): 4098-4110.

[16] 陈绍英,顾思齐,孔祥宇. 耦合Duffing哈密顿系统的测度同步及相同步[J]. 河北师范大学学报:自然科学版, 2011,35(1):37-44.

[责任编辑:祝剑]

Partialmeasuresynchronizationandphasesynchronizationinmulti-couplingphaseoscillators

TIANJing1,LIUTing2,XIXiaoqiang3

(1.SchoolofScience,Xi’anUniversityofPostsandTelecommunications,Xi’an710121;2.SchoolofCommunicationandInformationEngineering,Xi’anUniversityofPostsandTelecommunications,Xi’an710121;3.InstituteofInternetofThingsandIT-basedIndustrialization,Xi’anUniversityofPostsandTelecommunications,Xi’an710061)

Abstract:A multi-coupling phase oscillators model is given to supersede the two-coupling phase oscillators HZ model in coupled Hamiltonian system, and its collective dynamics behavior is analyzed. The standard fourth-order Runge-Kutta method is applied to solve the canonical equation, and the numerical results are projected to the system motion phase plane to find out the evolvement of every moving track in the system on the phase plane. By using numerical simulation method, the oscillator's energy, the average energy, the order parameter and the maximum Lyapunov exponent can be figured out. By the given model, it can be elicited that, there are partial measure synchronization existing in the coupled Hamiltonian system, and separatrix chaos emerges around the synchronous transition point. The system will be completely phase synchronization when the system phase transform from non-synchronization to synchronization, but it will not reach completely measure synchronization.

Keywords:coupled Hamiltonian systems, partial measure synchronization, phase synchronization

doi:10.13682/j.issn.2095-6533.2016.02.013

收稿日期：2015-09-02

基金项目：国家自然科学基金资助项目(11104217,11402199);陕西省自然科学基金资助项目(2014JQ1022);陕西省教育厅科学研究计划资助项目(2014JK1676)

作者简介：田静(1981-)，女，博士，副教授，从事非线性动力学及其应用研究。E-mail：tianj2005@gmail.com 刘婷(1989-)，女，硕士研究生，研究方向为信号与信息处理。E-mail：742995926@qq.com

中图分类号：O321

文献标识码：A

文章编号：2095-6533(2016)02-0068-05