苏里格气田含水气藏废弃地层压力确定的新方法

郑腊年，安红燕，达丽娜，霍明会

（1.中国石油长庆油田分公司苏里格气田研究中心气藏动态研究，陕西西安　710018；2.低渗透油气田勘探开发国家工程实验室，陕西西安　710018；3.中国石油长庆油田分公司，陕西西安　710018）



苏里格气田含水气藏废弃地层压力确定的新方法

郑腊年1，2，安红燕1，2，达丽娜3，霍明会1，2

（1.中国石油长庆油田分公司苏里格气田研究中心气藏动态研究，陕西西安710018；
2.低渗透油气田勘探开发国家工程实验室，陕西西安710018；3.中国石油长庆油田分公司，陕西西安710018）

摘要：苏里格气田是典型的致密砂岩气藏，储层不但致密，非均质性强，气井产量低，且多数产水，气藏采收率低。废弃地层压力是气藏采收率的关键影响因素之一，对于不产水气藏可以通过单相二项式产能方程结合经济极限产量综合确定，但对于产水气藏废弃地层压力的确定国内外研究不多。本文针对苏里格气田产水气藏，以最小携液速度下的产气量与产水时经济极限产气量相结合共同确定了废弃产量区间范围，应用质量守恒原理推导得出气水两相产能公式，最终求取含水气藏废弃地层压力的一种新方法，并对影响因素进行分析。本文利用VC编程采用多次迭代计算，提高了计算精度，为产水气藏废弃地层压力的求取及采收率的确定提供了一种新思路。

关键词：含水气藏；二项式产能方程；废弃产量；废弃地层压力

废弃地层压力是计算气藏采收率或可采储量的重要参数，也是有关地面工程论证和设计的重要指标和依据。对于不产水气藏可以通过单相二项式产能方程结合经济极限产量综合确定［1-3］，但对于产水气藏，目前有余贝贝、唐海等［4］提出的以气井最小携液速度为约束条件，通过复合半径模型确定地层产水时气井的稳定二项式产能方程进行求取，但它存在的问题是复合半径参数求取的不确定性，以及复合半径模型不能得出不同水气比下的伤害程度，给这种方法的应用带来一定的局限性。

本文根据质量守恒原理推导出来的产水气井二项式产能方程，以多种集输条件下的气井最小携液流量和产水时经济极限产量为约束，最终获得了产水气井废弃地层压力，并对影响废弃地层压力因素进行分析。

1　含水气藏废弃地层压力确定方法

1.1废弃井口压力

自喷开采井废弃井口压力等于最低外输气压力，苏里格上古井流程外输压力为3MPa，下古井流程外输压力为6.4MPa。随着气田深入开发，在一级增压以及多级增压的情况下，气井的最小集输井口压力可低至0.5MPa。

1.2废弃井口产量

对于产水气井，随着地层压力的下降，气井最大产气量不断降低，当最大产气量低于最小携液速度下的产气量时，此时气井将不能正常生产，对应产气量即为废弃井口产量。

目前，比较常见的临界携液流量模型主要有Turner模型、李闽模型和王毅忠模型。对于苏里格气田，王毅忠模型与实际生产情况比较接近，故本文采用王毅忠模型来计算废弃井口压力下对应的临界携液流量即废弃井口产量：

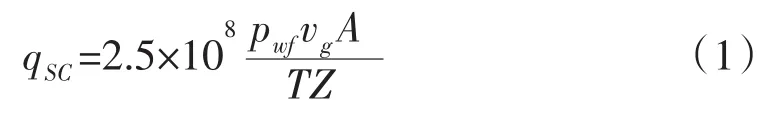
其中：

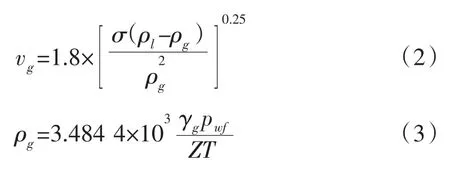
式中：qSC-最小携液产气量，m3/d；pwf-井底流动压力，MPa；vg-气体流速；A=πd2/4-油管内截面积，m2；d-油管内径，m；T-气流温度，K；Z-天然气偏差系数；σ-界面张力，对水取60 mN/m；ρl-液体密度，kg/m3，水取1 074 kg/m3；ρg-天然气密度，kg/m3；γg-天然气相对密度。

1.3废弃井底流压

已知废弃井口压力和井口产量，代入到井底流压计算公式中，便可算出废弃井底流压，其公式如下：

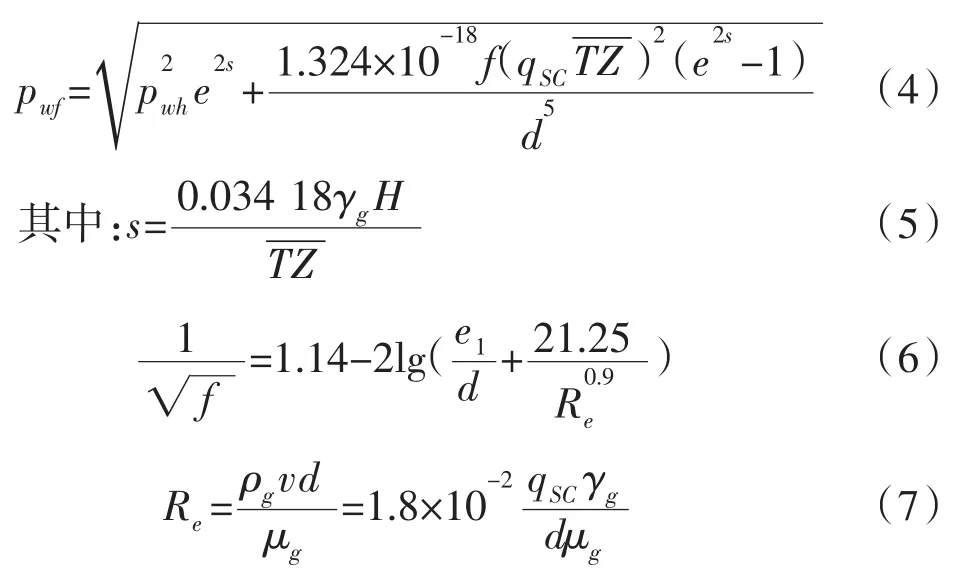
式中：pwh－井口油压，MPa；H－气层中深，m；e1－管壁粗糙度，m；μg－一定温度压力下的天然气黏度，mPa·s。

由于垂直段随着井深的变化井筒的压力和温度都会发生变化，从而引起了偏差系数和黏度的变化，为了计算更加准确，本文将垂直井段以每米为单位划分单元，每个单元计算出相应的平均偏差系数和黏度进行迭代计算。步骤如下：

（1）划分单元，确定基本参数。

（2）假设下一单元的初始压力，让它等于上一单元的压力。取它们的平均值求出本段相应的压力。

（3）根据平均压力和平均温度计算出拟压力和拟温度，进而计算出下一段的偏差系数和黏度等参数。

（4）采用式（4）求出下一段压力。

（5）用计算出来的压力跟假设的压力值作比较，若两者比较接近时，则计算出来的压力即为所求，否则将计算出的压力作为迭代值，重复步骤（2）～（4）继续计算直到满足精度为止。

（6）重复上面的步骤，直到计算到井底。

根据上述步骤，利用VC编制相应程序，从而得出气井垂直井筒压力分布曲线（见图1），从图1中可以看出井筒压力随井深呈线性增加。

图1　井筒压力随井深变化的关系曲线

1.4废弃地层压力确定方法

1.4.1产水气井产能方程的确定对于产水气井，引入气水两相拟压力函数。

同时考虑表皮系数和高速非达西渗流的影响，推导出产水气井二项式产能方程，如下式所示：

其中：

式中：ψ（p）-拟压力，kg·MPa/（m3·mPa·s）；krg-气相相对渗透率；krw-水相相对渗透率；μw-一定温度压力下的水相黏度，mPa·s；ρgsc-地面标准状况下气体密度，kg/m3；ρwsc-地面标准状况下水密度，kg/m3；WGR-水气体积流量之比，m3/m3；re-供给半径，m；rw-井口半径，m；S-表皮系数；k-储层渗透率，10-3μm2；h-气层有效厚度，m。

该产能方程中引入两相拟压力公式比用压力平方计算精度高，此外引入水气比这个参数，进而可以计算不同水气比对废弃地层压力影响。

1.4.2两相拟压力与地层压力的关系根据储层岩心气水相对渗透率曲线，可以得出两相拟压力与地层压力的关系曲线（见图2），从图2中可以看出，随着压力的增大，气水两相拟压力随之增大。

图2　两相拟压力与压力的关系曲线

1.4.3二项式产能系数与地层压力的关系从式（10）、（11）中可以看出，在气井开采过程中假设表皮系数S不变，当地层压力下降时，二项式系数A值不变，式（11）中的黏度将会发生变化从而影响B值的变化。假设气井在不同开采阶段的二项式产能系数分别为B1和B2且对应的天然气黏度分别为μg1和μg2，那么根据式（11）有：

根据上式作出二项式系数B随地层压力变化的关系曲线（见图3）。

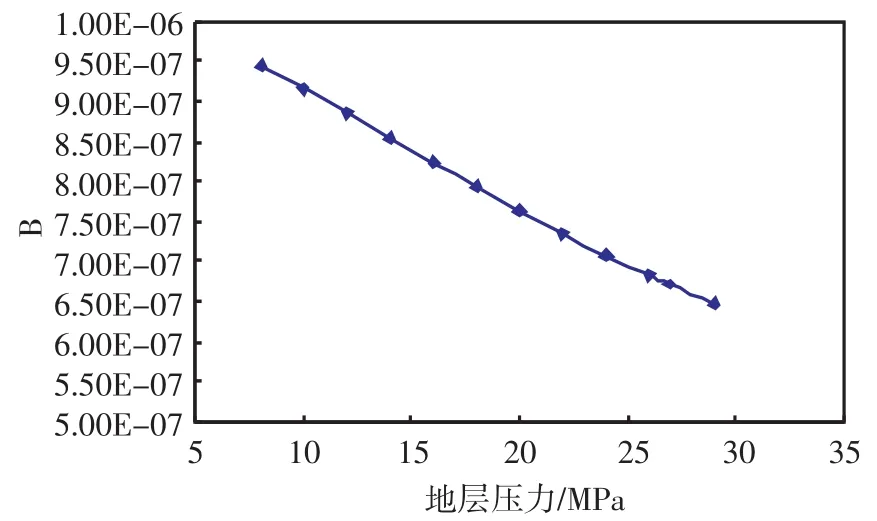
图3　B值随地层压力变化曲线

由图3知，B值随地层压力的降低逐渐增加，因此若始终采用初期建立的稳定产能方程来计算废弃地层压力必将带来误差。

1.4.4废弃地层压力计算由1.2和1.3节确定出废弃产量和废弃井底流压后，代入到二项式产能公式（9）中，从而可以求出对应的废弃地层压力。但是具体计算中存在的难点是：在求解二项式系数B时需要先得到废弃条件下的天然气黏度，而求解又需要知道废弃地层压力，然而气井的废弃地层压力本身就是需要求解的参数，是未知的，因此需要采用迭代计算方法。利用VC编制程序，求解废弃地层压力，其具体步骤为：

（1）令废弃地层压力p的初始迭代值p0为原始地层压力；

（3）按式（9）计算ψ（p），根据ψ（p）与p的关系，求出对应的p值；

（4）若计算出来的值p与假定的值p0相差很小，则计算出来的压力即为所求的废弃地层压力；否则，取p0=p，重复（2）～（3）步，直到满足要求。

2　实例应用

本文以SX区块为例，该区块渗透率介于0.06 mD～2.457 mD，平均值为0.510 mD。有效厚度介于2m～22.7m，平均值为8.6m，气层平均中部埋藏深度3 556m，原始地层压力31MPa，水气比平均为0.8m3/104m3。

考虑多种集输条件下的情况，计算出对应的临界携液流量，进而求出废弃井底流压，再利用产水气井二项式产能公式，得到产水气藏废弃地层压力，同时计算出产水经济极限产量下对应的废弃地层压力，其结果（见表1）。

表1　不同集输条件下废弃地层压力情况

从表1中可以看出，不同集输条件下，废弃地层压力差异比较大。在自然生产条件下，其临界携液流量即为其极限产量，计算出来的废弃地层压力要大于采取措施下的废弃地层压力，因此对于产水气藏废弃地层压力最小值为采取措施情况下计算的废弃地层压力值，最大值是自然生产递减到临界携液流量时对应的废弃地层压力，此压力范围对产水气藏的开发具有实际指导意义。

此外，考虑产水井需采取排水采气措施，其经营成本有所增加，计算出产水和不产水情况下对应的废弃地层压力，其结果（见表2）。

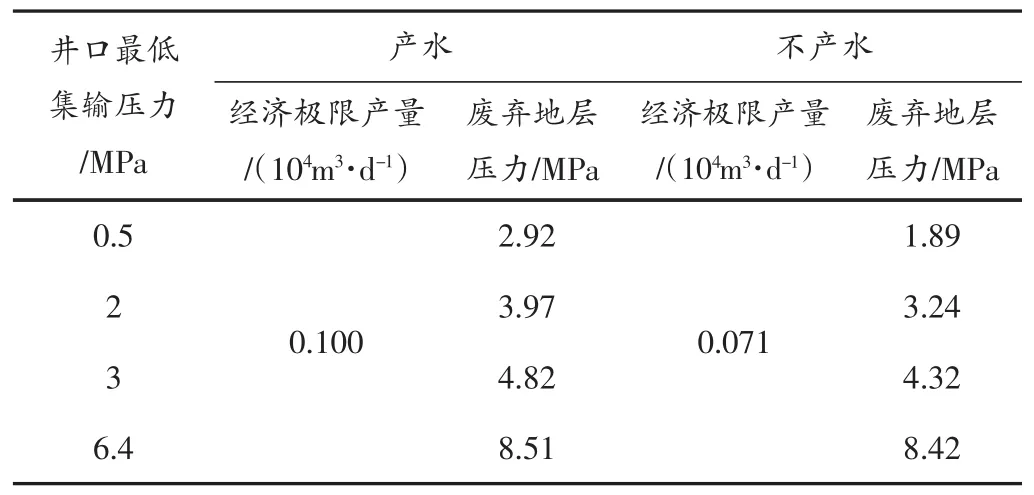
表2　产水和不产水情况下废弃地层压力对比表

从表2中可以看出，水的存在会使废弃地层压力增加，同时井口集输压力越小，水的影响越大，废弃地层压力增加的幅度也越大。因此对于产水气井废弃地层压力的计算需要采用产水气井二项式产能方程，不能用单相产能公式代替。

3　废弃地层压力影响因素分析

根据上述理论公式，结合SX区块各项基本参数，分别作出气层渗透率、有效厚度、井口最低集输压力、水气比对废弃地层压力的影响曲线（见图4～图7）。

3.1渗透率的影响

从图4可以看出，在渗透率较低时，废弃地层压力随渗透率的增加明显减小，而在渗透率较高时，废弃地层压力随渗透率的增加变化很小，有一明显分界点，即在渗透率高于0.2 mD后废弃地层压力趋于平缓。说明在低渗条件下，废弃地层压力对渗透率非常敏感，而在渗透率较高时则影响很小。

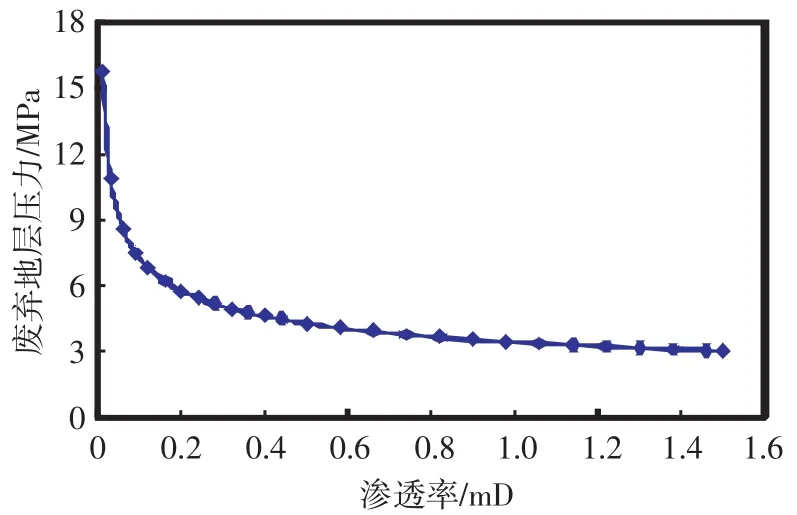
图4　渗透率对废弃地层压力的影响

3.2气层有效厚度的影响

考虑不同地层渗透率条件下有效厚度变化对废弃地层压力的影响，从图5中可以看出，随着有效厚度的增加，废弃地层压力逐渐降低。此外，当储层渗透率较低时，随有效厚度的增加，废弃地层压力降低幅度比较大；而在渗透率较高时，废弃地层压力降低的幅度较小。说明储层渗透率较低时，废弃地层压力对有效厚度比储层渗透率高时更敏感。

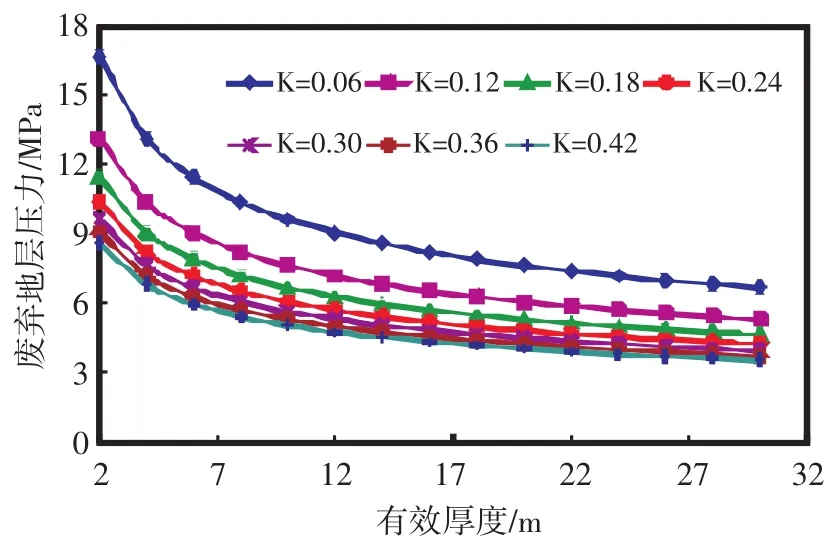
图5　有效厚度对废弃地层压力的影响

3.3井口最低集输压力的影响

不同井口最低集输压力下废弃地层压力随有效厚度变化的关系曲线，从图6中可以看出，废弃地层压力随井口最低集输压力的增加而增大。

图6　井口最低集输压力对废弃地层压力的影响

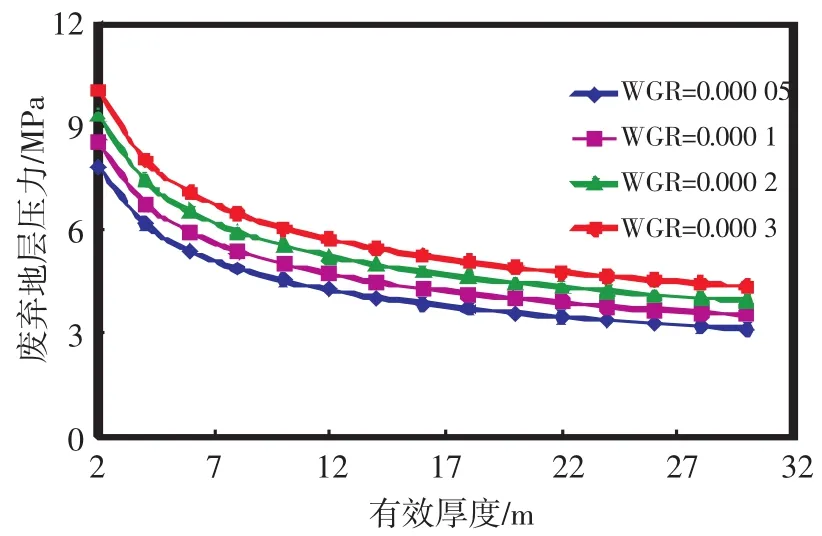
图7　水气比对废弃地层压力的影响

3.4水气比的影响

不同水气比条件下废弃地层压力随有效厚度变化的关系曲线，从图7中可以看出，废弃地层压力随水气比的增加而增大。由此可知，水的存在对废弃地层压力的影响不容忽视。

4　结论

（1）针对产水区块，在自然生产情况下，提出了以临界携液流量为极限产量，利用产水气井二项式产能方程评价废弃地层压力。该方法计算的结果大于采取措施情况下的废弃地层压力，为废弃地层压力的上限值，对产水气藏的开发有实际指导意义。

（2）随着气井地层压力的下降，二项式系数A值不变，B值不断增加，因此必需用废弃时的产能方程计算废弃地层压力。

（3）废弃地层压力随储层渗透率的增加逐渐降低，当渗透率小于0.2 mD，渗透率对废弃地层压力的影响十分明显；当渗透率大于0.2 mD，渗透率对废弃地层压力的影响不明显。

（4）废弃地层压力随有效厚度的增加而减小，且储层渗透率较低时，废弃地层压力对有效厚度比储层渗透率高时更敏感。

（5）随着井口最低集输压力和水气比的增加，废弃地层压力逐渐增大，水的存在对废弃地层压力的影响不容忽视。

参考文献：

［1］郝玉鸿，阎纪辉.确定气井废弃地层压力的新方法［J］．油气采收率技术，1999，6（4）：77-82．

［2］邹建波，李闽，代平，等．气藏废弃压力和采收率影响因素［J］.新疆石油地质，2006，27（6）：736-739．

［3］卢涛，兰义飞，何磊．一种计算气藏废弃压力的方法-二项式产能方程法［J］．天然气勘探与开发，2009，32（2）：18-20．

［4］余贝贝，唐海，李东林，等．产水气藏废弃压力的确定方法［J］．新疆石油地质，2008，29（5）：641-643.

A new model of determination of abandonment pressure in water bearing gas reservoir in Sulige gasfield

ZHENG Lanian1，2，AN Hongyan1，2，DA Lina3，HUO Minghui1，2
（1.Sulige Gasfield Research Center of PetroChina Changqing Oilfield Company，Xi'an Shanxi 710018，China；2.National Engineering Laboratory for Exploration & Development of Low-Permeability Oil & Gasfield，Xi'an Shanxi 710018，China 3.PetroChina Changqing Oilfield Company，Xi'an Shanxi 710018，China）

Abstract:Sulige gasfield is typical of tight sandstone gas reservoirs. The reservoir not only compact，strong heterogeneity，low gas production，and high water production. The gas reservoir recovery has many factors. Abandonment formation pressure is one of the key factors that influence gas reservoir recovery. For no water gas reservoir can be integrated to determine by single-phase binomial productivity equation combined economic output limit，but for producing water gas reservoir，research of abandonment formation pressure is not much. For Sulige gasfield，this paper proposed a new method for calculating abandonment formation pressure，which used gas water two phase productivity formula derived from principle of mass conservation and combine with abandonment gas production rate range by determined by gas production at the minimum liquid carring rate and economic limit production of waterproduction. To improve accuracy，we use VC programming using multiple iterative calculations. This paper provides a new idea for caculating water gas reservoir abandonment formation pressure and recovery.

Key words：water bearing gas reservoir；binomial deliverability equation；abandonment production rate；abandonment formation pressure

中图分类号：TE377

文献标识码：A

文章编号：1673-5285（2016）06-0075-05

DOI:10.3969/j.issn.1673-5285.2016.06.019

*收稿日期：2016－05-16

作者简介：郑腊年（1986-），2013年毕业于西南石油大学油气田开发工程专业，现在长庆油田苏里格气田研究中心工作，从事气藏工程方面的研究工作，邮箱：zln.0404@163.com。