多因素作用下复杂系统多级可拓关联预测模型及应用

陆　慧

(安徽财贸职业学院， 合肥 230601)



多因素作用下复杂系统多级可拓关联预测模型及应用

陆慧

(安徽财贸职业学院， 合肥 230601)

摘要：针对复杂系统预测分析的问题，提出一种多因素作用下的复杂系统多级可拓关联预测模型。首先建立预测对象的关联指标以及可拓类别，确立不同可拓类别下关联指标的经典域与节域，然后对关联指标进行统一化处理；建立关联预测的可拓关联函数和关联度模型，基于关联度的大小获得预测对象的归属类别。针对单次可拓关联预测结果不理想问题，通过多级细分可拓类别，最终获得精确度较高的预测结果。

关键词：可拓关联分析； 复杂系统； 多层级预测模型； 可拓理论； 多因素决策

复杂系统的预测分析是一项复杂的系统工程，需要综合考虑多方面的影响因素。这些因素往往具有模糊性、耦合性、非线性、动态性以及冗余性等特征，因此，有效、合理地确立不同影响因素与预测对象间的关联性，并基于这种关联性确立出有效的预测对象发展态势，具有十分重要的工程应用价值[1-3]。学者们从不同角度进行了研究分析，取得了一系列研究成果和较好的工程应用效果[4-8]。然而，目前的预测分析方法往往需要建立严谨的数学模型，或者需要大量有效的数据进行驱动，或者基于大量的知识进行推理。这些方法在处理具有强耦合、隐关联等特点的预测分析时，还存在一些局限性。本次研究将结合可拓理论对复杂系统的多因素预测分析进行研究，利用可拓理论中相关的方法和模型解决多因素关联预测分析过程中存在的问题，建立多因素作用下的复杂系统多级可拓关联预测模型。

1可拓理论基本概念

可拓学是我国学者蔡文教授首先提出的一门以矛盾问题为研究对象，以矛盾问题的智能化处理为主要研究内容，以可拓方法论为主要研究方法的新兴学科。它采用基元对研究对象的质和量进行结合的形式化建模，克服了数学模型只研究数量关系的局限性，以定性和定量相结合的方式描述研究对象的性质变换过程。其在各工程领域中得到了广泛的应用，并取得了一系列的工程应用成果[9-12]。基元模型和可拓距是可拓学中的2个重要工具。基元模型作为可拓学的逻辑细胞之一，通过一个有序的三元组R对分析对象进行描述。

R=(N,c,v)

(1)

式中：N —— 分析对象的名称；

c —— 分析对象的设计特征；

v —— 设计特征c的量值。

若分析对象N含有多个设计特征cj，则其基元模型为多维可拓模型，即：

(2)

式中：n —— 分析对象N的设计特征数；

vj—— cj的量值。

可拓距是可拓学中定量化分析问题的工具。若分析对象N关于设计特征cj的量值为vj，则其在参考对象的目标区间V=[va,vb]的可拓距ρ为：

(3)

2可拓关联预测模型

2.1可拓预测关联指标

由于因素的关联性，使得分析对象的预测结果受到多种因素的影响，其可拓关联预测形式可以表述为：

((c1(l)∪…∪cj(l)∪…∪cn(l))⊆Ω)

⟹[co⊆Ω]

(4)

其中：cj(l) —— 关联指标；

Ω —— 预测分析的论域；

co—— 目标预测对象；

⟹ —— 可拓关联挖掘。

从式(4)可以看出，若要有效地预测分析论域中的co，需要合理地建立与预测对象有关联关系的关联指标。因此，在遵循科学性、客观性、全面性以及系统性等原则下，借助相关统计分析或者聚类分析等方法进行关联指标的选取，从而形成可拓预测关联分析的指标集C，即：

C={c1(l),…,cj(l),…,cn(l)}

(5)

2.2可拓分类的经典域和节域

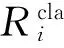
(6)

则

(7)

2.3关联指标的统一标度

(8)

若设计特征cj为效益型设计特征，则规范化后的经典域uij为：

(9)

2.4关联指标权重

不同关联指标对预测结果的贡献程度并不相同，为此对关联指标的权重进行分配。本次研究采用AHP法实现关联指标的权重分配。评判专家采取1 — 9的比率标度对关联指标进行对比打分，获得关联指标权重分配的评判矩阵A：

A=[aij]n×n

(10)

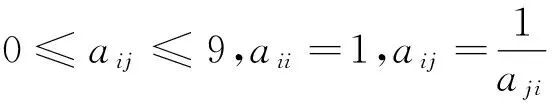
由此，获得关联指标ci的权重wi：

(11)

为判断关联指标权重分配的有效性，需进行一致性检验，即一致性比率参数CR需满足：

表1　关联指标的评判量值与含义

CR=(λmax-n)(RI×(n-1))≤0.1

(12)

式中：λmax—— 评判矩阵A的最大特征根；

RI—— 随机一次性指标，其值可通过查表获得。

当满足式(12)时，关联指标权重分配有效，否则需要对评判矩阵进行重新评判，直到获得满足一致性要求的关联指标权重为止。

2.5可拓关联函数与可拓关联度

(13)

(14)

(15)

(16)

(17)

2.6多级可拓关联预测分析

根据加权可拓关联度ψi的大小，获得预测分析对象N多因素可拓关联预测分析的择近原则，即若：

ψ0=max(ψ1,ψ2,…,ψm)=ψk

(18)

则称预测分析对象N归属于可拓类别k。根据可拓类别k对应的量值区间确定预测分析对象N的归属区间。

3应用实例

城市供水量受城市工业、附属产业以及城市人口等多因素的制约。由于水资源的逐渐匮乏和资源节约意识的提升，城市用水既要满足城市工业和附属产业发展以及人们工作生活的需要，又不能铺张浪费，因此，为了保证城市的正常运转和发展，需对城市的供水情况进行较为精确的预测。由于城市工业、附属业的发展以及城市人口都具有动态性，使得城市供水量预测具有多因素和时变性的特点。利用多因素作用下复杂系统多级可拓关联预测模型对城市供水量预测进行验证和分析。首先将三大产业的产能和城市人口数量作为城市供水量的影响因素，为了使得所有影响因素和供水量具有统一标度，选取增长率作为对应的可拓关联指标，由此获得初始的预测数据，结果见表2。

根据可拓距计算模型和可拓关联函数模型，获得预测对象与3类可拓类别之间的可拓距和关联系数，具体结果见表3。

基于AHP法获得的权重序列w=(0.154,0.477,0.288,0.801)，预测对象的可拓关联度序列ψ=(0.114,0.162,-0.271)。可以看出，预测对象归属于可拓类别N2，其对应的供水量增长率介于0.18～0.28。根据实测数据，2014年供水量的实际增长率为0.273，证明预测结果有效。

4结语

为了解决复杂系统多因素关联预测分析过程中存在的问题，对复杂系统多因素关联预测分析的模型和算法进行了探讨，给出了一种基于可拓理论的多因素作用下的复杂系统多级可拓关联预测模型。在建立预测对象可拓类别的基础上，利用可拓关联函数和可拓关联度计算模型获得预测对象的归属类别，并由此确定预测对象的预测结果。同时，通过对预测对象可拓类别的多级细化，使得预测结果更加精确和可靠。该模型物理意义明确，计算过程简单，预测适应性较好，为复杂系统预测分析工作的实施提供了新的解决途径。

表3　可拓距与关联系数

参考文献

[1] 孙强，岳继光.基于不确定性的故障预测方法综述[J].控制与决策,2014(5):769-778.

[2] 郭建英，孙永全，于春雨，等.复杂机电系统可靠性预测的若干理论与方法[J].机械工程学报,2014,50(14):1-13.

[3] 李萍，曾令可，税安泽，等.基于MATLAB的BP神经网络预测系统的设计[J].计算机应用与软件,2008,25(4):149-150.

[4] SHAO J Y, XU M Q, WANG R X. Bayesian Model-Based Fault Diagnosis for the Rotor[J]. Aircraft Engineering and Aerospace Technology, 2009, 81(1)：19-24.

[5] 李洪涛，马志勇，芮晓明.基于数值天气预报的风能预测系统[J].中国电力,2012,45(2):64-68.

[6] 苏博，刘鲁，杨方廷.GM(1,N)灰色系统与BP神经网络方法的粮食产量预测比较研究[J].中国农业大学学报,2006,11(4):99-104.

[7] 阎馨,付华.基于案例推理和数据融合的煤与瓦斯突出预测[J].东南大学学报(自然科学版)，2011,41(增刊1):59-63.

[8] 周德新，谢晓敏.基于可拓规则的故障诊断专家系统推理机的研究[J].计算机测量与控制,2011,19(2):266-268.

[9] 蔡文,杨春燕.可拓学的基础理论与方法体系[J].科学通报,2013,58(13):1190-1199.

[10] 王体春,杨爱军,卜良峰.基于多属性可拓灰关联决策模型的产品方案设计[J].系统工程理论与实践，2013,33(9):2321-2329.

[11] WANG T C, YANG A J, ZHONG S S. Multi-Attribute Extension Fuzzy Optimized Decision-Making Model of Scheme Design[J]. Tehnicki Vjesnik, 2014,21(2):239-247.

[12] CHAO K H, CHEN J W, State-of-Health Estimator Based-on Extension Theory with a Learning Mechanism for Lead-Acid Batteries [ J ]. Expert Systems with Applications, 2011, 38(12): 15183-15193.

A Multilevel Extension Association Prediction Model of Complex Systems under the Influence of Many Factors and Its Application

LUHui

(Anhui Finance & Trade Vocational College, Hefei 230601, China)

Abstract:For the problem of complex system prediction analysis, a multi-level correlation forecasting analysis model under the influence of many factors was proposed in this paper. Firstly, the correlation index and the extension category of the forecasting object were established, as well as the extension of the classical domain and the extension section of the prediction object. And the correlation index of the non uniform dimension was unified to set up a calculation model of the extension correlation function and the calculation model of the extension degree of the multi- factor correlation was achieved. On the basis of the above, the category of the forecast object was got. If the prediction results of the single extension association are not satisfactory, the extension category can be subdivided in many times, and the result of higher accuracy can be obtained.

Key words:extension association analysis; complex system; multi-level forecast model; extension theory; multi- factor decision

收稿日期：2016-01-12

基金项目：高等学校博士学科点专项科研基金项目“面向多品种部件的传送带给料加工站的在线优化控制方法”(20130111110007)

作者简介：陆慧(1982 — ),女，安徽亳州人，硕士，讲师，研究方向为数据挖掘、知识工程及人工智能。

中图分类号：TP301

文献标识码：A

文章编号：1673-1980(2016)03-0107-05