基于评价函数的空中机器人路径规划方法
董慧芬,靳雅博
(中国民航大学 机器人研究所,天津 300300)
基于评价函数的空中机器人路径规划方法
董慧芬,靳雅博
(中国民航大学 机器人研究所,天津 300300)
摘要:提出了一种基于评价函数的空中机器人路径规划方法.对空中机器人建立了二维平面内的简化动力学模型.将机器人到目标直线的路径分解为等时间间隔的序列,以机器人与目标直线的距离、角度差、速度矢量差为组成成分设计了评价函数,对每个时间间隔搜索使评价函数最小的控制量,得到最优控制量序列.进行了不同初始偏航角下的路径规划仿真实验,其结果证明了方法的有效性,达到了理想的效果.
关键词:空中机器人;路径规划;评价函数
路径规划是机器人自主导航的关键环节之一,它是指机器人在特定的的环境中,按照特定的评价标准,寻找一条从起始地点到目标状态的最优路径的过程[1].相对于传统地面机器人,空中机器人由于其飞行状态的不稳定性等种种条件限制,很难精确跟踪规划的路径.
室内微小型空中机器人的技术正方兴未艾,但目前仍然处于科学研究阶段,还没有在实际应用中投入使用.国外有宾夕法尼亚大学[2]、佐治亚理工学院[3]、瑞士苏黎世理工学院[4]都在进行室内空
中机器人自主导航的研究.国内的浙江大学、国防科技大学、北京航空航天大学、清华大学也在进行着小型空中机器人室内自主导航、路径规划的研究.
本文着重于空中机器人在起始点与目标直线已知的情况下,根据空中机器人的动力学特性对其进行建模,在充分解耦、简化的控制量基础上,进行控制量序列的求解,实现空中机器人从一点平缓飞入一条直线的最优路径的规划.
1空中机器人简化动力学模型的建立
选用Parrot AR.Drone 2.0 飞行器作为空中机器人平台,首先根据其特性建立其简化动力学模型.AR.Drone 2.0是由法国派诺特公司于2012年5月发布的飞行器,外观如图1所示.作为一款成熟的商业飞行器,它具有稳定的飞行特性,并可通过官方提供的SDK进行二次开发.通过AR.Drone2.0的SDK可以看到,AR.Drone2.0在空间运动上提供4个控制量,通过设定飞行器的水平倾角、前后倾角、垂直速度、角速度来分别控制飞行器的俯仰、滚转、高度与偏航[5],如表1所示.

图1 AR.Drone2.0飞行器
由于AR.Drone2.0良好的飞行控制特性,对其建模可以不必按照一般四旋翼飞行器的建模方式来进行.四旋翼飞行器的传统建模方式涉及到空间三个方向的位移、速度、加速度,还有三轴的角度、角速度、角加速度,总共有18个输出量,输入量一般为有4个电机的电压.并且在角加速度上还需要考虑转动惯量,这使得模型变得复杂,计算量大.并且由于飞行器的一些变量难以精确测量,故仿真效果与实际情况差距比较大.而对于AR.Drone2.0,可以根据4个控制量对飞行器飞行产生的影响来分别对4个通道进行建模.本文只研究二维平面下机器人的路径规划问题,相当于空中机器人保持一定高度飞行的前提下对飞行器在二维平面内的位置进行规划,故只对俯仰通道、滚转通道与偏航通道建模.

表1 AR.Drone2.0 SDK提供的飞行器的控制方式
在俯仰通道、滚转通道上,左/右倾角、前/后倾角与水平方向加速度之间是正相关的,在这里可以将其简化为一个线性关系,即:
ap=kθ
其中:θ为左/右或前/后方向的倾角,ap为该方向上的水平加速度,k为两者之间的比值.
AR.Drone2.0 内部设置有飞行器的最大倾角θmax,由此飞行器在水平方向上也存在一个最大的水平加速度apmax.而在实际飞行过程中,由于飞行器硬件限制,飞行器水平移动的过程中,会存在一个最大的水平速度vmax,达到vmax时飞行器会保持此速度飞行.
AR.Drone2.0通过下视摄像头拍摄图像估算飞行器的水平速度,由此实现水平方向的闭环控制,这也是 AR.Drone2.0 可以自主悬停、修正水平面内位置漂移的原因.因此,当水平方向俯仰和滚转的控制信号停止发送之后,飞行器会有减速至静止的过程,不会随惯性继续运动.设此减速过程的加速度为af.
在偏航通道上,AR.Drone2.0 SDK所提供的控制量旋转角速度为固定值ω0,作用时间t时刻后空中机器人偏航角Ψ=Ψ0+ω0t,其中Ψ0为初始时刻偏航角.
建立二维平面坐标系,如图2所示,xcOyc为平面世界坐标系,xOy为平面机体坐标系.设机体坐标系下x,y方向的速度分别为vx,vy.假设水平x方向上倾角的作用时间为tc,t时刻与t+tc时刻速度
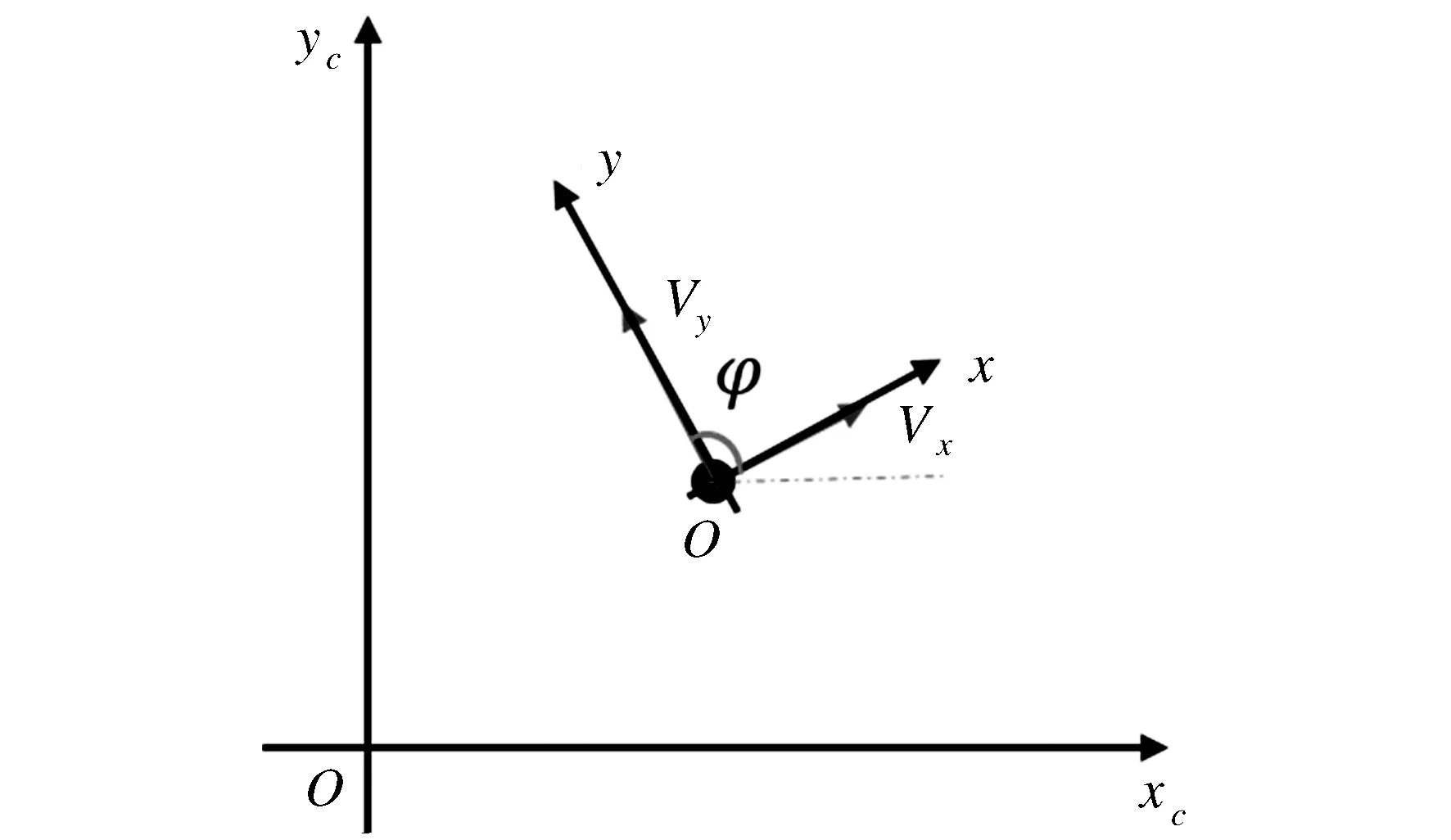
图2 二维平面世界坐标系和机体坐标系
的关系为:
假设在x方向有速度vy,在x方向没有倾角作用下,t时刻与t+tc时刻速度的关系为:
其中sign()为符号函数,定义如下:
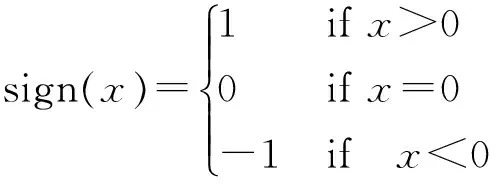
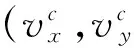
2路径规划
空中机器人的路径规划示意图如图3所示,平面上一条直线L:ax+by+c=0,空中机器人A处在直线外的一点.要求A以尽量靠近直线矢量L=(-b,a)矢量的方向来进入直线L的轨迹.
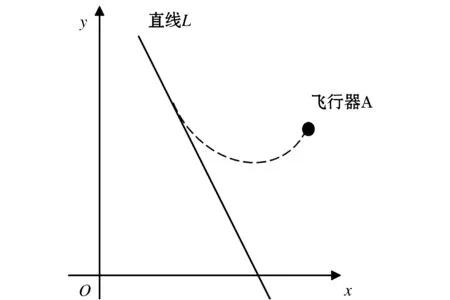
图3 路径规划示意图
2.1路径分解
将路径分解为一个由多个小的时间间隔tc组成的序列,在每一个tc内,空中机器人仅受前倾角、后倾角、左倾角、右倾角、旋转5个控制量中的一个控制,这5个控制量对空中机器人产生的影响因素如表2所示,其中Ψ0为每一次偏航角改变的量,符号由偏航角与直线矢量L=(-b,a)的夹角决定.
在每一个时间间隔的开头,都会预先计算5个控制量的作用下,这个时间间隔末尾空中机器人的状态,从中选择一个最优的控制量作为这一个时间间隔的控制量.在判断哪一个控制量最优的问题上,引入了评价函数.

表2 5个控制量对空中机器人的作用因素
2.2评价函数的设计
空中机器人在一个时间间隔的状态决定了下一个时间间隔控制量的选择,所以评价函数中应该包含空中机器人状态的因素.
2.2.1距离因素
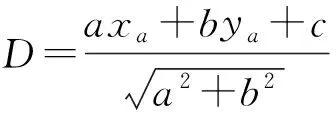
2.2.2角度因素
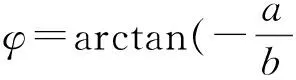
2.2.3速度矢量因素
将以上三个因素加权求和,得到评价函数:
f=αD+βΔ +γS
其中:α、β、γ为评价函数的调节系数.在每一个时间间隔的开始,分别计算五个控制量之下的评价函数fn,n=1,2,3,4,5,找到fm=min(fn),m即为对应的控制量.
2.3对旋转控制量的调整
表2中,当选择5号偏航通道的旋转控制量时,每个tc内偏航角的改变量为Ψ0.考虑到随着空中机器人的偏航角与直线方向矢量之间的角度逐渐减小,每次调整ψ0可能会使得空中机器人的偏航角始终无法靠近直线的方向.故将Ψ0修改为eΨ0,当Δ=Ψ-φ>Ψ0时,e=1;当Δ=Ψ-φ≤Ψ0时,e=1/5.
3仿真实验
设动力加速度ap=0.3 m/s2,阻力加速度af=0.15 m/s2,机体每一次转弯的角度Ψ0=8°,空中机器人在x、y方向上的最大速度vmax=1 m/s,初始速度为0,评价函数的参数α=8,β=2,γ=30.直线L:3x+y-16=0.直线的方向向量选择为(-1,3).空中机器人的初始位置点为(10,10),分别对初始偏航角为90°和180°时进行空中机器人路径规划仿真实验.
实验结果如图4, 5所示.由图4(A)和图5(A)可以看到在两个不同的初始偏航角条件下,均可得到一条路径使得空中机器人平缓飞入直线.
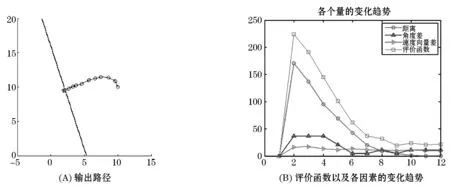
图4 初始偏航角为90°的路径规划
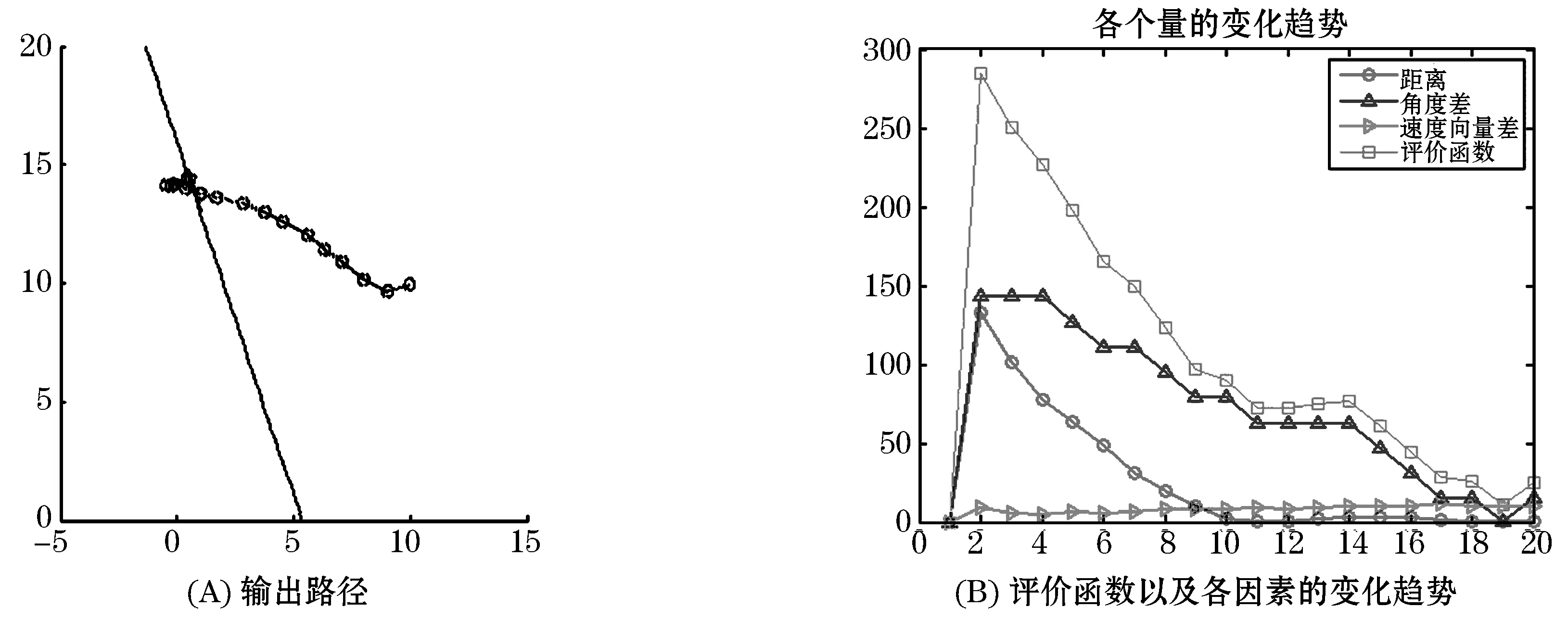
图5 初始偏航角为180°的路径规划
由图4(B)和图5(B)可以看到,90°初始偏航角条件下空中机器人用了12个时间间隔达到相对稳定,180°初始偏航角条件下空中机器人用了20个时间间隔达到相对稳定.两者的评价函数、距离、角度差、速度矢量差都呈下降趋势.说明这三个因素在评价函数中起到了作用,而在评价函数的指导下,可以规划出一条飞行器切入直线的最佳路径.
4结语
本文针对以四旋翼飞行器为实际载体的空中机器人空间路径规划问题,提出了一种基于评价函数的路径规划方法.以AR.Drone2.0飞行器为原型建立了空中机器人的简化动力学模型,通过分析机器人与直线相对位置关系中的关键三个因素设
计了评价函数.对不同初始偏航角条件进行了路径规划的仿真实验,证明了在评价函数作用下,可以规划出一条空中机器人切入直线的最佳路径,达到了预期的目的.
参考文献:
[1]何雨枫. 室内微小型无人机路径规划算法研究[D]. 南京: 南京航空航天大学, 2014.
[2]JONATHAN F, NATHAN M, SOONKYUM K. Planning and control for cooperative manipulation and transportation with aerial robots [J]. The International Journal of Robotics Research, 2011, 30(3): 324-334.
[3]SOBERS D. Indoor Navigation for Unmanned Aerial Vehicles [J]. Georgia Institute of Technology, 2009 (Feb): 1884-1889.
[4]WEISS S, SCARAMUZZA D, SIEGWART R. Monocular-slam-based navigation for autonomous micro helicopters in gps-denied environments [J]. Journal of Field Robotics, 2011, 28(6): 854-874.
[5]BRISTEAU P J, CALLOU F, VISSIERE D,etal. The navigation and control technology inside the ar. drone micro uav[C]//Milano: 18th IFAC World Congress, 2011. 1477-1484.
Aerial robot path planning method based on evaluation function
DONG Hui-fen, JIN Ya-bo
(Institute of Robotics, Civil Aviation University of China, Tianjin 300300, China)
Abstract:A path planning method based on evaluation function was proposed for aerial robot. A two-dimentional dynamics model was built for aerial robot. The path from the robot towards the target line was divided into equal time intervals sequence. An evaluation function that contains the distance, angle difference and velocity vector difference was designed. The control value that minimizes the evaluation function for every time intervals was searched so that the optimal control value sequence was obtained. The simulation experiments of path planning on different initial yaws were conducted. The result proved that the method was effective and could achieve the ideal effect.
Key words:aerial robot; path planning; evaluation function
收稿日期:2015-06-04.
作者简介:董慧芬(1970-),女,博士,副教授,研究方向:电力电子及机器人智能控制.
中图分类号:TP391
文献标识码:A
文章编号:1672-0946(2016)03-0286-04

