船用LNG储罐的液体晃荡数值分析

何晓聪，何　荣

(1.中国船级社 舟山办事处，浙江 舟山 316000； 2.浙江欣海船舶设计研究院有限公司，浙江 舟山 316000)

船用LNG储罐的液体晃荡数值分析

何晓聪1，何荣2

(1.中国船级社 舟山办事处，浙江 舟山 316000； 2.浙江欣海船舶设计研究院有限公司，浙江 舟山 316000)

摘要：针对船用LNG储罐罐内充装度不足，船舶的运动会诱发罐内LNG液体晃荡的问题，提出LNG储罐晃荡分析的VOF方法，验证模型的可用性，进行LNG储罐中液体晃荡的数值模拟，分析充装率、防波板等因素对晃荡过程的影响。研究表明，液体晃动对储罐产生的最大冲击力随充装率的升高先增大后下降，安装防波板对于15 m3小型储罐可达到较好的防波效果。

关键词：LNG储罐；液体晃荡；数值分析；防波板；充装率

船用LNG储罐属于移动容器，如果罐内充装度不足，则船舶的运动会诱发罐内LNG液体的晃荡。在恶劣工况下，激烈晃荡可对罐体产生很大的冲击力，并会对罐体与船体的连接结构造成冲击影响[1]。对于LNG储罐来说，罐内充装度不断减少，当充装度处于某一范围时，会导致晃荡问题变得更加突出。减小液体晃荡的有效途径是设置防波板，但目前国内尚未有针对船用LNG储罐防波板设置的规范或标准。通常，防波板设置过多会引入过多焊缝，从而使得结构存在焊接缺陷、焊接变形等的可能性增大，进而加大了罐体失效的风险。如果防波板脱落，将随着液体一同晃荡，从而损坏结构部件和内部管系。此外，防波板设置过多还会增加不必要的制造成本，导致空罐质量增大，降低使用效率。目前，国内外其他行业的标准、规范对移动容器防波板的设置有部分技术要求[2]，但各种规范和标准中对防波板的设置要求并不一致。船用LNG储罐是否可以参照上述各规范、标准来执行，防波板的数量对液体晃荡的影响如何，都需要深入研究。因此，有必要开展液体晃荡对船用LNG储罐的影响分析以及防波板的布置形式研究。

数值模拟是分析液体晃荡的常用方法。液体晃荡与一般的液体数值模拟的最主要区别在于其带有自由液面。目前可用于研究自由液面的数值方法主要有：MAC法、ALE有限元法和VOF法。其中，MAC法将流体的速度及压力当作求解变量，对计算机的内存空间要求高，常用于分析二维问题。ALE有限元法在某种程度上化解了非线性对流项与单元畸变间的对立，但在对每个步长进行求解时，均需确定网格速度并更新网格，计算量较大[3]。与前两种方法相比，VOF存储量明显减少，求解方法更为简单高效，更适用于三维计算。VOF方法通过定义流体体积函数F，利用其平均值表示某单元内液体的体积百分比[4]，既解决了自由液面的跟踪问题，又能够描述液面的破碎，在工程实际中取得了满意的计算结果[5]。因此采用ANSYS FLUENT软件中的VOF模型，研究储罐内的液体晃荡和防波板的设置问题。

1VOF模型的适用性分析

对于平封头型卧式容器内部介质的晃动问题，已有学者进行过数值研究，建立了平动激励下的贮箱内部液体的受迫晃动方程，提出了其等效力学模型，同时研究了液体纵向晃动的固有频率随贮箱长度、液位高度和柱体半径的变化规律。液体纵向晃动的固有频率跟柱体长度与柱体半径比值(L/R)及液位高度与柱体半径比值(h/R)的关系见图1所示[6]，考虑采用此数据与数值模拟结果对比。

图1　卧式圆柱容器内介质纵向晃动固有频率

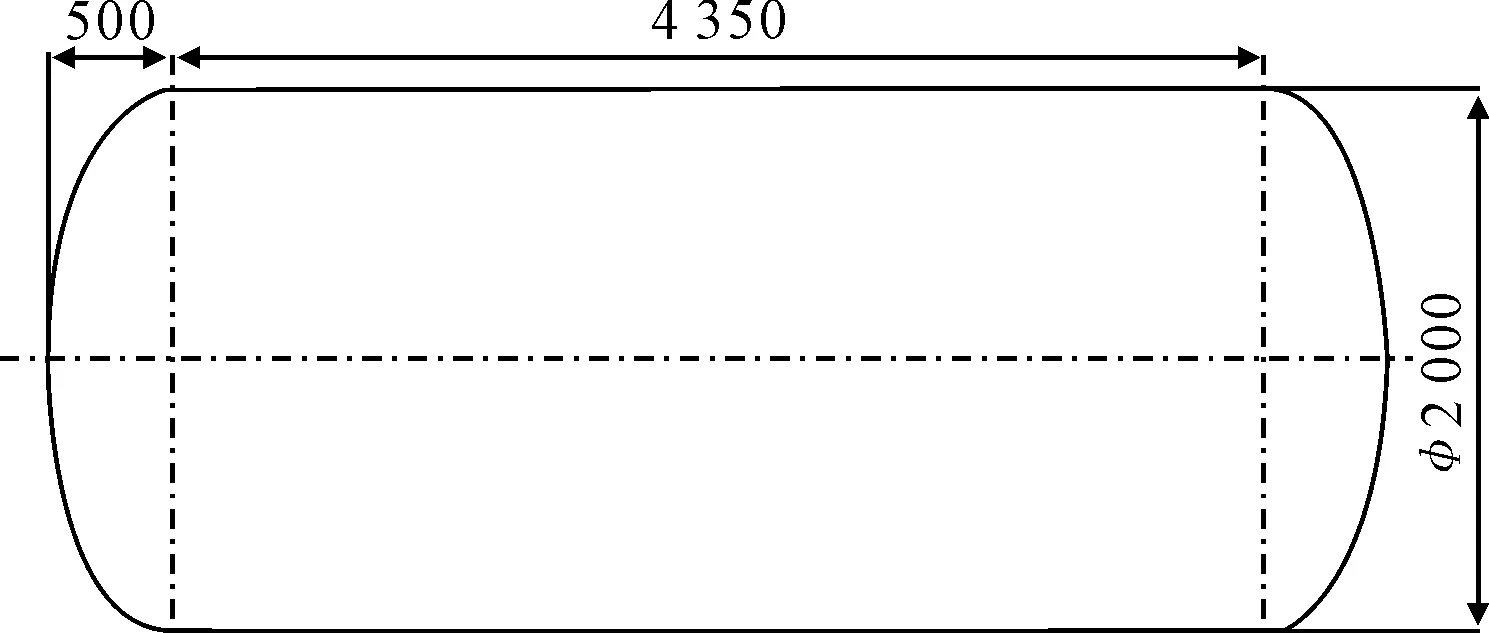
图2　LNG储罐的几何尺寸

某15 m3LNG储罐的几何尺寸见图2。

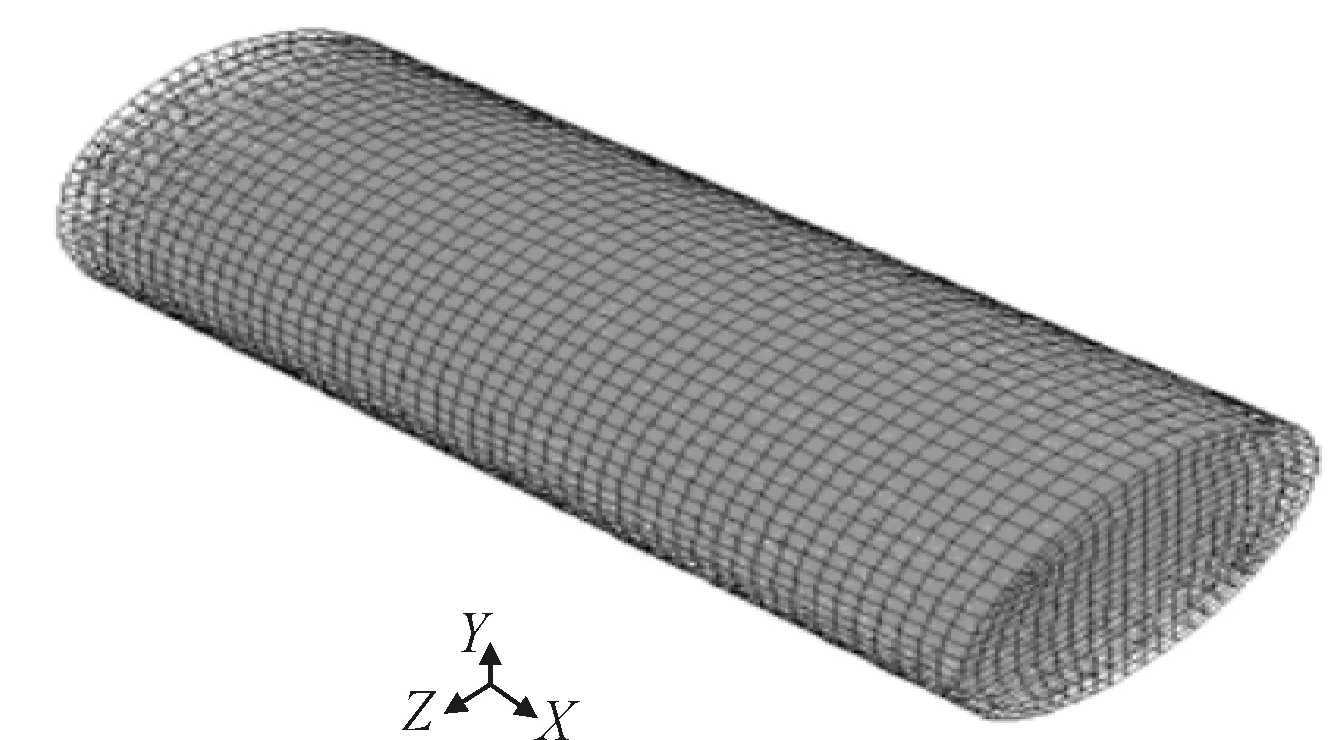
图3　等效平封头型卧式容器模型

根据图3建立的流体域模型，运用FLUENT进行非稳态计算，选用标准k-ε湍流模型，应用VOF模型，采用非耦合求解器。定义充装率K为液体体积与容器容积的比值。当充装率K=0.5时，液位h=1 000 mm，即h/R=1 000/1 000=1，假设容器和介质的共同初速度u0=2m/s。当t=0时刻，容器突然运动停止，内部介质开始以固有频率晃动。介质对前后封头的作用力Fx在0～50 s的变化见图4。

图4　介质对前后封头作用力的变化

分析其偏差原因，主要是由于在解析解的求解计算中采用的介质是理想无粘性的，而文中的数值模拟仿真过程考虑了流体粘性，粘性的作用导致流体晃动的一阶固有频率略小于解析解，这是符合规律的。这说明利用FLUENT软件，采用VOF方法，通过选用标准k-ε模型并设置合理计算步长，来分析储罐内部介质的晃荡问题是合理正确的。

表1　卧式容器介质晃动一阶固有频率计算表

2储罐VOF模型的建立

2.1模型条件

LNG储罐采用某15 m3LNG储罐，根据设计参数，首先利用SolidWorks创建几何模型，然后导入Hypermesh中划分流体网格，最后在Fluent中进行计算。坐标原点位于储罐的中心位置，x轴指向船舶运动方向，y轴垂直向上，z轴指向船舶运动的垂直方向。假设罐体为刚性，即不考虑流体载荷作用下罐体产生的运动及变形。整个模型采用四面体网格，网格总数54 077个，网格模型见图6。

图6　LNG储罐的网格模型

介质的类型不同、粘度不同对介质晃动现象影响很小[7]，很多学者在开展液体晃动的研究时普遍采用理想无粘性的介质。因此，釆用水和空气为流体介质，替代LNG，认为空气是理想气体。定义筒体及前后封头为壁面边界条件，罐内为气液混合流，水为液体部分，空气为气体部分，水和空气的比例为1∶1，即充装系数为0.5。

假设储罐在船舶上为纵向布置，即储罐轴线与船舶的运行方向一致。船舶以航速19.62 m/s沿x轴正向匀速行驶，t=0时刻，以2g的反向加速度进行制动，1 s后，船舶储罐停止运动，内部介质继续晃动。

2.2求解设置

本文采用VOF方法求解储罐内液体的晃动，求解器的设置如下：①瞬态模型；②压力基求解器；③绝对速度；④标准k-ε湍流模型；⑤速度压力耦合；⑥空间离散方案；⑦一阶隐式格式。

为了简化研究，同时取得较好计算结果，对VOF进行如下设置[8]。

1) 物性的定义。液体设定为水，气体设定为空气，液气比1∶1；水和空气的初始密度分别为998.2 kg/m3和1.225 kg/m3。

2) 流体相的定义。将空气设置为主相，水为第二相。

3) 重力加速度的定义。设置y向的加速度分量为-9.81 m/s2，即加速度方向沿y轴负方向。

4) 参考压力的定义。设置为100 kPa，参考点位置选为罐体最高点的中心处，即点(0,1,0)。

5) 工作流体密度定义。设定为1.225 kg/m3。

2.3制动速度的施加

很多文献中通过对流体施加制动加速度来模拟储罐的制动过程，这种惯性力的施加方式是不合理的，因为罐内液体晃动的根本原因是内部液体之间的相对运动。可见罐内液体在各点的加速度不同，且不等于制动加速度。由于储罐与船舶之间无相对运动，故储罐壁面与船舶具有相同的制动速度，可以对储罐壁面施加船舶制动的速度边界条件，以仿真储罐的内部液体晃动，从而反映船舶在制动过程中储罐内部液体晃动的真实情况。船舶制动的速度边界条件可通过编写UDF程序来实现[9]。

3储罐介质晃荡过程分析

3.1罐内的静压分布

FLUENT计算湍流运动时，要求网格必须具备较高质量。对已划分的网格进行测试，看其能否精确进行计算，暂不施加速度边界条件，在定义液位高度及相关参数后，求解罐内的静压分布并与理论值进行比较。储罐内的静压分布见图7。

图7　储罐内的静压分布

理论静压最大值pmax为

(1)

计算得Pmax=9.79 kPa

由图7可见，罐内静压由罐顶到罐底呈线性分布。罐底静压最大，最大值为9.78 kPa，与理论值非常接近，所以流体网格满足要求。

3.2冲击力的变化

液体在晃动过程中，储罐的前后封头均受到液体的冲击作用，这种作用常用冲击力表示。冲击力代表某表面所受的液体总作用力，可由压强沿表面积分求出。

制动开始后，内部液体受到惯性力作用而向前运动，当受到前封头的阻挡作用后，改向后封头运动。前后封头处的液体冲击力随时间的变化过程，如图8所示。从中可以看出：

1)t=0.090 s时，前封头所受的冲击力出现峰值，Fmax=1 342 276.5 N。

3) 前封头所受的冲击远大于后封头，前封头处所受的最大冲击约为后封头处的2.2倍。

4) 随着时间的不断延续，前后封头处的液体冲击力均趋向于零。

图8　前后封头所受的冲击力随时间的变化

由于液体冲击力对前封头的作用远大于后封头，因此下文中所述的冲击力均代表前封头所受的冲击力。

4充装率对晃荡过程的影响

本文研究储罐充装率对液体晃动产生的最大冲击力的影响，是在保持其他参数不变的情况下，通过改变储罐的充装率而进行的。储罐充装率K与液位高度h成正相关，可建立某种换算关系，因此，为分析方便，这里采用储罐的液位高度与罐体半径的比值(h/R)作为分析变量，分别取为0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9、1.0、1.1、1.2、1.3、1.4、1.5、1.6、1.7、1.8、1.85、1.9，共考虑19种工况。

充装率对储罐最大冲击力的影响见图9。制动过程中液体晃动对储罐产生的最大冲击力先随充装率的升高而增大；当h/R≥1.85，即充装率K≥0.97后，储罐所受的最大冲击力随充装率的升高而减小；充装率为0.97时，储罐所受的最大冲击力达到峰值。

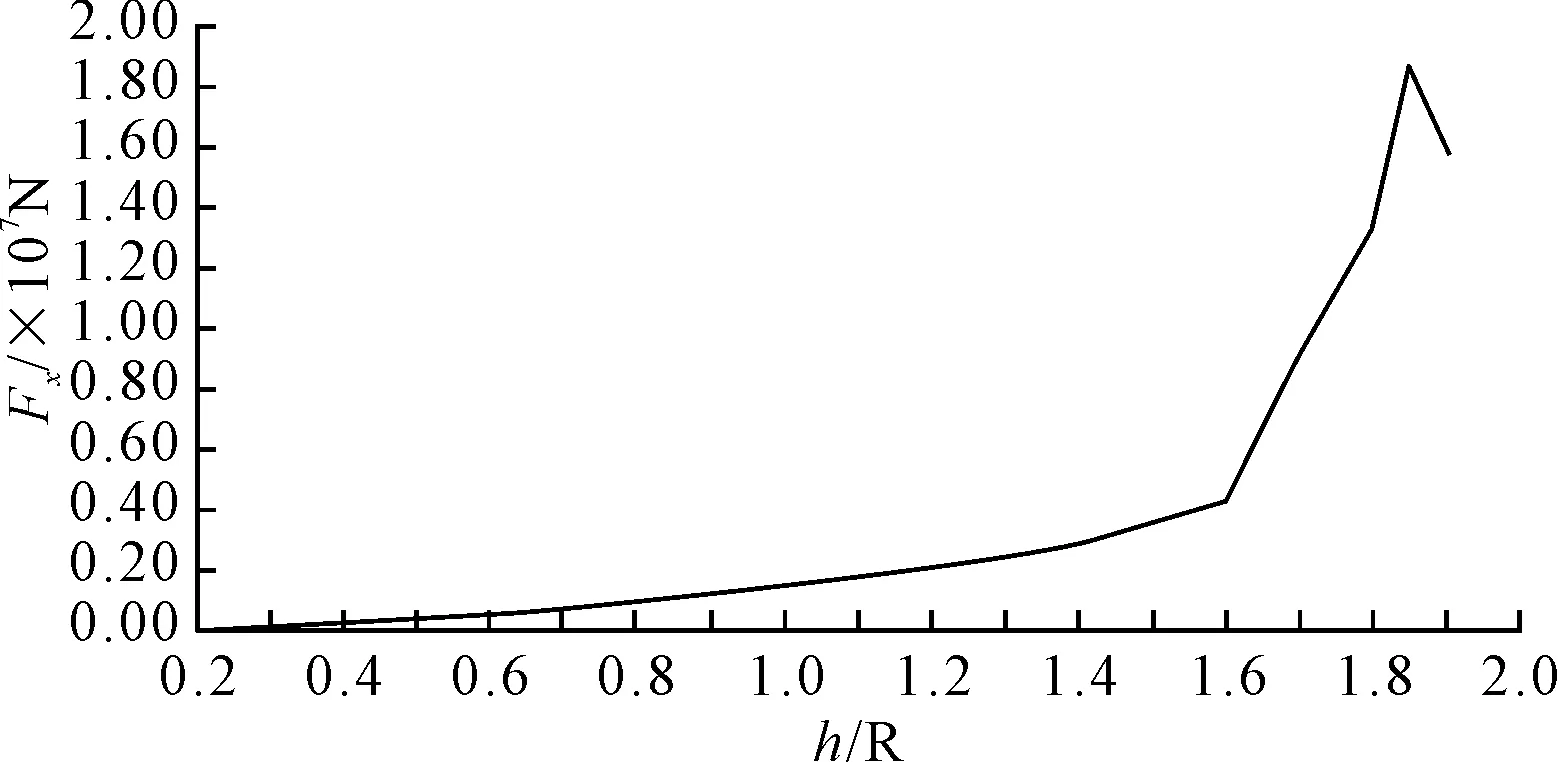
图9　不同充装率下储罐所受的最大冲击力

不同充装率下，储罐最大冲击力的出现时间，如图10所示。可见，随着充装率的升高，最大冲击力的出现时间不断提前，这正好表明液体涌向前封头的时间在不断缩短。

图10　不同充装率下最大冲击力的出现时间

5防波板对晃荡过程的影响

5.1设置一个防波板的罐体内介质晃动模拟

为了便于探究LNG储罐中防波板的防波效用，这里建立带防波板的储罐模型。罐体尺寸同前文一样，为了减小计算量，防波板采用无孔平板形式，如图11所示。出于优化网格质量的考虑，建立模型时将防波板的厚度由实际的3 mm增大至30 mm。由于防波板的厚度相对于储罐的轴向总长度很小，因此增加防波板的厚度对晃荡的影响不大。

图11　防波板结构示意

首先考虑只设置1个防波板的情况，即在储罐轴向的中间位置处安装1个防波板，整个流体域采用四面体网格，共63 194个。网格划分的情况，见图12。

图12　设置1个防波板的储罐网格模型

充液系统的初始速度v=19.62 m/s，充装系数K=0.50，制动加速度a=19.62 m/s2，1 s后储罐静止，内部介质进行自由晃动。储罐的前后封头(其中fengtou_left代表后封头，fengtou_right代表前封头)所受到的介质作用力，见图13。

图13　储罐的前后封头所受到的介质作用力(h/R=1)

图中虚线表示储罐中设置一个防波板的情况，实线代表没有设置防波板的情况。由图13可见，储罐内安装了一个防波板后：

1) 前封头所受的冲击力在开始制动的0.05 s内与不设防波板的情况基本相同，0.05 s后都小于不设防波板的情况。由此可见，设置防波板后，储罐在制动过程中前封头所受的冲击力得到了改善。

2) 后封头所受的冲击力在开始制动的0.03 s内与不设防波板的情况基本相同，0.03 s后后封头所受的冲击力开始急剧增大。这是由于此时后封头内部开始出现负压，后封头受到外压的作用，因此所受的冲击力急剧增大。

3) 前封头所受的冲击力在0.055 s时，达到最大值1 279 900 N，相比于不设防波板的情况，前封头受到的最大冲击力在幅值上有所下降，且出现的时间有所提前，这是由于防波板将储罐分割成了相对的2个空间所造成对的。

4) 前封头所受的冲击力多次达到极大值，而无防波板时冲击力仅在0.077 5 s和0.315 0 s 2次达到极大值，这是由于安装防波板后，防波空间变小，介质对封头的撞击频率增加造成的。

5) 对于储罐整体而言，安装1个防波板后，液体晃动的幅度减小，罐体受到介质在x方向上的总作用力相应减小，且在时间域的分布上相对平稳。

5.2防波板的数目对罐体内介质晃动的影响

当h/R=1时(见图14)，设置防波板后，船舶在制动过程中储罐所受液体的冲击力作用得到了改善。随着防波板数量的增加，储罐受到的冲击力曲线变化在时间域上的分布上更平缓；防波板数量超过1后，增加防波板数量对减小最大冲击力效果不显著，但是冲击力的极大值出现的更均匀，罐体受力更加平缓。

图14　不同防波板数量的储罐冲击力随时间变化(h/R=1)

当h/R=1.5时，如图15所示，随着防波板的数量增加，储罐受到的最大冲击力逐渐减小，冲击力曲线在时间域上的变化更平缓。

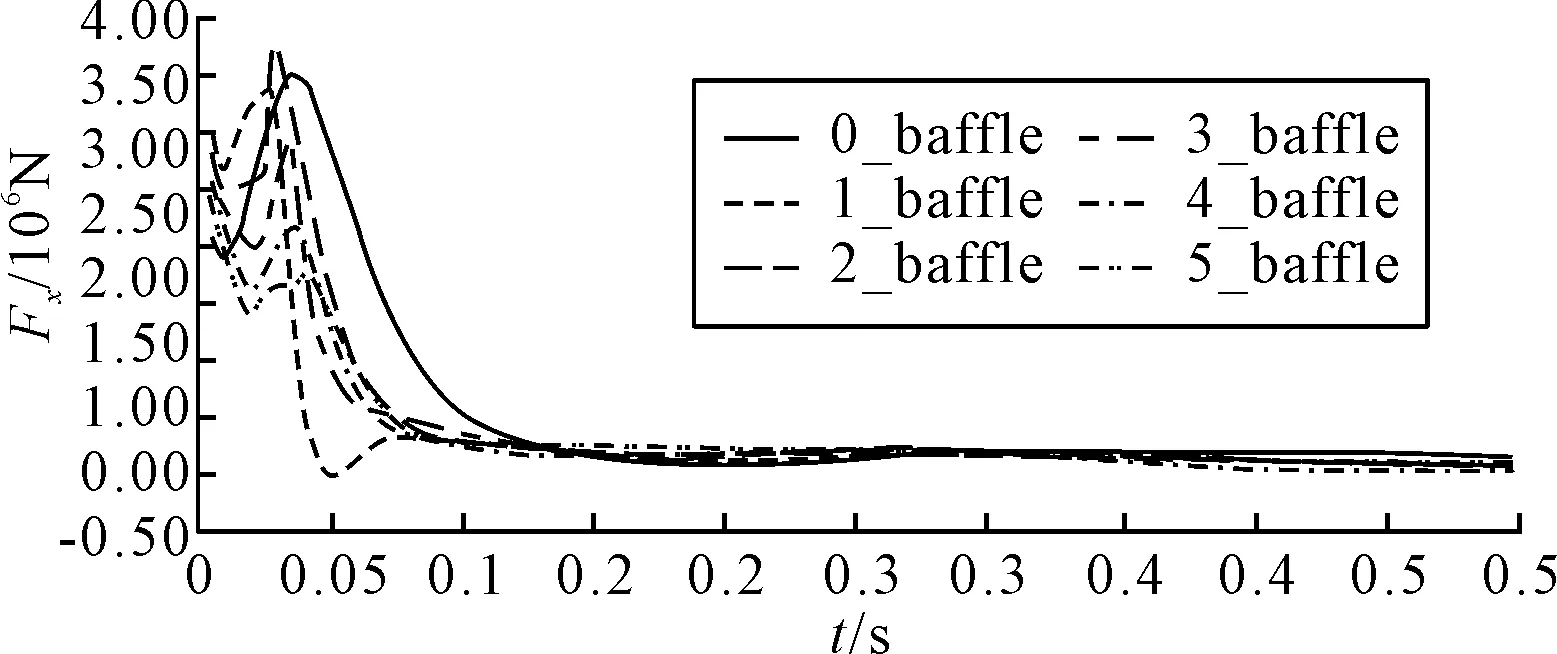
图15　不同防波板数量的储罐冲击力随时间变化(h/R=1.5)

从图15中可以看出，安装1块防波板时，储罐所受冲击力衰减最快；当防波板数量超过1后，增加防波板数量对加快冲击力的衰减效果不显著，但是冲击力的最大值会有所降低。

通过对不同液位时，不同数量防波板对储罐冲击力的影响分析，可以得出如下结论。

1) 随着防波板的数量增加，储罐所受的冲击力随时间的变化更平稳。

2) 储罐内的液位越高，防波板的作用效果越明显。

3) 随着储罐内液位的升高，储罐所受的冲击力出现峰值的时间提前。

4) 对于该15 m3的储罐，安装一块防波板就可达到较好的防波效果。

上述研究从理论上很好地验证了中国船级社在《天然气燃料动力船舶规范》中提出的“对于有效容积不大于25 m3的LNG气罐，每个防波段容积一般不大于7.5 m3”的建议的正确性[10]。

6结束语

利用ANSYS FLUENT软件，采用VOF方法，通过选用标准k-ε模型并设置合理计算步长，来分析储罐内部介质的晃荡问题是合理可行的。船舶制动过程中，前封头所受的冲击力远大于后封头，且随着晃动时间的延续，前后封头处的冲击力均趋近于零。随充装率的不断升高，液体晃动对储罐产生的最大冲击力先升高后下降，而最大冲击力出现的时间则不断提前。随着防波板的数量增加，储罐所受的冲击力随时间的变化更平稳，而储罐内的液位越高，防波板的作用效果越明显。对于15 m3的储罐，安装一块防波板就可达到较好的防波效果。文中防波板采用了简单的无孔平板结构，后续工作中可系统地开展各式防波板对液体晃动的影响研究。

参考文献

[1] 何晓聪,杨建国,周瑞平.船用LNG储罐的疲劳强度分析研究[J].船舶工程,2015(5):19-23.

[2] 刘东进,曹蛟龙,金全洲,等.基于CEL方法的船用LNG储罐防波板数值模拟分析[J].船海工程,2015(4):162-166.

[3] 岳宝增.三维液体大幅晃动数值模拟与液弹藕合动力学研究[D].北京：清华大学,1998.

[4] HIRT C W， NICHOLS B D. Volume of fluid (VOF) method for the dynamic of free boundary[J]. Compute.Phys,1981,39:201-225.

[5] 方杰.VOF法在水利水电工程中的应用和探索[D].南京：河海大学,2005.

[6] UTSUMI M. Low-gravity propellant slosh analysis using spherieal coordinates[J]. Journal of fluids and structures,1998(12):57-83.

[7] 陈志伟.移动式压力容器介质晃动数值模拟及防波装置研究[D].杭州：浙江大学,2006.

[8] 韩占忠.Fluent流体工程仿真计算实例与应用[M].北京：北京理工大学出版社,2005.

[9] 孙丽娜.基于流固耦合作用罐式集装箱的强度分析与研究[D].南昌：南昌大学,2012.

[10] 中国船级社.天然气燃料动力船舶规范[S].北京:人民交通出版社,2013.

Numerical Analysis of Liquid Sloshing in Marine LNG Tanks

HE Xiao-cong1, HE Rong2

(1 Zhoushan Office of China Classification Society, Zhoushan Zhejiang 316000, China;2 Zhejiang Seahead Ship Design and Research Institute Co. Ltd., Zhoushan Zhejiang 316000, China)

Abstract:If the filling rate of marine LNG tank was insufficient, the ship motion will induce the sloshing of liquid in LNG tank. The VOF method of sloshing analysis of tanks is proposed to conducting numerical simulation of liquid sloshing. The filling rate, the anti-wave plate and other factors affecting the sloshing process are analyzed. The results show that as the filling rate is increasing, the resultant impact force of sloshing increases firstly, then drops. Besides, one anti-wave plate can achieve good anti-sloshing effect for 15 m3 small tanks.

Key words:LNG tank; liquid sloshing; numerical analysis; anti-wave plate; filling rate

DOI:10.3963/j.issn.1671-7953.2016.03.003

收稿日期：2015-11-24

第一作者简介：何晓聪(1989—)，男，硕士，助理工程师 E-mail:xche@ccs.org.cn

中图分类号：U662.2

文献标志码：A

文章编号：1671-7953(2016)03-0012-06

修回日期：2015-12-13

研究方向:轮机工程；造船技术