计及机组频率调节特性的电力系统潮流模型研究

莫小锋

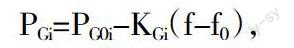
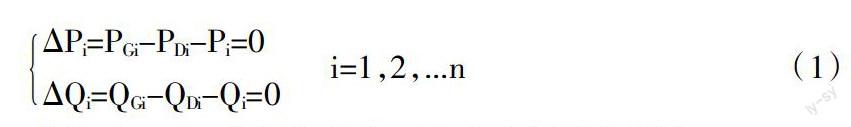
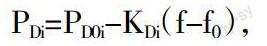
摘 要：文章在常规潮流模型的基础上，考虑了发电机组的一次调频作用，从而建立了计及机组频率调节特性的电力系统潮流模型。该模型满足在系统发生任一变动时，如切机、切负荷时，系统中所有机组均有参与一次调频的响应的实际情况。在此基础上，还建立了更加完善的计及系统频率调节特性的电力系统潮流模型。

关键词：一次调频；频率调节特性；静态特性；潮流模型

中图分类号：TM743 文献标识码：A 文章编号：1006-8937（2016）02-0077-02

1 电力系统潮流模型研究现状

严重的功率不平衡将导致的大规模系统频率波动事故，同时电网规模不断扩大与可再生能源发电集中并网已成为电力工业发展的必然趋势，其发电功率的间歇性与随机性导致其出力难以准确预测，随机波动幅度和频繁程度也都比传统的负荷功率波动大得多，这将必然导致系统频率发生不可预计的变动，也为电网的频率调整带来了新的挑战。

科技和经济的迅速发展导致电能的需求量日益增加，因此市场对电能质量的要求也越来越高。频率是衡量电能质量的三个基本标志之一，关系着发供电设备本身及广大用户电力设备的安全和效率，是交流电力系统和各类交流电气设备的重要参数之一。频率是反应电力系统电能供需平衡的唯一标志，而影响频率的主要因素是系统的有功功率：系统稳态运行中，有功发电功率和有功用电功率基本平衡，系统的频率基本稳定；若有功发电功率大于有功用电功率则会导致频率上升，反之将导致频率下降。因此，系统频率并不是一个恒定的值，而是随时变化的。电力系统的频率变动对电力系统和用户都会产生不利的影响，必须及时跟踪，密切关注，有效控制，因此需要用有效的手段及时进行频率调整。作为维持电力系统中有功功率供需平衡的主要措施，频率调整的根本目的是使电力系统频率保持稳定。发电机组原动机的自动调节转速系统是频率调整的主要手段，具有调频能力的发电机组的稳态运行点可用其有功功率静态频率特性表示，其出力可根据由系统中的扰动所导致的系统频率偏差来自动进行调节，即所谓的一次频率调节。当系统的功率平衡发生较大变动时，一次频率调节不足以调节系统的频率偏差，此时需通过系统中的调频机组进行二次频率调节来稳定系统频率。

电力系统潮流计算根据给定的网络拓扑结构、参数和运行方式确定整个系统的运行状态，是电力系统稳定计算和故障分析的基础，是实现电力系统安全经济发供电的必要手段和重要工作环节，是电力系统中应用最广泛、最基础和最重要的一种电气运算。因此潮流计算广泛的应用于电力系统的规划设计、生产运行、调度管理及科学研究。作为电网调度仿真的基础，潮流模型直接影响到仿真机的内在质量。由于电网调度仿真要求电网在各种不同运行方式下的潮流分布情况均能模拟，所以就要求潮流计算模型容易修改和调整，并具有很好的收敛性，计算结果也要符合电网的实际运行情况。

從数学的角度来说，潮流计算就是求解一组由潮流方程构成的非线性方程组，也就是求解潮流模型。在常规的潮流模型中，节点类型一般分为PQ节点、PV节点和平衡节点三类。由于在常规潮流模型只能得出系统频率为额定值时的潮流分布，并不能体现系统频率因不同扰动所产生的变化，因此需要在潮流计算中增加相应的方程以及对应项，并将频率作为求解量，从而判断系统频率是否能够满足电能质量要求，并以此作为根据实现系统的频率调整。

此外，由于常规潮流计算忽略了发电机组和负荷的静态特性，并将除平衡机以外的发电机有功出力设置为固定值，从而导致其计算结果与实际的运行情况有三点不符：①潮流发电机组的自动调节和机组所固有的静态特性导致并不存在具有无限大容量的理想平衡节点和具有无限大增益系数自动电压调节器的理想PV节点，PQ节点也与实际运行情况不符；②不同平衡节点的选择和平衡节点电压幅值的不同将导致不同的潮流计算的结果；③常规潮流计算中仅由一个平衡节点承担所有的功率不平衡量，不能准确地反映具有调频能力的发电机的出力随系统频率变动的调整情况，发电机和负荷的有功功率和无功功率不会随着系统频率和节点电压的变化而变化。

由此可见，常规潮流模型的上述弊端严重影响了潮流计算结果的准确性，同时也限制了其在扰动后潮流计算方面的应用。因此，常规潮流模型需要进行相应的改进从而获得符合实际运行情况的计算结果。

2 电力系统潮流模型

在常规潮流模型的基础上，建立三个新的模型：①计及机组频率调节特性的电力系统潮流模型；②计及系统频率调节特性的电力系统潮流模型；③计及系统静态特性的电力系统潮流模型。此外，将以计及系统静态特性的电力系统潮流模型为例，使用牛顿—拉夫逊法求解该模型。

2.1 常规潮流模型

给定电力系统的网络结构、参数和决定系统运行状况的边界条件，电力系统的稳态运行状态便随之确定。从数学上说，潮流计算就是要求解一组由潮流方程描述的非线性代数方程组。常规潮流模型作为电力系统潮流模型的基础，是电力系统分析中潮流模型研究的基础和出发点。在常规潮流模型中，系统的潮流方程为：

在完成潮流计算后，可根据相关公式求得平衡节点的注入功率和其余各机组的注入无功功率。常规潮流模型中，系统频率f恒定在额定值，因此系统中各发电机组的出力和各节点负荷均不受频率变动影响。

2.2 计及机组与计及系统频率调节特性的电力系统潮流 模型

在常规潮流模型的基础上，考虑机组的频率调节特性和负荷的频率调节特性，建立了计及机组频率调节特性的电力系统潮流模型、计及系统频率调节特性的电力系统潮流模型。

2.2.1 机组的频率调节特性

当负荷变动幅度很小，周期又很短时，将由发电机的调速器对负荷变动引起的频率偏移进行调整，即一次调频。当系统因功率缺额引起频率变化时，配置自动调速系统的发电机组的调速系统作用，调速器随机组转速的变动不断改变进汽量或进水量，使原动机的运行点不断从一根静态频率特性曲线向另一根静态频率特性曲线过渡。连接不同曲线上的运行点所形成的曲线即为发电机组的静态有功—频率特性曲线，为简化分析常以一条直线代替。当进汽或进水量已达最大值，调速器已不能再发挥作用，以致转速或频率进一步下降时，运行点只能沿对应最大进汽或进水量的频率特性转移，原动机的功率只能下降。

机组在某一稳态运行点时的静态调节方程可表示为：

其中，PG0i表示i节点上发电机组在系统发生变动前初始稳态运行状态下输出的有功功率，KGi为i节点上发电机组的有功—频率静态特性系数，f为系统频率，f0为系统发生变动前初始稳态运行状态时的系统频率。

2.2.2 负荷的频率调节特性

与发电机组的频率调节特性类似，当系统频率发生变动时，电力系统的负荷也会发生变动，其有功—频率特性曲线简化为直线。负荷在某一稳态运行点时的静态调节方程可表示为：

其中，PD0i表示i节点上负荷在系统发生变动前初始稳态运行状态下消耗的有功功率，KDi为i节点上负荷的有功—频率静态特性系数。

2.2.3 计及机组频率调节特性的电力系统潮流模型

在各参数给定的情况下，计及机组频率调节特性的电力系统潮流模型即为的非线性代数方程组。

在该模型中，一个有n个节点，g台发电机组（平均分布在g个节点上）的系统，有：①1个f、n-1个Ui、n-g个？啄i，（Us=1，？啄s=0取为电压幅值和电压相角的参考），共2n-g个待求变量；②同时可以列出n个有功方程，n-g个无功方程，共2n-g个方程式。显然，方程数等于待求变量数，所提潮流模型具有唯一解。完成潮流计算后，可计算各发电机组的有功出力情况以及各发电机组的无功出力情况。

2.2.4 计及系统频率调节特性的电力系统潮流模型

在各参数给定的情况下，计及系统频率调节特性的电力系统潮流模型即为非线性代数方程组。

在该模型中，一个有个n节点，g台发电机组（平均分布在g个节点上）的系统，有：①1个f、n-1个Ui、n-g个？啄i，（Us=1，？啄S=0取为电压幅值和电压相角的参考），共2n-g个待求变量；②同时可以列出n个有功方程，n-g个无功方程，共2n-g个方程式。显然，方程数等于待求变量数，所提潮流模型具有唯一解。完成潮流计算后，可计算各发电机组的有功出力情况以及各发电机组的无功出力情况。

3 结 语

根据电力系统的实际运行情况，在常规潮流模型的基础上，分别考虑了发电机组参与一次调频、系统负荷参与一次调频、发电机组无功出力与电压相关和负荷的综合静态特性，建立了计及机组频率调节特性的电力系统潮流模型、计及系统频率调节特性的电力系统潮流模型。所建模型在常规潮流模型的基础上，对潮流方程进行了一定的改进，使得潮流模型能够更加符合电力系统的实际运行情况，从而得出更加准确的潮流计算结果。使用牛顿—拉夫逊法求解高阶非线性代数方程组——潮流方程组能够得出潮流计算的结果，但其中的雅克比矩阵是待求变量的函数，因此在迭代过程中计算量较大。由于它是各种潮流计算方法的基础，因此在电力系统分析中有着特殊重要的地位。

参考文献：

[1] 陈衍.电力系统稳态分析[M].北京：中国电力出版社，2007.

[2] 杭乃善，周航，李如琦.稳态控制潮流的设定空载频率及空载电压算法 [J].中国电机工程学报，2003，（12）.

[3] 包黎昕，宋志东.考虑发电机约束条件的潮流计算方法[J].中国电机工 程学报，1998，（9）.

[4] 于继来，王江，柳焯.電力系统潮流算法的几点改进[J].中国电机工程学 报，2001，（9）.

[5] 毛艳丽.考虑频率特性的互联电网潮流与最优潮流模型研究[D].重庆：重庆大学，2014.

[6] 段瑶.计及电力系统静态特性的快速潮流计算及其相关应用研究[D].武汉：华中科技大学，2013.