基于Buckingham模型和Biot-Stoll模型的南沙海域沉积物声速分布特征

王景强, 郭常升, 刘保华, 陈文景, 侯正瑜, 韩国忠

1)国家海洋局第一海洋研究所, 海洋沉积与环境地质国家海洋局重点实验室, 山东青岛 266061; 2)中国科学院海洋研究所, 中国科学院海洋地质与环境重点实验室, 山东青岛 266071; 3)国家深海基地管理中心, 山东青岛 266061; 4)青岛海洋科学与技术国家实验室, 海洋地质过程与环境功能实验室, 山东青岛 266061; 5)中国科学院大学, 北京 100049



基于Buckingham模型和Biot-Stoll模型的南沙海域沉积物声速分布特征

王景强1, 4), 郭常升2, 4)*, 刘保华3, 4), 陈文景2, 5), 侯正瑜2, 5), 韩国忠1, 4)

1)国家海洋局第一海洋研究所, 海洋沉积与环境地质国家海洋局重点实验室, 山东青岛 266061; 2)中国科学院海洋研究所, 中国科学院海洋地质与环境重点实验室, 山东青岛 266071; 3)国家深海基地管理中心, 山东青岛 266061; 4)青岛海洋科学与技术国家实验室, 海洋地质过程与环境功能实验室, 山东青岛 266061; 5)中国科学院大学, 北京 100049

摘 要:为了选择合理的南海南部海底沉积物的声速反演模型, 分别利用Wood方程、Buckingham模型、Biot-Stoll模型等声波传播理论模型计算了沉积物的纵波声速, 结合沉积物实测声速和物理参数等, 对比了模型计算声速与实测声速的变化特征。声速实测值与模型计算值的对比表明, Buckingham模型计算值与实测值的平均偏差最小。研究区实测声速比和模型计算声速比的分布表明, 声速的变化特征与沉积环境具有相关性, 声速模型计算值与实测值具有相似的变化特征; 模型计算声速与实测声速的垂向变化规律不相同,模型计算声速随深度基本不变, 而实测声速在陆架、陆坡和海槽等沉积环境中呈现出多种垂向分布特征。研究结果认为, 侧重于沉积物孔隙性的Biot-Stoll理论仅适用于陆架区粗颗粒沉积物, 兼具流体和弹性固体双重性质的Buckingham理论具有更广的适用范围。该研究对获取南海南部海域沉积物声速分布特征有重要意义, 可为多波束测深或浅地层精细解释等提供基础资料。

关键词:海底沉积物; Buckingham模型; Biot-Stoll模型; 声速分布特征; 声速比

本文由海洋公益性行业科研专项经费(编号: 201405032; 200905025)和国家自然科学基金重点项目(编号: 41330965)联合资助。

海底松散沉积物通常被作为一种液固两相介质, 主要由砂、粉砂、黏土和孔隙流体(海水)等物质组成。海底表层沉积物构成了海水的下边界和沉积物的上边界, 从海底表层到深层, 沉积物由未固结松散介质变为半固结, 乃至固结沉积物介质(邹大鹏等, 2012a)。相对于结构密实的深层沉积物, 作为海水与深层沉积物分界面的表层松散沉积物(1 m埋深范围内的沉积层), 具有更复杂的声学特性和独特的声学指示意义, 其声速的分布特征是海域声场环境的重要部分, 也是进行海洋多波束或浅地层精细解释的基础资料。目前获取海底沉积物声学参数的方法, 主要包括理论模型预测、经验方程预报和声学参数测量等。许多研究学者利用取样测量方法(Hamilton, 1985; Lu et al., 2010)和原位测量技术(Briggs and Richardson, 1997; Liu et al., 2013; Hou et al., 2014)进行了大量的海底沉积物声学测量工作,建立了声速与物理参数之间的经验公式, 探讨了声学性质与物理性质之间的关系, 这些声学实测工作为验证声波传播理论模型的有效性提供了基础资料。目前建立的声波传播理论模型主要包括Biot-Stoll模型(Biot, 1956a, b; Stoll, 1989; Stoll and Bautista, 1998; Chotiros and Isakson, 2004; 朱祖扬等, 2013)、Wood方程(Jackson and Richardson, 2007) 和Buckingham模型(Buckingham, 1997, 1998)等。声波传播理论模型的有效性得到了声学实测的分析和验证, Williams等(2002)基于SAX99声学试验, 比较了理论模型预测值与海底沉积物声学实测值, 结果表明Biot理论和等效流体近似理论能够匹配声速的频散特征, 但不能准确表述衰减随频率的变化趋势,而衰减和频率的关系与Buckingham理论预测结果能够实现最佳拟合。Buckingham(2005)系统地比较了声波速度和衰减的模型预测值与实测值, 认为高频段时衰减与频率之间具有近似的线性关系, 而低频段的声衰减与频率呈近似平方关系。这些声学测量和模型预测的对比基于实验室沉积物模型, 对声速和声衰减频散特征进行比较, 缺乏与沉积物所处海域的沉积环境相联系。因此, 需要分析声波传播模型在复杂沉积环境声学参数预测中的适用性, 从而为海底沉积物选择更有效的声学反演模型, 有利于实现快速反演复杂环境沉积物的声学特性。

南海南部海域覆盖大陆架、大陆坡及南海海槽等多种地貌单元, 其沉积物具有复杂的分层结构,从而影响了物理性质和声学特性的分布特征。因此,需要结合实际声学测量分析复杂沉积环境对纵波声速分布特征的影响, 从而选择合理的声速计算预测模型。张福生等(2001)根据沉积物声速与底层海水声速的比值(声速比R)将该海域的表层沉积物分为高声速和低声速两类, 但没有分析声速的空间分布特征。针对该研究区Biot-Stoll模型参数的选择, 陈静等(2012)分析了Stoll参数和Schock参数的模拟匹配效果, 但缺乏与其他理论模型的对比。本文将基于研究区沉积物的声学测量资料, 分别利用Wood方程、Biot-Stoll模型和Buckingham模型等声波传播理论模型进行纵波声速计算, 并与实际测量获取的沉积物声速值进行对比, 分析不同地貌单元中模型预测声速的有效性。根据模型计算声速比和实测声速比的分布特征的对比, 探讨理论模型对复杂沉积环境声速分布特征的适用性。

1 海底沉积物声波传播理论

海底沉积物声波传播理论主要包括流体理论、弹性理论及多孔弹性理论三种类型, 分别把海底沉积物看成流体、弹性固体和多孔弹性介质。上述三种类型的声波传播理论均可归入“等效介质”理论的范畴。由于声波波长远大于沉积物颗粒的尺寸,可以把海底沉积物看作连续介质, 该连续介质的物理性质参数可以通过求取一定范围内的不同的微观测量值的平均值而获得。如果声波频率很高, 声波波长与颗粒的尺寸及孔隙的尺寸差不多时, 此时等效介质理论不能正确地描述沉积物中的波动现象。

1.1流体理论

流体理论假定海底沉积物中声波引起的应力可以用压力场和相应的波动方程来描述, 其所需要的主要参数包括声速、声衰减及沉积物和海水的密度等。该理论将海底沉积物看成连续介质, 把一定体积内包含许多沉积物颗粒的物理参数平均值作为沉积物物理参数的数值, 对一定体积的沉积物单元体的等效密度和等效体积模量建立方程, 并得到沉积物声速的计算公式, 即Wood方程(Jackson and Richardson, 2007)。该方程忽略了沉积物颗粒间相互接触产生的力, 也没有考虑孔隙流体与介质骨架间的相对运动, 即忽略了惯性力和黏滞力, 因此其具有很大的声速预测误差和应用的局限性, 其对不太注重沉积物颗粒接触力和密度差异影响的实验室模型测量可以做出合理的解释。沉积物单元体的等效密度ρ0和体积模量Kb的表达式分别为:

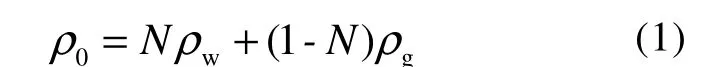
式中, N为孔隙度, ρw为水密度, ρg为沉积物颗粒密度; Kw为水的体积模量, Kg为沉积物颗粒的体积模量。根据式(1)、(2)和(3)可得出沉积物声速c0计算公式:

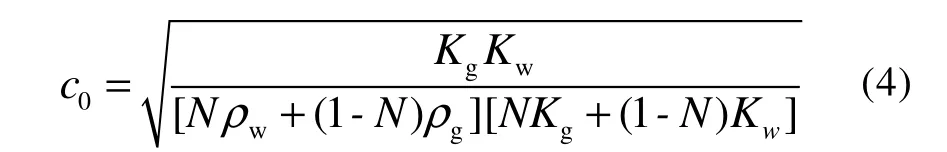
1.2弹性理论

声波传播弹性理论考虑了固体颗粒的弹性性质和流体理论所未考虑的剪切力的效应。对于黏土、粉砂和砂质沉积物, 剪切波传播速度非常低, 远低于海水的声速。Gassmann方程(Berryman, 1999)基于弹性理论, 考虑了流体饱和多孔介质的固体颗粒骨架的弹性性质, 但忽略了孔隙介质的孔隙流体和介质骨架间的相对运动, 不适于讨论渗透系数较大的沉积物的声波传播特性。基于弹性理论和流体理论, Buckingham模型假定沉积物颗粒相互接触但没有胶结, 颗粒间存在一种类似于黏滞作用的力, 因此该理论兼具流体和弹性固体的双重性质(Buckingham, 1997, 1998)。该模型以颗粒粒径为主要参数, 建立了单一频率下近似流体沉积物的声速cp预测方程:

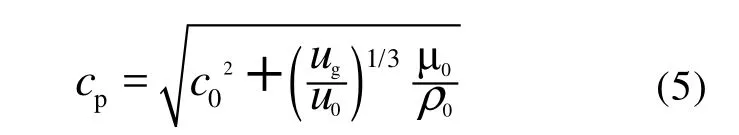
式中, µ0为纵波摩擦刚性常数, 取值为2×109Pa; ug为沉积物颗粒粒径; u0为参照粒径, 取值为1 000 µm; ρ0和c0与Wood方程相同。

1.3多孔弹性理论

Biot理论是一种经典的多孔弹性理论(Biot, 1956a, b), 同时考虑介质的孔隙性与弹性, 用来描述弹性波在固体和流体应力相互作用下的传播特征。Stoll(1989)将Biot理论应用于海底沉积物介质中的声速和声衰减计算, 建立了Biot-Stoll理论。该理论认为固体颗粒构成了与孔隙流体相耦合的弹性骨架, 流体中的声波与骨架中的纵波和剪切波混合在一起, 构成了三种波: 快纵波、慢纵波和剪切波。该理论结合沉积物颗粒间胶结差、骨架模量低的特点, 认为骨架耗散是声波能量衰减的重要原因, 骨架耗散的大小与频率无关, 而流体黏滞耗散则随频率的变化而变化。理论本构方程涉及的13个参数通过测试或者曲线拟合的方法进行确定。Biot理论弹性模量、附加弹性模量、和复弹性模量可利用孔隙度N, 骨架体积模量, 骨架剪切模量孔隙流体体积模量Kw和颗粒体积模量Kg表示为:

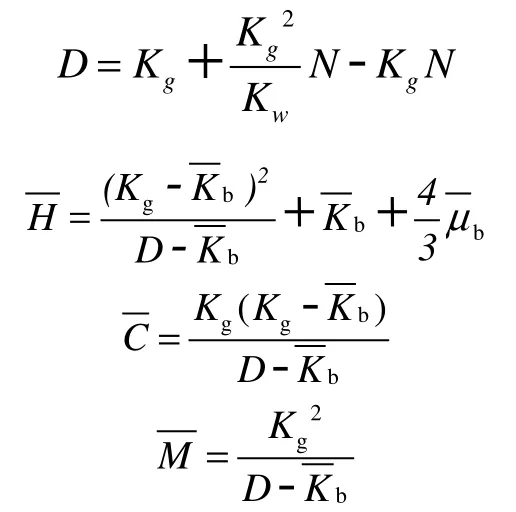
式中, Kw, Kg为实数。和为复数, = K0（1 + iδk） , = μ0（1 + i δμ） , δk为体积耗散系数, δµ为剪切耗散系数。

根据Biot-Stoll模型理论, 频率域的纵波传播方程可以写成公式:

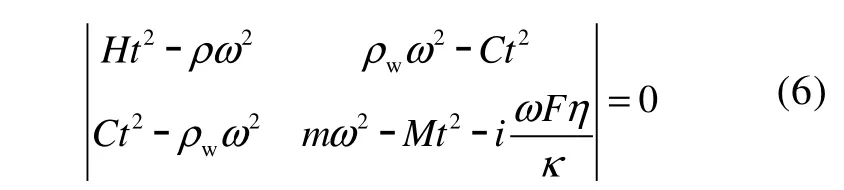
式中, ρ为沉积物介质密度, ρw为孔隙流体密度；t为复波数, ƞ为黏滞系数, κ为渗透系数, ω为角频率, m为有效密度, m=αρw/N, α为孔隙弯曲因子, F为高频校正因子。其中, 复波数k=ω/ cb+ i α , 可以得到声速cb的计算公式:

其中, Re(x)为复数x的实部。

2 试验测量与理论计算

2.1区域概况及数据获取

研究区域位于南海南部海域, 覆盖了大陆架、南沙台阶和南沙海槽等多种海底地貌单元, 水深100～3 000 m(图1)。陆架区沉积物一部分来源于现代浅海相沉积, 一部分属于早期残留沉积, 其沉积物组成既受到物源区沉积物自身特征的影响, 还受到后期改造作用的影响, 含量较多的粗颗粒物质主要是高能环境中长期沉积的产物, 在冰后期海平面上升的过程中, 可能被细颗粒沉积物覆盖(杨涛等, 2003), 呈现出粗颗粒与细颗粒沉积物相互交错沉积的特征。水深大于1 000 m的陆坡主要为深水区,地形和物源等环境因素更为复杂, 沉积物主要是细颗粒的黏土质粉砂和粉砂质黏土, 物源以生物源碎屑和陆源风成黏土等为主(李傲仙等, 2005; Liu et al., 2013), 由于陆坡水深变化较大且沉积速率较快(付淑清等, 2008), 沉积搬运作用强烈, 加上东北岛礁区覆盖粗颗粒珊瑚砂, 使得整个陆坡沉积物物理性质分布的局部变化特征更为突出(李赶先和龙建军, 2014)。南沙海槽的槽谷较为平坦, 水动力条件较弱, 沉积物埋藏后期剥蚀和搬运作用较弱, 主要受压实作用影响, 覆盖有较厚的沉积物, 细颗粒物质含量高, 以粉砂质黏土和黏土质粉砂为主。

图1显示了研究海域的位置, 站位深度136～2 843 m。沉积物柱状样品由科考船“科学一号”于2012年5月采用重力柱状取样器进行采集, 每根样品长100 cm。样品取回甲板后, 以15 cm为间距,采用WSD-3数字声波仪和同轴差距法进行了声学测量, 测量频率为100 kHz。其中样品长度测量精度为0.05 cm, 声时测量精度为±0.1 µs。声学测量完成后封存沉积物样品, 后期在实验室进行样品的湿密度、孔隙度和粒度分析测量测试。其中, 沉积物的颗粒组成和粒径利用Cilas 940L型激光粒度仪进行测试。图2为声学测量和物理参数测量的沉积物层位图。通过声学参数测量和物理参数测量, 获得15 cm、30 cm、60 cm、75 cm、90 cm等6个埋深层位共计126组样品的声速和孔隙度、湿密度、粒径、颗粒组分含量、颗粒密度等物理参数。

图1　研究区域示意图Fig. 1 The study area

由于甲板实验室声学测量时, 沉积物的温度和压力等环境参数会发生改变, 需要获取沉积物原位的温度压力参数(Hamilton, 1971; 邹大鹏等, 2012a),校正计算得到沉积物的原位声速和近底上覆海水的声速。根据CTD实测资料确定21个站位的底层海水温度在1 . 5 ～ 1 6℃, 沉积物的测量温度在12～18℃。通过海水声速剖面、底层海水的温度、深度和盐度等参数, 分别利用Hamilton校正法(Hamilton, 1971)和Wilson海水声速公式(周丰年等, 2001), 精确计算校正了沉积物的声速和近底上覆海水的声速, 并根据校正的沉积物声速和近底上覆海水声速计算得到沉积物的声速比, 其中声速的范围为1 402～1 627 m/s, 声速比的范围为0.94～1.07,该结果与张福生等(2001)在该海域测量结果的变化范围相一致。

2.2海底沉积物的物理参数

由于理论模型均涉及较多的参数, 参数的选取对计算结果有不同程度的影响, 所以针对研究区域选取合理的参数是必要的。Wood方程和Buckingham模型的主要参数为孔隙水密度、颗粒密度、孔隙度、粒径、颗粒体积模量、孔隙水体积模量等。除上述参数外, Biot-Stoll模型还需要输入更多的参数, 包括渗透率、流体黏滞系数、骨架体积模量、骨架剪切模量、孔隙因子、高频校正因子等。通过物理性质测试获取了颗粒密度、孔隙度、湿密度、粒径等参数, 其余参数均需要利用经验公式计算或从文献资料中获取。表1为本文详细的参数取值, 其中渗透率、沉积物孔隙因子、颗粒体积模量和剪切模量、孔隙水体积模量等参数根据Stoll和Bautista(1998)、Buckingham(1998, 2005)模型和Jackson和Richardson(2007)的专著“High-Frequency Seafloor Acoustics”(高频海底声学)等文献资料的参数变化范围进行搜索优化拟合确定或基于Schock(2004)公式利用实测物理参数计算得到。

3 结果与讨论

3.1声速实测值与声速预测计算值比较

图2　沉积物柱状样声学测量层位Fig. 2 The acoustic measured horizons of sediment samples

表1　海底沉积物的物理参数Table 1 Physical parameters of marine sediments

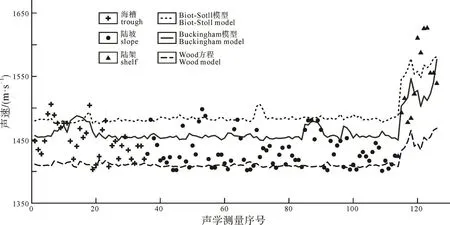
图3　声速实测值与声速预测计算值比较Fig. 3 The comparison between the measured and the calculated sound speeds

为比较声速预测值与实测值, 分析声速预测模型的适用性, 分别采用Wood方程、Buckingham模型和Biot-Stoll模型声速预测方程进行了声速计算,计算所采用的参数见表1。图3显示了声速实测值与计算值的比较结果: 三种模型计算声速的变化曲线与实测声速具有大体相同的变化趋势, 陆架区沉积物的声速明显高于海槽和陆坡沉积物的声速。

经过差值计算, 实测值与Wood方程计算值的平均偏差为3.17%, 实测值与Biot-Stoll模型计算值的平均偏差为2.15%, 实测值与Buckingham模型计算值的平均偏差为0.87%。从图3中可以看出, 相对于声速实测值, Wood方程计算的声速值偏小, Biot-Stoll模型计算的声速值偏大。在陆坡和海槽区, Biot-Stoll模型计算值为实测值值域的上限, Wood方程计算值为实测值值域的下限, Buckingham模型计算值介于二者之间。在陆架区, Wood方程计算值低于实测值的值域范围, Biot-Stoll和Buckingham模型的预测值与实测值更为接近。相对于低声速段, Biot-Stoll模型在高声速段的反演效果较好, 这与陈静等(2012)在该海域的计算结果相一致。

相对于另外两种模型, Wood方程对沉积物声速的预测误差较大, 这与过往研究的结果相一致(Hamilton and Bachman, 1982), 主要原因在于该模型忽略了海底沉积物中颗粒间相互接触的力, 还未考虑孔隙流体和颗粒骨架相对运动的黏滞力, 而这两种力是沉积物的高频声学测量需要着重考虑的内容。海底沉积物作为一种弹性介质, 具有一定的刚性, 并不是纯粹的流体, 其刚性与沉积物颗粒间的接触作用有关, 因而Wood方程适合于解释不注重颗粒接触力和密度差异影响的沉积物的声学特性(Jackson and Richardson, 2007)。不同于Wood方程, Buckingham模型和Biot-Stoll模型既考虑了固体颗粒骨架的弹性性质, 还考虑了孔隙流体和骨架相对运动的黏滞力对声波传播产生的影响, 因而这两种模型更适用于表达沉积物的声波传播特征。陆架区的砂质沉积物作为多孔弹性介质, 陆坡和海槽的松软泥质沉积物作为流体饱和多孔介质, 单一模型还不能完全解释和准确表达声波在多类型沉积物中的传播特征, 基于介质的多孔弹性效应且侧重孔隙性的Biot-Stoll理论仅适用于陆架区沉积物, 而兼具流体和弹性固体双重性质的Buckingham理论, 具有相对较广的适用范围。

3.2沉积物声速变化特征

沉积物声速的空间变化特征包括横向和垂向两部分, 是海底声场结构、海域地声模型的重要组成部分。声速的横向变化特征指示声速与沉积物物理性质和沉积环境的关系, 而声速垂向的变化规律是建立声速结构模型的重要依据。图4、图5和图6分别显示了实测声速比、Buckingham模型计算声速比和Biot-Stoll模型计算声速比的变化规律, 可以分析出研究区沉积物声速的横向和垂向变化特征, 识别研究海域的高声速区和低声速区; 还可以通过对比实测声速与计算声速的变化规律, 探讨利用Buckingham模型和Biot-Stoll模型预测分析复杂环境沉积物声速变化特征的适用性。

3.2.1沉积物声速平面的变化规律

根据该海域沉积物实测声速比变化特征图(图4)可以看出, 西南陆架区在15～45 cm深度范围的声速比小于1, 属于低声速区; 在60～90 cm深度范围的声速比大于1, 属于高声速区。陆坡和海槽区的大部分声速比低于1, 局部区域甚至低于0.95, 均属于低声速区。由此可知, 研究海域的高声速沉积物主要分布于西南陆架和东北岛礁区, 而低声速沉积物广泛分布于陆坡和南沙海槽。

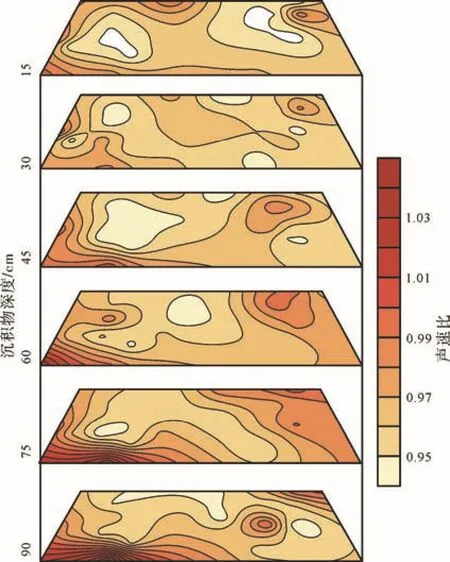
图4　沉积物的实测声速比的变化特征Fig. 4 The distribution of the measured sound speed ratios

物理参数测量结果显示, 陆坡和海槽沉积物类型以粉砂质黏土和黏土质粉砂为主, 其中粉砂含量为40%～60%, 粒径范围为3～5 μm, 湿密度范围为1.1～1.4 g/cm3; 西南陆架的沉积物类型则以砂质粉砂为主, 砂含量为20%～50%, 粒径范围为30～70 μm, 湿密度范围为1.46～1.83 g/cm3。根据大陆架、陆坡和海槽沉积物实测物理参数, 主要的物理性质呈现有规律的变化: 大陆架沉积物表现为粗颗粒、低孔隙度、高密度; 陆坡和海槽沉积物则呈现细颗粒、高孔隙度、低密度。这表明声速比的分布特征与物理性质、沉积环境等因素具有相关性。究其原因, 沉积环境决定了沉积物的孔隙度、粒径、密度等物理性质, 而物理性质又是影响沉积物声速的重要因素, 因此声速的分布特征宏观上受到沉积环境的控制。

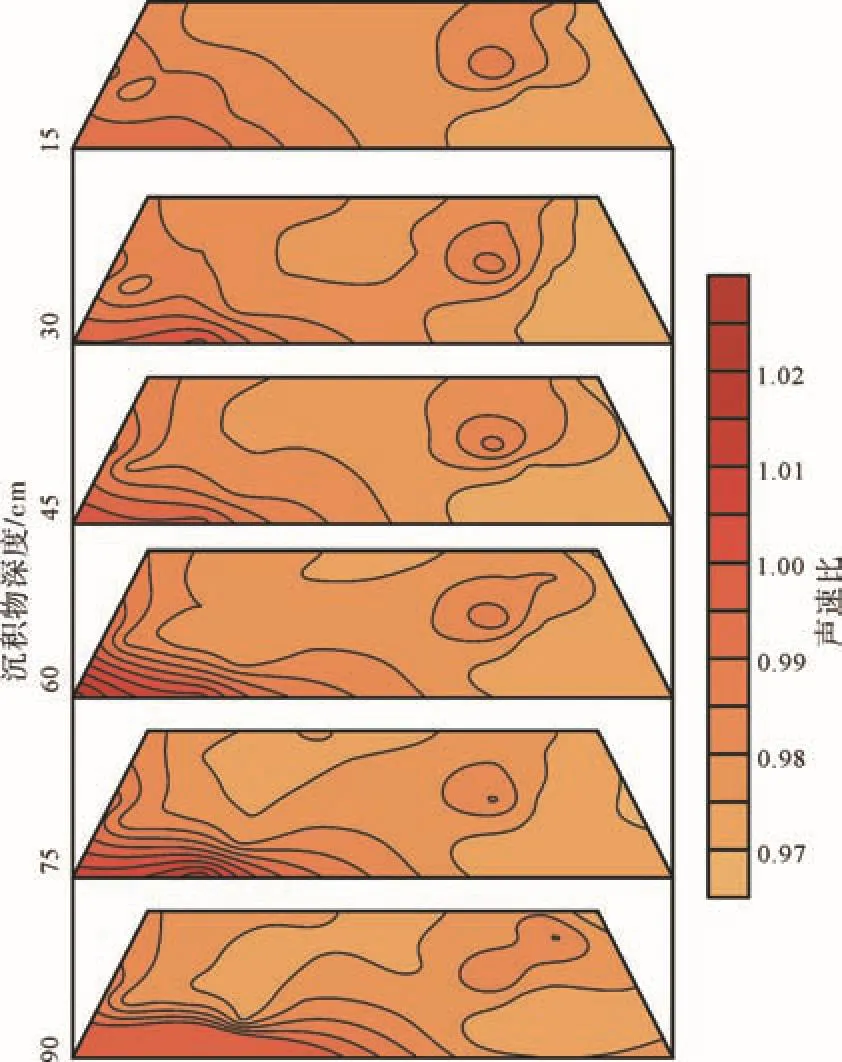
图5　Buckingham模型计算声速比变化特征Fig. 5 The distribution of the calculated sound speed ratios based on Buckingham model

图6　Biot-Stoll模型计算声速比分布Fig. 6 The distribution of the calculated sound speed ratios based on Biot-Stoll model

3.2.2沉积物声速垂向的变化规律

通常认为, 由于上覆沉积物载荷压力的增加和固结作用导致沉积物结构发生变化, 其密度、粒径等具有增大的变化特征, 而孔隙度、含水量呈现减少的趋势, 从而使得沉积物声速呈现随深度增大的变化特征。然而这种认识与实际声学测量的研究结果不一致: Hamilton(1980)建立了浅海大陆架和深海丘陵、深海平原的地声模型, Lu等(2003)提出了南海北部大陆架低声速和高声速海底的声速结构模式, 这些研究均认为沉积物声速及物理性质呈现多种垂向的变化模式。然而这些地声模型基于多个海域数米乃至数十米埋深的沉积物, 采用的测量手段也不相同, 具有较大的声学测量尺度, 是否能阐述表层松散沉积物的声速分布特征有待验证。

从研究区实测声速比分布图(图4)可以看到,研究区沉积物声速整体上随深度呈现增大的趋势,但在不同的沉积区域呈现出多种变化规律。西南部陆架区和东北岛礁区沉积物的声速在15～90 cm深度呈现逐渐增大的变化趋势, 这是由于陆架区主要为陆源碎屑沉积物, 粗颗粒成分在该区沉降下来,而细颗粒成分被搬运至深水区, 先沉降沉积物受到后期沉积物载荷压力的作用, 结构密实且孔隙度相对较小, 而表层沉积物的结构较为松散且具有较大的孔隙度。东北区岛礁周围覆盖粗颗粒的浅海珊瑚砂, 与钙质成分的深海泥质沉积物相比, 岛礁区沉积物的孔隙度和抗压强度相对较低(李赶先和龙建军, 2014), 表层沉积物固结时间较短其结构较为松散, 而随着埋深增加, 沉积物结构逐渐被压实。由孔隙度和声速的相关关系可知, 这两个区域沉积物的声速呈现出增大的垂向分布规律。陆坡和海槽沉积物的声速随深度的变化特征较为复杂: 部分区域的沉积物声速呈基本不变的趋势, 这是由于水深变化相对较小且沉积物来源单一, 后期改造作用较弱,沉积物的物理性质随深度的变化幅度较小; 而部分区域沉积物的声速随深度呈现增大的趋势, 主要原因与陆架区相似, 受上覆沉积物载荷压力的增加的影响。上述变化趋势表明, 研究海区海底的声速结构模式既包括垂向增大模式, 还包括垂向不变和垂向复杂变化等多种模式, 这与过往的研究结果相一致(Lu et al., 2003; 邹大鹏等, 2012b; Wang et al., 2014)。究其原因, 沉积物的声速与物理性质具有相关性, 而物理性质受沉积环境和沉积结构的分层性所影响, 物理性质尤其是孔隙度易受压实作用的影响, 随深度呈现出多种变化趋势, 从而决定了声速随深度变化的复杂特征。因此, 较之深层沉积物受到压实和固结作用的影响从而具有较为密实的结构,表层沉积物的结构相对较为松散, 其声学性质介于流体(海水等)和固体(密实的沉积物、岩石等)之间,不能利用单一声波传播理论描述声波在表层沉积物中传播的特征, 也不能用单一的声速垂向增大模式描述所有海域沉积物的声速结构。

3.2.3Buckingham模型计算声速与实测声速的变化特征对比

根据Buckingham模型计算声速比变化特征图(图5), 西南陆架区沉积物声速比大于1, 属于高声速区。陆坡和南沙海槽沉积物的声速比普遍小于1,属于低声速区。与实测声速比的分布特征相类似,计算声速的平面分布特征与物理性质、沉积环境具有相关性, 但较之实测声速分布特征的复杂性和局部性, 计算声速比的平面变化特征较为单一且缺乏突变的特点。从声速比垂向的分布角度来看, 陆架区沉积物的声速比垂向上呈现小幅度增大的趋势,陆坡和海槽区沉积物的声速比垂向上基本不变, 这与实测声速比的垂向分布特征不一致。这表明, 利用Buckingham模型计算的声速比可以匹配实测声速比的横向分布特征, 但不能体现实测声速比分布的复杂性及变化幅度大等特点, 也不具备实测声速比垂向分布规律的多样性。

3.2.4Biot-Stoll模型计算声速与实测声速的变化特征对比

根据Biot-Stoll模型计算声速比变化特征图(图6)分析, 与实测声速比和Buckingham模型计算声速比分布相似, 陆架区沉积物具有较高的声速比, 陆坡和海槽沉积物的声速比相对较低。大部分区域沉积物的声速比大于1, 属于高声速区, 仅陆坡和海槽局部区域的沉积物声速比小于1, 属于低声速区。这表明Biot-Stoll模型计算声速符合陆架区声速的变化特征, 但不能匹配陆坡和海槽区声速比的平面变化规律。计算声速比垂向上呈现基本不变的特征,这与实测声速比垂向的变化规律不一致。由上述分析可知, 与Buckingham模型相类似, Biot-Stoll模型计算声速比能匹配实测声速比的平面分布特征, 但不能体现实测声速比垂向变化的复杂性及局部突变等特征。

综合图4至图6进行分析, 虽然两种模型计算声速的分布均与实测声速的分布特征具有相似性,但实测声速的分布具有复杂性和局部性。这表明理论模型预测不能完全体现复杂沉积环境对声速分布的影响。究其原因, 由于砂质和泥质等类型沉积物的物理性质之间存在着较大的差异, 不同类型沉积物的声速分布特征也不一致。即使沉积物的类型相同, 但沉积结构受外部环境的影响, 也是造成沉积物声速分布的复杂特征的重要因素, 因此不可能存在单一模型能够广泛适用于描述各种类型沉积物的声速分布规律。另一方面, 模型参数的选择多基于沉积物的孔隙性或者颗粒大小等物理因素, 而这些参数往往难以直接测量, 或无法测量, 部分参数甚至没有明确的物理意义, 大部分参数由均匀各向同性介质得到而又被运用到非均匀沉积物中。模型参数的选择一般采用曲线拟合和混合优化的方法; Stoll参数将模型参数分为砂质和泥质沉积物两类,均采用单数值形式; Schock参数把渗透率、孔隙因子和骨架体积模量等分别看作是孔隙度、粒径和有效压力的函数, 建立出这些未知参数的计算公式,这些模型参数选择和确定方法均得到了验证和应用。但对于复杂沉积环境中的沉积物, 其模型参数的选择仍需要基于大量的沉积物物理性质和声速测试, 按照沉积物类型和沉积环境等进行更为精细的分类, 并且考虑沉积物的孔隙形状、堆垒方式和矿物成分, 总结实测物理参数与无法测量的物理参数之间的函数关系, 代替利用单一数值表示整个区域沉积物的简化方法, 建立更精确的参数选择方法。

4 结论

通过对南海南部表层沉积物进行声学测量试验和利用声波传播理论进行声速计算, 对比了测量试验与三种理论模型的结果, 分析了该海域的声速空间变化特征, 得到以下认识:

(1)实测声速值与模型声速计算值的对比分析表明, Wood方程计算值与实测值的相对偏差较大, Biot-Stoll模型适合于陆架高声速区沉积物的声速预测, Buckingham模型适合于更广范围海域沉积物声速的计算。模型计算声速不能体现实测声速分布的复杂性和局部性。相比侧重于沉积物孔隙性的Biot-Stoll模型, 兼具流体和弹性固体双重性质的Buckingham模型更适用于解释该海域沉积物的声波传播特征。

(2)通过分析声速平面和垂向的变化特征, 表明沉积物实测声速的空间变化特征与沉积环境和物理性质具有相关性。由于压实作用而造成的声速垂向增大模式, 不能代表所有海域浅表层沉积物的声速结构。

(3)在确定模型的参数时, 由于模型涉及参数较多, 一些参数还仅依靠文献资料和值域范围进行优化拟合确定, 因此需要针对不同类型的海洋沉积物进行大量的物理性质和声速测试, 建立实测参数和未知参数的函数关系, 从而更精确的选择模型参数。Acknowledgements:

This study was supported by the Public Science and Technology Research Funds Projects of Ocean (Nos. 201405032 and 200905025), and the National Natural Science Foundation of China (No. 41330965).

参考文献:

陈静, 阎贫, 王彦林, 金丹, 林秋金. 2012. 基于Biot-Stoll模型声速反演中的参数选择——以南海南部沉积物为例[J]. 热带海洋学报, (1): 50-54.

付淑清, 朱照宇, 邱燕, 欧阳婷萍. 2008. 南海南部陆坡晚第四纪沉积环境变化[J]. 热带地理, 28(2): 99-102.

李傲仙, 李延河, 乐国良. 2005. 深海沉积物中碲异常的成因[J].地球学报, 26(S1): 186 - 189.

李赶先, 龙建军. 2014. 南海南部海域岛礁区海底珊瑚砂声速影响因素的初步研究[J]. 海洋学报, 36(5): 152-160.

杨涛, 薛紫晨, 杨竞红, 蒋少涌. 2003. 南海北部地区海洋沉积物中孔隙水的氢、氧同位素组成特征[J]. 地球学报, 24(6): 511-514.

张福生, 卢博, 李赶先, 黄韶健. 2001. 南沙群岛附近海域海底声学性质的分析与研究[J]. 湛江海洋大学学报, 21(S1): 116-122.

周丰年, 赵建虎, 周才扬. 2001. 多波束测深系统最优声速公式的确定[J]. 台湾海峡, 20(4): 411-419.

朱祖扬, 王东, 周建平, 王秀明. 2012. 基于非饱和Biot-Stoll模型的海底沉积物介质声频散特性研究[J]. 地球物理学报, 55(1): 180-188.

邹大鹏, 卢博, 阎贫, 吴百海. 2012a. 南海北部海底沉积物在温度变化下的三种声速类型[J]. 地球物理学报, 55(3): 1017-1024.

邹大鹏, 阎贫, 卢博. 2012b. 基于海底表层沉积物声速特征的南海地声模型[J]. 海洋学报: 中文版, 34(3): 80-86.

References:

BERRMAN J G. 1999. Origin of Gassmann’s equations[J]. Geophysics, 64: 1627-1629.

BIOT M A. 1956a. Theory of propagation of elastic waves in a fluid-saturated porous solid. I. Low frequency range[J]. J. Acoust. Soc. Am., 28: 168-178.

BIOT M A. 1956b. Theory of propagation of elastic waves in a fluid-saturated porous solid. II. Higher frequency range[J]. J. Acoust. Soc. Am., 28: 179-191.

BRIGGS K B, RICHARDSON M D. 1997. Small-scale fluctuations in acoustic and physical properties in surficial carbonate sediments and their relationship to bioturbation[J]. Geo-Marine Letters, 17(4): 306-315.

BUCKINGHAM M J. 1997. Theory of acoustic attenuation, dispersion, and pulse propagation in unconsolidated granular materials including marine sediments[J]. J. Acoust. Soc. Am., 102(5): 2579-2596.

BUCKINGHAM M J. 1998. Theory of compressional and shear waves in fluidlike marine sediments[J]. J. Acoust. Soc. Am., 103(1): 288-299.

BUCKINGHAM M J. 2005. Compressional and shear wave properties of marine sediments: comparisons between theory and data[J]. J. Acoust. Soc. Am., 117(1): 137-152.

CHEN Jing, YAN Pin, WANG Yan-lin, LIN Qiu-jin. 2012. Choice of Parameters for Biot-Stoll Model- based Inversion of Sound Velocity of Seafloor Sediments in the Southern South China Sea[J]. Journal of Tropical Oceanography, (1): 50-54(in Chinese with English abstract).

CHOTIROS N P, ISAKSON M J. 2004. A broadband model of sandy ocean sediments: Biot-Stoll with contact squirtflow and shear drag[J]. J. Acoust. Soc. Am., 116: 2011-2022.

FU Shu-qing, ZHU Zhao-yu, QIU Yan, OUYANG Ting-ping. 2008. The Changes of the Depositional Environment of the Southern South China Sea Continental Slope during Late Quaternary[J]. Tropical Geography, 28(2): 99-102(in Chinese with English abstract).

HAMILTON E L. 1971. Prediction of in-situ acoustic and elastic properties of marine sediments[J]. Geophysics, 36(2): 266-284.

HAMILTON E L. 1980. Geoacoustic modeling of the sea floor[J]. J. Acoust. Soc. Am., 68: 1313-1340.

HAMILTON E L, BACHMAN R T. 1982. Sound velocity and related properties of marine sediments[J]. J. Acoust. Soc. Am., 72: 1891-1904.

HAMILTON E L. 1985. Sound velocity as a function of depth in marine sediments[J]. J. Acoust. Soc. Am., 78: 1348-1355.

HOU Zheng-yu, GUO Chang-sheng, WANG Jing-qing, LI Hui-yin, LI Tie-gang. 2014. Tests of new in-situ seabed acoustic measurement system in Qingdao[J]. Chinese Journal of Oceanology and Limnology, 32(5): 1172-1178.

JACKSON D R, RICHARDSON M D. 2007. High-frequency seafloor acoustics[M]. New York, NY, USA: Springer Science + Business Media.

LI Ao-xian, LI Yan-he, YUE Guo-liang. 2005. The Cause for Tellurium Enrichment in Deep-Sea Sediments[J]. Acta Geoscientica Sinica, 26(S1): 186-189(in Chinese with English abstract).

LI Gan-xian, LONG Jian-jun. 2014. A preliminary study of the sound velocity influence factors of submarine coral sand of islands sea area in southern South China Sea[J]. Acta Oceanologica Sinica, 36(5): 152-160(in Chinese with English abstract).

LIU Bao-hua, HAN Tong-cheng, KAN Guang-ming, LI Guan-bao. 2013. Correlations between the in situ acoustic properties and geotechnical parameters of sediments in the Yellow Sea[J]. China. J. Asian Earth Sci, 77: 83-90.

LIU Jian-guo, XIANG Rong, CHEN Zhong, CHEN Mu-hong, YAN Wen, ZHANG Lan-lan, CHEN H. 2013. Sources, transport and deposition of surface sediments from the South China Sea[J]. Deep Sea Research Part I: Oceanographic Research Papers, 71: 92-102.

LU Bo, HUANG Shao-jian, LI Gan-xian, ZHANG Fu-sheng. 2003. Vertical variations of core sound velocity: Evidence of paleooceanographic history since the Pleistocene epoch[J]. Marine Georesources and Geotechnology, 21(2): 63-71.

LU Bo, LIU Qiang, LI Gan-xian. 2010. Grain and pore factors in acoustic response to seafloor sediments[J]. Marine Georesources and Geotechnology, 28(2): 115-129.

SCHOCK S G. 2004. A method for estimating the physical and acoustic properties of the sea bed using chirp sonar data[J]. IEEE Journal of Oceanic Engineering, 29(4): 1200-1217.

STOLL R D. 1989. Sediment Acoustics[M]. New York: Lecture Notes in Earth Sciences, Springer-Verlag.

STOLL R D, BAUTISTA E O. 1998. Using the Biot theory to establish a baseline geoacoustic model for seafloor sediments[J]. Continental shelf research, 18(14): 1839-1857.

WANG Jing-qiang, GUO Chang-sheng, HOU Zheng-yu, FU Yong-tao, YAN Jun. 2014. Distributions and vertical variation patterns of sound speed of surface sediments in South China[J]. Sea. J. Asian Earth Sci., 89: 46-53.

WILLIAMS K L, JACKSON D R, THORSOS E I, TANG D J, SCHOCK S S. 2002. Comparison of sound speed and attenuation measured in a sandy sediment to predictions based on the Biot theory of porous media[J]. IEEE Journal of Oceanic Engineering, 27(3): 413-428.

YANG Tao, XUE Zi-chen, YANG Jing-hong, JIANG Shao-yong. 2003. Oxygen and Hydrogen Isotopic Compositions of Pore Water from Marine Sediments in the Northern South China Sea[J]. Acta Geoscientica Sinica, 24(6): 511-514(in Chinese with English abstract).

ZHANG Fu-sheng, LU Bo, LI Gan-xian, HUANG Shao-jian. 2001. A Study on the Seafloor Sediments Acoustic Characteristics of Nansha Islands Sea Area[J]. Journal of Zhanjiang Ocean University, 21(Sl): 116-122(in Chinese with English abstract).

ZHOU Feng-nian, ZHAO Jian-hu, ZHOU Cai-yang. 2001. Determination of Classic Experiential Sound Speed Formulae in Multibeam Echo Sounding System[J]. Journal of Oceanography in Taiwan Strait, 20(4): 411-419(in Chinese with English abstract).

ZHOU Zu-yang, WANG Dong, ZHOU Jian-ping, WANG Xiu-ming. 2012. Acoustic Wave Dispersion and Attenuation in Marine Sediment Based on Partially Gas-saturated Biot-Stoll Model[J]. Chinese J. Geophys., 55(1): 180-188(in Chinese with English abstract).

ZOU Da-peng, LU Bo, YAN Pin, WU Bo-hai. 2012. Three Kinds of Acoustic Speeds of Seafloor Sediments in the Northern South China Sea with Temperature Variation[J]. Chinese J. Geophys, 55(3): 1017-1024(in Chinese with English abstract).

ZOU Da-peng, YAN Pin, LU Bo. 2012. A Geoacoustic Model Based on Sound Speed Characteristic of Seafloor Surface Sediments of the South China Sea[J]. Acta Oceanologica Sinaica, 34(3): 80-86(in Chinese with English abstract).

Sound Speed Distribution of Seafloor Sediments in Nansha Islands Sea Based on Buckingham Model and Biot-Stoll Model

WANG Jing-qiang1, 4), GUO Chang-sheng2, 4)*, LIU Bao-hua3, 4), CHEN Wen-jing2, 5), HOU Zheng-yu2, 5), HAN Guo-zhong1, 4)
1) Key Laboratory of Marine Sedimentology and Environment Geology, First Institute of Oceanography,
State Oceanic Administration, Qingdao, Shandong 266061; 2) Key Laboratory of Marine Geology and Environment, Institute of Oceanology, Chinese Academy of Sciences, Qingdao, Shandong 266071; 3) National Deep Sea Center, State Oceanic Administration, Qingdao, Shandong 266061; 4) Laboratory for Marine Geology, Qingdao National Laboratory for Marine Science and Technology, Qingdao, Shandong 266061; 5) University of Chinese Academy of Sciences, Beijing 100049

Abstract:In order to analyze the application of the speed theoretical models to predicting the sound speed of sediments in the southern South China Sea, the authors calculated the sound speed by using Wood equation, Buckingham model, and Biot-Stoll model respectively. The comparison between the calculated and the measured sound speeds shows that the average deviation between the calculated sound speeds with Buckingham model and the measured sound speeds is smaller than the calculated values with Wood equation and Biot-Stoll model. The comparison of the sound speed ratio distributions indicate that the calculated sound speed ratios with Buckingham model and Biot-Stoll model have the similar horizontal distributions with the measured sound speed ratios. Thesound speeds have different horizontal distributions in different sedimentary environments and are closely related to the physical properties and the deposition of sediments. The calculated sound speed ratios are invariant with the depth, while the measured values have different vertical distributions in several different geomorphic units. According to the comparison results, the Biot-Stoll model is only suitable for the coarse sediments in the continental shelf, and the Buckingham model is more applicable to predicating the sound speed of sediments in the study area. The research is significant in obtaining the sound speed distribution of the sediments in the southern South China Sea, and can provide reference for the multi-beam echo sounding and the sub-bottom survey.

Key words:seafloor sediment; Buckingham model; Biot-Stoll model; sound speed distribution; sound speed ratio

中图分类号:O422.1; O424

文献标志码:A

doi:10.3975/cagsb.2016.03.13

收稿日期:2016-02-19; 改回日期: 2016-03-25。责任编辑: 魏乐军。

第一作者简介:王景强, 男, 1989年生。博士后。主要从事海洋沉积声学研究。E-mail: wang_jingqiang@aliyun.com。

*通讯作者:郭常升, 男, 1964年生。研究员。主要从事海洋地质声学和海洋地球物理研究。E-mail: guochine@qdio.ac.cn。