高速公路机电设备维修备件需求预测方法

郭琼琼，邢国英，王　沛，祝日星

(1.河南省交通运输厅高速公路少林寺至新乡管理处，郑州　450000； 2.长安大学，西安　610064)

高速公路机电设备维修备件需求预测方法

郭琼琼1，邢国英1，王沛2，祝日星2

(1.河南省交通运输厅高速公路少林寺至新乡管理处，郑州450000； 2.长安大学，西安610064)

摘要：对高速公路机电设备维修备件的需求进行连续型和间断型预测分析。连续型需求预测采用指数平滑法和移动平均法，间断型需求预测采用贝叶斯预测法。2种方法均能准确预测维修备件的需求，有助于确定备件的合理储备量和制定科学的采购计划，从而在保障企业运营安全和高服务水平的同时，有效降低运营成本，节省流动资金。

关键词：高速公路；机电设备；维修备件；需求预测

高速公路机电设备维修备件是高速公路安全畅通运营的有力后勤保障和支持。当机电设备发生故障时，其能够保证设备得到及时维修，避免设备故障带来的运营损失和安全隐患。合理地储备维修备件可以有效减少企业的流动资金占用率和降低运营成本，但管理人员往往很难确定最佳的库存储备，只有准确预测维修备件的消耗趋势，才能确定合理的库存储备量，帮助库存管理人员制定库存采购计划[1]。因此，高速公路维修备件的需求预测对高速公路管理企业具有重要意义。

本文针对高速公路维修备件连续型和间断型需求采用不同的方法分别进行预测，并用误差分析方法对需求预测结果的准确性进行检验。

1需求预测方法及步骤

备件需求预测指在收集库存备件相关的历史数据进行分析的同时，采用预测理论方法，对库存备件未来的需求变化趋势和需求量进行合理预估[2]。

根据需求预测结果可以将预测方法分为定量和定性的方法。按时间跨度可将预测方法分为短期、中期和长期方法。

备件需求预测基本步骤如图1所示，包括如下内容。

1) 明确本次备件需求预测的目标，及预测期望能达到的准确度。

2)收集并整合影响预测结果的资料精度。资料包括备件消耗记录，设备历史故障率。

图1　备件需求预测基本步骤

3) 选取预测模型与方法时，需分析现有数据资料及备件的消耗特点，选择合适的数学模型和方法进行预测。

4) 将预测值与实际值进行对比，若误差较大，则需分析总结误差较大的原因，及时修正模型，重新调整计算。

5) 若预测结果误差满足要求，可认为预测方法准确。

2高速公路维修备件需求预测

2.1连续型需求预测

高速公路维修备件的需求随时间变化具有一定连续性，可使用时间序列方法和回归分析法来预测[3]。回归分析法是基于大量观察数据分析求解出与需求有关的变量与需求之间线性方程的参数并进行预测，而实际上对维修备件的需求影响因素很多，如备件寿命、装机量、设备维修方式、外界因素损坏等。这些因素有的很难进行量化和统计，因此主要使用时间序列方法对连续型备件的需求进行预测。

采用时间序列法[4]进行预测时，只需知道要预测的需求量在历史上的一系列观察值，并分析其规律，再把规律外推至预测期，便可获得需求量的预测值。

移动平均法是最简单的一种时间序列预测法，其含义是预测值近似等于最近N次供应周期的需求量平均值[5]。使用移动平均法时，需在已知t时刻前N次需求量的情况下，对t时刻需求量Ft进行预测，公式如下：

(1)

式中：Dt-1，Dt-2，...，Dt-N分别表示t时刻前的第一次需求量，第二次需求量及第N次需求量。

该方法适用于平稳时间序列的短期预测。一般来说，移动时间越长，时间序列被修匀的效果越显著，对随机因素引起的波动剔除就更彻底，但随着移动时间加长，所需资料也越多。

指数平滑法是一种重要的时间序列预测法，其精度相对较高，且算式也很简单，所以被广泛应用。该方法认为时间序列态势具有稳定性，且对时间序列进行合理的顺势外延后即可得到未知的预测值。该方法不舍弃过去的预测数据，但会随着时间推移越早数据对未来预测值的影响越小[6-7]。指数平滑法计算公式为：

(2)

从公式(2)可以看出，只要给出t阶段的预测值，就可以算出t+1阶段的预测值，以前其他阶段的实际值都无需保留。

2.2间断型需求预测

高速公路机电设备维修备件中较重要设备的需求量往往较小，这些设备通常在很长时间内运行良好，可能1～2年或更长时间都不需要更换，故其需求表现为一种间歇性。对高速公路需求频率较低的这类维修备件使用前述连续型预测方法很难获得好的预测效果，因此本文使用贝叶斯预测法进行预测。

贝叶斯预测方法[8]是基于贝叶斯统计的一种数学模型。其进行统计推断时，不仅考虑了总体信息和样本信息，还考虑了先验信息以提高统计推断的质量。贝叶斯预测基本模式如图2示。

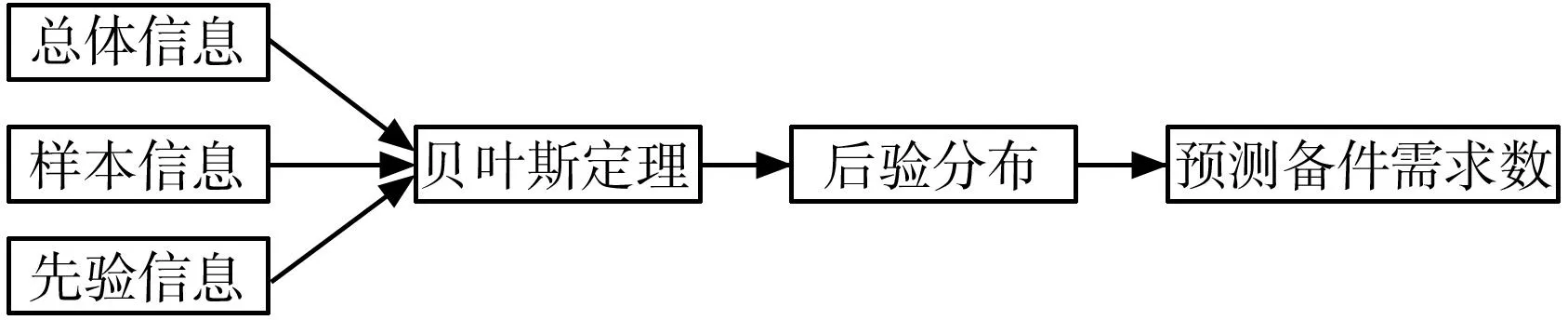
图2　贝叶斯预测基本模式

使用贝叶斯预测方法时，有以下几个步骤。

1) 确定需求量的概率密度分布。

高速公路维修备件消耗规律基本符合泊松分布，其分布函数P表达式如下：

(3)

式中：i为高速公路维修备件消耗量；S为备件需求量；n为备件装机量；λ0为备件故障率初始估计值。

2) 确定先验分布及其参数。

采用贝叶斯方法处理时存在共轭分布现象。泊松分布的共轭分布是伽玛分布，其形状参数为α，尺度参数为β，α和β即为先验分布密度函数的超参数值。

先验分布π服从Ga(α,β)的伽玛分布，表达式如下：

(4)

利用先验信息可获得先验分布的均值ωλ0和分位数δλ0，且通过如下方程组可计算先验分布的参数。

(5)

式中：λ为高速公路某一备件的实际故障率。

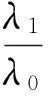
3) 计算后验分布及其参数。

由密度函数可知，在预测周期L内，发生k次故障时先验分布公式为：

(6)

贝叶斯公式后验分布形式为：

(7)

式中：θ仅表示一个参数；x1,x2...xn表示样本。

将式(4)和(6)代入式(7)中计算，可以得到后验分布的概率密度为：

(8)

由式(8)可以看出，后验分布服从Ga(α+k,β+nL)的伽玛分布，如果在时间t周期内观察到r次故障，则λ的先验分布密度函数可变为π(λ|α′,β′)。其中，α′和β′为更新后先验密度函数的超参数，可用公式α′=α+r，β′=β+tn进行计算。

4) 确定备件的需求量。

确定了超参数后，L周期内满足服务水平为P的需求备件库存数S便可以利用式(9)求出：

(9)

3需求预测实例分析

3.1连续型预测分析

通过对某省高速公路机电设备维修备件的实际调研，得到了需求较稳定且零需求很少的连续型需求备件需求量在2012年12个月的历史需求数据。

采用指数平滑法和移动平均法并应用Excel软件分别对该备件1年的需求量进行预测计算。当平滑系数为0.1时，维修备件的需求预测结果见表1。

表1　指数平滑法预测结果

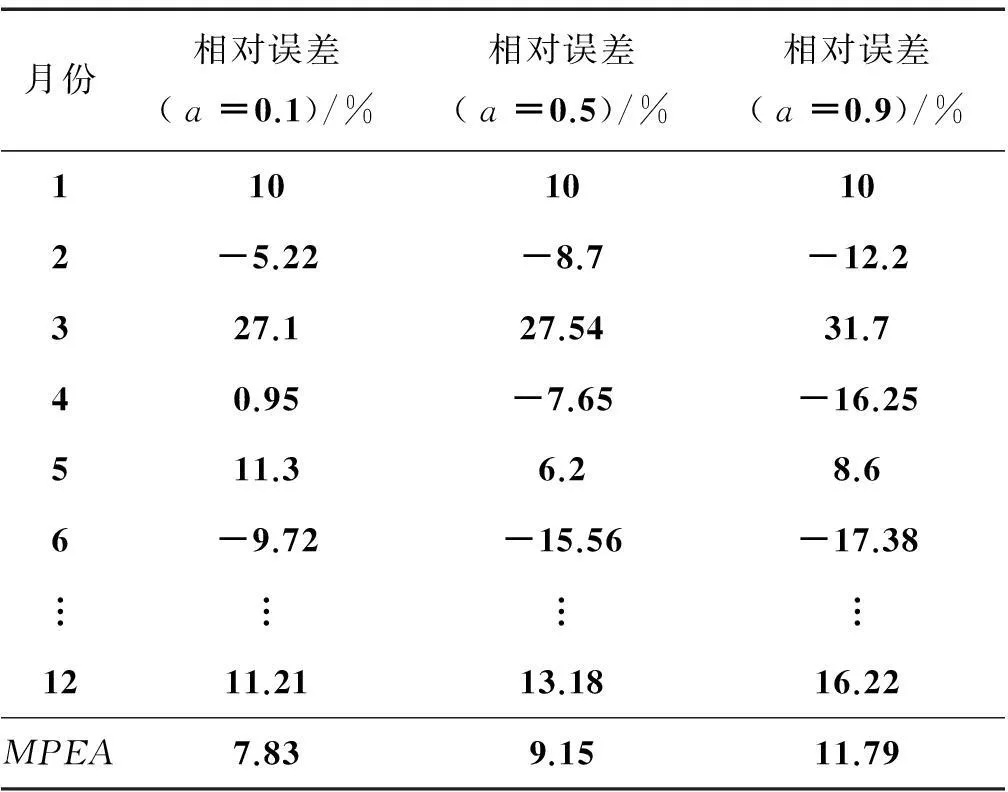
表2　采用3种不同平滑系数的预测结果分析

由表2数据可以看出，平滑系数a越小，预测值就越不容易受到近期偶然波动的干扰。当a=0.1时，平均相对误差的绝对值MPEA=7.83%，属于高精度预测结果。

采用步长为3的移动平均法进行需求预测值进行分析，结果如表3所示。

使用平均相对误差的绝对值可以得到步长为3的移动平均预测方法的MEPA=7.53%，同样可以计算步长为5的移动平均预测法的MEPA=5.79%。由此可以看出，随着步长的增加，时间序列被修正的效果越好，但步长增加需要的历史数据也就越多，例如移动平均法步长为5则需要前5个月的历史数据才能预测后面的7个月的值，而步长为3时则只需要前3个月的历史数据。

表3　移动平均法(步长为3)预测结果

综上所述，预测某一连续型备件的需求时，如果该备件的历史数据较多，则使用步长为5的移动平均法；若数据较少，则使用步长为3的移动平均法或平滑系数a=0.1的指数平滑法，以获得较好的预测结果。

3.2间断型预测分析

通过对某省高速公路机电设备维修备件的实际调研，得到2种维修备件A和B在2011年及2012年共8个季度的实际维修需求，见表4。本文根据2种备件前7个季度的实际维修需求，采用贝叶斯预测方法对第8个季度的需求进行预测，并将预测结果和第8个季度的实际维护需求进行对比。

表4　2种备件的季度维修情况

注：1、2、3、4表示一年当中的4个季度。下同。

采用贝叶斯预测方法对2种备件第8个季度的需求进行预测时，步骤如下。

1) 计算备件故障率初始估计值λ0和各观察周期内的故障率λ1，并求得二者的比值。备件初始故障率值λ0=平均故障数/安装数；观察期内故障率λ1=各季度的故障数/安装数。由表4数据可以计算得到λ1和λ0的值，即可得2种备件的λ1/λ0值，见表5。

2) 计算ω和δ的值。ω为多个λ1/λ0的平均值，计算时需考虑前7个数据。δ为服务水平P与选取数据的周期数N的乘积取整后所对应的由小到大的那个λ1/λ0值。本文选择服务水平为95%，则2种备件的δ值为从小到大第6(0.95×7=6)个λ1/λ0值，分别为δ1=1.273，δ2=1.904 8。计算后得到的各参数值见表6。

3) 利用公式(8)和超参数更新公式可分别计算2种备件后验分布新的超参数α'和β，见表7。

将表7中更新后的超参数带入公式(9)，可求解得出2种备件第8个季度的需求量预测结果，见表8。

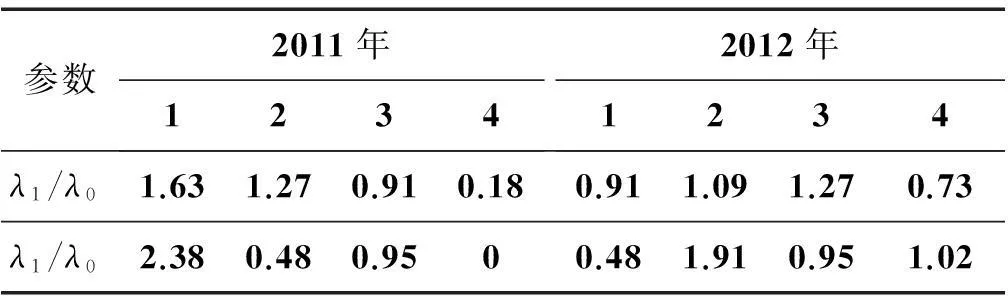
表5　2种备件的λ1/λ0值

表6　2种备件的各参数值

表7　贝叶斯预测的超参数和其更新值

表8　2种备件第8个季度的需求量预测结果

将预测值与2012年第4季度的实际值进行分析比较，可以看出，贝叶斯预测法的结果误差较小，用于需求间断的维修备件需求预测是可行的。

4结束语

本文将高速公路机电设备维修备件的需求分为连续型和间断型，分别采用不同方法对维修备件的需求进行预测，并基于预测结果的误差分析，选择合适的预测方法，为高速公路机电设备维修备件需求预测和采购计划的制定提供了科学和有效的理论支持。

参 考 文 献

[1]赵卉.关键维修备件的库存管理刍议[J]．研究探讨，2014(11)：99-100.

[2]颜文燕. 基于需求预测的S公司备件管理研究[D].广州：华南理工大学，2012.

[3]黄照协.备件消耗预测方法研究现状及发展[J]．舰船电子工程，2015(1)：14-18.

[4]柳青，王肖.维修备件需求预测方法研究[J].科学时代，2012(9)：1-8.

[5]苗濛.备件需求预测模型研究[J]．物流技术，2013(11)：78-79.

[6]吴静怡，李红卫，张居梅，等.基于指数平滑法的光纤通信传输设备维修备件需求预测[J]．物联网技术，2015(12)：40-42.

[7]任喜.两步法与指数平滑法分析研究[J]．计算机与数字工程，2014(11)：2063-2065.

[8]茆诗松，汤银才. 贝叶斯统计[M].北京：中国统计出版社，2012.

Prediction Methods for Demand of Maintenance Spare Parts of Electromechanical Equipment for Expressways

GUO Qiongqiong1, XING Guoying1, WANG Pei2, ZHU Rixing2

Abstract:This paper conducts continuous and intermittent predication analysis for the demand of maintenance spare parts of electromechanical equipment for expressways. The continuous demand prediction adopts the exponential smoothing method and the moving average method, and the intermittent demand predictions adopts the Bayesian prediction method. These methods can predict the demand of maintenance spare parts accurately and are helpful for determining reasonable reserves of spare parts and laying down scientific procurement plans so as to reduce operating costs and save liquid capitals effectively while guaranteeing operating safety and high service level of the enterprise.

Keywords:expressway; electromechanical equipment; maintenance spare part; demand prediction

DOI:10.13607/j.cnki.gljt.2016.03.026

基金项目：河南省交通运输厅科技计划项目(2014G23-2)；中央高校基本科研业务费专项资金资助项目(2013G3324005)

收稿日期：2015-11-25

作者简介：郭琼琼(1984-)，男，河南省郑州市人，本科，助工。

文章编号：1009-6477(2016)03-0117-05中图分类号：U412.36+6

文献标识码：B