广义随机仿射系统的线性二次控制

朱怀念, 张成科, 曹　铭, 宾　宁

(广东工业大学 1.经济与贸易学院; 2.管理学院，广东 广州 510520)

广义随机仿射系统的线性二次控制

朱怀念1, 张成科1, 曹铭2, 宾宁2

(广东工业大学 1.经济与贸易学院; 2.管理学院，广东 广州 510520)

摘要:研究了一类连续时间广义随机仿射系统的线性二次(Linear Quadratic, LQ)控制问题.在定义了广义随机系统稳定性的相关概念后，通过一个线性矩阵不等式(Linear Matrix Inequality, LMI)给出了系统稳定性的条件.然后，利用Riccati方程法分别研究了有限时间广义随机仿射系统的LQ问题和无限时间广义随机系统的LQ问题，得到了有限时间最优反馈控制的存在条件等价于一个推广的微分Riccati方程和一个推广的倒向微分方程存在解，而对应的无限时间最优反馈控制的存在条件等价于一个推广的代数Riccati方程存在解，同时给出了最优反馈控制的显式表达及最优性能指标值.

关键词:广义随机仿射系统; 线性二次控制; 线性矩阵不等式; Riccati方程

广义系统[1]是一类更一般化且具有广泛应用背景的动力系统，大量出现在许多实际的系统模型中，如电力系统、经济系统、受限机器人、电子网络和宇航系统等[2]，所以对它的研究具有重要的理论意义和实用价值，迄今为止已取得了丰硕成果[3-4].同时，现实世界中的许多系统都不可避免地存在不确定性，这些不确定性影响到人类为寻找最优结果而付出的努力，因而随机系统的研究也引起了学术界越来越多的关注[5-10].

近年来，将两者结合起来的广义随机系统成为了控制领域的一大研究热点[11-15].文献[11-12]分别讨论了连续时间广义混杂系统的稳定性和镇定性，文献[13]基于广义混杂系统的稳定性结果，提出了广义线性随机混杂系统均方稳定的判定定理，文献[14]对文献[13]的结果进行了改进，得到了连续时间和离散时间广义线性It随机系统稳定性的充分条件，文献[15]研究了连续时间广义线性It随机系统的稳定性和LQ控制问题.

纵观以上文献发现，广义随机系统的稳定性分析已经取得到较丰富的成果，但关于广义随机仿射系统LQ控制的研究还比较少.而随机仿射系统的LQ控制问题有着强大的应用背景，一个典型的例子就是基于随机LQ框架的连续时间均值-方差型投资组合选择问题，通过构造一个辅助问题，可以将该问题转化为求解一个随机仿射系统的LQ控制问题，详细分析见文献[8].另一个典型的应用就是主-从随机LQ微分博弈问题，详细分析见下一节的研究动机部分.此外，当利用随机线性系统的LQ控制去逼近求解随机非线性系统的最优控制策略时，随机仿射系统的LQ控制也发挥着重要的作用.

本文在文献[12]和[14]有关广义随机系统稳定性分析的基础上，研究广义随机仿射系统的LQ控制问题.一方面将文献[6]中正常线性It随机系统的LQ控制问题拓展到广义随机仿射系统的LQ控制中；另一方面将文献[15]中广义线性It随机系统LQ控制的相关结果推广至广义随机仿射系统中，同时也指出了文献[15]中有待改进的地方并给出了解释，因而本文的工作有着较好的理论意义和现实应用价值.

1预备知识

1.1研究动机

考虑有限时间广义主-从(leader-follower)随机LQ微分博弈问题，博弈系统的动态方程为

(1)

其中E是rank(E)=r≤n的n-阶常数矩阵；A(·)、B1(·)、B2(·)、C(·)、D1(·)和D2(·)是具有适当维数的有界矩阵；x(·)∈n为状态过程；u1(·)和u2(·)是两个容许控制过程，表示博弈人1(记为从者，follower)和2(记为主者，leader)的控制策略，其允许策略集合分别记为U1[0,T]m1)和U2[0,T]m2)；W(·)是定义在完备概率空间(Ω,F,{Ft}t≥0,P)上的一维标准布朗运动.博弈人的性能指标定义为

(2)

其中Qi(·)∈j.

在广义主-从随机LQ微分博弈问题中，博弈人i的目标是通过选取控制策略ui(·)∈Ui[0,T]使性能指标Ji(x0;ui(·),uj(·))最小化.进一步，为了得到该博弈问题的均衡解，可将该问题转化为求解下述两个随机LQ问题来实现.

LQ问题1：给定博弈人2的控制策略u2(·)∈U2[0,T]，对于固定的x0∈n，博弈人1选择u1(·)∈U1[0,T]，使得).LQ问题2：当博弈人1选择了其最优策略后，博弈人2选择u2(·)∈U2[0,T]，使得

其中f(·)=B2(·)u2(·)，g(·)=D2(·)u2(·)，这是一个典型的广义随机仿射系统的LQ问题.当从者得到其最优控制策略后，将最优控制策略代回博弈系统的动态方程(1)，求解主者最优控制策略的LQ问题2也是一个广义随机仿射系统的LQ问题.当E=I时正常系统的主-从随机LQ微分博弈问题，详细分析见文献[16]，而一般系统的主-从随机微分博弈问题，见文献[17]的详细论述.

1.2记号和一些有用的引理

令(Ω,F,{Ft}t≥0,P)是一个完备概率空间，其上定义了一个标准布朗运动{W(t)}t≥0，{Ft}t≥0为{W(t)}t≥0生成的自然信息流.对固定的T>0，定义下面的空间：

此外，为了表述的方便，在全文中引入下面记号：

MT：矩阵或向量M的转置；Tr(M)：矩阵M的迹；det(M)：矩阵M的行列式；deg(f)：多项式f的次数；n×m：n×m阶矩阵的全体；Sn：n×n阶对称矩阵的全体；：n×n阶非负定对称矩阵的全体；阶正定对称矩阵的全体；(0,T;X)：Banach空间上定义在[0,T]上X-值连续函数的全体.

考虑下式描述的广义随机系统

(4)

为了保证系统(4)解的存在唯一性，引入下面的引理.

引理1[14]如果存在一对非奇异矩阵M∈n×n和N∈n×n，使得对三元组(E,A,F)，下述至少一个条件成立时，则式(4)存在唯一解.

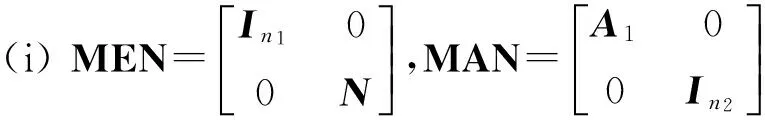
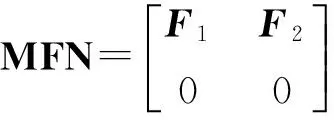
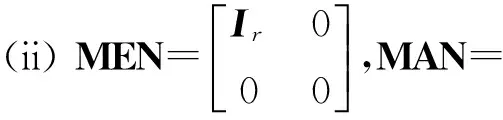
其中A1,F1∈r×r，F2∈r×(n-r)，F3∈(n-r)×(n-r).

在控制理论中，系统的稳定性是一个非常重要的概念，它是系统能否正常工作的最基本条件，因而在研究广义随机仿射系统LQ控制问题之前，我们先给出有关系统稳定性的一些定义和引理.

定义1[14]对于系统(4)

(i) 如果存在常数s，使得det(sE-A)≠0，则称系统(4)是正则的；

(ii) 如果deg(det(sE-A))=rank(E)，则称系统(4)是无脉冲的；

(iii) 如果对于任意的允许初态x0∈n，系统(4)的解x(t)满足‖x(t)‖2=0，则称系统(4)是渐近均方稳定的；

(iv) 系统(4)是渐近均方容许的，如果它是正则、无脉冲且渐近均方稳定的.

引理2[18]设一个n-维过程x(·)满足随机微分方程

dx(t)=f(t,x(t))dt+g(t,x(t))dW(t).

给定V(t,x(t))∈2([0,T]×n)，则有

dV(t,x(t))=ΓV(t,x(t))dt+

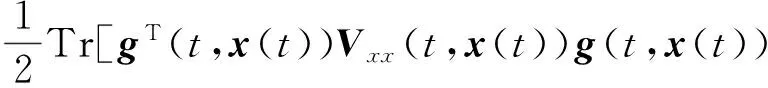
下述引理给出了系统(4)稳定的条件，同时修正了文献[15]中的定理 3.1.

引理3如果存在一个非奇异对称矩阵P，使得下述LMI成立

ATPE+ETPA+FTPF<0,

(5)

则系统(4)是渐近均方容许的.

证明 首先选取形如

V(x(t))=xT(t)ETPEx(t)

的Lyapunov函数V，然后采取文献[19]中的分析方法，不难得到系统(4)满足正则、无脉冲和渐近均方稳定的条件，即系统(4)是渐近均方容许的.引理1证毕.

d(xT(t)ETP(t)x(t))=d(xT(t)ET)P(t)x(t)+xT(t)PT(t)d(Ex(t))+d(xT(t)ET)P(t)d(x(t)).此时取而代之的V应该是

V(x(t))=xT(t)ETPEx(t).

2有限时间随机LQ问题

2.1问题描述

考虑如下的广义受控系统：

(6)

其中E是rank(E)=r≤n的n-阶常数矩阵；x0∈n是给定的初始状态；m)是一个容许控制过程，其允许策略空间记为Uad.

对每一个(x0,u(·))∈n×Uad，引入经典的二次型性能指标：

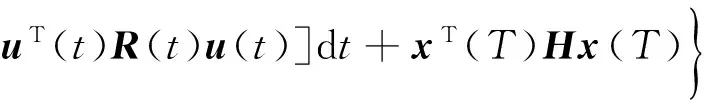
(7)

方程(6)的解x(·)称为控制u(·)∈Uad的响应，(x(·),u(·))称为一个容许对.最优控制问题的目标是对任意给定的x0∈n，通过寻找容许控制u(·)∈Uad，最小化性能指标JT(x0;u(·)).

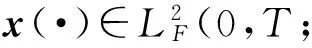
2.2主要结果

首先引入一个关于P(·)的推广的微分Riccati方程

(8)

和一个关于φ(·)的推广的倒向微分方程

(9)

下述定理给出了有限时间随机LQ问题的主要结果.

u*(t,x)=-K-1(t)[L(t)x(t)+h(t)].

(10)其中L(t)=BT(t)P(t)E+DT(t)P(t)C(t)，h(t)=BT(t)φ(t)+DT(t)P(t)g(t)，最优性能指标为

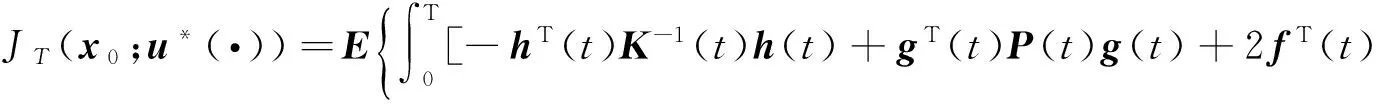
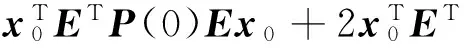
(11)

证明使用配方法证明，取

V(t,x(t))=xT(t)ETP(t)Ex(t)+2xT(t)ETφ(t)，

对xT(t)ETP(t)Ex(t)和2xT(t)ETφ(t)分别使用It公式，得

(12)

(13)

将式(12)和式(13)相加，得

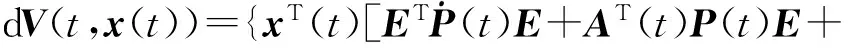
(14)

式(14)在[0,T]上积分，取数学期望，并结合式(7)得

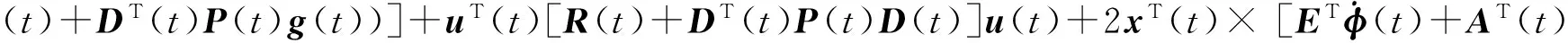
(15)

K(t)=R(t)+DT(t)P(t)D(t)>0，

ETP(T)E=H，ETφ(T)=0，

则最优反馈控制和最优性能指标分别为

u*(t,x)=-K-1(t)[L(t)x(t)+h(t)].

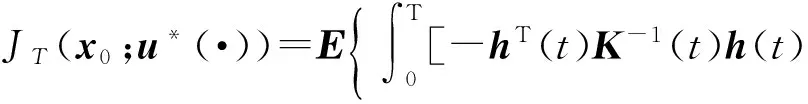
将最优反馈控制u*(t,x)代入式(6)中得

定理1得证.

注2若E=I，随机LQ问题(6)～(7)退化为一般意义下的线性It系统的随机LQ问题，该问题首次被Chen和Zhou[6]讨论，因而定理1是文献[6]中Theorem 3.1的拓展.

注3定理1是在假设式(6)-(7)中各系数不包含ω时得到的，当它们包含ω时，即A(·)=A(·,ω)，…，定理1则不再成立.理由如下：当A(·)=A(·,ω)，…时，我们对V(t,x(t))需作下述形式的假设：

V(t,x(t))=xT(t)ETP(t)Ex(t)+2xT(t)ETφ(t),

其中的ETP(t)E和ETφ(t)满足下述随机微分方程

dETP(t)E=Z(t)dt+Λ(t)dW(t),dETφ(t)=Θdt+ΨdW(t),t∈[0,T].

此时仅对xT(t)ETP(t)Ex(t)进行It微分，就可发现式(16)最后两项中的dx(t)无法计算，

d(xT(t)ETP(t)Ex(t))=

d(xT(t)ET)P(t)Ex(t)+

xT(t)d(ETP(t)E)x(t)+

xT(t)ETP(t)d(Ex(t))+

d(xT(t))ETP(t)Ed(x(t))+

d(xT(t))d(ETP(t)E)x(t)+

xT(t)d(ETP(t)E)d(x(t)).

(16)

因而定理1不再成立.

3无限时间随机LQ问题

3.1问题描述

无限时间情形下广义系统的随机LQ问题在文献[15]的第4.2部分已经被讨论过，考虑到该文中的部分结果有表述不准确的地方(详见下文的分析)，在本部分仍考虑文献[15]描述的受控系统：

对系统(17)，考虑下述形式的状态反馈控制

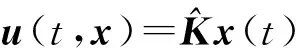
(18)

将式(18)代回式(17)，得到相应的闭环系统

(19)

定义2系统(17)称为渐近均方稳定的，如果存在一个形如式(17)的状态反馈控制，使得闭环系统(19)是渐近均方稳定的.

对每一个(x0,u(·))∈n×U(x0)，相应的二次型性能指标为

(20)

其中Q∈Sn，R∈Sm为已知的常数矩阵.再次强调，我们对式(20)中的状态权矩阵Q和控制权矩阵R未做任何限定，即R是不定的.

注意到系统(17)中的C≠0，D≠0，此时系统的扩散项中同时包含状态和控制，即噪声依赖于状态和控制，这在数理金融学中是常见的，尤其是基于随机LQ框架下的连续时间均值-方差型投资组合选择问题，见Zhou和Li[8].而当C=D=0时，系统(17)退化为一个确定性线性系统.我们知道，对于确定性系统的LQ问题，为了保证所研究问题的适定性，需要限定性能指标中的控制权矩阵R正定，状态权矩阵Q非负定，用数学语言描述即为：

(21)

利用配方法，取V(t,x(t))=xT(t)ETPx(t)，其中P∈n×n，满足ETP=PTE.V(t,x(t))对时间t求导得

2uT(t)BTPx(t).

上式先在[0,∞)上积分，然后加到式(21)的二次型指标中，经过运算得到下述受限的代数Riccati方程

(22)

注4在推导式(22)时，构造的V(t,x(t))与文献[12]研究连续时间混杂系统稳定性时构造的Lyapunov函数形式是一致的，且与文献[15]的式(25)不同，在文献[15]中，V(t,x(t))=xT(t)ETPEx(t)，进而使得式(25)和最优反馈控制均与奇异矩阵E有关，这也在一定程度上反映了随机系统和确定性系统之间的差别.

本部分考虑的最优控制问题是对任意给定的初始值x0∈n，通过寻找容许控制u(·)∈U(x0)，最小化性能指标J∞(x0;u(·)).

在给出主要结果之前，给出无限时间LQ问题的一个标准假设[9]：

假设1系统(17)是均方能稳的.

3.2主要结果

类似于上一节得到的有限时间随机LQ问题的相关结果，我们得到无限时间随机LQ问题的主要结果如下定理2所示.

定理2在假设1成立的条件下，若下述推广的代数Riccati方程存在解P∈Sn，

(23)

则无限时间随机LQ问题(17)-(20)的最优反馈控制和最优性能指标分别为

(24)

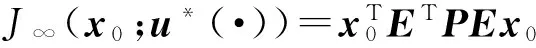
(25)

证明 假设存在P∈Sn满足式(23)，取V(t)=xT(t)ETPEx(t)，对V(t)使用It公式得

dV(t)=d(xT(t)ET)PEx(t)+

xT(t)ETPd(Ex(t))+d(xT(t)ET)Pd(Ex(t))=

{uT(t)DTPDu(t)+xT(t)(-Q+LTK-1L)x(t)+

2uT(t)Lx(t)}dt+{…}dW(t),

(26)

其中L=BTPE+DTPC.

由假设1知Ε[V(∞)]=0，将式(26)在[0,∞)上积分，取数学期望，再结合式(20)得

(27)

由式(27)容易得到最优反馈控制和最优性能指标分别为

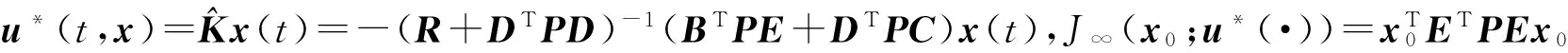
定理2得证.

注5定理2中的式(23)与文献[15]中的式(26)是不同的，之所以这样是因为在结合式(17)对V(t)使用It公式时，用的是[Cx(t)+Du(t)]TP×[Cx(t)+Du(t)]，而文献[15]使用的是[Cx(t)+Du(t)]TETPE[Cx(t)+Du(t)]，因而得到的代数Riccati方程和最优反馈控制均存在差别.

注6根据LMI理论，式(23)的解可通过求解一个等价的LMIs来得到

(28)

根据文献[7]的定理 13，式(28)等价于求解下述半定规划问题

(29)

而上述半定规划问题在Matlab中已有现成的工具包可供使用，因而式(23)是容易求解的.

4结论

本文针对一类连续时间广义随机仿射系统讨论了其线性二次控制问题，在引入广义随机系统的稳定性概念后，通过一个LMI给出了广义随机系统的稳定性条件.然后，借助Riccati方程法得到了有限时间广义随机仿射系统LQ问题最优反馈控制的存在条件等价于一个推广的微分Riccati方程和一个倒向微分方程存在解，而对应的无限时间广义随机系统LQ问题最优反馈控制的存在条件等价于一个推广的代数Riccati方程存在解，并给出了最优反馈控制的显式表达及最优性能指标值.值得提出的是，本文一方面推广了文献[6]的相关结果，另一方面也通过几个注解指出了文献[15]研究中有待改善的地方并给出了解释.在接下来的研究中，希望能够利用本文得到的相关结果研究广义主-从随机LQ微分博弈问题，这也将充实随机微分博弈的相关研究.

参考文献：

[1] LEWIS F L. A survey of linear singular systems[J]. Circuits, Systems and Signal Processing, 1986, 5(1): 3-36.

[2] DAI L. Singular Control Systems[M]. New York: Springer-Verlag, 1989.

[3] HAIDAR A, BOUKAS E K. Exponential stability of singular systems with multiple time-varying delays[J]. Automatica, 2009, 45(2): 539-545.

[4] XU S, LAM J, ZOU Y, et al. Robust admissibility of time-varying singular systems with commensurate time delays[J]. Automatica, 2009, 45(11): 2714-2717.

[5] YONG J, ZHOU X Y. Stochastic Controls: Hamiltonian Systems and HJB Equations[M]. New York: Springer, 1999.

[6] CHEN S, ZHOU X Y. Stochastic linear quadratic regulators with indefinite control weight costs. II[J]. SIAM Journal on Control and Optimization, 2000, 39(4): 1065-1081.

[7] AIT RAMI M, ZHOU X Y. Linear matrix inequalities, Riccati equations, and indefinite stochastic linear quadratic controls[J]. IEEE Transactions on Automatic Control, 2000, 45(6): 1131-1143.

[8] ZHOU X Y, LI D. Continuous-time mean-variance portfolio selection: A stochastic LQ framework[J]. Applied Mathematics & Optimization, 2000, 42(1): 19-33.

[9] LI X, ZHOU X Y. Indefinite stochastic LQ controls with Markovian jumps in a finite time horizon[J]. Communications in Information and Systems, 2002, 2(3): 265-282.

[10] ZHANG W, CHEN B S, TANG H, et al. Some remarks on general nonlinear stochastic H∞control with state, control, and disturbance-dependent noise[J]. IEEE Transactions on Automatic Control, 2014, 59(1): 237-242.

[11] BOUKAS E K. Stabilization of stochastic singular nonlinear hybrid systems[J]. Nonlinear Analysis: Theory, Methods & Applications, 2006, 64(2): 217-228.

[12] XIA Y, BOUKAS E K, SHI P, et al. Stability and stabilization of continuous-time singular hybrid systems[J]. Automatica, 2009, 45(6): 1504-1509.

[13] HUANG L, MAO X. Stability of singular stochastic systems with Markovian switching[J]. IEEE Transactions on Automatic Control, 2011, 56(2): 424-429.

[14] ZHANG W, ZHAO Y, SHENG L. Some remarks on stability of stochastic singular systems with state-dependent noise[J]. Automatica, 2015, 51(1): 273-277.

[15] ZHANG Q, XING S. Stability analysis and optimal control of stochastic singular systems[J]. Optimization Letters, 2014, 8(6): 1905-1920.

[16] YONG J. A leader-follower stochastic linear quadratic differential game[J]. SIAM Journal on Control and Optimization, 2002, 41(4): 1015-1041.

[17] BENSOUSSAN A, CHEN S, SETHI S P. The maximum principle for global solutions of stochastic stackelberg differential games[J]. Ssrn Electronic Journal, 2012,53(4). DOI: 10.2139/ssrn.2413990.

[18] ØKSENDAL B. Stochastic differential equations: an introduction with applications[M]. 5th ed. New York: Springer-verlag, 1998.

[19] XU S, VAN DOOREN P, STEFAN R, et al. Robust stability and stabilization for singular systems with state delay and parameter uncertainty[J]. IEEE Transactions on Automatic Control, 2002, 47(7): 1122-1128.

Linear Quadratic Control of Continuous-time Singular Stochastic Affine Systems

Zhu Huai-nian1, Zhang Cheng-ke1, Cao Ming2, Bin Ning2

(1.School of Economics & Commence; 2.School of Management, Guangdong University of Technology, Guangzhou 510520, China)

Abstract:Linear quadratic control of a class of continuous-time singular stochastic affine systems is investigated. After establishing some concepts of the stability for stochastic singular systems, the condition of the stability is presented by means of a linear matrix inequality. Then, by utilizing Riccati equation approach, the existent conditions of optimal feedback control in finite horizon and infinite horizon are respectively obtained by means of a generalized differential Riccati equation or a generalized algebraic Riccati equation. And explicit expressions of the optimal feedback controls and optimal cost function are given.

Key words:singular stochastic affine systems; linear quadratic control; linear matrix inequality; Riccati equation

收稿日期:2015-09-17

基金项目:国家自然科学基金资助项目(71771061， 11501129， 71571053);广东省自然科学基金资助项目(2015A030310218, 2014A030310366)

作者简介:朱怀念(1985-)，男，讲师，博士，主要研究方向为动态博弈理论及其应用.

doi:10.3969/j.issn.1007-7162.2016.02.005

中图分类号:F224.32

文献标志码:A

文章编号:1007-7162(2016)02-0024-07