基于数学模型的太阳影子定位问题研究

周　千，李文胜

(西安航空学院 理学院，陕西 西安 710077)

基于数学模型的太阳影子定位问题研究

周千，李文胜

(西安航空学院 理学院，陕西 西安 710077)

摘要：针对太阳影子的定位问题，通过分析影响影子长度的各个参数，建立了影子变化的数学模型。同时，根据某固定直杆在水平地面上的太阳影子顶点坐标数据，通过建立数学模型确定了直杆所处的地点以及视频拍摄的时间。该模型在实际生活中有着极为广泛的应用，具有一定的实际意义。

关键词：太阳影子定位；数学模型；太阳高度角

0引言

随着数字视频在生活中的广泛应用，对于所拍摄的视频，在特殊情况下，需要确定视频的拍摄地点和拍摄日期，太阳影子定位技术[1-2]就是通过分析视频中物体的太阳影子变化，确定视频拍摄的地点和日期的一种方法。本问题源自于2015年全国大学生数学建模竞赛A题。原问题要求建立影子变化的数学模型，并分析影子长度关于各个参数的变化规律，同时，根据某固定直杆在水平地面上的太阳影子顶点坐标数据，通过建立数学模型确定直杆所处的地点以及视频拍摄的时间。本文探讨了相关的问题，并给出了相应的数学模型。

1影子变化模型的建立与求解

假设地球为球体，建立空间直角坐标系如图1所示。以地球球心为坐标原点，z轴正方向指向N极，xOy坐标平面与赤道面重合，则可得球面方程：

x2+y2+z2=α2

将球面方程转化为曲面的参数方程：

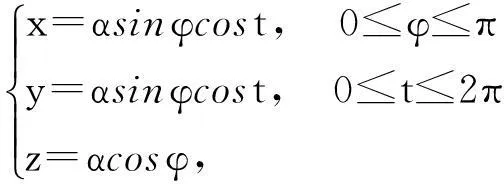
(1)

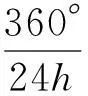
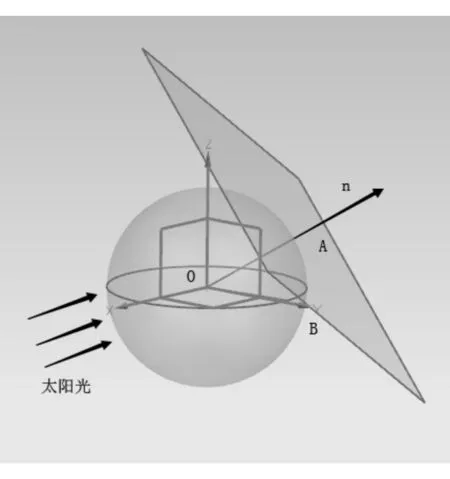
图1　纬度和时角示意图

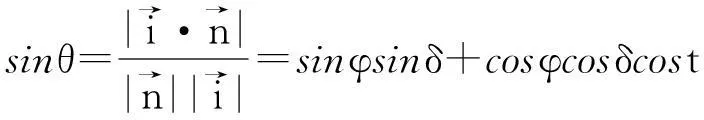
(2)

太阳赤纬δ，即太阳直射点的纬度，计算公式[3]：

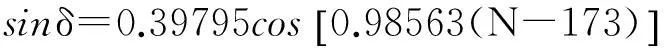
(3)

由于中国采取的是北京时区的区时作为所在的东八区时间，但北京时间并不是北京(东经116.4°)地方的时间，而是东经120°地方(约为陕西蒲城)的地方时间。故

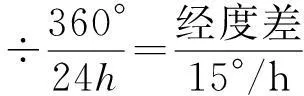
(4)

所求地方时=已知地的地方时±地方时差

(5)

根据直杆与影长的几何关系，由三角函数公式可得；

L=Hcoth

(6)

结合公式(2)(6)化简可得：

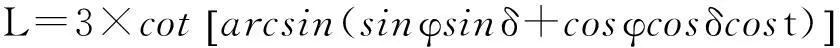
(7)

下面分析影子长度L与各参数(φ，δ)之间的变化关系：

(1)当δ=23°26′N,t=0°时，可以得到北半球夏至日影长L随纬度φ的变化规律，如图2所示：

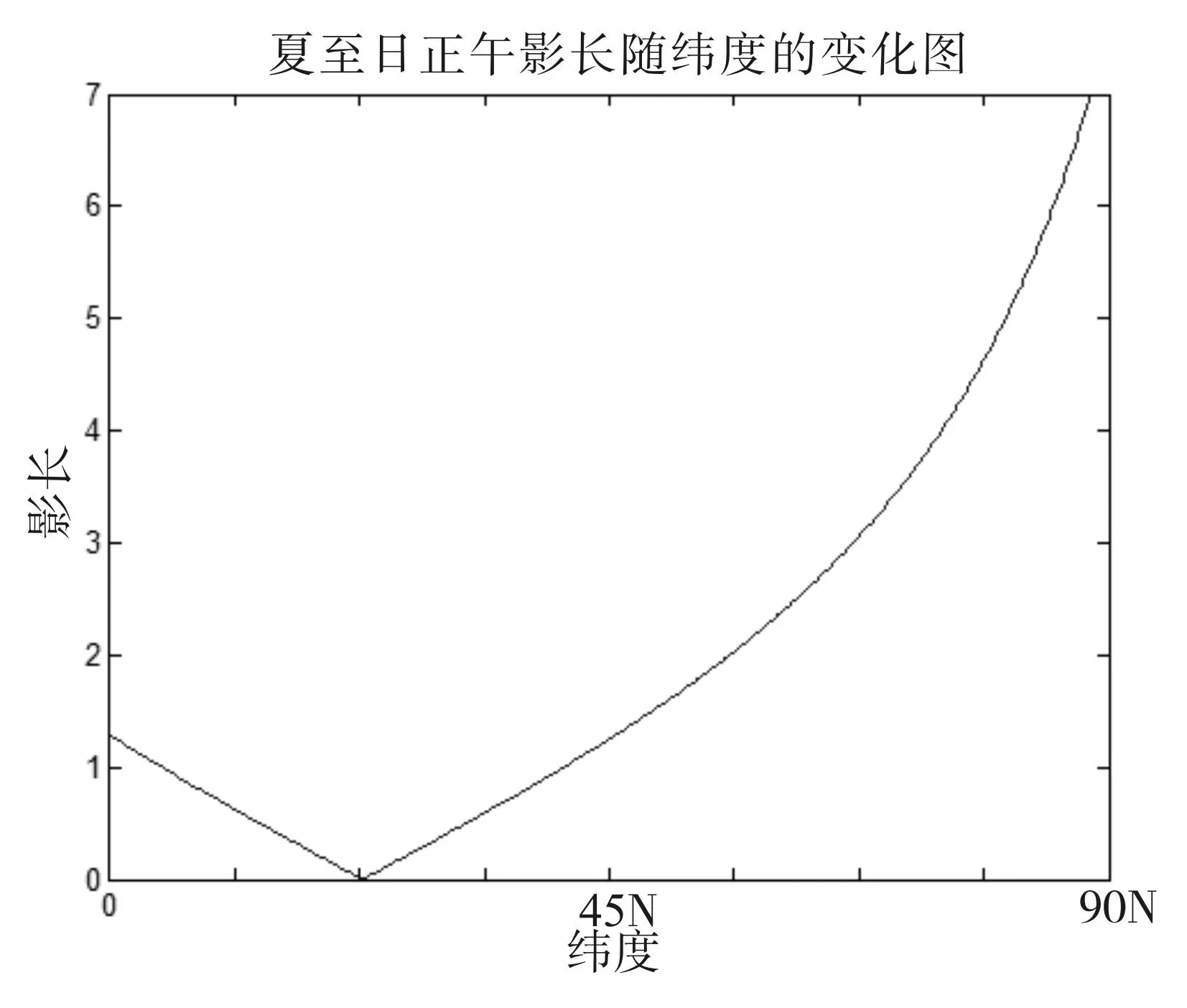
图2　影长随纬度变化图

由图可以看出，夏至日影长从赤道到太阳直射点(北回归线)逐渐变短，从太阳直射点到北极影长逐渐变长。

(2)当φ=39°54′26″N,t=0°时，可以得出影子长度L随太阳直射点纬度(赤纬)δ的变化规律，如图3所示：

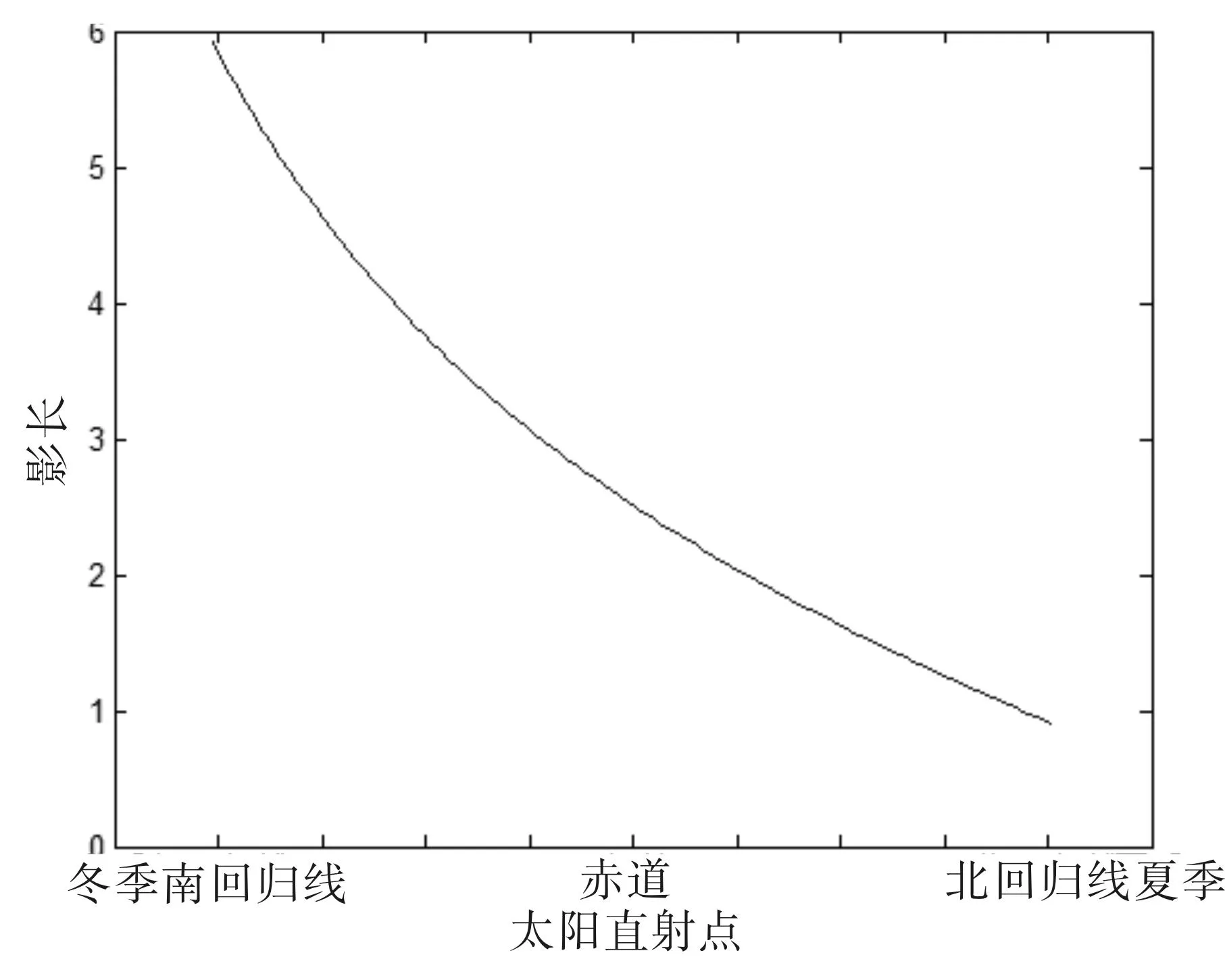
图3　影长随太阳直射点纬度的变化图

由图可以看出，当太阳直射点由南回归线(冬季)到达北回归线(夏季)时，正午的影长由长变短。

2直杆所在地点、日期的模型建立与求解

以直杆底端为原点，水平地面为xOy平面，建立直角坐标系，但是由于实际问题中通常并未给定x轴，y轴的正方向，在夏季正午时，影子的方向为正北方向，故不妨定义一个Y轴偏角[4]的概念。Y轴偏角是指直角坐标系y轴与正南方向的夹角。如图4所示：

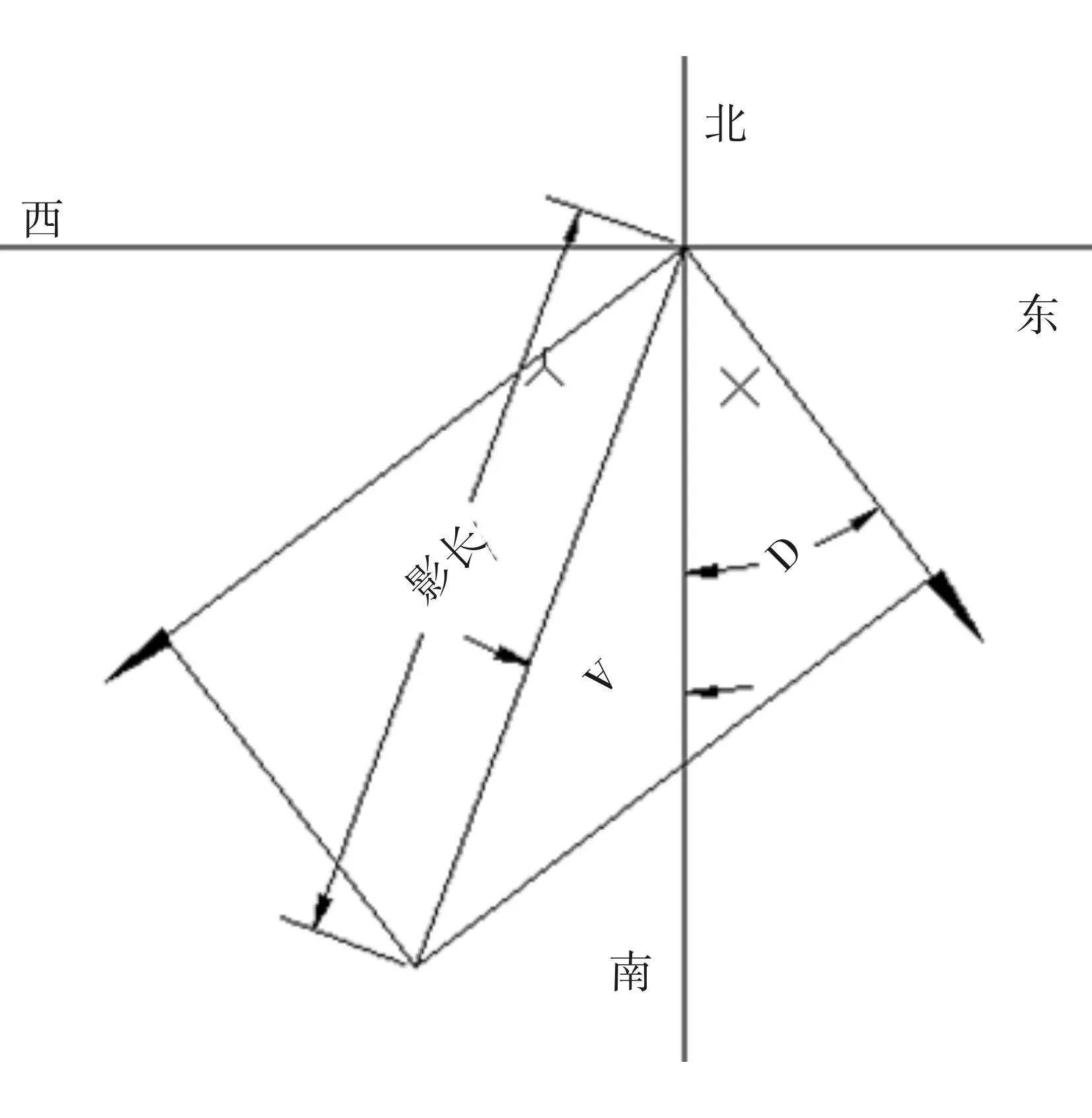
图4　Y轴偏角示意图

为计算Y轴偏角α的大小，利用坐标点进行多项式拟合，发现二次曲线拟合的修正决定系数(Adjusted R-square)已经达到1，所以采用二次拟合，做出影子的轨迹如图5所示：

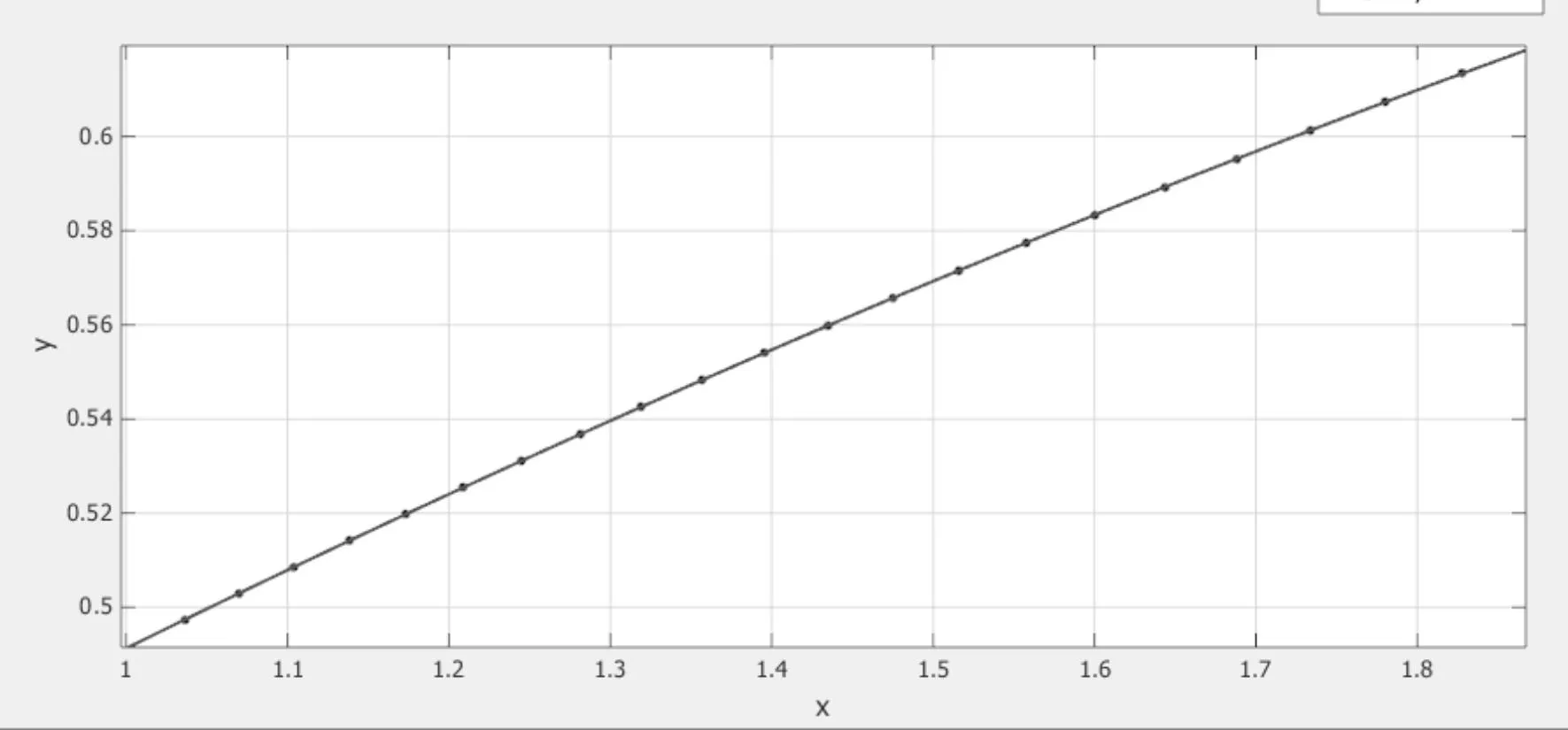
图5　影子的拟合轨迹

影子轨迹拟合方程：

y=-0.02583x2+0.2206x+0.2965

为寻找最短影长的轨迹坐标点，用曲线到原点的距离公式：

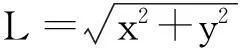
对上式求一阶导数，求出L极小值所对应的坐标点：(x0,y0)=(-0.0632,0.2825)

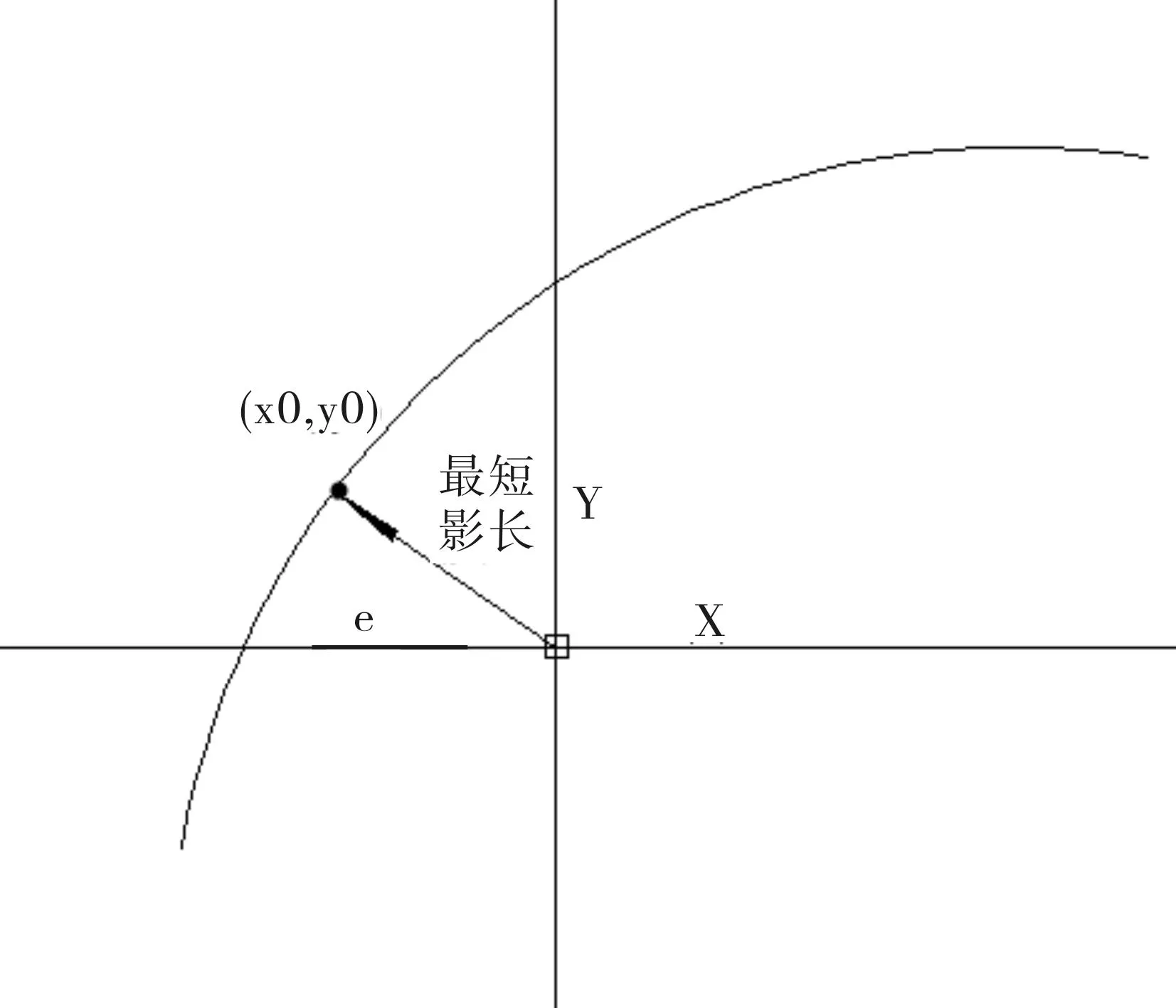
图6　影子向量示意图

可由公式：

求得：α=12.6306°

引入太阳方位角的概念[5]。太阳方位角是指太阳光线在地平面上的投影与当地经线的夹角，可近似地看作是竖立在地面上的直线在阳光下的阴影与正南方的夹角。

因此，可得出影子轨迹的参数方程：

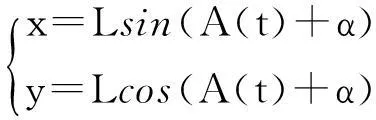
(8)

由(8)式可推导出公式：

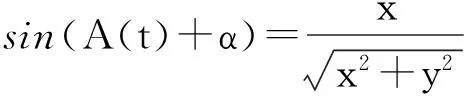
(9)

建立地平面坐标系，通过太阳高度角θ和太阳方位角A来确定太阳位置。如图7所示：

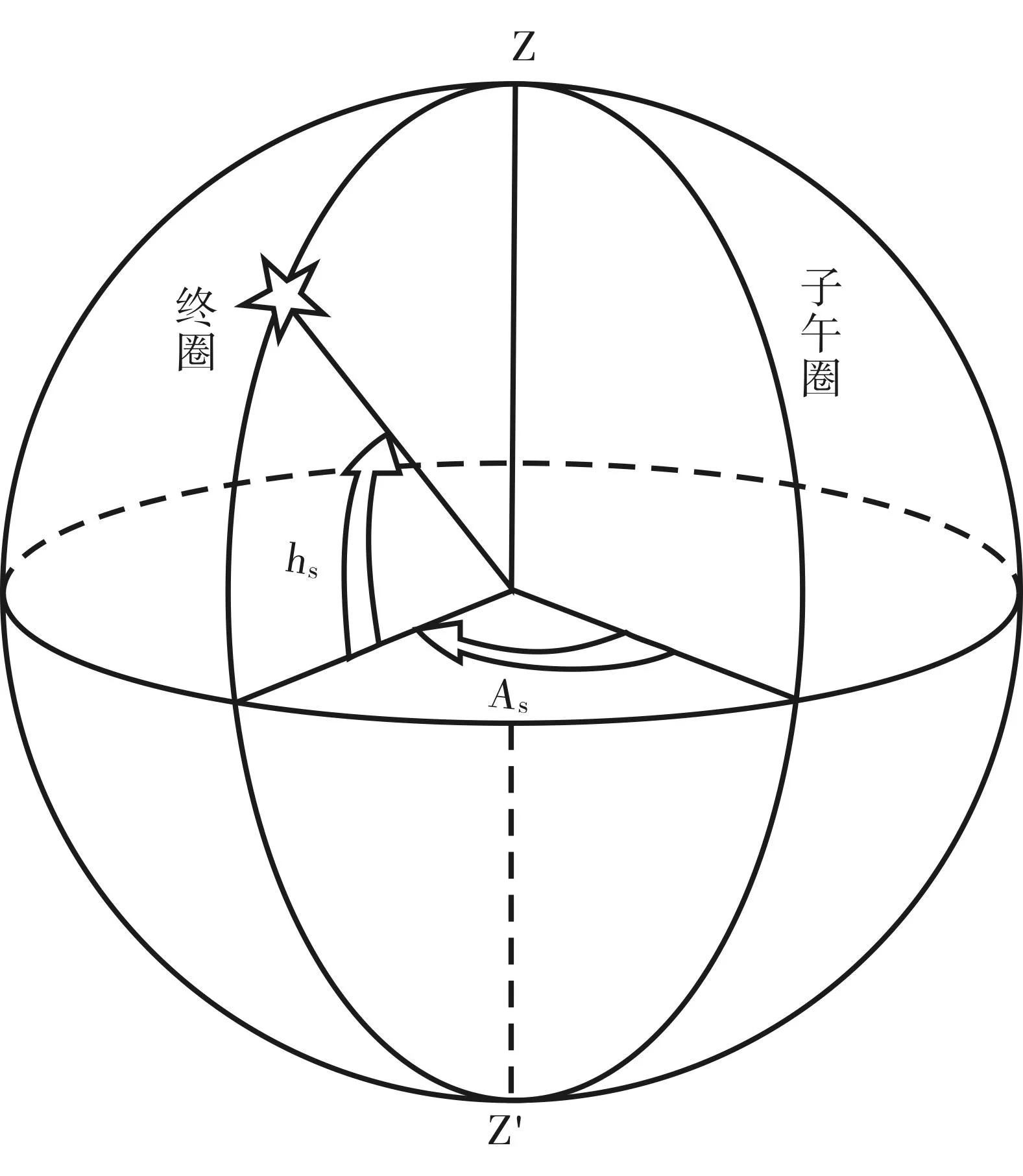
图7　太阳高度角示意图

太阳方位角A方程如下：

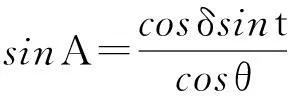
(10)

由(10)式通过三角变换可以得到：

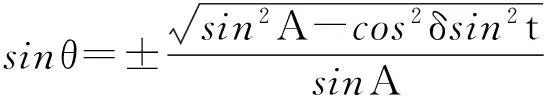
(11)

由(2)(11)可以得到：

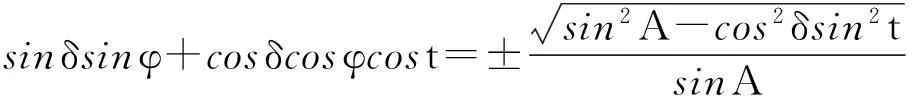
(12)

化简可得：

(13)

3模型的评价与推广

文中讨论了影子长度关于各个参数的变化规律，并通过建立数学模型[6]确定了直杆所处的地点以及视频拍摄的时间。

同时，引入了Y轴偏向角的概念，更加接近于实际问题。文中给出的确定直杆所处地点及拍摄时间的方法，可以推广至有关部门确定图片或视频的拍摄时间或地点问题。模型仍然存在一些不足之处，由于忽略了泰勒展开式中三次以上的项，采用二次曲线拟合影子变化规律，与实际方程存在一定误差。

参考文献

[1] 陈晓勇，郑科科.对建筑日照计算中太阳赤纬角公式的探讨[J].浙江建筑，2011,28(9):6-8,12.

[2] 屈名,王征兵,王德麾.基于交比不变性的太阳定位算法的研究[J].硅谷,2013(19):53-55.

[3] 李飞,白艳萍.用遗传算法求解旅行商问题[J].中北大学学报(自然科学版),2007,28(1):49-52.

[4] 王小平,张丽杰,常佶.基于单高斯背景模型运动目标检测方法的改进[J].计算机工程与应用,2009,45(21):118-120.

[5] 李保来.基于高精度算法的太阳动态跟踪技术研究[D].合肥：合肥工业大学，2012.

[6] 司守奎.数学建模算法与应用[M].北京：国防工业出版社，2011.

[责任编辑、校对：梁春燕]

Research into the Sun Shadow Location Based on Mathematical Model

ZHOUQian,LIWen-sheng

(School of Science,Xi′an Aeronautical University,Xi′an 710077,China)

Abstract：Facing the problem of sun shadow location,the mathematical model of shadow change is established by analyzing the parameters affecting the length of the shadow.At the same time,according to the data of the solar shadow vertex coordinates of a fixed straight bar on the horizontal ground,the mathematical model is established to determine the location and the time of video shot.The model has wide applications in practical life,so it has a certain practical significance.

Key words：sun shadow location;mathematical model;solar elevation angle

收稿日期：2016-04-20

基金项目：陕西省教育厅专项科研计划项目(15JK1379)；西安航空学院科研基金资助项目(2016KY1214，2014KY1210)

作者简介：周千(1981-)，男，山西大同人，讲师，从事基于偏微分方程的图像处理研究。

中图分类号：O242

文献标识码：A

文章编号：1008-9233(2016)03-0076-04