基于动态面控制的多弹协同制导控制方法

王晓芳, 刘冬责, 郑艺裕

(1.北京理工大学 宇航学院, 北京 100081;2.哈尔滨工业大学 深空探测基础研究中心, 黑龙江 哈尔滨 150001)

基于动态面控制的多弹协同制导控制方法

王晓芳1, 刘冬责1, 郑艺裕2

(1.北京理工大学 宇航学院, 北京 100081;2.哈尔滨工业大学 深空探测基础研究中心, 黑龙江 哈尔滨 150001)

摘要:为实现多枚导弹对目标进行饱和攻击,基于动态面控制理论设计了具有攻击时间约束的制导控制方法。综合弹目距离方程和动力学方程建立了制导控制一体化模型,改进设计了基于弹目距离信息的协同策略;考虑导弹速度变化、目标运动、导弹框架角受限以及避免控制器奇异等因素,设计了协同策略中的关键参数,并给出了导弹群理想协同攻击时间的选取方法。在导弹控制输入受限的前提下,采用动态面控制理论设计了导弹扰动鲁棒控制器。仿真结果表明,所提方法能够在满足多种约束的前提下,以较高的精度实现对目标的饱和攻击。

关键词:饱和攻击; 制导控制一体化; 动态面控制

0引言

多枚导弹对目标进行协同饱和攻击是提高导弹的战场生存能力及打击能力的重要手段,已受到越来越多的关注。因此,在考虑战场实际情况的前提下,研究能使多枚导弹同时到达目标、具有攻击时间约束的协同制导方法具有重要意义。

针对具有攻击时间约束的协同制导方法,国内外学者进行了一些研究[1-3];但研究中一般假设导弹的速度为常值,而且用到了预估的导弹剩余飞行时间,而对导弹剩余飞行时间的准确预估一直是个难点[4-5]。文献[6]将对攻击时间的控制问题转化为对弹目距离的跟踪问题,避免了对导弹剩余飞行时间的估计,但该方法中并未考虑鲁棒性问题。在实际作战环境下,导弹会受到风等各种干扰,其气动参数会产生摄动,另外,导弹的速度通常也是变化的,导弹的控制输入是有限的,因此,研究更符合实际情况、更容易实现、具有鲁棒性的攻击时间协同制导方法具有重要意义。

传统的制导方法设计并不考虑导弹的动力学特性。近年来,将导弹的动力学特性简化为滞后环节的最优制导律研究得到发展[7-8],但上述滞后环节并不能真正反映导弹的动力学特性,上述制导律也未涉及对攻击时间的约束。

本文在考虑导弹建模误差以及受到的干扰等不确定性因素的基础上,基于弹目距离变化方程和导弹动力学方程建立了制导控制一体化数学模型。借鉴文献[6],设计了避免剩余飞行时间估计问题的协同策略,并对协同策略中关键参数的设计方法进行了详细分析。基于动态面控制理论设计了具有鲁棒性的制导控制一体化控制器,并严格证明了其稳定性。仿真结果验证了所设计的协同策略和控制器能够有效地控制多枚导弹对目标实施饱和攻击。

1制导控制一体化控制模型

1.1导弹-目标相对运动模型

导弹与目标间的相对运动方程为[9]:

(1)

式中:下标m,t分别代表导弹和目标;r为弹目距离;λ为视线角;ηm和ηt分别为导弹和目标的速度前置角;μm和μt分别为导弹和目标的航向倾斜角。

对式(1)中的第一式求导并考虑第二式得:

(2)

式中:am和at分别为导弹和目标的法向加速度。

1.2导弹制导控制一体化模型

纵向平面内,描述导弹非线性动力学特性的方程为[9]:

(3)

考虑升力和俯仰力矩的主要组成部分可得到:

(4)

(5)

式中:Q为动压;S为特征面积;l为特征长度;Ld和Md分别为其他因素产生的升力和俯仰力矩。

忽略推力、重力对导弹航迹倾斜角变化的影响,可得:

(6)

(7)

式中:dμm和da为建模误差。

将式(7)代入式(2)可得:

(8)

对式(3)中的第四式求导,并考虑式(6)可得:

(9)

将式(5)代入式(3)中第三式得:

(10)

考虑导弹舵偏角的幅值是有限的,有:

(11)

式中:δe,max为舵偏角的最大幅值。

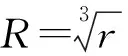
(12)

其中:

sat(δe)为考虑控制输入舵偏角受限的函数:

(13)

式(12)即为考虑控制输入受限的制导控制一体化控制模型。

2协同策略

假设理想的攻击时间为Td,借鉴文献[6]的思路,定义标称弹目距离:

(14)

式中:γ>0为待设计参数。由式(14)可知,当t=Td时,rd=0。如果控制器能够控制每枚导弹的弹目距离良好地跟踪标称弹目距离,则可实现各导弹均在Td时刻命中目标,实现多导弹协同攻击。

3制导控制一体化控制器

3.1基于动态面理论的控制器设计

由式(12)可见,该控制模型是一个具有严格反馈级联形式并带有有界不确定性的系统,可采用动态面控制理论进行鲁棒控制器的设计。

考虑到舵偏角的有限性,构建与式(12)具有相同阶次的辅助系统[10]:

(15)

式中:i=1,2,3;hi>0;h4>0;Δδe=sat(δe)-δe。

接下来,基于动态面控制理论设计控制器。

(1)定义动态面:

(16)

对S1求导,并考虑式(12)的第一式可得:

(17)

令x2为虚拟控制量,考虑辅助系统式(15),设x2的变化规律为:

(18)

式中:k1>0为动态面增益。

为避免对x2c求导,可通过低通滤波器滤波:

(19)

式中:τ2为滤波器时间常数;x2d为x2的期望值。

(2)定义动态面:

(20)

参考步骤(1)的方法,设计

(21)

并令x3c通过低通滤波器进行滤波。

(3)动态面S3的定义与设计同S2。

(4)定义动态面:

(22)

按照前述方法设计舵偏角表达式如下:

(23)

由设计过程可见,基于此控制器,可根据制导指令直接求得导弹的控制输入——舵偏角信号,体现了制导控制一体化的设计思路。

3.2稳定性分析

定义边界层误差:

(24)

对式(24)求导,并考虑式(19)可得:

(25)

根据控制器的推导过程可得到:

(26)

(27)

(28)

(29)

定义李雅普诺夫函数：

(30)

对式(30)两端求导,并将式(25)～式(29)代入,由不等式原理得:

(31)

令:

式中:χ>0。则有:

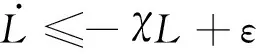
(32)

根据比较原理,由式(32)可得:

(33)

如果在导弹整个飞行过程中,舵偏角始终处于饱和状态,则导弹无法命中目标;故假设在t→∞时Δδe=0°，此时ε为常值。由式(33)可知,Si和yi最终一致有界,式(12)所示系统的状态变量xi也最终一致有界。

3.3协同策略关键参数设计

由于g1=-CLαQSsinηm/(3r2/3m),因此当速度前置角ηm=0时,g1=0。由式(21)可知,此时x3c→∞,算法出现奇异。可通过设置协同策略中的参数γ、初始时实际弹目距离r0和标称弹目距离rd0来避免奇异的发生。

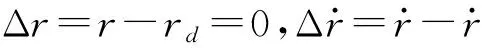
(34)

此时可求得r跟踪上rd后导弹的速度前置角:

(35)

通常,用于协同攻击目标的导弹的速度都是非减的,由此可知导弹的初速Vm0为导弹的最小速度。另外,假设目标作匀速直线运动,并记p=Vt/Vm0为最大的目标与导弹速度比,p通常比较小。此时有:

(36)

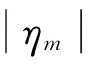
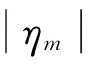
在已知导弹的初始弹目距离r0及已设定的Δr0的基础上,可计算出初始的标称弹目距离rd0=r0-Δr0,从而根据式(14)计算出:

(37)

Td0即可作为理想攻击时间Td。对于多枚导弹协同作战的情况,可取所有导弹理想攻击时间中最大者作为导弹群理想的协同攻击时间Td,即

(38)

式中:n为导弹编号;N为参与协同攻击的总导弹数。

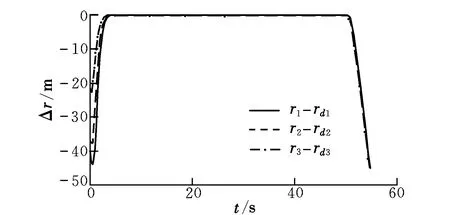
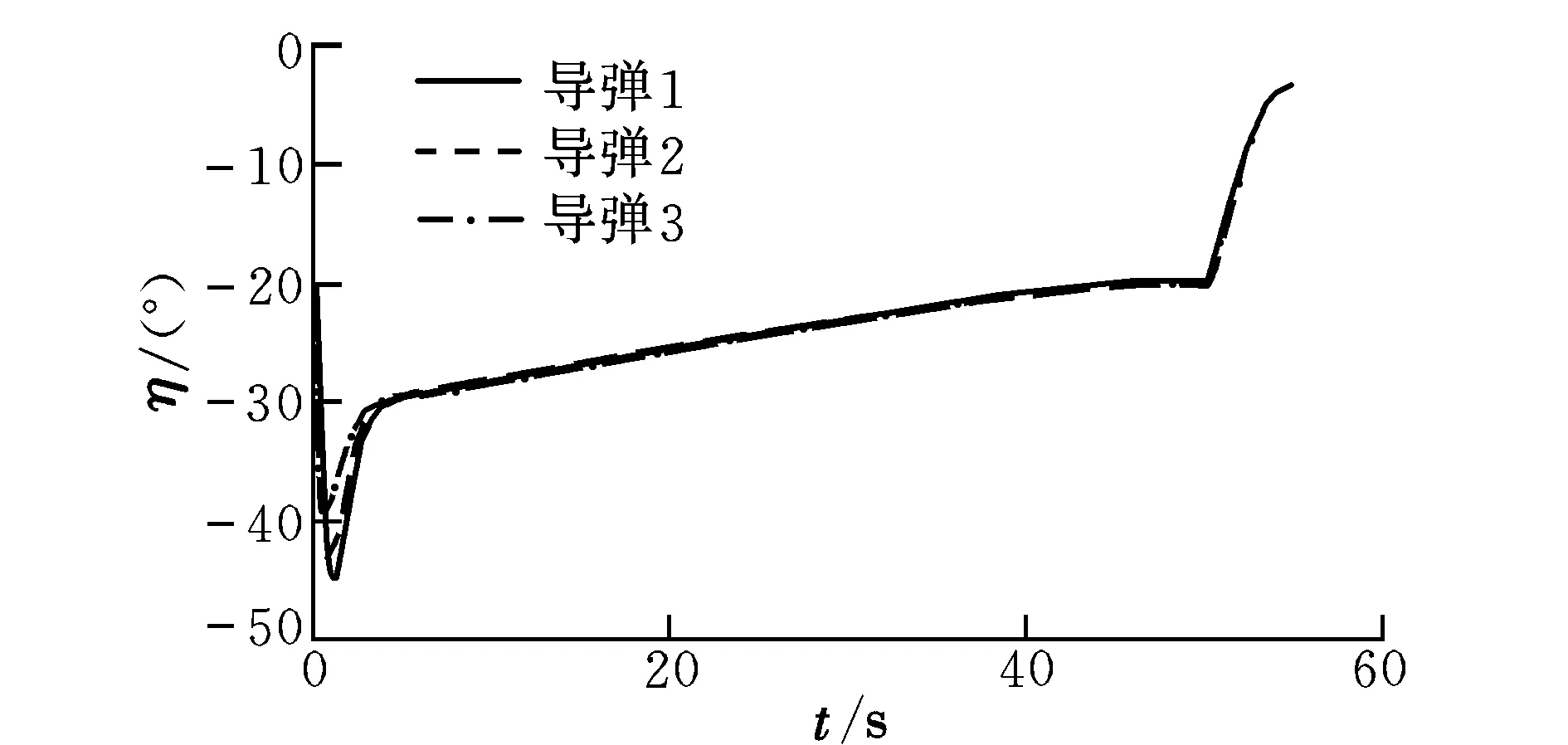
当r

4仿真验证及结果分析

假设三枚反舰导弹协同攻击舰艇,舰艇的初始位置为xt=0,yt=0,速度为Vt=15 m/s,航向角为μt=0。用来协同作战的三枚导弹属于同类型导弹。三枚导弹的发射参数如表1所示。

表1　导弹的发射参数

假设三枚导弹的速度变化规律为0.5 m/s2,在飞行过程中,导弹1、导弹2和导弹3的气动参数分别摄动20%,25%和30%。最大舵偏角δe,max=10°。

假设ηm,min=10°,可得γ=0.91。取三枚导弹的初始Δr0=-20 m,则根据式(38)可得到Td1=55.06 s,Td2=55.08 s,Td3=55.15 s,因此取导弹群的理想协同攻击时间Td=Td3=55.15 s。根据稳定性条件,控制器参数取ki=6 (i=1，…，4),低通滤波器时间常数τi=0.01 (i=2,3,4),辅助系统中的hi=3 (i=1，…，4),转比距离r*=1 000 m。仿真结果如图1～图4所示。

图1　导弹弹道与目标运动轨迹Fig.1　Trajectory of missiles and target

图2　实际弹目距离与标称弹目距离差Fig.2　Difference between the r and rd

由仿真数据可知,三枚导弹命中目标的时间分别为54.91 s,54.905 s和54.895 s,几乎同时命中目标,实现了对目标的有效饱和协同攻击。由图2可见,在控制器的作用下,三枚导弹的实际弹目距离与标称弹目距离之差很快变为0,实现了r对rd的良好跟踪。飞行末段的弹目距离差是由于协同制导控制律转为比例导引律的缘故。

图3　速度前置角变化曲线Fig.3　Variation of velocity heading angle

图4　舵偏角变化曲线Fig.4　Variation of deflection angle of rudder

5结束语

针对多枚导弹对目标进行协同饱和攻击的情况,综合考虑导弹的制导与控制问题,提出一种适用于变速导弹攻击运动目标的鲁棒协同制导控制方法。本方法考虑了导弹的建模误差和所受到的干扰、舵面偏转的有限性、避免碰框等问题,另外,所用的制导信息便于测量;因此,其更接近于工程应用,具有广阔的军事应用前景。

参考文献：

[1]Jeon I S,Lee J I,Tahk M J.Impact-time-control guidance law for anti-ship missiles[J].IEEE Trans.on Control Systems Technology,2006,14(2):260-266.

[2]张功,李帆,赵建辉,等.弹着时间可控的机动目标多弹协同制导律[J].指挥控制与仿真,2010,32(1):52-55.

[3]Jeon I S,Lee J I,Tahk M J.Homing guidance law for cooperative attack of multiple missiles[J].Journal of Guidance,Control,and Dynamics,2010,33(1):275-280.

[4]Tahk M J,Ryoo C K,Cho H.Recursive time-to-go estimation for homing guidance missiles[J].IEEE Trans.on Aerospace and Electronic Systems,2002,38(1):13-24.

[5]Lin L,Kirubarajan T,Bar-Shalom Y.Pursuer identification and time-to-go estimation using passive measurements from an evader[J].IEEE Trans.on Aerospace and Electronic Systems,2005,41(1):190-204.

[6]张友安,张友根,彭军. 一种导弹攻击时间协同导引律[J].海军航空工程学院学报,2009,24(1):34-38.

[7]Ryoo C K,Cho H,Tahk M J.Optimal guidance laws with terminal impact angle constraint[J].Journal of Guidance,Control,and Dynamics,2005,28(4):724-732.

[8]陈欢,刘蛟龙,尉建利,等.考虑高阶系统动力学滞后的最优制导律研究[J].飞行力学,2014,32(1):38-47.

[9]钱杏芳,林瑞雄,赵亚男.导弹飞行力学[M].北京:北京理工大学出版社,2013:49-93.

[10]郑艺裕.导弹协同作战制导与控制方法研究[D].北京:北京理工大学,2014.

(编辑：李怡)

Cooperative guidance and control law for multiple missiles based on dynamic surface control

WANG Xiao-fang1, LIU Dong-ze1, ZHENG Yi-yu2

(1.School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China;2.Deep Space Exploration Research Center, Harbin Institute of Technology, Harbin 150001, China)

Abstract:To realize cooperative saturation attack of multiple missiles, a guidance and control law with impact time constraint was designed based on dynamic surface control. The equation expressing the change of missile’s range-to-go and the dynamic equation of missile were synthesized to make up the integrated guidance and control model. A cooperative strategy that was about the information of missile’s range-to-go was improved, and the key parameter of the strategy was designed considering missile’s variable velocity, moving target, the limited gimbal angle of missile and voiding the singularity of the controller. Also the setting method of ideal cooperative attacking time of multiple missiles was proposed. Taking the limited control input of missile into account, a robust controller based on dynamic surface control theory was designed. Simulation results show that the proposed method can make multiple missiles realize cooperative saturation attack with high precision while satisfying multiple constraints.

Key words:saturation attack; integrated guidance and control; dynamic surface control

收稿日期:2015-09-11;

修订日期:2015-12-08; 网络出版时间:2016-02-29 16:37

基金项目:国家自然科学基金资助(11502019)

作者简介:王晓芳(1979-)，女，山西晋中人，副教授，博士，主要研究方向为飞行器协同制导与控制、飞行器总体设计； 刘冬责(1990-)，男，黑龙江七台河人，硕士研究生，主要研究方向为飞行器协同制导与控制、飞行力学； 郑艺裕(1988-)，男，福建漳州人，博士研究生，主要研究方向为飞行器轨迹设计、制导与控制。

中图分类号：TJ765.3

文献标识码：A

文章编号：1002-0853(2016)03-0048-05