通过信号处理提高时域EMI的测量准确度

牛宏亮

【摘 要】利用短时FFT算法对时域数据进行频谱分析，信号需满足平稳性假设条件，因此对尖峰、脉冲等瞬态信号无法得到正确的分析结果。重叠FFT是对非平稳信号进行时域分析的有力工具，其引入不同的交叠深度，对采样信息进行精细分析，这样可以避免因为窗函数的两端零点对干扰信号可能造成的频谱泄露，实现对非周期、尖峰、脉冲以及跳频等瞬态信号的无缝捕获。

【关键词】电磁干扰；瞬态信号；重叠傅里叶变换；短时傅里叶变换

【Abstract】Analyse the time-domain data of spectrum with short-time FFT algorithm， the signal need to meet stationarity assumptions. Therefore， transient signal such as peak and impulse， cannot get the correct analysis results.Overlapping FFT is a powerful tool for time domain analysis of non-stationary signal.Bring in different overlapping depth， detailed analysis was carried out on the sample information. So it can avoid leakage frequency spectrum which the zero point of both window function sides may influence on the interference signal.It can seamless capture the transient signal， such as aperiodic， peak， impulse and frequency hopping.

【Key words】Electromagnetic interference； Transient signal； Overlapping FFT； Short-time FFT

0 前言

随着越来越多的电子电器设备在科研生产和日常生活中的广泛应用，电磁干扰（electromagnetic interference，EMI）问题也日益突出。在诸多的电磁干扰现象中，周期性的干扰易于发现，但那些偶发性的电磁干扰现象由于其自身的不规律性，采用传统的EMI接收机去测量往往很难发现，会发生频谱泄露现象，从而使得测量结果失真[1]。

针对上述问题，本文对时域EMI测量技术中的信号处理环节进行了改进，提出一种为新的信号处理方法—重叠FFT算法，来解决瞬态信号难以准确测量的问题。重叠FFT算法主要是根据CISPR16-1-1标准的要求[2]，为了能够捕获并分析瞬态干扰信号，不同于传统的顺序处理采样点的信息，而是引入了不同的交叠深度，对采样信息进行精细分析，这样可以避免因为窗函数的两端零点对干扰信号可能造成的频谱泄露，实现对瞬态干扰信号的测量。

1 短时FFT（Short-Time FFT，STFFT）算法

利用FFT算法可以对宽带时域数据进行频谱分析，但使用FFT时，需要信号满足平稳性假设条件，对尖峰、脉冲等瞬态信号无法得到正确的分析结果[3，4]。STFFT是对非平稳信号进行时域分析的有力工具，它在FFT前乘上一个时间有限的窗函数，将信号划分为多个短时间间隔的块进行并行快速处理，从而得到信号的一组局域频谱，根据不同时刻局部频谱的差异，获得信号的时变特性。在本文中，采用STFFT对时域信号进行处理，实现对非周期、尖峰、脉冲以及跳频等瞬态信号的无缝捕获。

时域EMI测量系统在进行电磁干扰测量时，由于实时数字信号处理单元处理的数据量巨大，每秒钟处理的数据量达到Gbps级别。如此规模的数据吞吐量一般由超大规模FPGA阵列组成的硬件模块来作为基础平台来应对，因此高效的数据处理算法就显得尤为必要。为了完成数据处理的繁重任务，可采用短时FFT信号处理算法。把数据分流到FPGA阵列中，然后采用短时FFT信号处理算法，在每一个FPGA芯片上，把数据分割成大量的短时间间隔块，由FPGA芯片内部丰富的内嵌功能单元来完成短时数据块的处理。

2 重叠FFT（Overlapping FFT）算法

为了实现对非周期、尖峰、脉冲以及跳频等瞬态电磁干扰信号的准确测量，本文设计了一种重叠FFT信号处理技术。

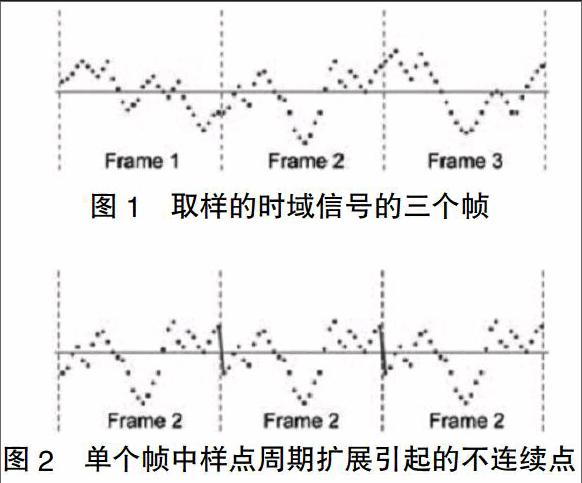
在短时FFT算法分析中，一个固有的假设是要处理的数据是单个周期定期重复的信号。图1描述了一系列时域样点。

假如在帧2上使用 FFT 处理时，在信号上进行周期扩展。一般会在连续帧之间发生不连续点，如图2所示。

这些人为的不连续点生成原始信号中不存在的杂散响应，在附近存在大的信号时，不可能检测到小的信号，这种效应称为频谱泄漏[5]。

应用本文设计的重叠FFT算法，可解决频谱泄露效应，以及完成对瞬态信号的无缝测量。

重叠FFT算法主要是根据CISPR16-1-1标准的要求，为了能够捕获并分析瞬态干扰信号，不同于传统的顺序处理采样点的信息，而是引入了不同的交叠深度，对采样信息进行精细分析，这样可以避免因为窗函数的两端零点对干扰信号可能造成的频谱泄漏，实现对瞬态干扰信号的测量[6]。

重叠FFT算法的一个核心就是把待处理的数据依据一定的长度划分为一个个小的单元，在对这些数据进行时频分析分析时，相邻两个单元之间的数据有一定量的重复，这个重复的部分就命名为重叠帧。重叠帧的一个优势是提高了显示更新速率，这一效应在要求采集时间长的窄跨度中最为明显。如果没有重叠帧，那么直到采集整个新帧时才能更新显示屏幕。在使用重叠帧时，将在以前的帧完成前显示新帧。

另一个优点是在频谱图中实现的无缝频域显示。由于窗口滤波器降低了帧的每端样点对零的影响，如果帧没有重叠，在两个相邻帧接合处发生的频谱事件可能会丢失。但是，重叠帧保证了可以在频谱图上查看所有频谱事件，而不考虑窗口效应。

3 仿真验证

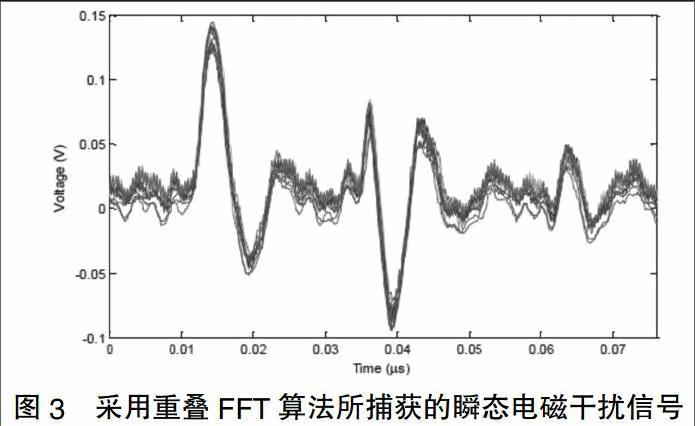
为了评估所设计的测量系统的精确度，采用配置为Intel Celeron 600-MHz的台式电脑对其测量结果进行分析，台式电脑采用300MHz的时钟对内部CPU进行记录。以一个典型的dc/dc转换器的电磁干扰测量为实例，用时域EMI测量系统，结合重叠FFT信号处理算法对其进行测量。

如图3所示，应用了重叠FFT算法的时域EMI测量系统，在不同时间点上成功捕获到了频率分别为296MHz和188MHz的瞬态电磁干扰信号，充分验证了本算法的有效性。

4 结论

本文在短时FFT算法的基础上，设计了一种新的重叠FFT算法，解决了电磁干扰测量中非周期、尖峰、脉冲以及跳频等瞬态电磁干扰信号难以准确捕获并测量的问题。经过试验验证，本方法准确、有效。随着各种电子电器产品的大规模应用，本算法在电磁干扰测量和电磁干扰预防等领域将有着广泛的应用前景。

【参考文献】

[1]S.Braun，T.Donauer and P.Russer.A realtime time-domain EMI measurement system for full--compliance measurements according to CISPR16-1-1[J].Electromagnetic Compatibility，IEEE Transactions，on vol.50，pp.259-267，May 2008.

[2]M.Pous and F.Silva.Prediction of the impact of transient disturbances in real-time digital wireless communication systems[J]. Electromagnetic Compatibility Magzine，IEEE，vol.3，pp.76 -83，2014.

[3]周先春，石兰芳.数字信号处理[M]，清华大学出版社，2015.

[4]S.Braun.A novel time-domain EMI measurement system for measurement and evalution of discontinuous disturbance according to CISPR 14 and CISPR 16 in electromagnetic compati- -bility[J].IEEE International Symposium on 2011.

[5]G.Costa，M.Pous，A.Atienza and F.Silva.Time-domain Electromagnetic Interference Measure--ment System for intermitent disturbances[J].Electromagnetic Compatibility（EMC Europe）， International Symposium on Gothenburg，2014.

[6]马明，沈越泓，牛英涛，孔昭煜.基于空间时频分布的非平稳信号盲分离算法性能研究[J].测控与控制学报，2007，6（29）：55-61.

[责任编辑：王伟平]