引入最优自适应因子的状态模型法航空重力测量
闫文林, 李英成, 薛艳丽
1 中测新图(北京)遥感技术有限责任公司, 北京 100039 2 山东大学空间科学研究院, 山东威海 264209 3 中国测绘科学研究院, 北京 100830
引入最优自适应因子的状态模型法航空重力测量
闫文林1,2, 李英成1,3, 薛艳丽1,3
1 中测新图(北京)遥感技术有限责任公司, 北京100039 2 山东大学空间科学研究院, 山东威海264209 3 中国测绘科学研究院, 北京100830
摘要引入最优自适应比例因子以改善状态模型法航空重力测量的精度,并尝试将其应用到我国困难地区的重力测量.把重力扰动当作状态量引入Kalman滤波进行最优估计,并引入最优自适应因子调节状态信息的权阵,提高重力扰动的最终解算精度.利用新疆地区不同航次和航高的实测数据,计算了垂直向下方向上的重力扰动.与全球重力场模型EGM2008的对比分析表明,差值中误差在10 mGal左右,接近国家在困难地区重力测量精度的限差要求.关键词航空重力测量; 状态模型法; Kalman滤波; 自适应因子
1引言
我国重力空白区域在我国国土面积中占有很大比重,并且多集中在难以到达的沙漠、水域、高山等区域(陈俊勇等,2001;周坚鑫等,2003;张昌达,2005).传统的静态重力测量手段难以在这些困难区域展开,卫星重力测量由于分辨率较低,也难以满足需求.而航空重力测量以其高精度、高分辨率、高机动性等特点,成为该类地区获取重力信息的有效手段.航空重力测量的研究始于20世纪50—60年代,在80年代末90年代初逐渐成熟.研究表明航空重力测量的精度为2~10 mGal(分辨率6~10 km)(Brozena et al.,1989;Klingelé et al.,1995;Brozena and Childers,2000;Forsberg et al.,2001; Verdun et al.,2002;Rene et al.,2007;孙中苗等,2013a).商用航空重力仪(例如LaCoste & Romberg、BGM、KSS等产品)具有较高的精度和较好的稳定性,但我国对该类设备的引进存在诸多限制.我国在航空重力测量的研究起步较晚,西安测绘研究所和航天科技集团16所率先研制的航空重力测量系统CHAGS,测量精度达到了2~5 mGal(分辨率10 km)(夏哲仁,2004;孙中苗,2004;孙中苗等,2004a,2004b;孙中苗等,2013a).
基于GNSS/INS的航空重力测量是目前研究最为广泛的航空重力测量技术,根据测量原理的不同,可以分为直接求差法和状态模型法(Jekeli,2001).直接求差法由加拿大Calgary大学的Bruton在2000年提出(Bruton,2000),随后Serpas、Senobar等对该方法进行了深入的研究(Serpas and Jekeli,2005;Senobari,2010).在国内,孙中苗等利用直接求差法对CHAGS系统开展了多项研究(孙中苗,2004;孙中苗等,2013b).尽管直接求差法在航空重力测量领域中有较为深入的研究,但该方法对惯性系统的校准精度和系统姿态的测量精度都有严格的要求.与直接求差法不同,状态模型法把重力扰动当作Kalman滤波系统的状态量进行最优估计,在一定程度上降低了对惯性系统的要求.Tomé、Deurloo等的研究成果表明,利用中低精度的惯性系统,根据状态模型法同样可以得到较高精度的重力扰动结果(Tomé,2002;Deurloo et al.,2011;Bastos et al.,2013).目前国内的研究多集中在直接求差法,对状态模型法的研究较少.
自适应Kalman滤波以其调节状态信息的权阵来控制状态误差对参数估计的影响的特性,在定位与导航有着广泛的研究与应用(Yang et al.,2001,2006a, 2006b;Hajiyev and Soken,2013).研究表明引入自适应因子,并根据一些理论或者经验的准则对自适应因子进行合理的估计以后,组合导航系统的性能明显优于经典Kalman滤波(高广为等,2006;Yang et al.,2006a).
本文首先展开对状态模型法航空重力理论研究,给出该方法详细的实现过程,并在状态模型法的基础上引入最优自适应因子算法,调节动力学模型信息和观测信息对滤波结果的影响,改善重力扰动的计算结果,并以新疆地区的实测数据验证该方法的有效性.
2基本原理
根据牛顿第二定律,在惯性坐标系中质点的动力学方程为
(1)
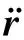
在SINS/GNSS组合导航过程中,在导航坐标系n下,速度测量值对时间求偏导可以得到(TittertonandWeston, 2004):
(2)

(3)
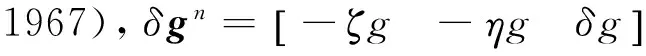
2.1直接求差法航空重力测量
直接求差法主要是通过公式将重力扰动矢量表示为
(4)

(5)
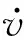
利用公式(2)计算的空中重力扰动含有大量的噪声,而重力扰动信号能量通常集中在低频段很窄的部分.因此需要设计合适的低通滤波器对空中重力扰动进行噪声消除.在航空重力测量领域中,比较典型的低通滤波器有RC低通滤波器、Butterworth低通滤波器、FIR低通滤波器.FIR低通滤波器的差分方程形式可以表示为(孙中苗,2004;孙中苗等,2004b)

(6)
其中x(n)为输入信号,y(n)为输出信号,h(k)为滤波器系数(单位冲激响应),N为滤波器长度.h(k)的理想频率响应可以表示为
(7)
确定单位冲激响应函数主要有切比学夫等纹逼近法和窗函数法,主要做法请参考文献(孙中苗,2004)和(孙中苗等,2004b),本文不再赘述.
2.2引入最优自适应因子的状态模型法航空重力测量
在组合导航领域,位置、速度、姿态、惯性器件的系统误差通常被当作Kalman滤波的系统状态量,通过预计方程和更新方程估计出来.基于状态法的航空重力测量就是通过对重力扰动进行建模,将其作为系统的状态量,利用Kalman滤波进行最优化估计.
以21+1维系统状态的Kalman滤波为例,系统的状态量可以表示为

(8)


(9)




(10)


一个典型的Kalman滤波的预测方程可以表示为
(11)
其中Φk-1近似的公式为

(12)
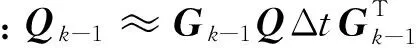
(13)

引入最优自适应因子的更新方程可以表示为
(14)
其中α为最优自适应因子,zk是第k时刻的更新信息,通常是指GNSS的位置和速度的解算结果,Hk为观测矩阵,Kalman增益矩阵Kk为
(15)
其中Rk为更新观测值的协方差矩阵.
tk时刻预测状态向量的协方差可以表示为
(16)
(17)
采用多个历元的平均值并不能有效的反应当前历元的模型误差的大小,因此这里简单的取:
(18)
自适应因子的表达式为(YangandHe,2001;高为广等,2006;Yangetal.,2006a, 2006b;杨元喜,2006)
(19)
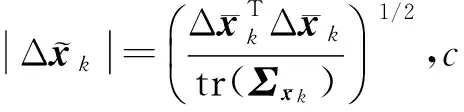
3算例及结果分析
选取西部某地两天航空摄影测量任务的POS(测姿定位系统,PositionandOrientationSystem) 数据进行分析,飞行轨迹分别为图1和图2.搭载的POS系统为IGIAeroControl&AeroOffice,该系统包括一款中等精度的光纤陀螺惯导IMU-d和一款NovAtelOEM4GNSS双频接收机,表1为该系统利用本文的算法计算的位置和姿态结果与航空摄影测量的空中三角测量结果的较差统计表,从表可以看出利用该系统能提供比较可靠的位置和姿态信息.飞行载体的为运八型飞机.在测区内架设有GPS基站,利用GPS差分技术获取高精度的位置、姿态、速度、加速度信息.测试过程中IMU设备的频率为256 Hz,GNSS差分结果的频率为1 Hz.分别利用直接求差法和自适应状态模型法进行航空重力解算.解算结果与全球重力场模型EGM2008在该区域重力扰动资料进行比较,验证结果的精度.EGM2008全球重力场模型是由NGA(National Geospatial-intelligence Agency)发放全球超高阶地球重力场模型,分辨率最高可达2.5′×2.5′(约为5 km格网),研究表明该模型在我国地势平缓的区域的精度能达到10 mGal左右(章传银等,2009;杨金玉等,2012).由于目前掌握该测区的地面重力资料非常有限,本文暂时用EGM2008全球重力模型计算出的重力扰动值作为参考,对初步解算结果进行对比分析.两次测量都在飞机起飞前进行了系统初始对准,系统的初始对准包括POS系统的初始姿态对准和重力扰动的对准,对准时间约为15 min.由于停机坪附近没有重力基准点,系统采用EGM2008模型推算的重力扰动作为初始重力扰动.EGM2008提供的全球重力扰动结果为参考椭球表面的重力扰动,本文利用NGA网站提供的Fortran脚本“EGMhsynth_WGS84.f”和2.5′×2.5′的格网数据进行计算了测试所在区域椭球表面的重力扰动,然后再通过向上延拓公式延拓到航线所在的高度上,将延拓后的结果作为本文计算结果的参考值.测试中采用的向上延拓算法为直接代表法,计算公式为(石磐和王兴涛,1997;孙中苗,2004)

图1 2008年4月14日飞行轨迹Fig.1 Trajectory of flight on 14 April 2008

图2 2008年5月9日飞行轨迹Fig.2 Trajectory of flight on 9 May 2008

差值平均值差值中误差北方向(m)-0.0100.0748东方向(m)-0.0190.1035垂直向下方向(m)0.1060.0294横滚(°)0.03730.0143俯仰(°)0.00660.0045航向(°)0.07650.0070
(20)



(21)
其中
这里的参数φ为纬度,单位为弧度,h为椭球高,单位为m;a,b,e,f是重力模型的椭球参数;参数γp和γe分别为重力模型的极参数和赤道参数;ωe为地球的自转角速度,GM为地球的引力常数.这些地球参数的取值请参照文献 (NIMA, 2000).
3.1算例1
算例1为对新疆某沙漠地带一平均航高6000 m、航迹340 km、航速155 m·s-1的航线进行航空重力解算,飞行轨迹如图3.飞机在飞行过程中受到大气扰动较小,飞行高度稳定在6000 m左右,起伏不超过20 m,航线经过区域为沙漠地带,地面起伏不大.由EGM2008计算该区域的重力扰动分布如图4.

图3 算例1飞行轨迹图Fig.3 Trajectory of flight for case 1
采用直接求差法、状态模型法计算的重力扰动结果与EGM2008模型计算的该航线上的重力扰动如图 5,从图中我们可以看出,利用状态模型法计算出的重力扰动和EGM2008模型的趋势是一致的,自适应状态模型法又较状态模型法的趋势更为平滑.直接求差法的结果与整体趋势偏离程度较大,可能是受POS性能的影响(与商用重力仪有一定差距),计算出的姿态角的精度不是足够高,仍对最后的重力扰动结果带来了影响.表2为解算结果与EGM2008模型的较差统计表,从表中我们可以看出,利用状态模型法求出的重力扰动与EGM2008模型的差值中误差为8.27 mGal,利用自适应状态模型法的差值中误差为5.43 mGal,接近GB/T17944-2000《加密重力测量规范》困难地区10 mGal的限差要求.
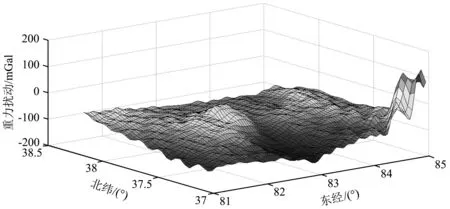
图4 算例1 EGM2008模型计算的重力扰动分布图Fig.4 Gravity disturbance distribution from calculation of model EGM2008 for case 1

差值绝对值最大值差值平均值差值中误差直接求差法29.99-5.3610.13状态模型法19.21-1.158.27自适应状态模型法19.342.445.43
3.2算例2
算例2为对新疆某区平均航高5000 m、航迹140 km、航速分别为145、135、137 m·s-1的三条航线进行航空重力解算,飞行轨迹如图6.飞机在飞行过程中受到的大气扰动较小,三条航线的行高起伏不大.航线经过的区域北部为绿洲,南部为平坦的沙漠,自北向南地面高程逐渐增加,整体无明显起伏.
三条航线的解算结果和EGM2008重力扰动进行作差比较如表3,从表中可以看出,三条航线差值的中误差都在10 mGal左右,与算例1的结论是一致的.

表3 算例2与EGM2008模型较差(单位:mGal)
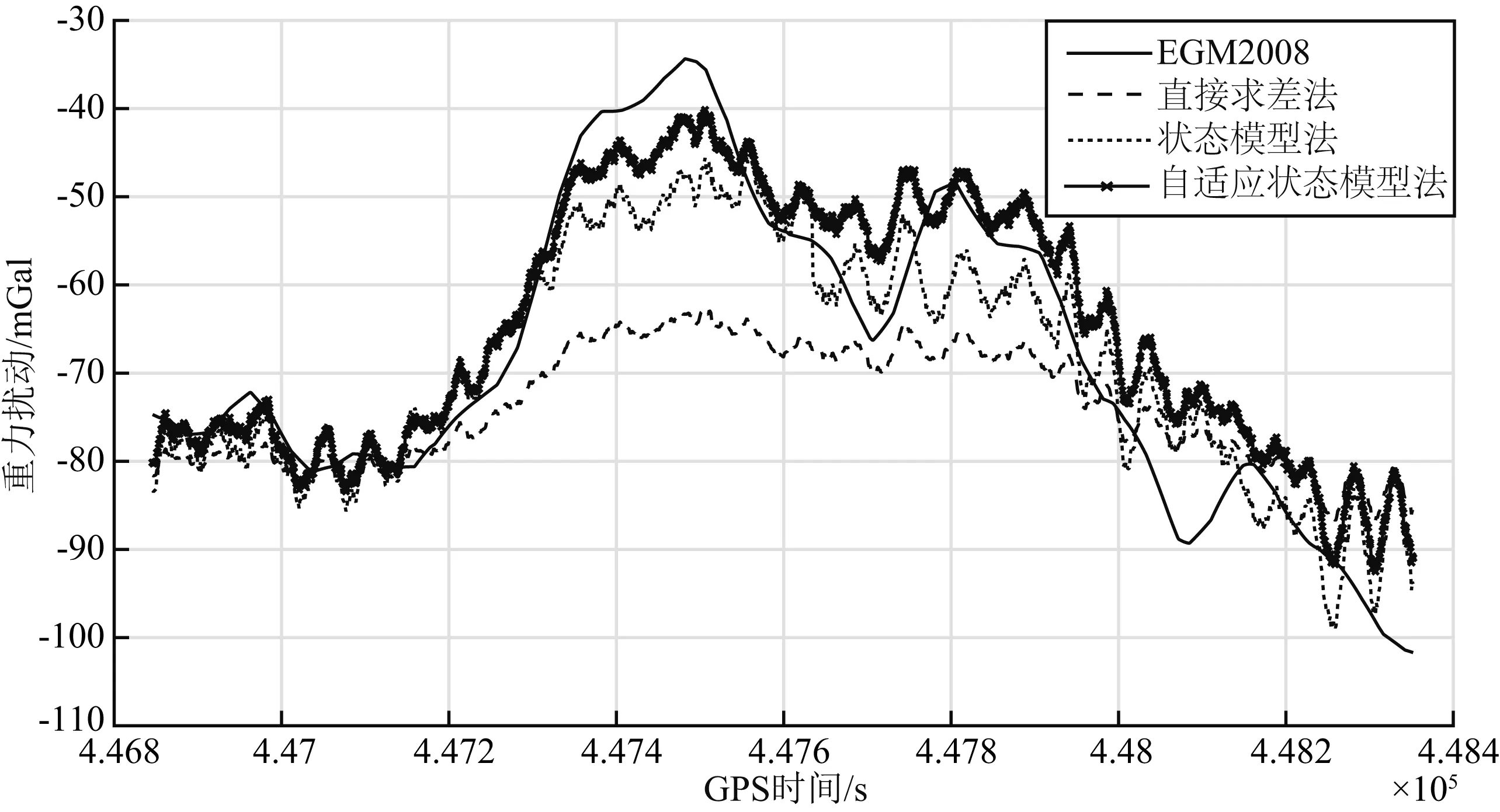
图5 算例1计算的重力扰动与EGM2008模型的重力扰动Fig.5 Gravity disturbance calculated of case 1 in comparison with with model EGM2008

图6 算例2的三条飞行轨迹Fig.6 Three trajectories of flight for case 2
4结论与展望
(1) 利用状态模型法可以有效地获取高精度、高分辨率的空中重力扰动成果,引入自适应因子以后,结果的精度也得到了一定程度的改善;与EGM2008全球重力场模型对比的差值中误差在10 mGal左右,接近国家在困难地区重力测量的精度要求.
(2) 由于采用的惯性系统精度不是很高,未能完全满足直接求差法的要求.从这一点也可以看出状态模型法对设备的性能的要求要低一些.
(3) 受缺少地面重力资料的限制,处理结果仅与开放性的重力场模型进行对比验证,在以后的研究中还需要在含有地面重力资料或高程异常的区域进行航空重力测量,来进一步验证本文提出的方法的有效性.
(4) 利用航空摄影测量任务的POS数据进行航空重力测量分析,提高了数据的利用率,扩展了航空重力测量的方法,在一定程度上节约了航空重力测量的成本.
(5) 基于状态模型法的航空重力测量方法同时还是一种矢量重力测量方法,目前国内还没有成熟的航空矢量重力测量系统,在航空矢量重力数据处理方面也尚处于起步阶段(宁津生,2014),充分吸收国内外现有研究成果,对我国的重力测量事业有非常重要的意义.
References
Bastos L, Yan W, Magalhães A, et al. 2013. Assessment the performance of low cost IMUs for strapdown airborne gravimetry using UAVs.∥ 4th International Colloquium Scientific and Fundamental Aspects of the Galileo Programme. Prague, Czech Republic. Brozena J M, Childers V A. 2000. The NRL Airborne Geophysics Program. Berlin: Springer.
Brozena J M, Mader G L, Peters M F. 1989. Interferometric global positioning system: Three-dimensional positioning source for airborne gravimetry.JournalofGeophysicalResearch:SolidEarth(1978—2012), 94(B9): 12153-12162.
Bruton A M. 2000. Improving the accuracy and resolution of SINS/DGPS airborne gravimetry [Ph. D Thesis]. Canada: University of Calgary.
Chen J Y, Wen H J, Cheng P F. 2001. Some issues of the development of Geodesy in China.AdvanceinEarthSciences(in Chinese), 16(5): 681-688.
Deurloo R A. 2011. Development of a Kalman Filter integrating system and measurement models for a Low-cost strapdown airborne gravimetry system [Ph. D. Thesis]. Porto: University of Porto.
Deurloo R A, Bastos M L, Geng Y, et al. 2011. Evaluation of low- and medium-cost IMUs for Airborne Gravimetry with UAVs.∥ American Geophysical Union, Fall Meeting 2011. San Francisco, California, USA.Forsberg R, Olesen A, Keller K, et al. 2001. Airborne gravity and geoid surveys in the arctic and Baltic Seas.∥ Proceedings of International Symposium on Kinematic Systems in Geodesy, Geomatics and Navigation (KIS-2001). Banff, 586-593.
Gao W G, Yang Y X, Cui X Q, et al. 2006. Application of adaptive Kalman Filtering algorithm in IMU/GPS integrated navigation system. Geomatics and Information Science of Wuhan University (in Chinese), 31(5): 466-469.Gelb A. 1974. Applied Optimal Estimation. Massachusetts: MIT Press. Hajiyev C, Soken H E. 2013. Robust adaptive Kalman Filter for estimation of UAV dynamics in the presence of sensor/actuator faults.AerospaceScienceandTechnology, 28(1): 376-383. Heiskanen W A, Moritz H. 1967. Physical Geodesy. San Francisco: W. H. Freeman & Co.Jekeli C. 2001. Inertial Navigation Systems with Geodetic Applications. Berlin and New York: Walter de Gruyter & Co.
Klingelé E, Halliday M, Cocard M. 1995. Airborne gravimetric survey of Switzerland.∥ 4th International Congress of the Brazilian Geophysical Society.
NIMA. 2000. Department of defense world geodetic system 1984. 3rd ed. National Imagery and Mapping Agency.
Ning J S. 2014. Research on the data processing methods of airborne vector gravimetry using SINS/GNSS.EngineeringSciences(in Chinese), 16(3): 4-13.
Rene F, Olesen A, Munkhtsetseg D, et al. 2007. Downward continuation and geoid determination in mongolia from airborne and surface gravimetry and SRTM topography.∥ International Forum on Strategic Technology, 2007. IFOST 2007. Ulaanbaatar: IEEE, 470-475.Senobari M S. 2010. New results in airborne vector gravimetry using strapdown INS/DGPS.JournalofGeodesy, 84(5): 277-291. Serpas J G, Jekeli C. 2005. Local geoid determination from airborne vector gravimetry.JournalofGeodesy, 78(10): 577-587.
Shi P, Wang X T. 1997. Determination of the terrain surface gravity field using airborne gravimetry and DEM.ActaGeodaeticaEtCartographicaSinica(in Chinese), 26(2): 117-121. Sun Z M. 2004. Theory, method and applications of airborne gravimetry [Ph. D. thesis] (in Chinese). Zhengzhou: Information Engineering University.Sun Z M, Xia Z R, Shi P. 2004a. Progress and advance in airborne gravimetry.ProgressinGeophysics(in Chinese), 19(3): 492-496. Sun Z M, Xia Z R, Shi P, et al. 2004b. Filtering and processing for the airborne gravimetry data.ProgressinGeophysics(in Chinese), 19(1): 119-124. Sun Z M, Zhai Z H, Li Y C. 2013b. Status and development of airborne gravimeter.ProgressinGeophysics(in Chinese), 28(1): 1-8, doi: 10.6038/pg20130101.
Sun Z M, Zhai Z H, Xiao Y, et al. 2013a. Systematic error compensation for airborne gravimetry.ChineseJournalofGeophysics(in Chinese), 56(1): 47-52, doi: 10.6038/cjg20130105. Titterton D H, Weston J L. 2004. Strapdown Inertial Navigation Technology. Stevenage: The Institution of Electrical Engineers. Tomé P. 2002. Integration of inertial and satellite navigation systems for aircraft attitude determination [Ph. D Thesis]. Porto: University of Oporto. Verdun J, Bayer R, Klingelé E E, et al. 2002. Airborne gravity measurements over mountainous areas by using a LaCoste & Romberg air-sea gravity meter.Geophysics, 67(3): 807-816.
Xia Z R, Shi P, Sun Z M, et al. 2004. Chinese airborne gravimetry system CHAGS.ActaGeodaeticaetCartographicaSinica(in Chinese), 33(3): 216-220.
Yang J Y, Zhang X H, Zhang F F. 2012. On the accuracy of EGM2008 earth gravitational model in Chinese mainland.ProgressinGeophysics(in Chinese), 27(4): 1298-1306, doi: 10.6038/j.issn.1004-2903.2012.04.003.
Yang Y, He H, Xu G. 2001. Adaptively robust filtering for kinematic geodetic positioning.JournalofGeodesy, 75(2-3): 109-116.
Yang Y X. 2006. Adaptive Navigation and Kinematic Positioning (in Chinese). Beijing: Surveying and Mapping Press.
Yang Y X, Gao W G. 2006a. An Optimal Adaptive Kalman Filter.JournalofGeodesy, 80(4): 177-183.
Yang Y X, Gao W G. 2006b. A new learning statistic for adaptive filter based on predicted residuals.ProgressinNaturalScience, 16(8): 833-837.
Zhang C D. 2005. On the subject of airborne gravimetry and airborne gravity gradiometry.ChineseJournalofEngineeringGeophysics(in Chinese), 2(4): 282-291.
Zhang C Y, Guo C X, Chen J Y, et al. 2009. EGM 2008 and its application analysis in Chinese Mainland.ActaGeodaeticaetCartographicaSinica(in Chinese), 38(4): 283-289.
Zhou J X, Liu H J, Wang S T. 2003. The prediction of China airborne gravimetry in geophysics.∥ China Geophysical Society 19th Annual Conference (in Chinese). Beijing: Chinese Geophysical Society.
附中文参考文献
陈俊勇, 文汉江, 程鹏飞. 2001. 中国大地测量科学发展的若干问题. 地球科学进展, 16(5): 681-688.
高为广, 杨元喜, 崔先强等. 2006. IMU/GPS组合导航系统自适应Kalman滤波算法. 武汉大学学报(信息科学版), 31(5): 466-469. 宁津生. 2014. 基于SINS/GNSS的航空矢量重力测量数据处理方法研究. 中国工程科学, 16(3): 4-13.
石磐, 王兴涛. 1997. 利用航空重力测量和DEM确定地面重力场. 测绘学报, 26(2): 117-121.
孙中苗. 2004. 航空重力测量理论、方法及应用研究[博士论文]. 郑州: 解放军信息工程大学.
孙中苗, 夏哲仁, 石磐. 2004a. 航空重力测量研究进展. 地球物理学进展, 19(3): 492-496.
孙中苗, 夏哲仁, 石磐等. 2004b. 航空重力测量数据的滤波与处理. 地球物理学进展, 19(1): 119-124.
孙中苗, 翟振和, 李迎春. 2013b. 航空重力仪发展现状和趋势. 地球物理学进展, 28(1): 1-8, doi: 10.6038/pg20130101.
孙中苗, 翟振和, 肖云等. 2013a. 航空重力测量的系统误差补偿. 地球物理学报, 56(1): 47-52, doi: 10.6038/cjg20130105.
夏哲仁, 石磐, 孙中苗等. 2004. 航空重力测量系统CHAGS. 测绘学报, 33(3): 216-220.
杨金玉, 张训华, 张菲菲等. 2012. EGM2008地球重力模型数据在中国大陆地区的精度分析. 地球物理学进展, 27(4): 1298-1306, doi: 10.6038/j.issn.1004-2903.2012.04.003.
杨元喜. 2006. 自适应动态导航定位. 北京: 测绘出版社.
张昌达. 2005. 航空重力测量和航空重力梯度测量问题. 工程地球物理学报, 2(4): 282-291.
章传银, 郭春喜, 陈俊勇等. 2009. EGM 2008地球重力场模型在中国大陆适用性分析. 测绘学报, 38(4): 283-289.
周坚鑫, 刘浩军, 王守坦. 2003. 航空重力测量在我国地球物理勘探中的应用展望.∥ 中国地球物理学会第十九届年会论文集. 北京: 中国地球物理学会.
(本文编辑张正峰)
Introducing the optimal adaptive factor to improve the accuracy of airborne gravimetry based on the state model method
YAN Wen-Lin1,2, LI Ying-Cheng1,3, XUE Yan-Li1,3
1ChinaTopRSTechnology,Beijing100039,China2InstituteofSpaceSciences,ShandongUniversity,ShandongWeihai264209,China3ChineseAcademyofSurveyingandMapping,Beijing100830,China
AbstractThis work introduced the optimal adaptive factor to improve the accuracy of airborne gravimetry based on the state model method, attempted to apply this technique to areas of China where gravity measurement is difficult. Gravity disturbance was used as the state vector of Kalman Filter, and the optimal adaptive factor was introduced to adjust the weight matrix of the state information to improve the accuracy of estimation of the gravity disturbance. Based on flight data at different times and different heights in Xinjiang, this work calculated the vertical gravity disturbances, and compared them with the EGM2008 global gravity model. The differences between the results from the proposed method and the EGM2008 model are around 10 mGal, which is close to the precision demand of national gravity surveys in difficult areas.
KeywordsAirborne gravimetry; State model method; Kalman Filter; Adaptive factor
基金项目航空遥感技术国家测绘地理信息局重点实验室开放研究课题 (航空遥感的POS数据在航空重力测量中的应用),国家自然科学基金资助项目(41274042)和国家自然科学基金资助项目(41504032)联合资助.
作者简介闫文林,男,1984年生,博士研究生,测绘中级工程师,主要从事航空重力测量、组合导航、GNSS精密定位及摄影测量算法等技术的研究. E-mail: yanwenlin1984@163.com
doi:10.6038/cjg20160409 中图分类号P223
收稿日期2014-09-11,2015-06-16收修定稿
闫文林, 李英成, 薛艳丽. 2016. 引入最优自适应因子的状态模型法航空重力测量.地球物理学报,59(4):1267-1274,doi:10.6038/cjg20160409.
Yan W L, Li Y C, Xue Y L. 2016. Introducing the optimal adaptive factor to improve the accuracy of airborne gravimetry based on the state model method.ChineseJ.Geophys. (in Chinese),59(4):1267-1274,doi:10.6038/cjg20160409.

