欧拉方程组径向对称正规解的爆破

朱旭生，汤传扬，王　莉

(华东交通大学理学院，江西 南昌 330013)

欧拉方程组径向对称正规解的爆破

朱旭生，汤传扬，王莉

(华东交通大学理学院，江西 南昌 330013)

[摘要]研究了N维可压缩欧拉方程组真空问题径向对称正规解的爆破问题，利用积分法得出该问题非平凡径向对称正规解(ρ，v)在有限时间内发生爆破.

[关键词]欧拉方程组；径向对称；正规解；积分法；爆破

1预备知识

本文考虑N维可压缩欧拉方程组

(1)

在满足初始条件

(2)

(ⅰ)(ρ，u)(x，t)∈C1(Rn×[0，T))；

(ⅱ)P(ρ)(x，t)∈C1(Rn×[0，T))；

(ⅲ)在ρ的紧支集之外，u满足

(3)

关于欧拉方程经典解的爆破问题在一些文献中已有讨论：文献[1-2]讨论初值问题解的爆破；文献[3-6]讨论了真空情形经典解的爆破，其中文献[3-5]讨论了正规解的爆破，文献[6]利用平面自治系统定性理论研究了径向对称(有时也称轴对称或球对称)解的爆破；文献[7-12]讨论了真空情况下欧拉方程组或带排斥力的欧拉泊松方程径向对称解的爆破问题.这些文献研究的大多是初值问题，只有文献[6，13]研究的是初边值问题.

(4)

将(4)式代入(1)式中得

(5)

其相应的初始条件为

(6)

相应地，当0≤r0；当r≥R1时，ρ0(r)=0.对初值v0(r)，我们假设当r≥R2时v0(r)=0，这里R2≥R1.对于径向对称的欧拉方程组的正规解，除满足(ρ，u)(x，t)∈C1(Rn×[0，T))外，在ρ的紧支集外(4)式变为

vt+VVr=0.

(7)

当然，为了去掉在x=0处的奇性，要求v(0，t)=0，vr(r，t)=o(r).

2主要结论及证明

定理1设(ρ，v)是N维欧拉方程组初值问题(1)—(2)在真空条件下的非平凡经典解，即做径向变换后(5)—(6)的经典解.假设suppρ0⊆{r|r≤R2}，当r≥R2时v0(r)=0，且

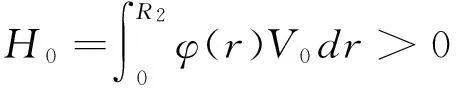
(8)

证明首先处理真空边界.设suppρ(r，t)={r|r≤R1(t)}，由于函数v∈C1，故由(7)式可知R1(t)满足

(9)

将上式两端关于t求导，并由(7)式得

从而

R1(t)=R1(0)+v(R1(0)，0)t=R1+v0(R1)t.

(10)

其次，引入随体导数

(11)

利用(11)式可以将(1)式第一个方程改写为

(12)

(13)

下面处理速度为零的边界点.由于点R2也落在suppρ0外，故此处也满足(7)式，从而

同样解得

R2(t)=R2+v0(R2(0))t=R2.

(14)

将压强函数P=P(ρ)=Kργ代入(6)式第二个方程得

ρ(vt+VVr)+Kγργ-1ρr=0.

(15)

当0≤r0，故

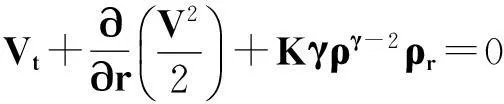
(16)

由于γ>1，故ργ-1(r，t)∈C([0，+∞)×[0，T))，且当rR1(t)时，ργ-1∈C1.当1<γ<2时，ργ-1在r=R1(t)处关于r不可导，但∂r(ργ-1)在r=R1(t)处具有可积的奇性，因此在做积分时我们可以认为(16)式对任意区域均成立.

引入函数φ(r)≥0，φ(r)∈C1([0，R2))，φ′(r)>0.将(16)式两端同乘以φ(r)，

(17)

(18)

即

(19)

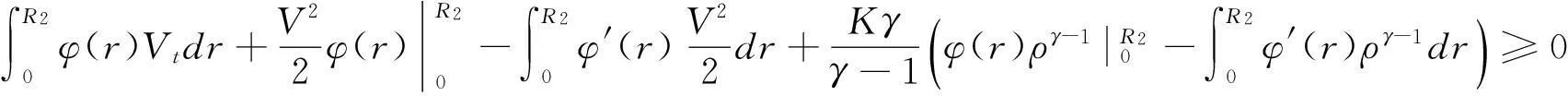
(20)

利用v(R2，t)=ρ(R2，t)=0，(20)式可改写为

(21)

这里因为φ′(r)>0，K≥0且γ>1，从而

(22)

(23)

令

(24)

则(23)式化简为

(25)

进一步由Cauchy-Schwarz不等式得

(26)

令

(27)

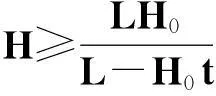
(28)

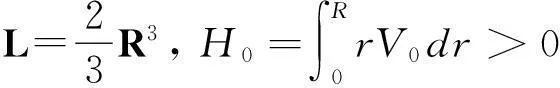
注2如果R1=R2=R，我们的结论与文献[12]中当R(t)=R时的结论一致.

[参考文献]

[1]ALINHAC S.Blowup for nonlinear hyperbolic equations[M].Boston：Birkhauser，1995:33-36.

[2]SIDERIS T.Formation of singularities in three-dimensional compressible fluids[J].Comm Math Phys，1985，101：475-485.

[3]LIU T P，YANG T.Compressible Euler equations with vacuum[J].J Differential Equations，1997，140:223-237.

[4]MAKINO T，UKAI S，KAWASHIMA S.Sur la solution à support compact de l’équation d’Euler compressible[J].Japan J Indust Appl Math，1986(3)：249-257.

[5]ZHU XUSHENG，WANG WEIKE.The regular solutions of the isentropic Euler equations with degenerate linear damping[J].Chinese Ann Math B，2005，26(4)：583-598.

[6]LI T，WANG D.Blowup phenomena of solutions to the Euler equations for compressible fluid flow[J].J Differential Equations，2006，221：91-101.

[7]ZHU XUSHENG，TU AIHUA.Blowup of the axis-symmetric solutions for the IBVP of the isentropic Euler equations[J].Nonlinear Analysis：Theory，Methods & Applications，2014，95:99-106.

[8]YUEN M W.Blowup for the Euler and Euler-Poisson equations with repulsive force[J].Nonlinear Analysis Series A：Theory，Methods & Applications，2011，74:1465-1470.

[9]PERTHAME B.Nonexistence of global solutions to Euler-Possion equations for repulsive force[J].Japan J Appl Math，1990，7(2):363-367.

[10]MAKINO T.Blowing up solutions of the Euler-Poisson equations for the evolution of the gaseous stars[J].Transport Theory and Statistical Physics，1992，21:615-624.

[11]DENG Y B，XIANG J L，YANG T.Blowup phenomena of solutions to Euler-Poisson equations[J].J Math Anal Appl，2003，286:295-306.

[6]CHAE D H，TADMOR E.On the finite time blow-up of the Euler-Poisson equations of in RN[J].Commun Math Sci，2008，6:785-789.

[12]LI RUI，LIN XING，MA ZONGWEI，et al.Improved blow-up results for the Euler and Euler-Poisson equations with repulsive forces[J].J Math Anal Appl，2014，417：57-64.

[13]朱旭生，陈家乐，汤传扬.可压缩等熵欧拉方程组外问题的爆破[J].华东交通大学学报，2014(3)：105-109.

[14]胡卫敏，伊磊，陈维.一类分数阶微分方程三点边值问题的多重正解[J].东北师大学报(自然科学版)，2011，43(2):16-22.

[15]栾姝，徐鹏.一类串联系统的边界Carleman估计[J].东北师大学报(自然科学版)，2011，43(2):39-45.

(责任编辑：李亚军)

Blowup of the radial symmetric regular solution for the Euler equations

ZHU Xu-sheng，TANG Chuan-yang，WANG Li

(School of Science，East China Jiaotong University，Nanchang 330013，China)

Abstract:The blowup of the radial symmetric regular solutions for the N-dim compressible Euler equations is studied，while the initial flow is vacuum outside a ball.Under some assumptions，it is shown that the non-trivial classical solutions (ρ，V)blowup on or before the finite time .

Keywords:Euler equations；radial symmetry；regular solution；integration method；blowup

[文章编号]1000-1832(2016)02-0031-04

[收稿日期]2014-10-15

[基金项目]国家自然科学基金资助项目(11161021，61262031，11326139);江西省科技厅项目(20142BAB211010).

[作者简介]朱旭生(1968—)，男，副教授，主要从事偏微分方程研究；汤传扬(1989—)，男，硕士，主要从事偏微分方程研究.

[中图分类号]O 175.27[学科代码]110·4720

[文献标志码]A

[DOI]10.16163/j.cnki.22-1123/n.2016.02.008