Poisson代数分解唯一性

张文慧，唐鑫鑫，于海燕，徐兰兰

(东北师范大学数学与统计学院，吉林 长春 130024)

Poisson代数分解唯一性

张文慧，唐鑫鑫，于海燕，徐兰兰

(东北师范大学数学与统计学院，吉林 长春 130024)

[摘要]给出了Poisson代数T的子代数、理想、同态等基本定义，通过引入T的T-自同态，得到具有平凡中心Poisson代数的分解在不计次序的条件下是唯一的.

[关键词]Poisson代数；T-自同态；分解

1预备知识

分解唯一性在分析代数结构上具有重要的作用，自文献[6]中给出了完备李代数的分解唯一性证明后，接着n-李代数，李三系，二次李超三系的分解唯一性也在文献[7-9]中得到了证明.本文受李代数的启发通过定义出具有双代数结构Poisson代数的自同态，指出其分解在不计次序的条件下是唯一的.

文中域F的特征数ChF≠2，所研究的Poisson代数均是有限维的.

则称T是域f上的李代数.

则称T是域f上的Poisson代数.

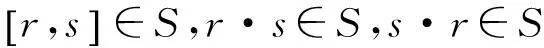
2主要结果及证明

定理1设T1，T2，…，Tn是Poisson代数T的理想，并且T有理想的直和分解T=T1⨁T2…⨁Tn，则下列结果成立：

(2)如果S是Ti的理想，则S也是T的理想.

则称Lx，rx分别是左右点乘变换，λx，ρx为左右括积变换.

根据Poisson代数定义可以得到：

ρxρy=ρ[y，x]+ρyρx，λx+ρx=0;

λx·y=ryλx+Lxλy，ρxLy=Lyρx+L[y，x].

定义5设T是域f上Poisson代数，S是其子集.则称

为S在T中的零化子.

定理2若S是T的理想，则Cs也是T的理想.

证明设x∈Cs，y∈T，z∈S，

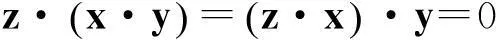
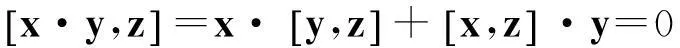
所以x·y∈Cs，同理，y·x∈Cs.又因为

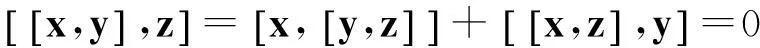
定义6设T和L都是Poisson代数.如果T到L的线性映射f满足：

定义7如果一个Poisson代数T的自同态f满足

flx=Lxf，frx=rxf，fλx=λxf，fρx=ρxf，∀x∈T，

则称f是T的T-自同态.

设T是域f上Poisson代数，并且有分解T=T1⨁T2，其中T1，T2是T的理想，π1是T到T1的投影，则π1是T的T-自同态.

事实上，设x=x1+x2，y=y1+y2，xi，yi∈Ti，i=1，2.则

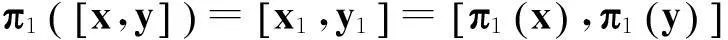
引理1设T是域f上的Poisson代数.则下列命题成立：

通过类似的推导即可完成证明.

μμ-1=μ-1μ=IdT，μ-1rx=μ-1rxμμ-1=μ-1μrxμ-1=rxμ-1，

同理可得

μ-1Lx=Lxμ-1，μ-1λx=λxμ-1，μ-1ρx=ρxμ-1.

引理2设T是域f上Poisson代数，并且有分解T=T1⨁T2，其中T1，T2是T的理想.则：

(1)CT有理想的分解

CT=CT1⨁CT2;

(1)

(2)若CT=0，则

T1=CT2，T2=CT1.

(2)

证明(1)设x=x1+x2∈CT，其中xi∈Ti，i=1，2.则

所以x1∈CT1，同理x2∈CT2，故CT⊆CT1+CT2.

反之，设x1+x2∈CT1+CT2，其中xi∈CTi.任意y=y1+y2∈T，其中yi∈Ti，i=1，2，有

即x1+x2∈CT，故CT=CT1+CT2.易得CT1，CT2均是CT的理想并且CT1∩CT2=0，故结论成立.

由于CT2=0，故x2=0，CT2⊆T1，从而T1=CT2.同理可得T2=CT1.

证明此引理证明很容易，故略去.

引理4设T是域f上Poisson代数，μ是T的T-自同态.则存在某个确定的n∈N，使得：

(1)T可分解为理想直和T=Imμn⨁Kerμn;

注意到

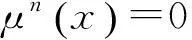
Imμn∩Kerμn=0，T=Imμn+Kerμn.

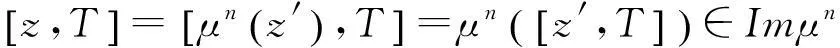
故Imμn是T的理想，类似可以证明Kerμn也是T的理想，从而结论成立.

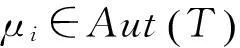
证明对n用数学归纳法来证明.

这与μ1+μ2=IdT矛盾.

注引理中T不可分解的限制条件不可缺少.若T=T1⨁T2，π1，π2分别是T到T1，T2的投影，由前面的证明可知π1，π2是T的T-自同态，且π1+π2=IdT，但显然π1，π2不是单射.

定理3设T是域f上Poisson代数，CT=0.则下列命题成立：

(1)T可分解成不可分解理想之和；

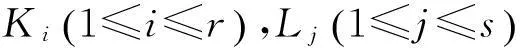
证明(1)因为T的维数是有限维的，故对T的维数用数学归纳法即可得证.

(2)对r用归纳法来证明此定理.当r=1时T=K1不可分解，所以s=1，T=K1=L1.

设

事实上，任意x，y∈K1，

同理

是K1的K1-自同态.

任意z∈K1，有

设K=K2⨁K3⨁…⨁Kr，L=L2⨁L3⨁…⨁Ls.根据引理2

K=CK1，K1=CK，L=CL1，L1=CL，Kerδ1=L.

[参考文献]

[1]SU YUCAI，XU XIAOPING.Central simple Poisson algebras [J].Science in China，2004，47(2)：245-263.

[2]SHENG YUNHE.Representations of Hom-Lie algebras [J].Algebras and Representation Theory，2012，15 (6)：1081-1098.

[3]王圣祥，董丽红.一类广义李代数的Engle 定理 [J].东北师大学报(自然科学版)，2013，45(4)：36-40.

[4]靳全勤，佟洁.Toroidal 李代数上的Poisson代数结构 [J].数学年刊，2007，28A：57-70.

[5]CASAS J M.Noncommutative Leibniz Poisson algebras [J].Communications in Algebra.2006，34(7)：2507-2530.

[6]孟道骥，朱林生，姜翠波.完备李代数 [M].北京：科学出版社，2001：30-38.

[7]白瑞蒲，孟道骥.n-Lie代数的分解及唯一性 [J].数学年刊，2004，25A(2)：147-152.

[8]孟道骥，史毅茜.李三系分解的唯一性[J].数学进展，2004，18(1)：52-56.

[9]潘玉霞，张庆成，冯闪，等.二次李超三系分解的唯一性[J].东北师大学报(自然科学版)，2012，44(2)：9-13.

[10]LARSSON D，SILRESTROV S D.Quasi-Hom-Lie algebra，central extensions and 2-cocycle-like identities [J].J Algebra，2005，288(2)：321-344.

(责任编辑：李亚军)

The uniqueness of the decomposition of Poisson algebra

ZHANG Wen-hui，Tang Xin-xin，YU Hai-yan，XU Lan-lan

(School of Mathematics and Statistics，Northeast Normal University，Changchun 130024，China)

Abstract:Necessary definitions are presented，such as subalgebras，ideals，homomorphism in Poisson algebras.Then by introducing T-endomorphisms，the uniqueness of the decomposition of Poisson algebras with trival center without considering the order is obtained.

Keywords:Poisson algebras；T-endomorphism；decomposition

[文章编号]1000-1832(2016)02-0006-05

[收稿日期]2014-10-21

[基金项目]国家自然科学基金资助项目(11171055)；吉林省自然科学基金资助项目(201301068JC).

[作者简介]张文慧(1989—)，女，硕士，主要从事李代数研究.

[中图分类号]O 152.5[学科代码]110·21

[文献标志码]A

[DOI]10.16163/j.cnki.22-1123/n.2016.02.002