线结构光传感器测头参数优化与物镜设计

殷 欢 合肥工业大学仪器科学与光电工程学院 安徽合肥 230009



线结构光传感器测头参数优化与物镜设计

殷 欢 合肥工业大学仪器科学与光电工程学院 安徽合肥 230009

【文章摘要】

线结构光传感器测头是非接触三维测量的关键部件，测量精度影响三维位置信息提取的准确性。本文基于激光三角法建立线结构光测头的数学模型，基于透视投影建模完成成像坐标系与世界坐标系的转换。研究系统综合测量误差与结构参数的关系，给出目标方程与边界函数，用matlab软件对结构参数仿真与优化。选取合适的结构参数后用zemax软件设计满足要求的物镜结构。

【关键词】

线结构光；数学模型；结构参数；matlab；zemax

0　引言

随着工业对测量精度要求越来越高，利用光学技术进行非接触测量是最具潜力的三维测量方法。其优点是系统柔性好、量程大、速度与精度适中。线结构光传感器基于激光三角法，激光器将结构光投影到三维物体，再以一定角度漫反射回位置探测器，由探测器接收面位移算出物体表面点的三维坐标。系统结构决定测量范围与精度，分析结构参数对结果的影响十分必要。

本文基于激光三角法建立测头数学模型，透视投影建模转换成像坐标系与世界坐标系，研究系统综合测量误差与结构参数的关系，给出目标方程与边界函数，结合非线性规划思想用matlab对结构参数仿真优化。选取合适的结构参数后用zemax设计满足要求的物镜结构。

1　线结构光传感器测头数学模型的建立

图1　透视投影测量原理图

构造测头数学模型是本文的关键内容。三角法是从光源发射光线到被测表面，在另一向透镜成像观察入射点位置，入射与反射光线空间位置成三角形。按入射光与被测目标法线间角度关系分为直射式和斜射式。直射法建模具有代表性，本文选择分析直射法，透视投影建立数学模型。透视投影变换在齐次坐标下进行，测量原理如图1所示。

图1中Ow-XwYwZw和Oc-XcYcZc为世界坐标系和摄像坐标系，是三维空间坐标系；O-XY为物体成像二维坐标系；X、Y轴平行于Xc、Yc轴。世界坐标系由摄像坐标系与光切平面唯一确定。Zc轴斜向下与光切平面交点为世界坐标系原点Ow；Zw轴在光切平面内垂直向上，在Zc轴和Xc轴决定的平面内；Yw轴在光切平面内与Yc轴平行；Xw轴垂直于光切平面。物体曲线方程为：

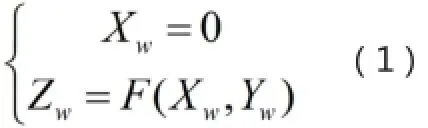
视场内线段经物镜成像在像平面，物体表面在Zw轴偏离XwOwYw平面使光线成像与Y轴不重合，偏移量由Zw值决定。本文要建立世界坐标系点P（0，Yw，Zw）与摄像坐标系点P’（Xi，Yi，-f）的关系式，f为摄像物镜焦距。把世界坐标点写成齐次坐标形式（Xw，Yw，Zw，1），摄像坐标点为（Xc，Yc，Zc，1），世界坐标系经坐标平移使Ow与Oc重合，绕X轴旋转180°，再绕Y轴旋转-θ（右手坐标系从正半轴向原点看逆时针是正方向，这里按右手定则是反方向取负号）后转换成摄像坐标系。表达式如下：

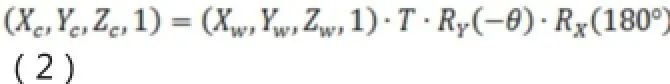
式中RY（-θ）和RX（180°）代表绕Y轴和X轴旋转的矩阵，T代表平移矩阵，其表达如下：

将世界坐标系光切平面坐标点集（0，Yw，Zw，1）带入公式（2），Yw、Zw为未知量，得摄像坐标点集：

将图像坐标系P’点转换到摄像坐标系，齐次坐标形式表示（Xi，Yi，-f，1），联立公式，结合，得世界坐标系光切平面点和摄影坐标系图像传感器点之间的关系式：

式中（Xw，Yw，Zw）为世界坐标系被测物体点的坐标，（Xi，Yi，-f）为图像坐标，θ为物镜光轴与光切平面夹角，L是物镜中心到光切平面垂直距离，在透视坐标系下便于分析外部参数L、θ。

2　线结构光传感器测头结构参数分析与优化

本节利用数学模型分析结构参数，给出约束条件，根据主要影响因子进行优化设计，结合实例给出最优参数，尽量使测量误差达到最小。

2.1结构参数设计分析

测量模型中世界坐标系Yw和Zw是L、θ、f、Xi和Yi的函数，根据误差理论分析得Yw和Zw测量误差与各自变量有关，可得：

其中ΔL、Δθ、Δf是结构参数L、θ、f的标定误差，ΔXi和ΔYi为像面坐标Xi和Yi提取误差。系统综合测量误差△为：

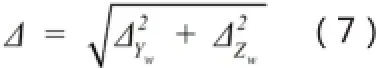
有两种因素影响被测表面点坐标测量误差：结构参数L、θ、f的标定误差和图像处理中像点坐标提取误差。给定系统参数固定不变，使用前精确标定，因此ΔL、Δθ、Δf影响很小，主要误差是像点坐标提取误差。实际中像点坐标提取误差随算法改变，在此令ΔXi和ΔYi为一定值δ。利用式（5）Yw、Zw坐标分别对Xi、Yi求偏导，得被测面上点在Yw、Zw轴方向测量误差，再由式（7）得系统综合测量误差：

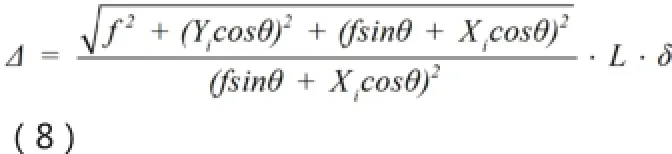
由上得△随被测点位置不同而改变，在物面分布不均匀；△值随f和θ增加单调减小，随L和δ增加单调增加。设图像传感器尺寸2CX×2CY，Xi∈［-CX，CX］、Yi∈［-CY，CY］；得△在Xi=-CX，Yi=±CY时最大。要在视场内测量精度都达标，即△最大时要符合要求，得：

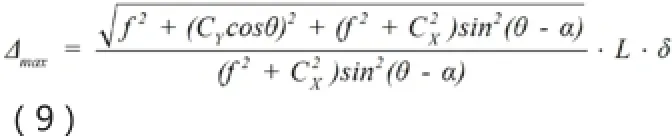
式中θ为线激光漫反射到物镜的角度，实际要考虑光能量，把漫反射光条近似为郎伯辐射体，光条辐射强度满足余弦定理，随θ余弦变化，当θ为90°光强为0，即θ不能太大，否则不能捕捉清晰图像。式中α为视场半角小于θ值，即，实际中图像传感器不能探测无穷远处物点。当CX、CY已知，△max为L、f、θ的函数，把公式（9）定为结构目标函数，常取最小值时的结构参数量。当像面尺寸已知，由公式（5）可得Zw、Yw最小值和最大值。

2.2设计实例

本文设计一个轻型线结构光测头，提出设计指标：综合测量误差小于0.020mm，测量深度范围80-120mm，宽度范围50-80mm，响应速度快，外形尺寸紧凑。

本文选取Thorlabs L650P007型号TO封装半导体激光器，标准光输出功率7mW，标准波长650nm，门限电流20mA，正常工作电流和电压为28mA和2.2V，垂直方向半光束发散角28°，平行方向半光束发散角9°，最大象散值15μm，监测电流0.12mA。数字图像传感器选用Aptina IMAGING MT9P031型号1/2.5-Inch 5Mp CMOS传感器，像面尺寸5.70×4.28mm，对角线长7.13mm，像元大小2.2×2.2μm，有效像素2592H×1944V，最高帧率53fps，支持数字和模拟信号输出。常用工业镜头焦距有8mm、12mm、16mm、25mm，取像素提取误差为1/4个像元尺寸，将已知参数带入目标函数与约束方程，优化出合适的结构参数。基本约束：传感器尺寸L为70-120mm，θ值大于α，由焦距与图像传感器尺寸确定。

此优化模型为非线性规划问题，用matlab对结构参数仿真优化，由于选取初值不确定，可得多组满足要求的结构参数，表1只列出不同焦距f的部分仿真数据：

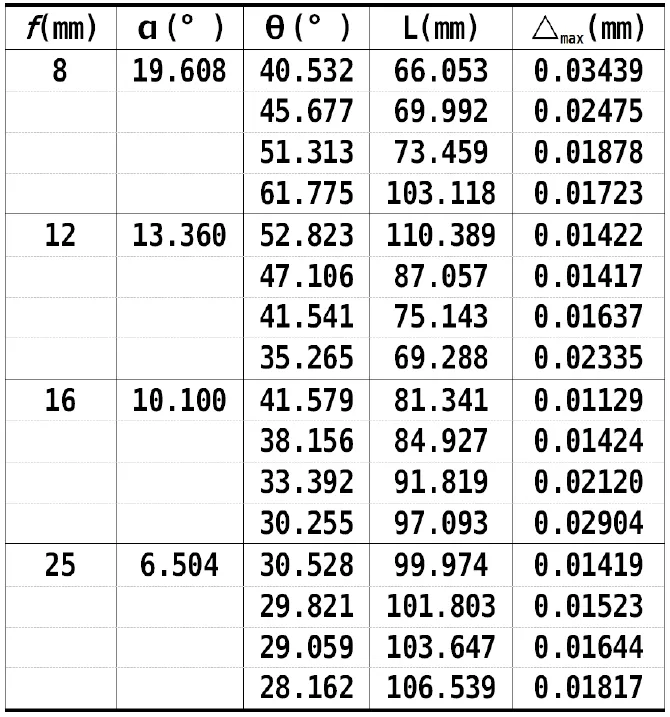
表1　不同f值下结构参数部分仿真结果

由图2得综合测量误差与结构参数L、θ的关系，L与△max呈线性关系，△max随L增大而增大；焦距与△max呈非线性关系，一定范围内△max值随f增加而降低。综合考虑相机视场、测头尺寸和设计要求，从仿真结果中选取合适的结构参数：f =12mm，θ=47°，L=87mm，△max=0.01417mm，满足要求。

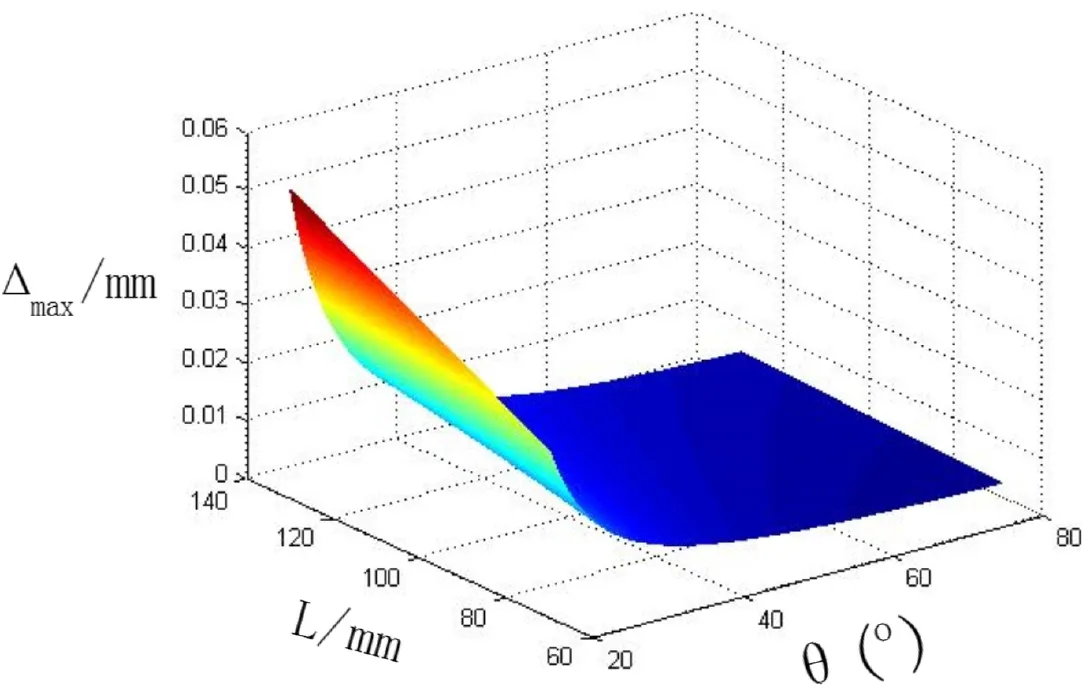
图2　综合测量误差与L、θ关系图

3　线结构光传感器测头物镜设计

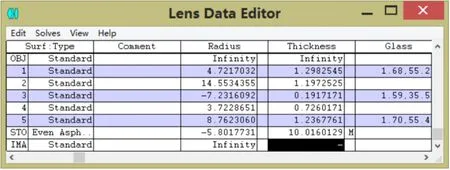
图3　系统结构数据图

摄影物镜光学特性由焦距f、相对孔径和视场角共同决定。焦距为12mm；相对孔径由像面照度和物镜分辨率决定，普通摄影物镜为1：9～1：2.8，CMOS传感器对角线ymax为7.13mm，得相对孔径D/f’=1：3.37，实际设计取更大值；视场角由焦距和像面大小决定，半视场角ω=arctan（ymax/2f’）=16.54°，视场角2ω=33.08°。本文从光学设计手册选取近似结构，通过缩放焦距法得到初始结构。

查询后选定初始结构为后置光阑的三片物镜，初始参数：焦距f’=42.12mm，相对孔径1：2.8，视场角2ω=54°。初始结构效果一般，要添加MTFA、MTFT、MTFS操作数控制衍射调制函数在空间频率内高于一定值，也要添加镜片边界函数控制各镜片中心和边缘厚度，还要添加像差操作数SPHA、COMA、ASTI、DIST等来控制系统基本像差，然后根据实际情况添加TTHI、OPGT等操作数来进行优化，得到最终结构如图3-8：

系统第6面采用非球面，其余面是标准球面，在zemax中用合适的优化函数和操作数校正像差，逐步进行像差平衡，获得实际焦距12.011mm的物镜镜头，总畸变不超过0.4%，所选视场内MTF轴上超过70%@100lp/mm，轴外0.7071超过35%@100lp/mm，MTF曲线比较理想，整个系统球差0.000223，彗差-0.002911，像散-0.000304，镜头总长14.666mm，镜头结构紧凑，像质较好，满足设计要求。

4　总结

在线结构光传感器测头数学模型基础上分析各结构参数对综合测量误差的影响，综合考虑测量精度和像素提取误差，建立优化目标方程和边界条件，结合非线性规划思想用matlab软件对结构参数仿真优化，得到理想的结构参数，再用zemax软件设计满足要求的物镜结构，对线结构光传感器测头结构参数优化与物镜设计有理论指导意义。

【参考文献】

［1］王宝光，贺忠海，陈林才，等.结构光传感器模型及特性分析［J］.光学学报，2002，22（4）：481-484.

［2］张广军，王红，赵慧洁，等.结构光三维视觉系统研究［J］.航空学报，1999（4）：78—80.

［3］熊会元，陈承鹤，宗志坚.线结构光视觉传感器设计优化［J］.工具技术，2009（9）：81—83.

［4］金文燕，赵辉，陶卫.激光三角测距传感器建模及参数优化研究［J］.传感技术学报，2006，19（4）：1090-1093.

［5］Zhang Jianxin，Djordjevich Alexandar.Study on laser stripe sensor［J］.Sensors and Actuators，1999，72（3）：224—228.

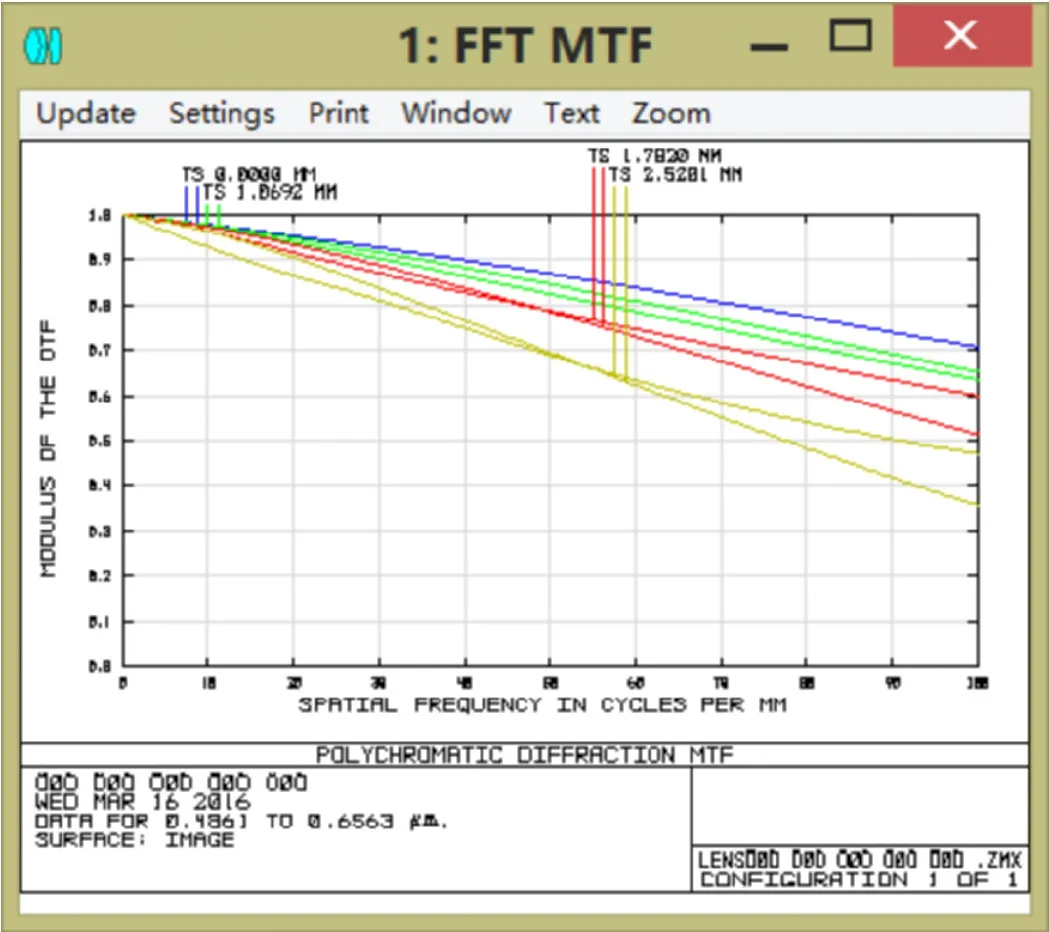
图4　MTF曲线图

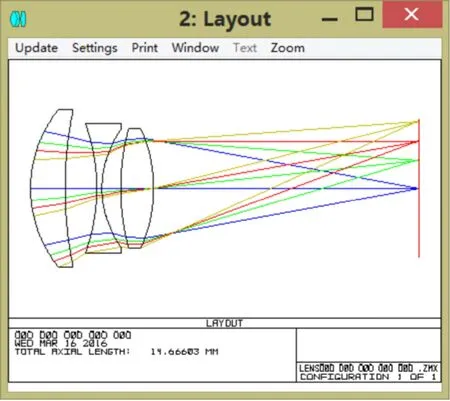
图5　成像系统结构图

图6　场曲和畸变图

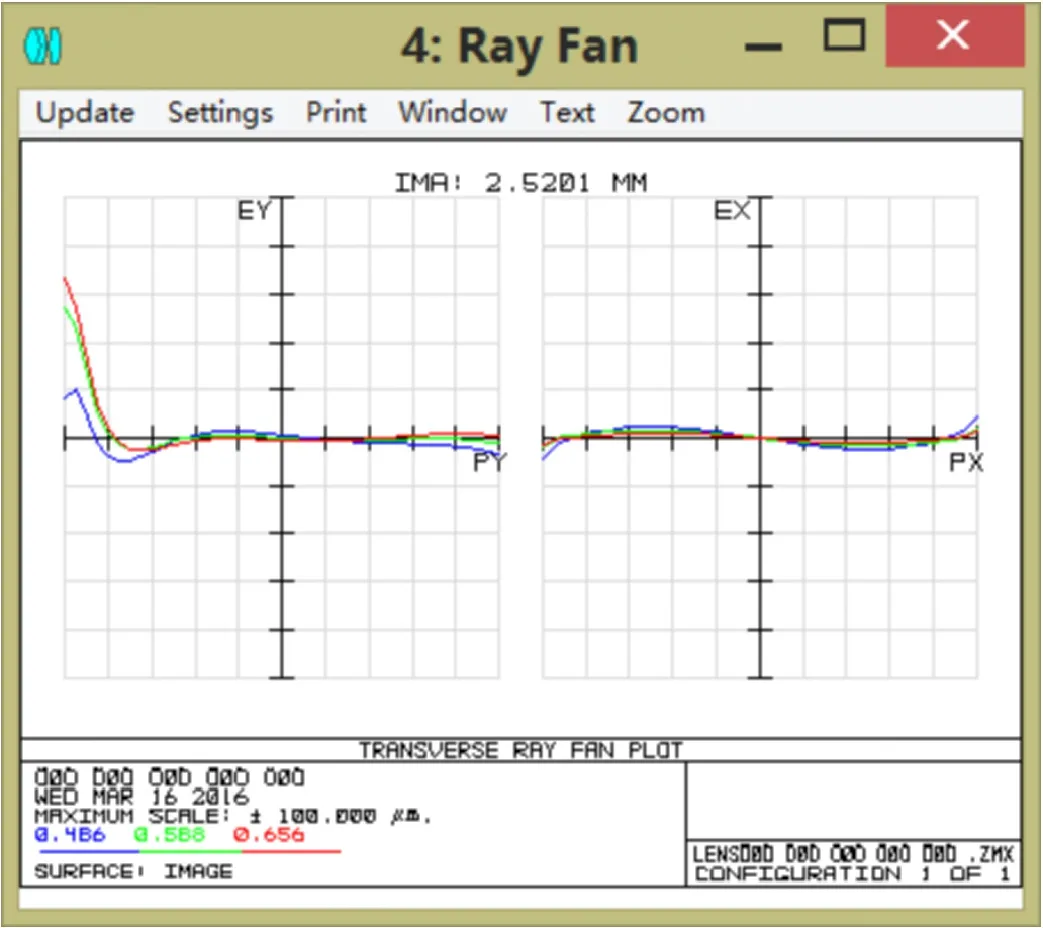
图7　光线扇形图

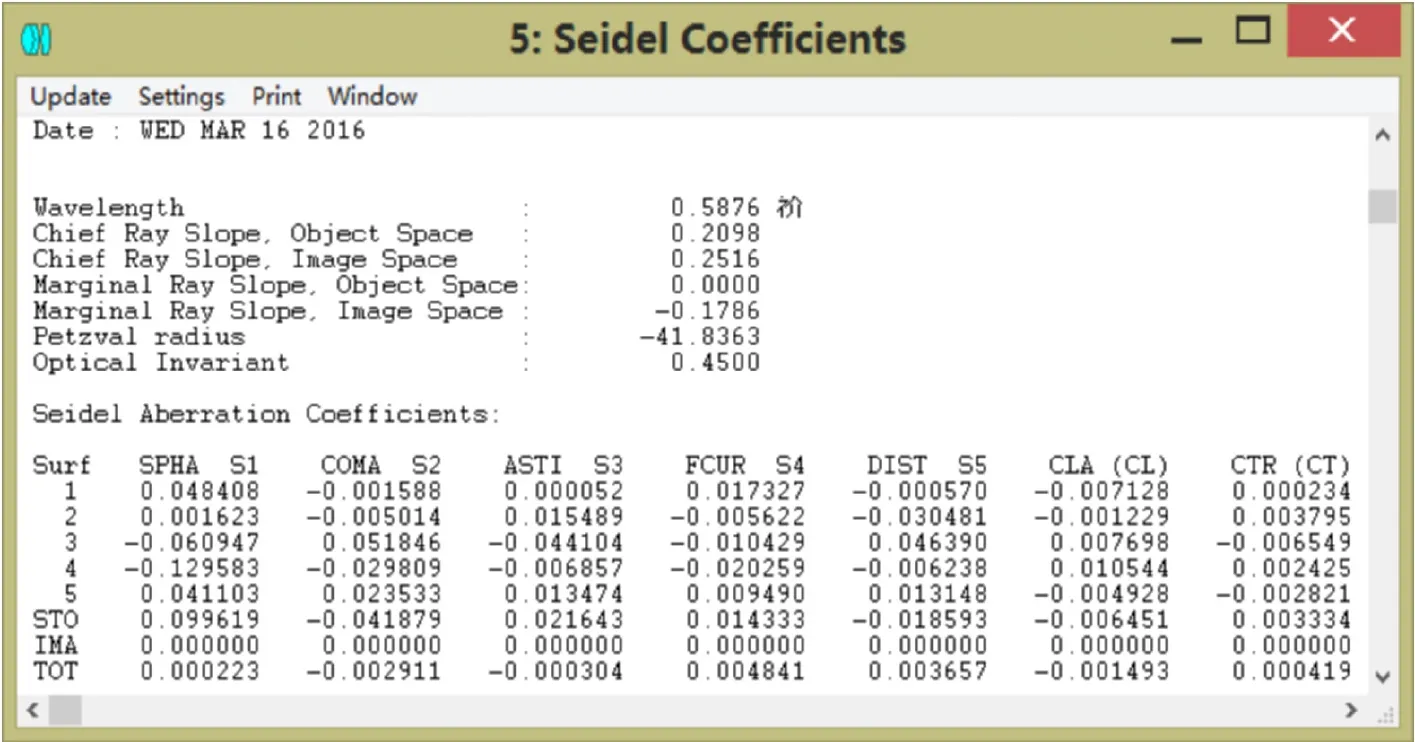
图8　赛德尔系数图