应用于无线电能传输的Litz线平面矩形螺旋线圈高频电阻计算

邓其军　刘姜涛　陈　诚　蒋　燕　周　洪

(1.武汉大学自动化系　武汉　430072 2.湖北第二师范学院物理与机电工程学院　武汉　430205)

应用于无线电能传输的Litz线平面矩形螺旋线圈高频电阻计算

邓其军1刘姜涛2陈诚1蒋燕1周洪1

(1.武汉大学自动化系武汉430072 2.湖北第二师范学院物理与机电工程学院武汉430205)

摘要在外部磁场的影响下，导线中的高频电流呈不均匀分布，致使其导电面积远小于横截面积，从而引起额外的电阻，称之为高频电阻。高频电阻中的感生电阻与磁场的平方呈正比。应用毕奥-萨伐定律对Litz线平面矩形螺旋线圈中的磁场进行分析，以计算线圈中的高频电阻，进而分析其最大品质因数及最优运行频率。对几个线圈原型的测量表明，该分析方法较好地预测了线圈在不同频率下的电阻及最优运行频率。使用两个外边长460 mm×208 mm、内边长312 mm×64 mm的矩形线圈所制作的无线能量传输系统，距离500 mm时，在稍低于预测的最优频率时获得的最大DC-DC效率为58.7%，接收端功率为50 W。

关键词：邻近效应高频电阻毕奥-萨伐定律Litz线无线电能传输

0引言

在无线电能传输等高频应用领域，电感线圈常使用Litz线来绕制以降低趋肤效应[1-4]。对于无线电能传输系统而言，更高的品质因数，意味着更高的效率[5-7]。线圈的品质因数与运行频率呈正比，与电阻呈反比。但过高的运行频率会加剧导线中的紊流并引起高频电阻的上升，反而会降低线圈的品质因数。为此，需要对线圈电阻与频率的关系进行分析，以寻求最大品质因数下最优的运行频率。

趋肤效应和邻近效应是引起线圈高频电阻的主要原因。前者表现为高频电流只在导线的表面通过，而导线中心的电流密度很小；后者表现为导线内的电流受外部磁场的影响而呈不均匀分布。相应的电阻称为导通电阻和感生电阻。对于单根的圆导体，通常使用贝塞尔函数来表达其高频条件下的电流密度，进而计算高频电阻[1-3]。导通电阻与导线的直径和频率有关，本文只引用现有结论进行计算；而感生电阻除与导线的直径和频率有关外，还与所处的磁场强度的平方呈正比[1-4，8-14]。因此，感生电阻的计算转换为对导线所处位置磁场强度的计算。

平面矩形螺旋线圈占用空间较小，易于制造，且具有比相同最大尺寸的圆螺旋线圈(矩形线圈的最大边长等于圆螺旋线圈的最大直径)更大的电感。因此，本文以平面矩形螺旋线圈为例来计算高频电阻。

对于平面圆螺旋线圈的电磁场，文献[2]使用麦克斯韦方程组计算。该方法比较复杂，且只对圆线圈有效，无法应用于矩形线圈。文献[3]使用有限元仿真的方法计算电磁场，但只考虑了Litz线上下两个表面的电磁场，精度不够高。上述两种方法都认为同一圈圆形线匝沿导线轴线方向的磁场是不变的，因此每圈只需计算一次。但由于矩形线圈的不对称性，沿导线轴向方向不同位置的磁场各不相同，使用有限元方法计算的工作量巨大。文献[14]使用迭代方法计算外部磁场以计算高频电阻，但其只考虑了Litz线束内部内绝缘导线间的邻近效应，而忽略了线匝间邻近效应。

本文提出使用毕奥-萨伐定律对Litz线平面矩形螺旋线圈的磁场进行分析，进而计算其感生电阻。一个3圈的平面矩形螺旋线圈的尺寸定义如图1a所示。在忽略边缘效应的条件下，可简化为图1b所示。后续分析均基于图1b。

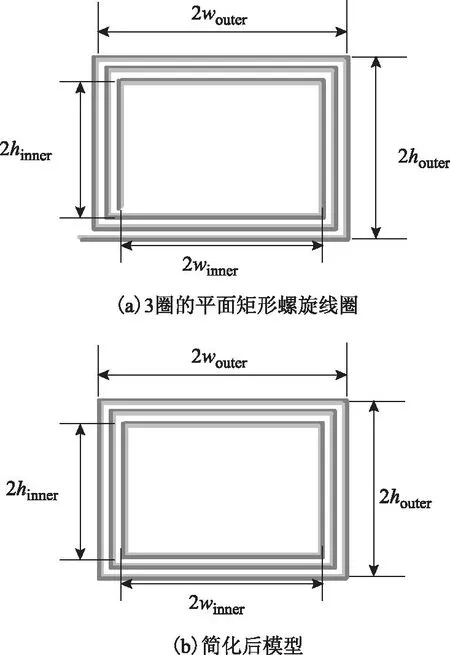
图1　平面矩形螺旋线圈及其简化模型Fig.1　Planar rectangular solenoid coiland its simplified model

1高频电阻的计算

高频电阻可表示为[1-3]

RAC=Rcond+Rindu

(1)

式中，Rcond及Rindu分别为导通电阻及感生电阻，Ω。

1.1导通电阻的计算

导通电阻Rcond为[1-3]

(2)

式中，2wj、2hj分别为第j圈(1≤j≤Nt，Nt为线圈的总圈数)的宽度和高度，m；Rcond-u，l为单位长度Litz线的导通电阻，Ω/m；ξ为与趋肤深度δ相关的量，m，如式(3)和式(4)所示；Φcond(ξr0)如式(5)所示；n0、r0分别为组成Litz线的单股外绝缘细铜线的股数和半径，m；σ为电导率，对于铜σ约为5.8×10-7S/m。

(3)

式中，μ0为自由空间磁导率，μ0= 4π×10-7H/m；μr为材料的相对磁导率，对于铜μr=1；ω为角频率，rad/s。

(4)

(5)

式中，ber、bei′、bei、ber′为开尔文函数。

1.2感生电阻的计算

Litz线圈中单位长度的单股圆截面细线的感生电阻为[1]

(6)

式中，H为当线圈中通过1A幅值的正弦电流(即每股细绝缘线中流过1/n0A)时产生的磁场强度的幅值，A/m。

(7)

式中，ber2为开尔文函数。

在理想情况下，一定长度的细铜线经过了Litz线横截面的所有位置，故可认为每股线的磁场强度、电流和消耗的功率都相同[1]。其中，式(6)中的平方磁场强度可用横截面处按面积平均的平方磁场来代替。

Litz线中的每股细铜导线，沿其轴向位置各处的磁场并不相同。因此，需要沿轴向长度对式(6)求定积分的方法计算每股导线的感生电阻。同时考虑到n0股线的电阻是单根线的1/n0，从而整根Litz线的感生电阻为

(8)

对于半径为rb的Litz线，轴向位置为y处的横截面上各点的磁场强度并不相等。但根据前述的每股外绝缘细铜线经过了Litz横截面的所有位置的假设，可计算其按面积平均的平方磁场强度为

(9)

(10)

1.3感生电阻的电流不均匀系数

理论上，组成Litz线的每股外绝缘细导线的电流相同。但实际中，当细导线的股数较多时，每股线的电流逐渐变得不相同，并导致比1.2节所述的更大的紊流及感生电阻。参考文献[15，16]，认为这是因为接头处的趋肤效应导致在接头表面的细铜线电流密度比接头内部的大，但仍可认为感生电阻与磁场强度呈正比。

另外，线圈附近的材料，特别是线圈的支撑托盘的制作材料，也对其感生电阻有很大影响。支撑托盘使用相对磁导率较大的材料制作，比使用磁导率小的材料制作时，线圈具有更大的高频电阻。

上述因素对感生电阻的影响可以用一个感生电阻的电流不均匀系数kindu来表示。从而式(8)可修改为

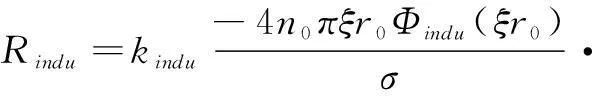
(11)

对于不同股数及环境的Litz线，可以通过实验的方法来测定该系数。

2磁场强度分析

在分析第j圈(1 ≤j≤Nt)的边AB处的磁场时，将图1b转换成图2(每圈的电流方向都相同)，并作如下假设：

1)每圈都分成4条边，即两个宽度的边(AB、CD)和两个高度的边(DA、BC)来分别考虑。

2)AB边垂直于轴向，有横截面积，电流均匀分布于该横截面，需要分别计算其横截面上各点的磁场。

3)第j圈的其余3条边及其他圈所有的边是没有横截面积的，所有的电流都集中于中心线，即视为所谓的“细丝电流”。

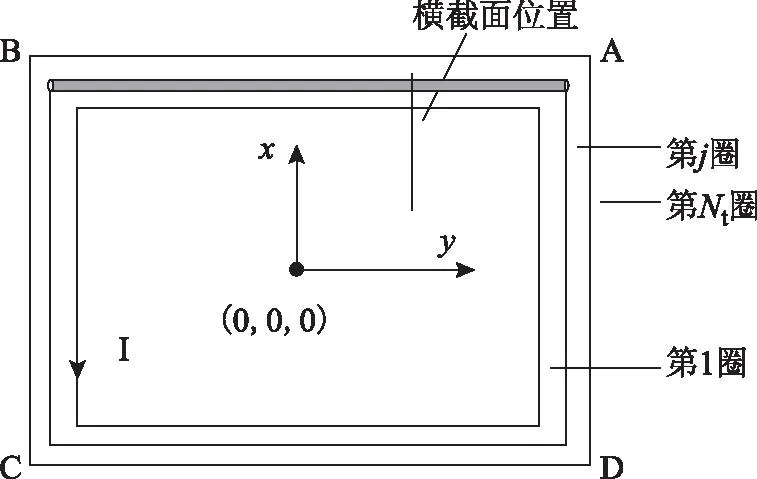
图2　用于计算第j圈磁场时的矩形线圈模型Fig.2　Coil model for magnetic field calculation in the jthturn

过j圈上部轴向位置y处作一横截面，其左视图如图3所示，其中Hi(AB)_j(y,r,φ)是第i圈的边AB在单位幅值电流条件下对第j圈在y处的横截面上的点P(r，φ)产生的磁场。

参考文献[2，3]使用麦克斯韦方程组计算电磁场，但只能应用于圆线圈而不能应用于矩形线圈。为此，本文使用毕奥-萨伐定律来分析各条边在P点产生的磁场，然后将该磁场矢量按3个方向累加得到P点各方向的磁场分量。

将第i圈的边AB视为长直导线，当AB中流过单位幅值的正弦电流时，在P点产生的磁场强度(如图4所示，A/m)可用毕奥-萨伐定律计算，如式(12)所示。

(12)

式中，θ1、θ2分别为直线AP、BP与细丝电流AB的夹角，rad；ρ为P到AB的距离，m。

(13)

式中，r、φ如图3所示。

图4　用于计算长直导线AB在P点的磁场强度Fig.4　Diagram for field calculation of P due to line AB

将Hi(AB)_j(l1,r,φ)分解到x、y、z三个方向，得到

(14)

集成式(12)～式(14)得到

(15)

特别地，当i=j时，第j圈内部流过AB的电流在其自身引起的磁场及3个分量可表示为[2，3]

(16)

同理，可得到第i圈的另外3条边BC、CD、DA流过单位幅值电流时在P点产生的磁场强度在3个方向的分量分别为式(17)～式(19)。

(17)

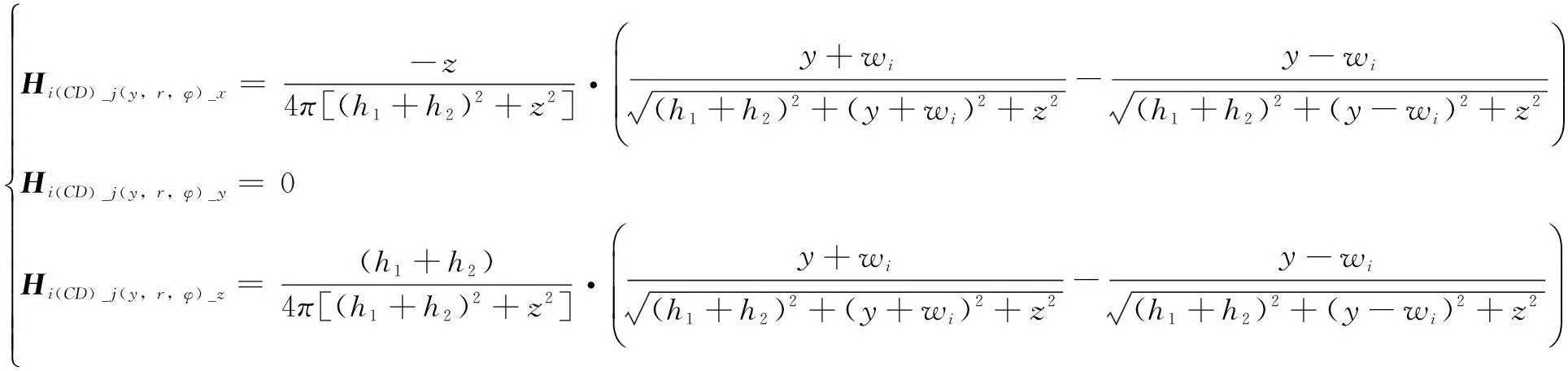
3.1.2 穿刺部位的暴露 锁骨下静脉穿刺患者取仰卧位，头偏向对侧，肩放平。肩下垫一棉垫，使两肩后展，锁骨略向前，充分暴露穿刺部位。颈内静脉穿刺患者采用15～20°头低足高仰卧位，两肩之间垫一薄枕，头后仰并转向对侧。采用头低位可使静脉充分充盈，静脉内压增高，容易穿刺，亦可避免产生脑内静脉空气栓塞。

(18)

(19)

据此，可计算所有的边在P点产生的磁场分解到3个方向的分量分别为

(20)

将式(20)代入式(10)，即可得到P点的平方磁场。

3线圈最大品质因数

对于无线电能传输系统而言，线圈的品质因数定义为

(21)

式中，ω、L分别为线圈中正弦波电流的角频率和电感。通常情况下，线圈电感L随频率变化很小可以忽略不计，则通过求解

(22)

即可得到最大品质因数Qmax及相应的最优角频率ωopti。但由式(1)、式(2)、式(5)～式(7)可知，分析电阻时Φindu(ξr0)及Φcond(ξr0)的计算公式比较复杂，难以求导。为此，需要对其进行简化。当ξr0<1时，即

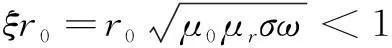
(23)

式(5)和式(7)中所有Kelvin函数的高次项均可忽略不计，从而得到

(24)

集成式(1)、式(2)、式(8)和式(24)，可将式(21)简化为

(25)

将式(25)代入式(22)并求解，可得最优角频率及最大品质因数分别为

(26)

4实验验证

为验证上述高频电阻计算方法，制造了4种矩形平面螺旋线圈，并对其高频电阻进行测量。4种线圈的参数如表1所示。线圈Ⅰ和Ⅳ所使用的Litz线为1类圆线(Round Type 1)；Ⅱ和Ⅲ为2类圆线(Round Type 2)，绕制结构为5×5×42[17]。其中线圈Ⅰ、Ⅱ、Ⅳ布置在透明胶带上面，没有使用托盘支撑；线圈Ⅲ使用5 mm厚度的拼接木板作为托盘，并使用2 mm边长的正方形截面细木条制作走线槽以保证圈与圈之间的间距均匀。线圈Ⅲ如图5所示。

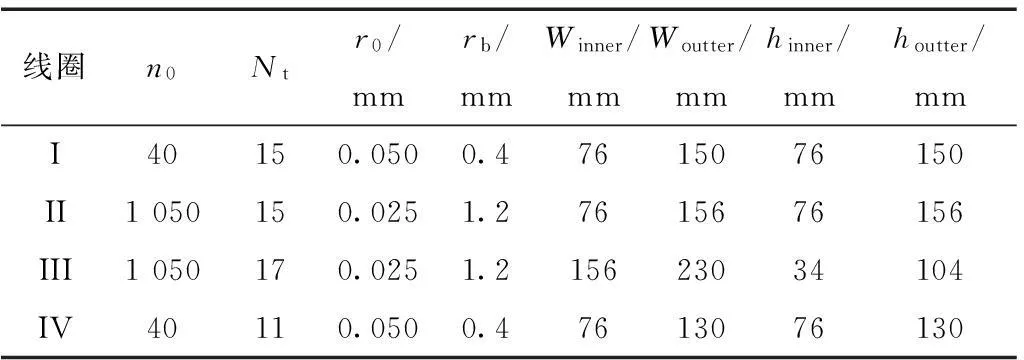
表1　线圈参数

图5　矩形平面螺旋线圈Fig.5　A planar rectangular solenoid coil

4.1磁场强度仿真计算

根据上述方法，使用Matlab编写了磁场及电阻计算的仿真代码。图6是根据式(9)计算在y=0(即宽边中点)位置时，线圈Ⅱ各圈的平均平方磁场强度。同时，处于内边缘(如第1圈)及外边缘(如第15圈)的圈的平方磁场较大，而处于中间位置(如第10圈左右)的圈的平方磁场较小。这是因为两边的圈在中间圈附近所产生的电磁场能够相互抵消一部分。例如，图2中第1圈的AB边及第Nt圈的AB边在第j圈的AB边沿轴线处产生的电磁场方向分别为向下(z轴的负方向)、向上(z轴的正方向)，刚好能够抵消一部分。

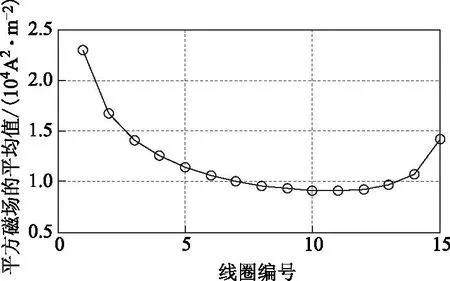
图6　线圈Ⅱ边长中点的平方磁场强度Fig.6　Squared field strength at center of width of coil Ⅱ

4.2感生电阻的电流不均匀系数的测量与计算

线圈放在不同位置，所测得的高频电阻差异很大。例如，将线圈Ⅱ分别放在纸盒子上和高密度板制作的桌面上，在1 MHz时测得的电阻分别为615 mΩ和861 mΩ(本文的电阻测量均使用一台Agilent E4980A精密阻抗测量仪进行)。考虑几种线圈的实际使用场景，测量电阻时，线圈Ⅰ、Ⅱ和Ⅳ放置于纸箱上来进行；线圈Ⅲ则通过木支架竖直放置于桌面上；另将线圈Ⅱ放置于高密度板桌面上作对比测量。

通过测量线圈在某个频率的电阻，并减去根据式(2)计算得到的导通电阻，即得到其实际的感生电阻。该感生电阻除以式(8)计算得到的值，即可求得感生电阻的电流不均匀系数kindu。在较低频率(小于100 kHz)时，导线的趋肤深度远大于表1所示的Litz线的半径，从而其高频电阻基本上等于直流电阻，即其感生电阻分量接近0。因此，为减小误差，在关注的频率范围内(本文为1 kHz～1 MHz)，选取了两个较高的频率点，即300 kHz和700 kHz来测量线圈的电阻以计算kindu。对于线圈Ⅰ，在这两个频率时测量得到的电阻分别为850 mΩ、1258 mΩ；依式(2)计算得到的导通电阻分别为736 mΩ、738 mΩ；依式(8)计算得到的感生电阻分别为72 mΩ、384 mΩ，从而计算其平均的感生电阻系数为

(27)

同理可对线圈Ⅱ、Ⅲ、Ⅳ及线圈Ⅱ置于高密板桌面上进行测量，并计算得到其感生电阻系数分别为2.30、3.36、1.38、3.10、。线圈Ⅱ的kindu比线圈Ⅰ大，是因为其Litz线的股数较多；而线圈Ⅲ比线圈Ⅱ的kindu大，是因为拼接木板、走线槽及使用了木头胶水以固定细木条等因素的影响。线圈Ⅱ放置于高密度板桌面上比放置于纸箱上时的kindu大一些，是因为桌面PVC贴纸造成线圈寄生电容增大的影响。比较线圈Ⅰ和线圈Ⅳ的测量结果可知，在相同的使用环境下，使用相同规格的Litz线制作的不同尺寸的线圈，其感生电阻不均匀系数非常接近。

4.3电阻及品质因数的测量

当Litz线内部的绝缘细铜导线半径r0=0.05 mm时，ω为

(28)

即角频率低于5.5 MHz时，式(24)成立。同理可计算r0=0.025 mm时，式(24)成立的条件是角频率低于22 MHz。仍使用Agilent E4980A精密阻抗测量仪，测量线圈从1 kHz～1 MHz(每隔1 dB测量一次)的电阻及品质因数。电阻实测值及仿真预测值按对数坐标系显示于图7，品质因数实测值及仿真预测值显示于图8(4个线圈的电感在1 kHz时的实测值分别为77 μH、78 μH、107 μH、44 μH)。

由图7可见，预测电阻值与实测电阻值具有很高的吻合度。就最大品质因数而言，依式(26)计算得到前3个线圈的最优频率分别为891 kHz、541 kHz、374 kHz；对应的最大品质因数分别为272、1 132、844。实测的最优频率分别为1 MHz、600 kHz、400 kHz；对应的最大品质因数分别为285、1 170、899。可见线圈Ⅰ的实测最优频率稍微超出了式(24)限定的范围，从而使用式(26)预测其最大品质因数和最优角频率会有一定误差；而线圈Ⅱ和Ⅲ的最优角频率远低于式(24)限定的范围，故预测的最优频率和最大品质因数与实测值较接近。

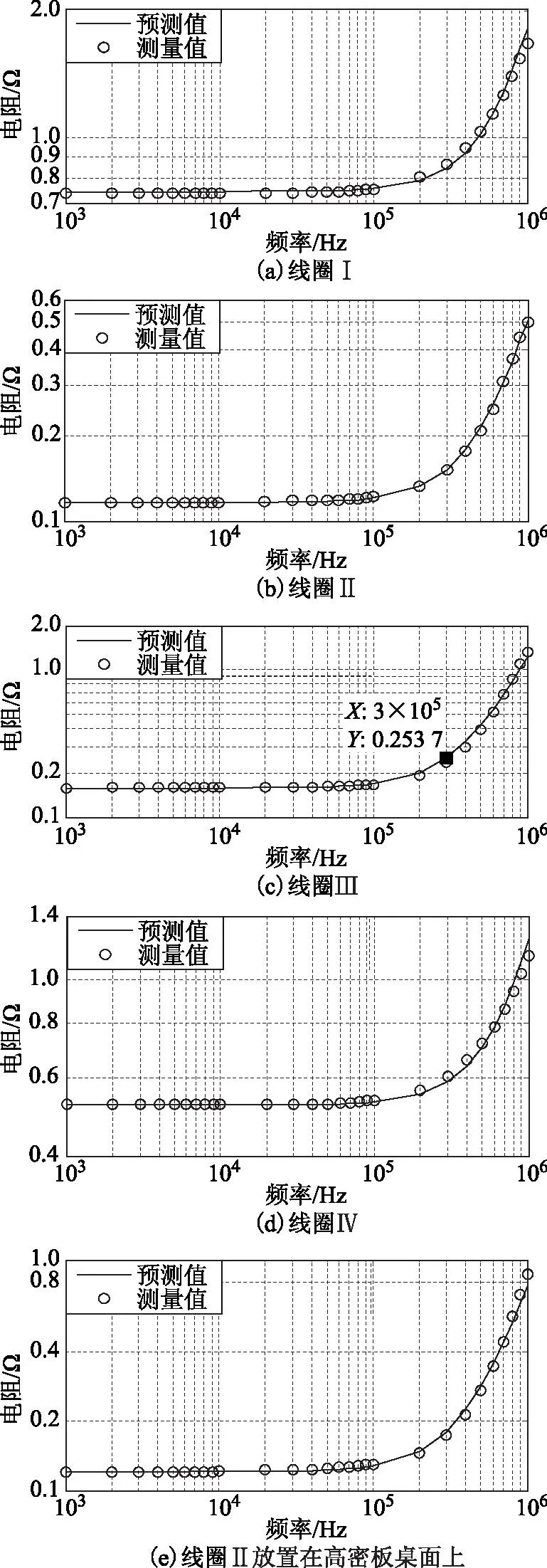
图7　线圈的实测电阻与预测电阻 Fig.7　Measuring resistance and predicted one for coils

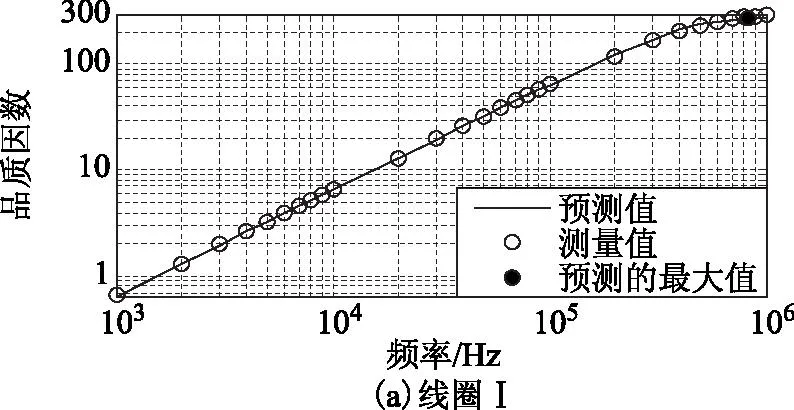
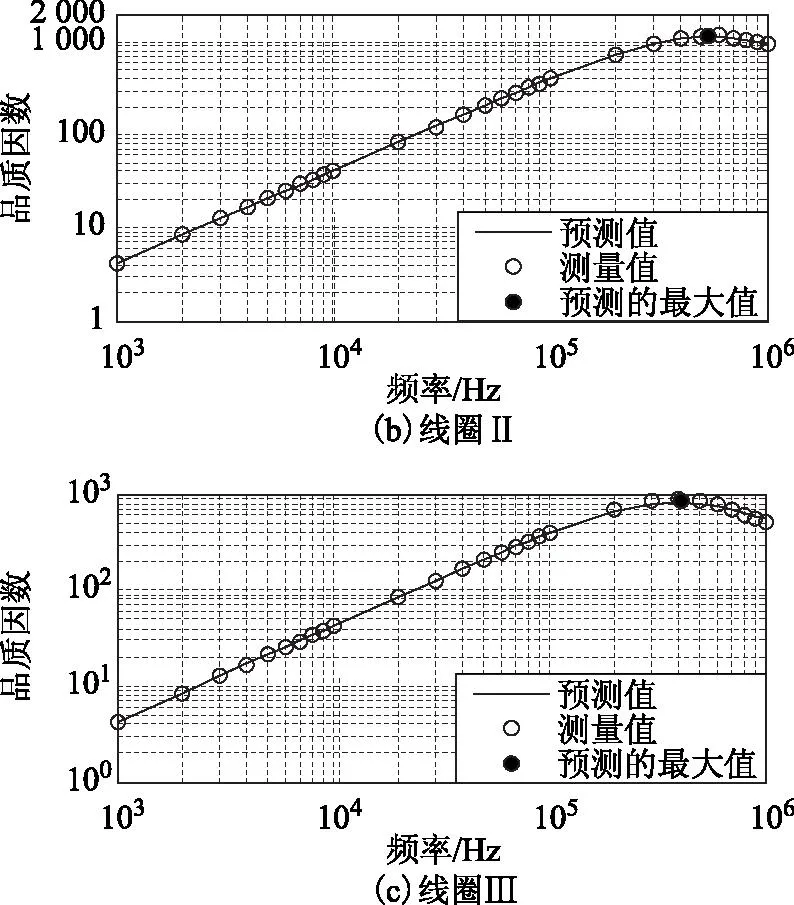
图8　线圈的实测品质因数与预测品质因数 Fig.8　Measuring quality factor and predicted one for

图7b和图7d的比较表明，对于相同的线圈，当使用环境不同时(如线圈托盘或支架材料不同)，其电流不均匀系数也不同，但仍能根据式(1)及式(11)较准确地预测其不同频率下的电阻。

4.4线圈寄生电容对电阻测量的影响

文献[18]表明，真实的线圈是一个包括有寄生电容的RLC电路。当使用LCR仪器测量时，仪器显示的Rs值其实是该RLC电路的阻抗的实部，且真实电阻R0与测量值r关系为[18]

(29)

式中，ω0和C分别为线圈的自谐振频率和寄生电容。当运行频率远小于谐振频率时，寄生电容对测量结果的影响可以忽略不计。寄生电感通过测量线圈的自谐振频率(用LCR阻抗分析器测量线圈的电感值，当该值由正值转为负值时的频率)及线圈在低频时的电感值来计算。使用MicroTest 6620型阻抗分析仪，测得表1所示4个线圈及线圈Ⅱ放置于高密度板桌面时的自谐振频率分别为7.69 MHz、7.70 MHz、5.52 MHz、8.96 MHz、6.46 MHz。由于已测得4个线圈在低频时的电感分别为77 μH、78 μH、107 μH、44 μH，可根据式(29)计算其寄生电容分别为5.6 pF、5.5 pF、7.8 pF、7.2 pF、7.8 pF。由于寄生电容值很小，式(29)中计算r/R0时，其分母的第二项可忽略不计。最终对于4个线圈的5种使用场景，在1 MHz时，用式(29)计算r/R0的值分别为1.03、1.03、1.07、1.03、1.05。这表明，寄生电容对电阻测量值的影响较小。因此，将Agilent E4980A测得的值作为其真实电阻值是可行的。

4.5无线电能传输系统原型样机

在发送端和接收端，分别使用一个相同尺寸的线圈(规格如表1中的的线圈Ⅲ)作为能量发送与接收线圈，两个线圈距离500 mm。整个系统如图9所示。发射端的逆变器采用D类全桥方式，由4个BSB056N10NN3型号的MOSFET组成，占空比为0.45。该型号MOSFET的导通电阻为5.6 mΩ，其损耗与线圈相比可忽略不计。

图9　无线电能传输系统原型机Fig.9　Prototype of the wireless power transfer system

通过调整串连谐振电容的容值来调节系统的谐振频率，从而比较系统在不同运行频率下的效率。同时，使用Agilent E4980A测量发射端与接收端的谐振频率，并使用小容量的电容对电容值进行微调，以保证两端有相同的谐振频率。

接收端经全桥整流器后，并联5个额定电压12 V、额定功率10 W的灯泡作为负载。对于不同的运行频率，均通过调整逆变器输入直流电压使5个并联的灯泡的电压达到12 V。

系统在7个典型运行频率下的DC-DC效率(即灯泡的功率与输入逆变器的功率之比)测量结果如表2所示。由表2可见，系统在频率305 kHz时，实测的最高效率为58.7%。该频率比预测的最大效率时的频率(374 kHz)要低一些。这是因为，对于本无线电能传输系统所使用的S-S型(串-串型)结构，在电感一定的情况下，降低运行频率能够增大串连电容。而容值较大的电容的寄生电阻较小，从而有利于系统效率的提升。因此，实际的运行频率比预测的最大品质因数对应的频率小一些。

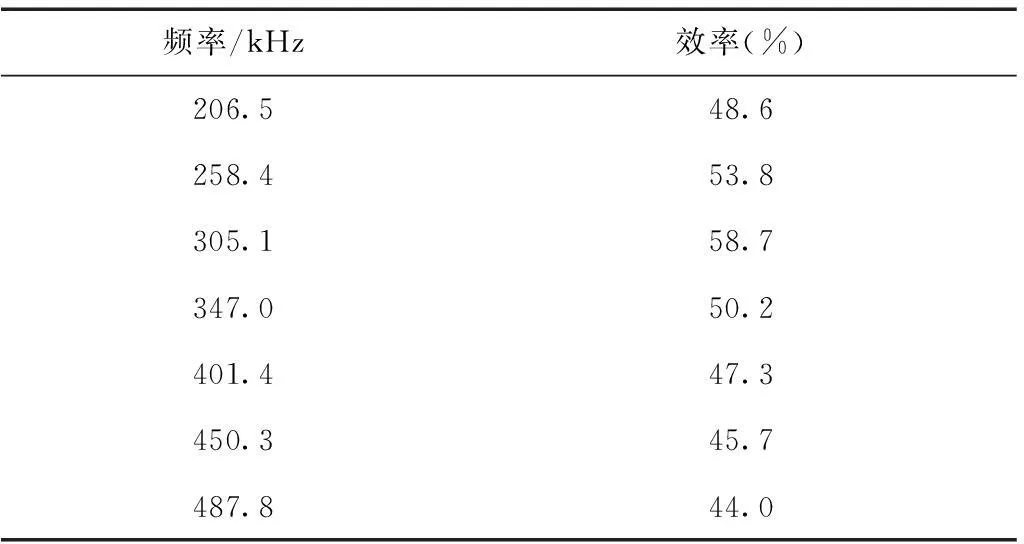
表2　系统在不同串联谐振电容(运行频率)下的效率

5结论

应用毕奥-萨伐定律对Litz线平面矩形螺旋线圈中的磁场进行分析，并结合半理论半实验方法测量感生电阻电流不均匀系数，进而对线圈的感生电阻及总电阻进行计算，在1 kHz～1 MHz频率范围内，所得预测值与实测值具有较高的吻合度。该方法能够进一步预测出线圈的最大品质因数及相应的最优运行频率。当无线电能传输系统在稍低于该频率下运行时，能够获得最大的系统效率，从而为确定无线电能传输系统最佳运行频率提供参考。另外，相同规格的Litz线所制作的不同尺寸的线圈，在相同的使用环境下，具有相同的感生电阻电流不均匀系数。因此能够使用本方法来预测相同Litz线制作的不同尺寸线圈的高频电阻及其品质因数，从而为线圈的设计提供依据。

[1]Carretero C，Acero J，Alonso R.TM-TE decomposition of power losses in multi-stranded Litz-wires used in electronic devices[J].Progress in Electromagnetics Research，2012，123(1)：83-103.

[2]Acero J，Alonso R，Burdio J M，et al.Frequency-dependent resistance in Litz-wire planar windings for domestic induction heating appliances[J].IEEE Transactions on Power Electronics，2006，21(4)：856-866.

[3]Acero J，Hernandez P J，Burdio J M，et al.Simple resistance calculation in Litz-wire planar windings for induction cooking appliances[J].IEEE Transactions on Magnetics，2005，41(4)：1280-1288.

[4]Nan X，Sullivan C R.An equivalent complex permeability model for Litz-wire windings[J].IEEE Transactions on Industry Applications，2009，45(2)：854-860.

[5]石新智，祁昶，屈美玲，等.基于磁共振的无线能量传输系统接收模块参数研究[J]，电工技术学报，2014，29(2)：204-211.

Shi Xinzhi，Qi Chang，Qu Meiling，et al.Receiver parameters analysis of wireless energy transfer system based on magnetic resonance[J].Transactions of China Electrotechnical Society，2014，29(2)：204-211.

[6]朱春波，于春来，毛银花，等.磁共振无线能量传输系统损耗分析[J].电工技术学报，2012，27(4)：13-17.

Zhu Chunbo，Yu Chunlai，Mao Yinhua，et al.Analysis of the loss of magnetic resonant wireless power transfer[J].Transactions of China Electrotechnical Society，2012，27(4)：13-17.

[7]王智慧，吕潇，孙跃，等.谐振式无线电能传输系统损耗模型[J].电工技术学报，2014，29(9)：17-21.

Wang Zhihui，Lü Xiao，Sun Yue，et al.Modeling of power loss in resonant wireless power transfer system[J].Transactions of China Electrotechnical Society，2014，29(9)：17-21.

[8]Nan X，Sullivan C R.Simplified high-accuracy calculation of eddy-current loss in round-wire windings[C]//IEEE Power Electron Special conference(PESC)，Aachen，Germany，2004：873-879.

[9]Pantic Z，Lukic S.Computationally efficient，generalized expressions for the proximity-effect in multi-layer，multi-turn tubular coils for wireless power transfer systems[J].IEEE Transactions on Magnetics，2013，49(11)：5404-5416.

[10]Wojda R P，Kazimierczuk M K.winding resistance of Litz-wire and multi-strand inductors[J].IET Power Electronics，2012，5(2)：257-268.

[11]Murthy-Bellur D，Kondrath N，Kazimierczuk M K.Transformer winding loss caused by skin and proximity effects including harmonics in PWM DC-DC flyback converter for continuous conductive mode[J].IET Power Electronics，2011，4(4)：363-373.

[12]Dowell P L.Effects of eddy currents in transformer windings[J].Proceedings of the Institution of Electrical Engineers，1966，13(8)：1387-1394.

[13]Kazimierczuk M K.Skin Effect[M]//High Frequency Magnetic Components.Chichester：John Wiley &Sons Ltd.，2009.

[14]黄晓生，陈为.线圈高频损耗解析算法改进及在无线电能传输磁系统设计的应用[J].电工技术学报，2015，30(8)：62-70.

Huang Xiaosheng，Chen Wei.Improved analytical calculation model of high-frequency coil losses and its usage in WPT magnetic system[J].Transactions of China Electrotechnical Society，2015，30(8)：62-70.

[15]Rossmanith H，Doebroenti M，Albach M，et al.Measurement and characterization of high frequency losses in non-ideal Litz wires[J].IEEE Transactions on Power Electronics，2011，26(11)：3386-3394.

[16]Rosskopf A，Bar E，Joffe C.Influence of inner skin-and proximity effects on conduction in Litz wires[J].IEEE Transactions on Power Electronics，2006，21(10)：5454-5461.

[17]New England Wire Company.Product selection guide[EB/OL].https：//www.newenglandwire.com/newt-catalog.pdf.2016-03-28.

[18]Kazimierczuk M K.Self-Capacitance[M]//High Frequency Magnetic Components.2nd ed.Chichester：John Wiley &Sons Ltd.，2014.

High Frequency Resistance in Litz-Wire Planar Rectangular Solenoid Coils for Wireless Power Transfer

Deng Qijun1Liu Jiangtao2Chen Cheng1Jiang Yan1Zhou Hong1

(1.Department of AutomationWuhan UniversityWuhan430072China 2.School of Physics and Electrical EngineeringHubei University of EducationWuhan430205China)

AbstractThe high frequency current is un-uniform in the wire due to external magnetic field.As a result,the conductive area of the wire is far smaller than its cross-section,and the excess resistance,namely the frequency-dependent resistance,is induced.The high frequency resistance is proportional to the square of the magnetic field the wire exposed to.The paper employees the Biot-Savart law to analyze the magnetic field distribution of the planar rectangular solenoid coils for evaluating the frequency-dependent resistance.The maximum quality factor of the coil and the corresponding optimal operation frequency are derivate based on the analyses of the field and resistance.A few coils are manufactured and their high frequency resistances are measured.The measurements show that the proposed method predicts the resistance under various frequencies and the optimal operation frequency precisely.Two coils,whose outer and inner dimensions are 460 mm×208 mm and 312 mm×64 mm,are employed to build a wireless power transfer system.Under the frequency slightly lower than the predicted optimal one,the system obtains the maximum DC-DC efficiency of 58.7% and receives 50 watts power at the distance of 500 mm.

Keywords：Proximity-effect，high frequency，the Biot-Savart law，Liz-wire，wireless power transfer

收稿日期2015-04-19改稿日期2016-01-05

作者简介E-mail：dqj@whu.edu.cn(通信作者) E-mail：liu_jiangtao@whu.edu.cn

中图分类号：TM724

国家科技支撑计划资助项目(2013BAA01B01)。

邓其军男，1975年生，博士，副教授，研究方向为无线电能传输、谐振电力变换、电力信息化。

刘姜涛女，1979年生，博士，副教授，研究方向为无线电能传输、电力变压器有源降噪等。