基于FLAC3D的初始地应力场生成方法研究

张　军，严　俊，乔海娟，马超峰

(1．水利部农村电气化研究所，浙江　杭州　310012；2．水利部农村水电工程技术研究中心，浙江　杭州　310012；3．溧阳市水利局，江苏　溧阳　213300)

基于FLAC3D的初始地应力场生成方法研究

张军1，2，严俊1，2，乔海娟1，2，马超峰3

(1．水利部农村电气化研究所，浙江杭州310012；2．水利部农村水电工程技术研究中心，浙江杭州310012；3．溧阳市水利局，江苏溧阳213300)

摘要：介绍利用FLAC3D进行初始地应力场模拟分析中的几种方法，着重描述了生成构造应力场所采用的几种边界条件，借助这几种不同的方法分别对某水电站调压室初始地应力场进行模拟分析，并将其结果与实测值进行比较，对每一种方案的实际模拟效果进行分析，为后续的工程分析提供可靠依据。图8幅，表4个。

关键词：初始地应力场；FLAC3D；分析

1概述

初始地应力场是围岩稳定的重要影响因素之一，也是工程设计的重要初始条件之一，因此在计算中采取的初始应力场是否合理，将对工程的可靠性和安全性产生直接影响[1]。现阶段初始地应力场的模拟方法主要有位移反分析法和应力回归分析法，前者通过对大地构造变形的观测或工程施工中的位移监测对工程区域的应力场进行反演研究。后者依据对工程区域地应力场产生条件的规律性认识建立三维模型，以实测地应力值为基础，在模型边界上施加不同组合的荷载和约束，通过数值计算，使得计算值与实测值达到最优拟合，以求得工程区域初始地应力场，这种方法可以很好的模拟出构造应力场[1_2]。本文结合某水电站工程，基于岩土工程软件FLAC3D，采用现阶段地应力反演中常用的几种边界条件对初始地应力场进行了模拟分析，并将其结果与实测值进行比较分析。

2几种拟合方法的边界条件比较

初始应力场的形成分为岩体自重和地质构造力这两部分。自重应力场的模拟多采用在模型侧面及底面加位移约束，仅限制其法向位移(见图1)，计算其在自重作用下产生的应力场。构造应力场的模拟目前主要采用的方法有以下3种：一是在侧面分别施加水平方向三角形或梯形荷载来模拟水平方向构造作用力，对非加载侧面边界和底部边界加位移约束，限制其法向位移[3](见图2)。二是李仲奎、戴荣等人提出的快速应力边界法(见图3)，即在初始地应力场形成过程中，数值模型不设速度边界条件，仅在模型表面根据地应力场的分布情况施加应力边界条件并保持恒定[4]。三是在模型的底面及侧面加位移约束，限制其方向位移，借助fish语言对模型的每个单元逐个施加轴向应力，使模型达到初始平衡，再进行计算(见图4)。

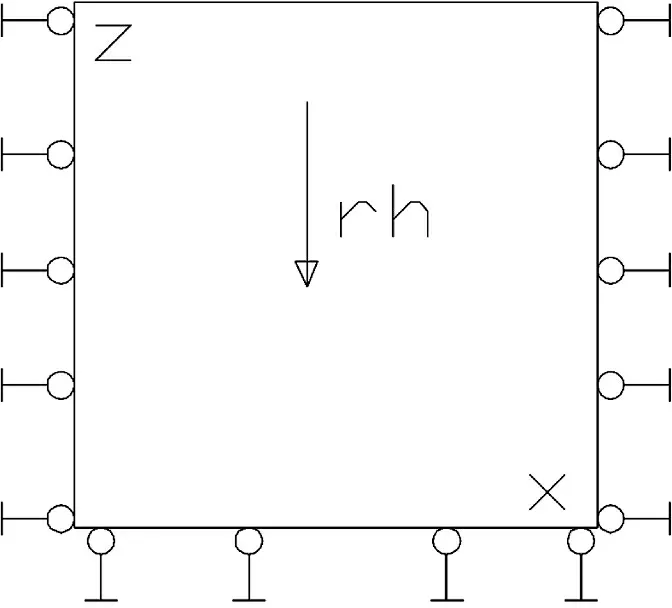
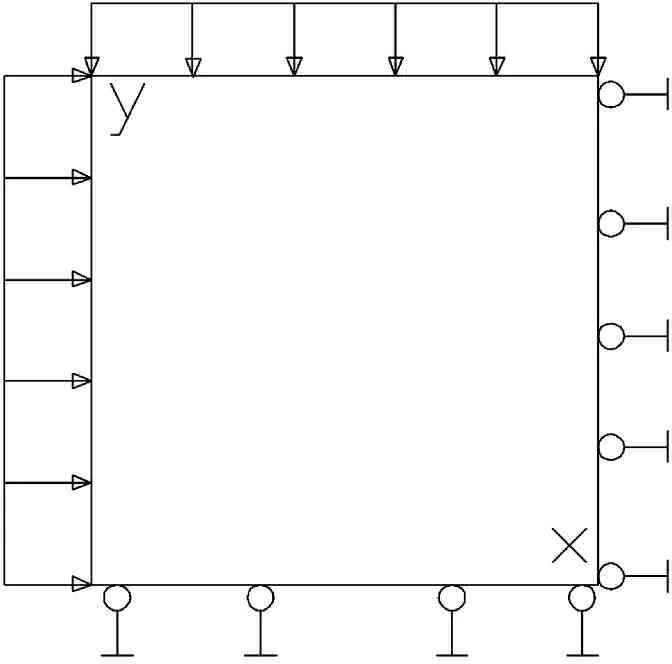
图1　自重应力场计算模式

图2　构造应力场计算模式1

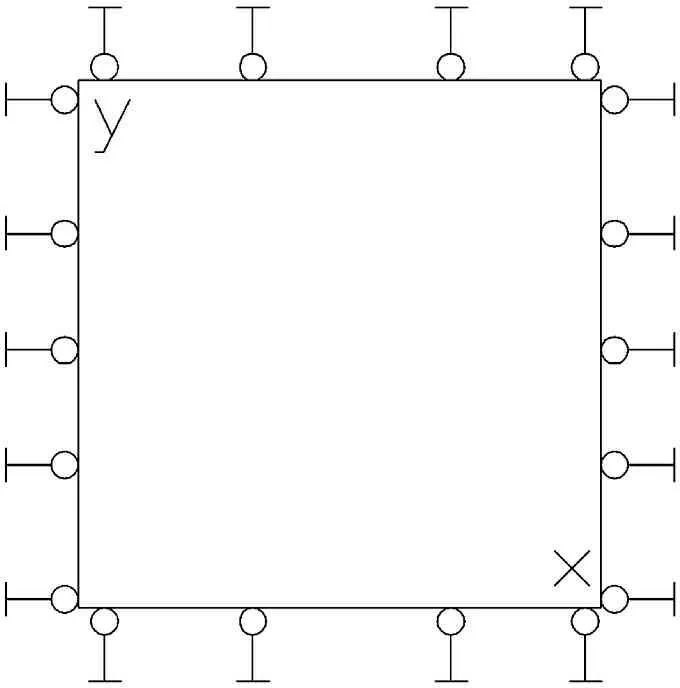
图3　构造应力场计算模式2

图4构造应力场计算模式3

3数值计算及结果比较

3.1计算模型及计算范围

根据计算要求和一般经验，对于地下洞室进行数值计算时模型范围选取的一般原则是：引水隧洞一般模型范围大于3～5倍的洞径，对于大型的地下洞室群要超出其影响范围建议不小于1.5倍洞室尺寸。据此本次计算模型的计算范围在X、Y、Z共3个方向分别取700 m×400 m×400 m，其中X轴为垂直水流方向指向左侧为正；Y轴为竖直方向向上为正；Z轴为顺水流方向指向下游为正(见图5)。所采用岩体物理力学参数如下所示(见表1)。

表1　岩体物理力学参数

图5 计算模型

3.2地应力实测结果分析

工程地质资料中给出了测点的3个主应力实测值，以及其水平投影与正北向的夹角α和仰角β(见表2)，而本次计算需要每个测点的6个应力分量，故还需转换，先由α、β求出斜截面的li、mi、ni，再由弹性力学公式和坐标轴旋转公式求得测点的6个应力分量。

li=cosβisinαi

mi=cosβicosαi

ni=sinβi

式中，li、mi、ni分别为σi对X,Y,Z轴的方向余弦。α为主应力在水平面上的投影方位角，以北为0，顺时针旋转。β为主应力的倾角，仰角为正。

表2　测点地应力实则值

根据每组实测主应力量值及方向余弦，再由下式将主应力转换成6个应力分量(见表3)：

τxy=l1m1σ1+l2m2σ2+l3m3σ3

τyz=m1n1σ1+m2n2σ2+m3n3σ3

τzx=n1l1σ1+n2l2σ2+n3l3σ3

表3　测点地应力转换值　MPa

3.3地应力反演方案及评价

因本工程地应力测点给得较少，本次计算以表3所求的应力分量，以地表应力为0，按线性分布，采用应力荷载调整法进行初始地应力场拟合。以前文所提及的生成构造应力场所采用的3种不同的边界条件作为3种方案，进行计算并比较分析。

方案一：计算区模型的右边界、前面边界为位移约束边界，约束水平方向的位移；左边界、后面边界为荷载约束边界；模型的底面也为位移约束边界，仅约束垂直方向的位移；模型的顶面按照施加分布力的方式来模拟由上部岩层产生的荷载。

方案二：计算区模型侧面及底面都以应力边界来约束模型，不施加位移边界条件。

方案三：计算区域模型的底面及侧面加位移约束，限制其法向方向位移，借助fish语言对模型的每个单元逐个施加水平正应力，使模型达到初始平衡，再进行计算。

3种方案下地应力场的分布情况如下所示(见图6～8，此处只列出第一主应力)，测点水平主应力实测值与拟合值对比如下所示(见表4)。

图6　方案一σ1

图7　方案二σ1

图8方案三σ1

4结论

由图5～8及表4可见，在实际测点不多或具体坐标不详的情况下，使用应力荷载调整法拟合的初始地应力场可以很好的反应出地应力水平，拟合值和实测值的误差在10%，完全可以满足计算的要求。

就本文所采用的3种方案，虽然各测点的拟合值和实测值都能满足误差要求，但就整个模型的地应力分布来说结论如下：

表4　地应力实测值与拟合值对比　MPa

方案一中对同一个侧面采用位移约束和应力边界约束这2种不同的方案，整个模型的地应力分布将会不同。

方案二所采用的快速应力边界法因为没有对其进行位移约束，导致整个模型的计算时间很长，尤其是单元比较多的大模型，耗时很长且模型顶部应力分布并不是很合理。

方案三借助fish语言对模型内各单元直接添加水平正应力，侧面及底面采用位移边界约束其法向位移，大大缩短了求解的时间且模型的应力分布符合规律。

参考文献：

[1]陈育民，徐鼎平. FLAC /FLAC3D基础与工程实例[M]. 北京：中国水利水电出版社，2008.

[2]郭怀志，马启超，薛玺成，等. 岩体初始应力场的分析方法[J]. 岩土工程学报，1983，5(3)：64_75.

[3]岳晓蕾.大岗山地应力反演与工程应用研究[D]. 济南：山东大学，2006．

[4]李仲奎，戴荣，姜逸明. FLAC3D分析中的初始应力场生成及在大型地下洞室群计算中的应用[J]. 岩土工程学报，2002，21(增2)：2387_2392.

■

责任编辑吴昊

收稿日期：2016-02-26

作者简介：张军(1986-)，男，工程师，主要从事水工结构设计工作。E_mail： jzhang@hrcshp.org