Alpha正态分布及其在环境污染中的应用

陈明明，马江洪，姬楠楠

(长安大学 a.经济与管理学院；b.理学院，陕西 西安 710064)

Alpha正态分布及其在环境污染中的应用

陈明明a，马江洪b，姬楠楠b

(长安大学 a.经济与管理学院；b.理学院，陕西 西安 710064)

摘要：目前，对实际数据的处理常采用一些对称分布，如正态分布和t分布等，而这种对称分布所给出的结果往往并不能令人满意。偏分布常用来处理有偏重尾数据，基于传统正态分布，提出一种处理偏态和重尾数据的alpha正态分布，并研究其参数估计方法及基本性质。将所提分布应用于环境污染数据，通过拟合检验alpha正态分布给出了很好的结果。

关键词：偏正态分布；alpha正态分布；MLE估计；环境污染

一、引 言

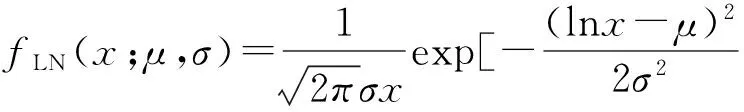
偏正态分布由Azzalini于1985年提出，由正态分布中引入非对称参数所得，偏正态分布作为正态分布的一种扩展，被广泛应用于建模不同的有偏重尾数据集中[9]。我们称随机变量X服从一元偏正态分布，若其密度函数为Ø(x;α)=2φ(x)Φ(αx),x,α∈R,记为X～SN(α)，其中φ(x)是标准正态分布的密度函数，Φ(x)是标准正态分布的分布函数，α是用来控制偏度的形状参数。当α=0时，就简化为正态分布；当α=1时它代表了两个独立标准正态变量最大值的分布。

由于此分布包含原正态分布，所以也有一些与原对称分布相同的性质，因此能很好地应用于有偏数据拟合中。Henze进一步研究了偏正态分布的概率表达式并推导出了此分布的奇数阶矩[10]；且Azzalini等将一元偏正态分布推广到了多元的情形[11-12]；随后Huang等给出了基于一个对称分布通过引入一个偏态函数来构建偏对称分布的一般公式[13]；陈明明等提出Levy偏稳定分布的性质等问题[14]。

目前，关于环境污染数据中大多应用了我们所熟知的对数正态分布，很少有文献将偏分布应用其中，本文在大量处理偏态数据分布的基础上[15]，提出了一种基于传统正态分布的alpha正态分布，并研究此分布的参数估计及相关的统计性质，最后将其应用于实际数据集中，同时通过比较正态分布、偏正态分布、对数正态分布及alpha正态分布，得出本文所提模型的有效性。

二、Alpha正态分布

定义1若随机变量X的密度函数为：

f(x;α)=α[1-Φ(x)]α-1φ(x),x∈R,α>0

(1)

其中φ(x)和Φ(x)分别是标准正态随机变量的密度函数和分布函数，α是用来控制偏度的形状参数,则称随机变量X服从参数为α的alpha正态分布，记为X～AN(α)。

当α=1时，式(1)就简化为标准正态分布；当α>1时，alpha正态分布的密度函数向右偏；当α<1时，密度函数向左偏。图1给出了α取不同值时的密度函数曲线。

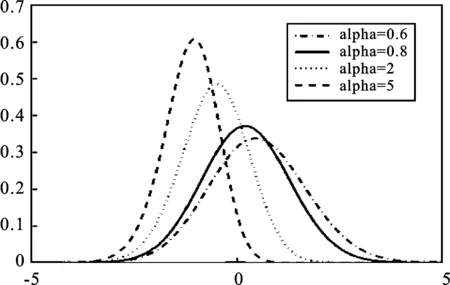
图1　α不同时alpha正态分布的概率密度函数曲线

若X～AN(α)，则其分布函数为：

F(x;α)=1-[1-Φ(x)]α,x∈R,α>0

(2)

图2给出了α取不同值时的分布函数曲线。从图2中可以看出α取值越大，分布函数曲线越陡峭。

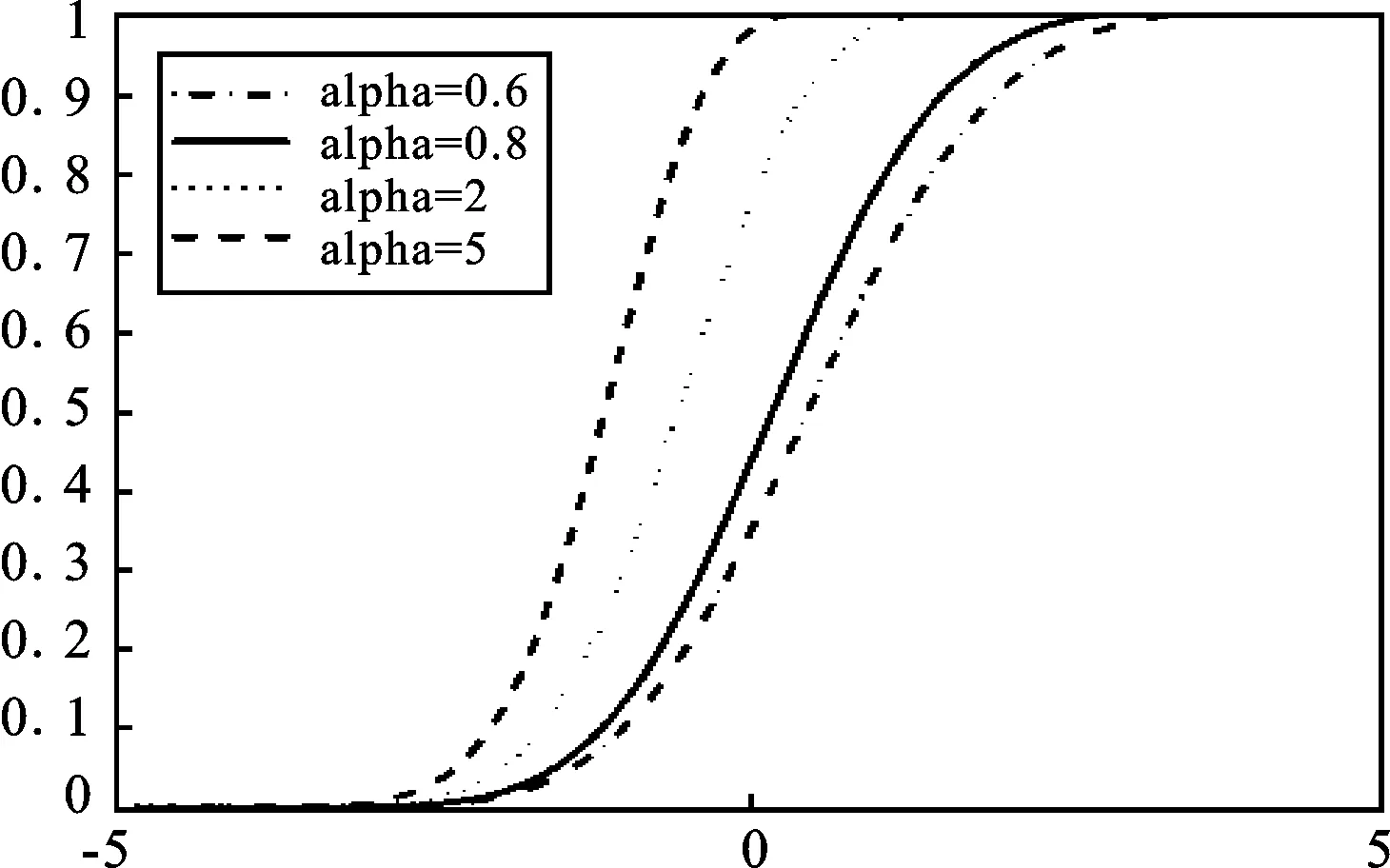
图2　α不同时alpha正态分布的分布函数曲线

三、Alpha正态分布的性质

(一)期望和方差

若随机变量X～AN(α)，则其期望为：

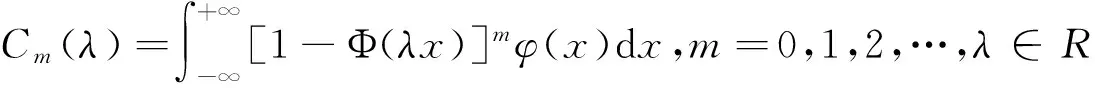
由于被积函数为奇函数[16]，所以：

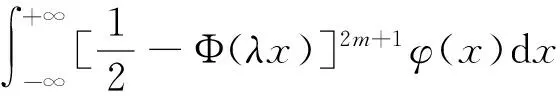
=0

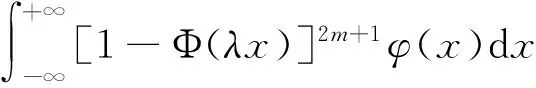
则

C2m+1(λ)

由此可得：

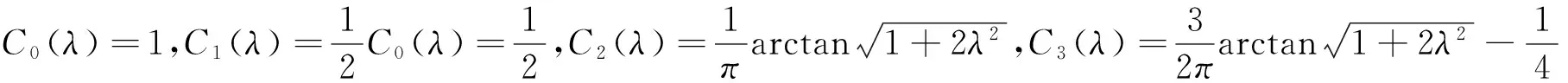
X2的矩母函数为：

MX2(t)=E(etX2)

则

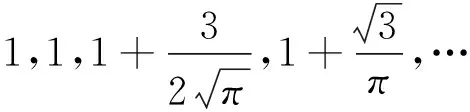
由Var(X2)=E(X2)-[E(X)]2可得方差的值。k阶中心矩为[17]：

=(k-1)E[Xk-2]+

=(k-1)E[Xk-2]+

=(k-1)E[Yk-2]+

其中U的密度函数为：

(二)随机数的生成

由上述alpha正态分布的定义，可利用反函数法产生随机数[18]485-490。首先，从[0,1]区间上生成n个均匀分布的随机数ri,i=1,2,…,n,然后令ri=1-[1-Φ(xi)]α解出。本文中取n=1 000、α=2时alpha正态分布的随机数。图3和图4分别为所抽取随机数的密度直方图和分布函数图。

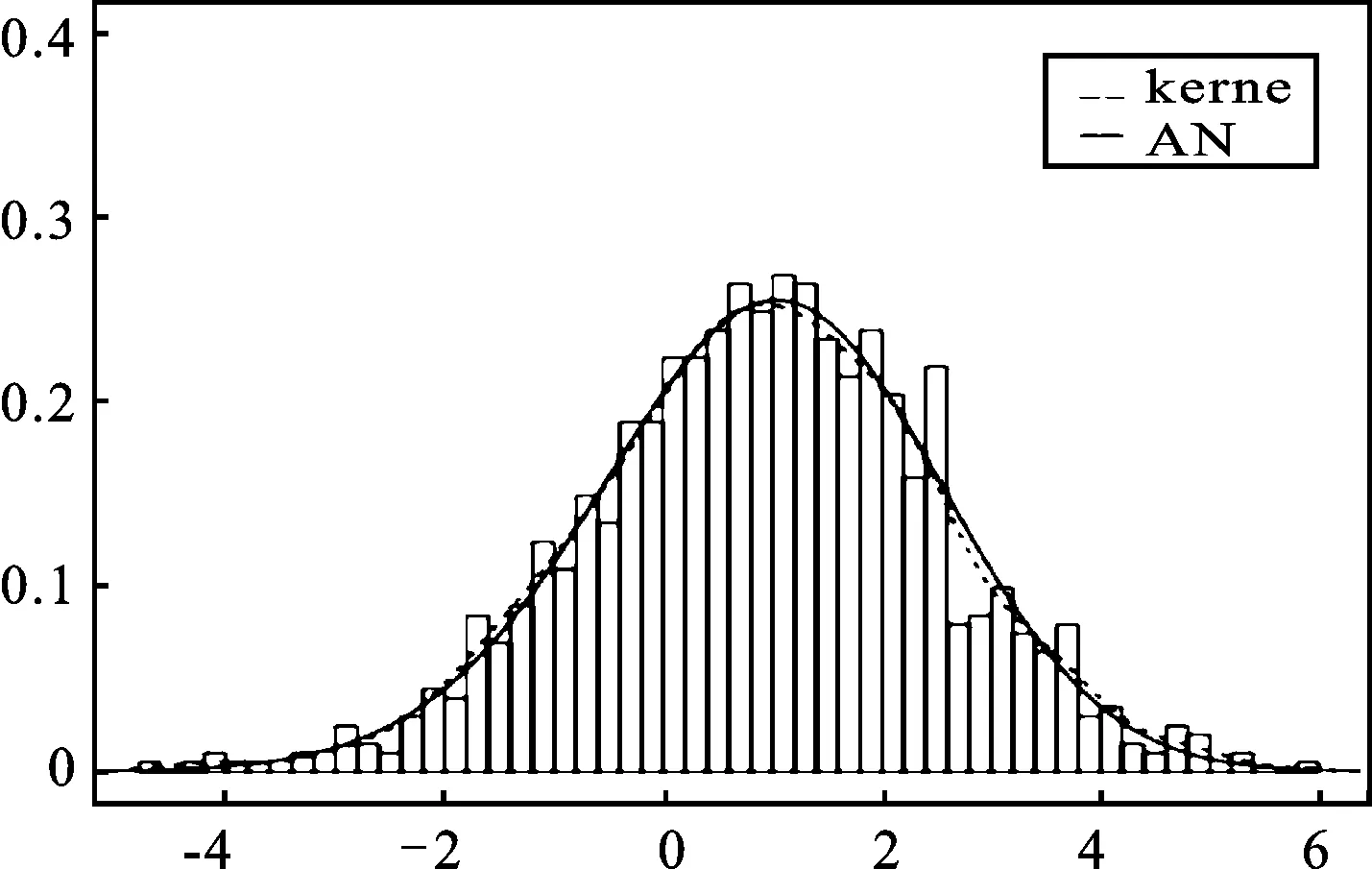
图3　生成随机数的密度直方图与alpha正态密度函数曲线图

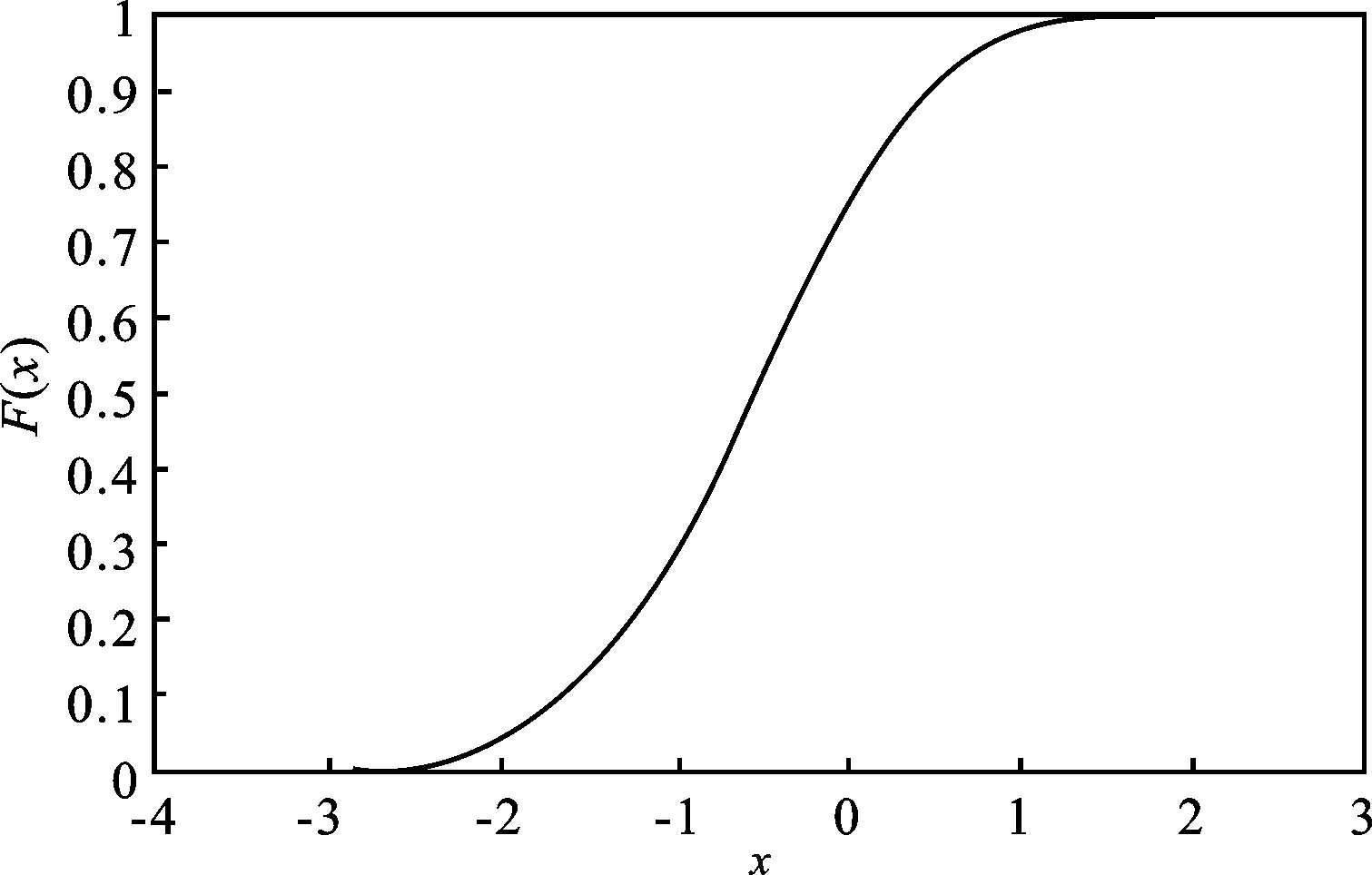
图4　生成随机数的经验分布图

从图3核密度估计曲线与alpha正态分布的密度函数曲线对比以及图4可以看出，生成的随机数是来自于alpha正态分布的。

四、极大似然估计

下面通过在密度函数中引入位置参数μ和尺度参数σ来考虑alpha正态分布的一般形式。记Y为来自alpha正态分布AN(α)的随机变量，令X=μ+σY,μ∈R,σ>0,则X的密度函数为：

f(x;μ,σ,α)

(3)

假设X1,X2,…,Xn为来自式(3)的n个随机样本，记θ=(μ,σ,α)则对数似然函数为[19]199-202：

(4)

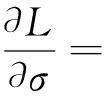
解上述方程可得：

(5)

将式(5)带入式(4)得：

利用R中L-BFGS-B方法求得上式极大值，即可得到μ、σ的估计值，进而可得α的估计值。

五、模拟学习

众所周知，极大似然估计量在一定条件下具有渐近正态性和一致性。为了说明估计的性质，从alpha正态分布中产生1 000个随机数，分别抽取30次和100次进行模拟学习，所得到的模拟结果如表1所示。

从表1可以看出，随着样本量的增加估计值逐渐趋近于真实值。

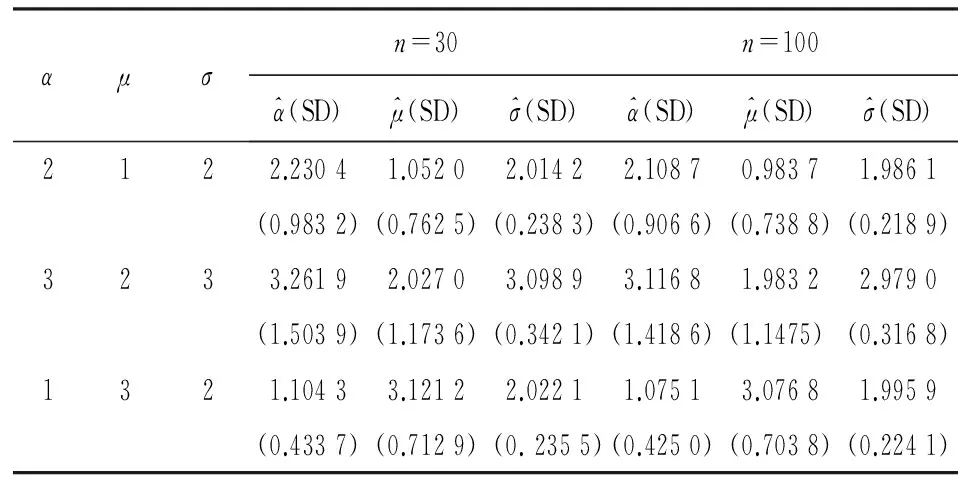
表1　不同alpha正态分布参数的经验均值和标准差

六、数据分析

本节中采用香港特别行政区2010年全年日观测一氧化氮浓度数据作为分析对象，利用alpha正态分布对所提出的数据进行建模，计算各参数的最大似然估计以及对数似然值。利用AIC准则(即AIC=-2logL+2k)和BIC准则(即BIC=-2logL+klogn)进行模型拟合，其中k是参数的个数，L是似然函数的极大值，n是样本的个数，并将alpha正态分布、偏正态与广泛应用的正态分布、对数正态分布的拟合进行比较，其相应的密度函数分别为：

计算结果如表2所示。

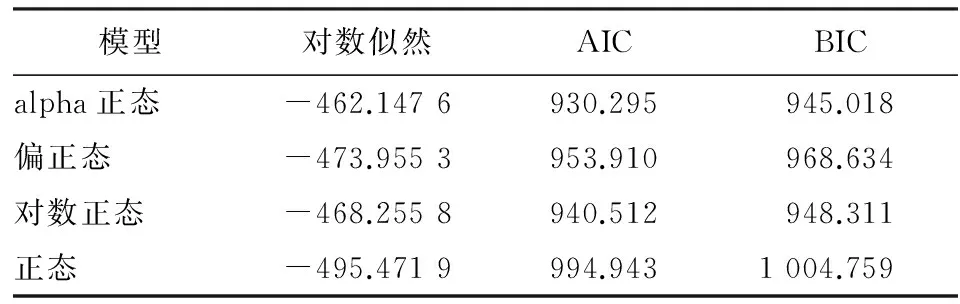
表2　正态、偏正态、对数正态及alpha正态的准则值

从表2可以看出，对于一氧化氮浓度数据集，alpha正态分布的AIC和BIC值最小，而似然函数值最大，对数正态分布与偏正态分布相差不大，而正态分布由于是对称分布则不能够捕捉到数据的有偏重尾性，这表明alpha正态分布能够有效地描述数据集的特性。

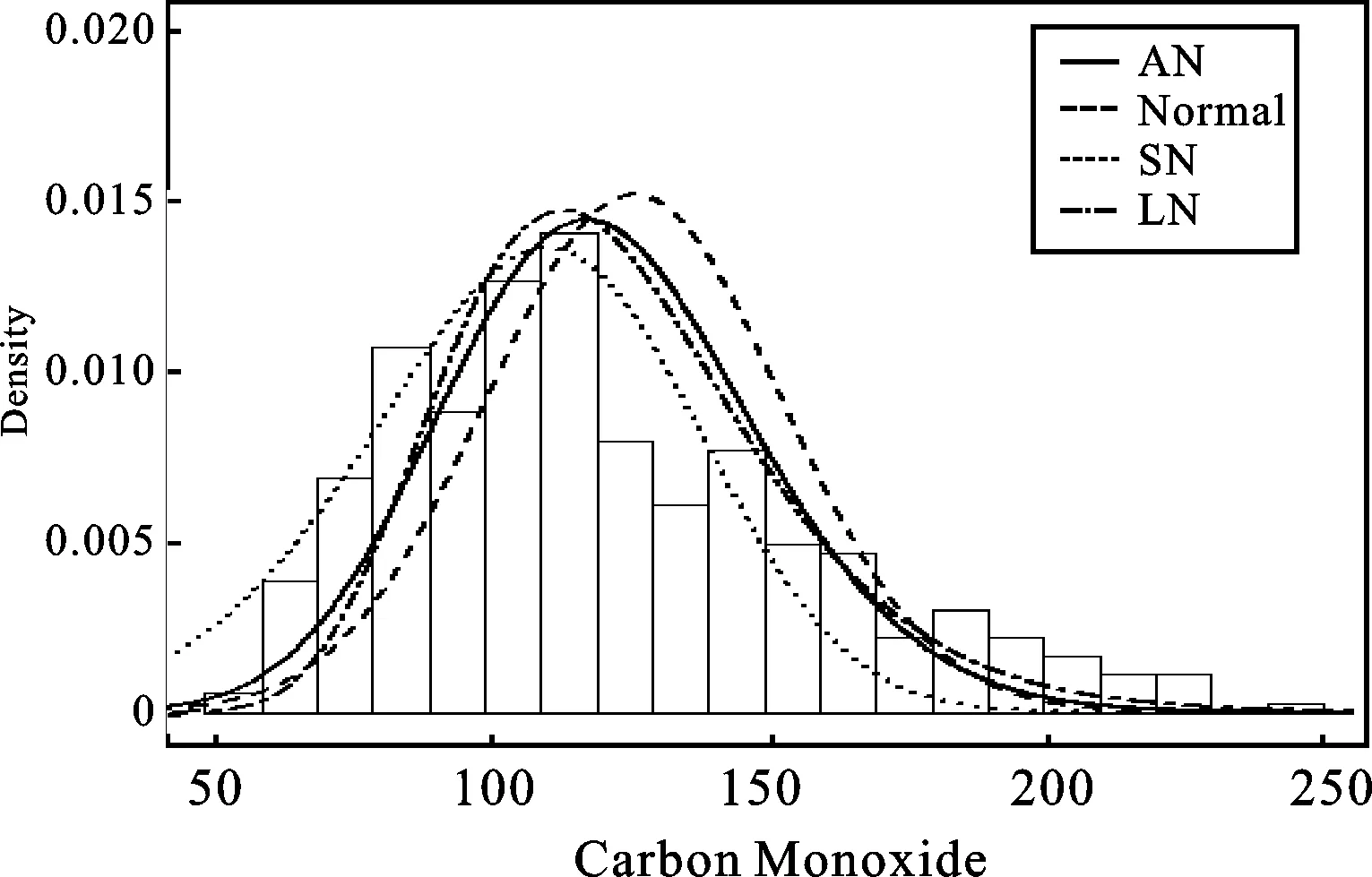
图5　一氧化氮浓度直方图及其各拟合曲线图

另外从图5中也可以看出，alpha正态分布不论是从偏度上还是峰度上都能够很好地拟合数据集，是拟合一氧化氮浓度的最佳分布；其次是所熟知的对数正态分布。对数正态分布能够较好地拟合数据的偏度，而偏正态分布尽管在处理右尾时的数据不如对数正态分布，但是在拟合数据左边的厚尾时要比对数正态分布更为适合，因此在对大气污染数据处理时也可以选择目前并没被广泛应用的偏正态分布以及本文所提出的alpha正态分布，这些分布为处理实际生活中的有偏重尾数据提供了很好的模型。

下来考虑对于给定的数据集，正态分布和alpha正态分布有无显著性差异，其对应的假设为：

H0:α=1,即样本来自正态分布

H1:α≠1,即样本来自alpha正态分布

七、结 论

本文介绍了一个包含正态分布作为特殊情形的新分布族——alpha正态分布，并研究了它的基本性质、随机数的生成以及参数的极大似然估计方法，且从其密度函数曲线可以看出alpha正态分布可以是左偏、右偏或者对称的，此种新的有偏分布相比偏正态分布以及目前在污染物浓度数据集中被广泛应用的对数正态分布，在处理有偏和重尾数据上有着更大的灵活性，因此可用此分布来拟合非对称数据集。 本文中通过拟合空气污染物浓度数据，并利用统计判别准则将其与偏正态分布、正态分布及对数正态分布进行比较，得出所提分布对此数据集提供了一个更好的拟合，这为我们处理现实生活中的非对称数据集提供了一个新的统计模型。

参考文献：

[1]范绍佳. 城市大气污染物浓度分布研究[J]. 中山大学学报论丛，1993,12(1).

[2]韩婧,代志光，李文韬. 西安市灰霾天气下PM2.5浓度与气象条件分析[J]. 环境污染与防治, 2014, 36(2).

[3]陈静. 榆林市空气污染物浓度统计特征及其气象影响研究[D]. 西安：长安大学硕士学位论文, 2015.

[4]Wayne R Ott. A Physical Explanation of the Lognormality of Pollutant Concentrations[J]. Air and Waste Manage. Assoc., 1990,40(10).

[5]Larry G Blackwood. The Lognormal Distribution, Environmental Data and Radiological Monitoring[J]. Environmental Monitoring and Assessment,1992, 21(3).

[6]Lu Hsin-Chung. The Statistical Characters of PM10 Concentration in Taiwan Area[J]. Atmospheric Environment, 2002, 36(3).

[7]Kan Haidong, Bingheng Chen. Statistical Distributions of Ambient Air Pollutants in Shanghai, China [J]. Biomedical and Environmental Sciences, 2004, 17(3).

[8]Ahrens L H. The Log-normal Distribution of the Elements[J]. Geochimica Et Cosmochimica Acta, 1954, 6(2).

[9]Azzalini A. A Class of Distributions Which Includes the Normal Ones[J]. Scand. J. of Statist.,1985, 12(2).

[10]Henze N. A Probabilistic Representation of the Skew-normal Distribution [J]. Scand. J. Statist., 1986, 13(4).

[11]Azzalini A, Dalla Valle A. The Multivariate Skew-normal Distribution [J]. Biometrika,1996, 83(4).

[12]Azzalini A, Capitanio A. Statistical Applications of the Multivariate Skewed Normal Distribution [J]. Journal of Royal Statistical Society, 1999, 61(3).

[13]Huang W J, Chen Y H. Generalized Skew Cauchy Distribution [J]. Statist. Probab. Lett.,2007, 77(11).

[14]陈明明，马江洪，杨楠. 关于斜Laplace分布与Levy偏稳定分布的性质[J]. 统计与信息论坛，2014, 29(7).

[15]Gupta R D, Gupta R C. Analyzing Skewed Data by Power Normal Model[J]. Test, 2008, 17(1).

[16]Arnold B C, Beaver R J. Skewed Multivariate Models Related to Hidden Truncation and Selective Reporting[J]. Test, 2002, 11(11).

[17]Gupta R C, Gupta R D. Generalized Skew Normal Model[J]. Test, 2004,13(2).

[18]薛毅，陈立萍. R统计建模与R软件[M]. 北京：清华大学出版社，2007.

[19]茆诗松，程依明，濮晓龙. 概率论与数理统计教程[M].北京：高等教育出版社，2004.

(责任编辑：崔国平)

The Alpha Normal Distribution and Its Application to Environmental Pollution

CHEN Ming-minga, MA Jiang-hongb, JI Nan-nanb

(a. School of Economics and Management; b. College of Science, Chang'an University, Xi'an 710064, China)

Abstract:In the present, some symmetric distributions are often used to deal with real data, such as normal and t distribution. However, the results given by these symmetric distributions are not very satisfactory. Skew distributions are commonly used to handle with skew and heavy-tailed data, based on the classical normal distribution, we propose a new model, called alpha normal distribution, to deal with such data, develop its parametric estimation methods and several basic properties. Applying the proposed distribution to environmental pollution data, through the test shows that the alpha normal distribution gives good results.

Key words:skew distribution; alpha normal distribution; maximum likelihood estimation; environmental pollution

收稿日期：2015-12-31

基金项目：国家自然科学基金项目《基于信息瓶颈编码原理的深度学习研究》(11501049)；国家自然科学基金项目《模糊假设的统计检验理论和方法研究》(11261044)

作者简介：陈明明，女，山东枣庄人，博士生，研究方向：运输统计分析。

中图分类号：O212.1∶F205

文献标志码：A

文章编号：1007-3116(2016)06-0022-06

马江洪，男，陕西绥德人，教授，理学博士，研究方向：数据挖掘的统计学方法。

姬楠楠，女，陕西渭南人，讲师，理学博士，研究方向：深度学习。

【统计理论与方法】